Similar presentations:
Нахождение и использование регрессионных зависимостей
1. Нахождение и использование регрессионных зависимостей
Графеева Н.Г.2016
2. Регрессия (в статистике)
• Одна из задач Data Mining – нахождение регрессионных зависимостей.• Регрессия (regressio — обратное движение) в статистике — статистическая зависимость
среднего значения случайной величины от значений другой случайной величины или
нескольких случайных величин; введена Фрэнсисом Гальтоном (1886).
В отличие от чистой функциональной зависимости y = f(x) , которая каждому значению
независимой переменной x ставит в соответствие одно определённое значение
величины y , при регрессионной зависимости одному и тому же значению x могут
соответствовать различные значения величины y. Если при каждом значении x = xi
наблюдается n значений yi1, yi2, …, yin величины y , то зависимость среднего
арифметического
yi' = (yi1 + yi2 +…+ yin)/n
• от xi и является средней регрессией.
• Классическим примером средней регрессии служит зависимость среднего роста детей
от роста родителей, а также зависимость средних диаметров сосен от их высот и т.п.
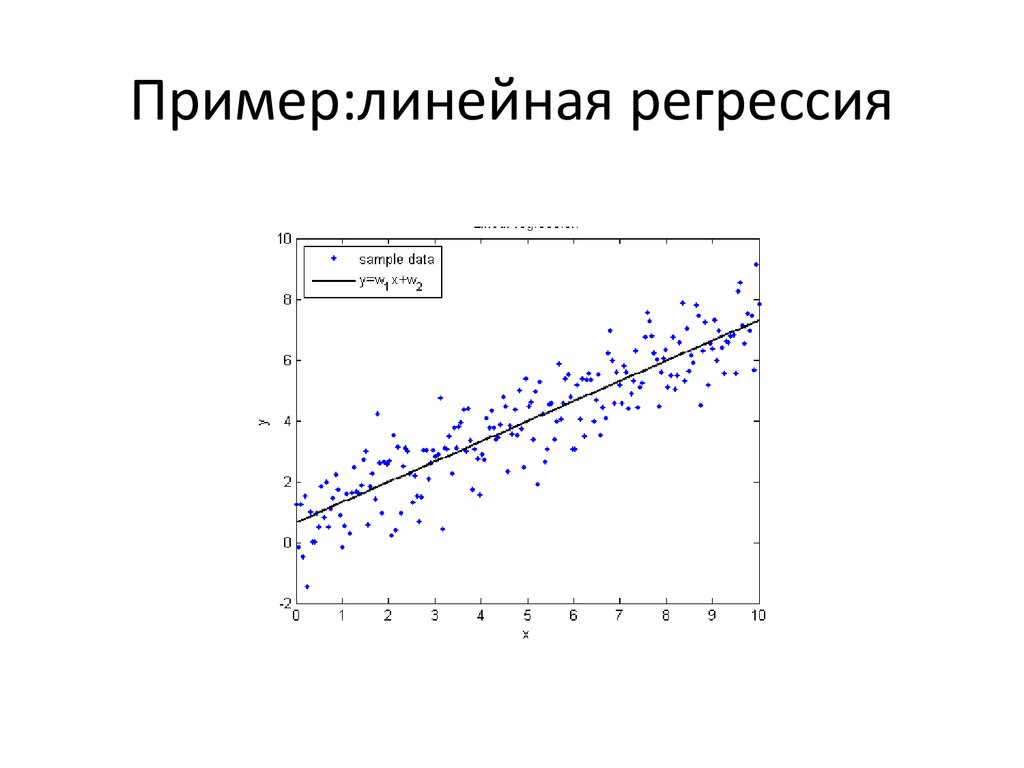
3. Пример:линейная регрессия
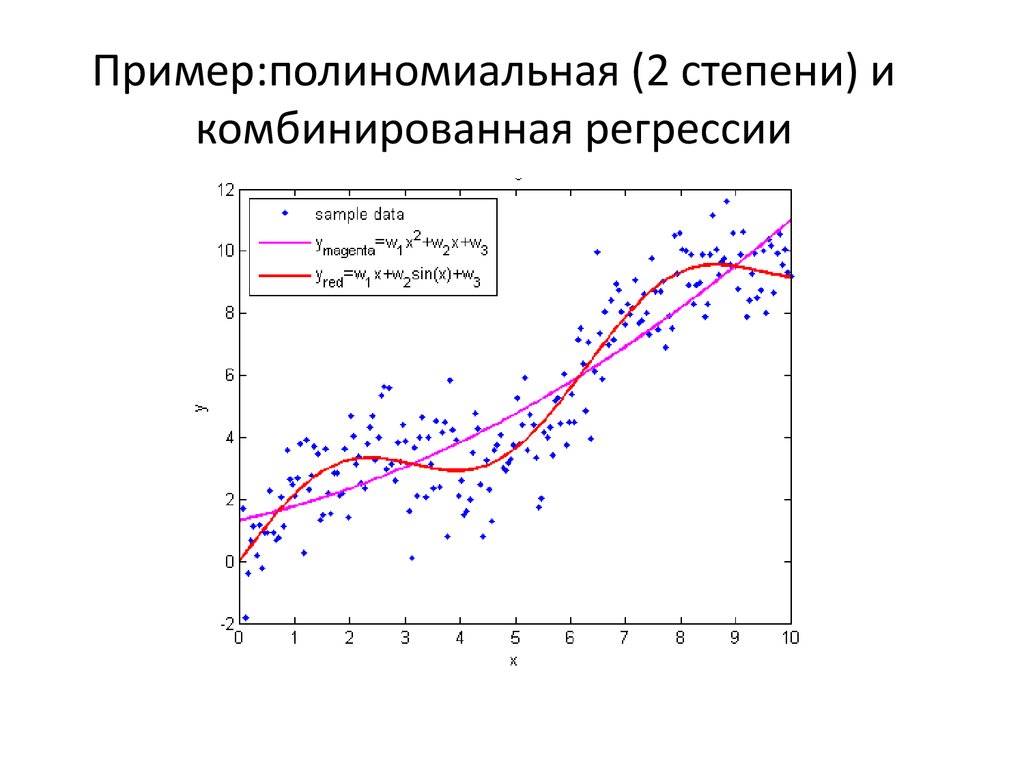
4. Пример:полиномиальная (2 степени) и комбинированная регрессии
5. Для каких задач могут использоваться регрессионные зависимости?
• Восстановление пропущенных значений вданных;
• Сглаживание зашумленных данных;
• Прогнозирование;
• Определение трендов в зашумленных данных;
• Оценивание качества торговых стратегий
биржевых роботов
• и т.п.
6. Какие бывают регрессии?
Линейные
Полиномиальные
Синусоидальные
Экспоненциальные и т.п.
• Сегодня рассмотрим только метод
определения линейной регрессии и оценку
качества …
7. Как определить линейную регрессию?
Любая линейная функция может быть записана уравнением:y=ax+b
• Задача заключается в отыскании коэффициента a и смещения
b таких, чтобы все исследуемые точки лежали наиболее
близко
к
линии
регрессии.
С этой целью чаще всего используется метод наименьших
квадратов (МНК), суть которого заключается в следующем:
сумма квадратов отклонений значения точки от линии
регрессии принимает минимальное значение.
8. Метод наименьших квадратов
9. Пример: прямая, построенная по методу наименьших квадратов
10. Метод наименьших квадратов
Определениекоэффициентов
уравнения y = ax + b:
11. Применение линейной регрессии для прогнозов и сглаживания
• Можно применять линейную регрессию для прогнозирования (сглаживания)значений в пределах наблюдаемого диапазона возможных значений.
• Мы предсказываем среднюю величину y для наблюдаемых x, которые имеют
определенное значение путем подстановки этого значения в уравнение
линейной
регрессии.
• Итак, если x = x0 ,прогнозируем (сглаживаем) y как
y0 = a* x0 + b
• Примечания: в задачах линейного сглаживания и прогнозирования вовсе не
требуется опираться на весь исторический период наблюдений.
Наоборот, следует использовать только последнюю, наиболее значимую
часть наблюдений!
12. Как оценить качество прогноза?
• Можно использовать одну из возможныхметрик, например MAPE (Mean Absolute
Percentage Error ):
• где n-количество предсказаний,
• yt - реальное значение,
• Ft – предсказанное значение.
13. Как оценить качество линейной регрессии?
• В некоторых прикладных задачах мы должны строитьлинейную регрессию на основе всех точек наблюдения и
оценивать ее качество (например, оценка эффективности
работы биржевого робота). Для такой оценки существует
понятие коэффициента детерминации – R 2. Он может
принимать значения от 0 до 1. Основной смысл этого
понятия – если анализируемые точки лежат близко к линии
регрессии, то линия хорошо соответствует исходным
данным. Если коэффициент детерминации близок к 1,
линия соответствует исходным данным, близок к 0 – плохо
(то есть исходная кривая неустойчивая и плохо
аппроксимируется прямой линией).
14. Как рассчитывается коэффициент детерминации?
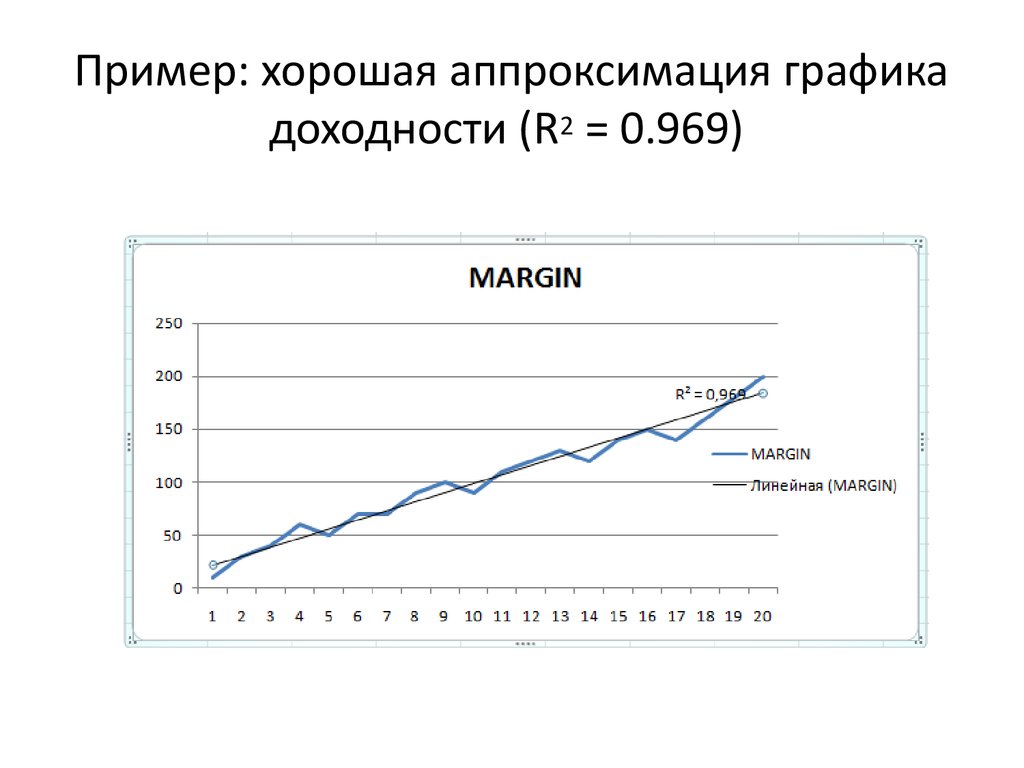
15. Пример: хорошая аппроксимация графика доходности (R2 = 0.969)
16. Пример: плохая аппроксимация графика доходности (R2 = 0.012)
17. Есть ли какие-нибудь подходящие функции в современных СУБД?
• Все наиболее известные СУБД на сегодняшнийдень тянутся к внедрению разнообразных
методов data mining (особенно в последних
релизах). Разумеется, ORACLE тоже. В частности
в качестве метода линейной регрессии в нем
реализован метод наименьших квадратов,
позволяющий вычислять коэффициент a и
смещение b для соответствующего линейного
уравнения y = ax + b.
18. Как выглядят соответствующие функции в ORACLE SQL?
REGR_COUNT(y, x) –количество пар в sql-запросе сопределенными значениями для y и x (т.е. не null)
REGR_SLOPE(y, x) - коэффициент a для линейного
уравнения y=ax+b
REGR_INTERCEPT (y, x) - смещение b для линейного
уравнения y=ax+b
REGR_R2(y,x) – коэффициент детерминации
Примечание: в sql функциях regr_slope и regr_intercept
реализован метод наименьших квадратов.
19. Использование функций регрессии в ORACLE SQL
select regr_slope(2 * id + 5, id) "КОЭФФИЦИЕНТ A",regr_intercept(2 * id + 5, id) "СМЕЩЕНИЕ B"
from goodsamount


















 database
database








