Построение и анализ алгоритмов. Динамическое программирование. Аналогии. (Лекция 4.3)

1. Построение и анализ алгоритмов

Лекция 4.3
Динамическое программирование
АНАЛОГИИ
16.02.2016
Динамическое
программирование
1

2. АНАЛОГИИ

Решение методом динамического программирования
Задачи:
Перемножение цепочки матриц
Оптимальные БДП
Задача Х и т.п.
Задачи подсчёт а и задачи опт имизации.
Например:
«Число различных расстановок скобок» и
«Оптимальная расстановка»
16.02.2016
Динамическое
программирование
2

3. Оценка количества узлов дерева

Из лекции про
перемножение
матриц
Оценить количество узлов дерева в общем случае можно
подсчётом всех возможных вариантов расстановок
скобок в произведении матриц.
Пусть pn – число вариантов расстановок скобок в
произведении n сомножителей (включая самые внешние
скобки).
Например, для трёх сомножителей abc имеем два варианта
(a(bc)) и ((ab)c), а следовательно, p3 = 2.
В общем случае, считая, что «последнее» по порядку
умножение может оказаться на любом из n –1 мест, запишем
следующее рекуррентное соотношение:
pn = p1 pn –1 + p2 pn –2 + … + pn –2 p2 + p n –1 p1.
16.02.2016
Динамическое
программирование
3

4.

Из лекции про
Начальное условие p1 = 1. Далее
перемножение
матриц
p2 = p1 p1 = 1,
p3 = p1 p2 + p2 p1 = 2,
p4 = p1 p3 + p2 p2 + p3 p1 = 5.
Оказывается [7, с. 393], что решением этого рекуррентного
уравнения являются так называемые числа Каталана
pn = Сn –1, где Сn =(2 k | k) / (k +1),
а запись (n | m) обозначает биномиальный коэффициент
(n | m) = n!/(m! (n – m)!).
При больших значениях n справедливо
Cn 4
n
n πn
т. е. число узлов в дереве перебора есть экспоненциальная функция от n.
16.02.2016
Динамическое
программирование
4

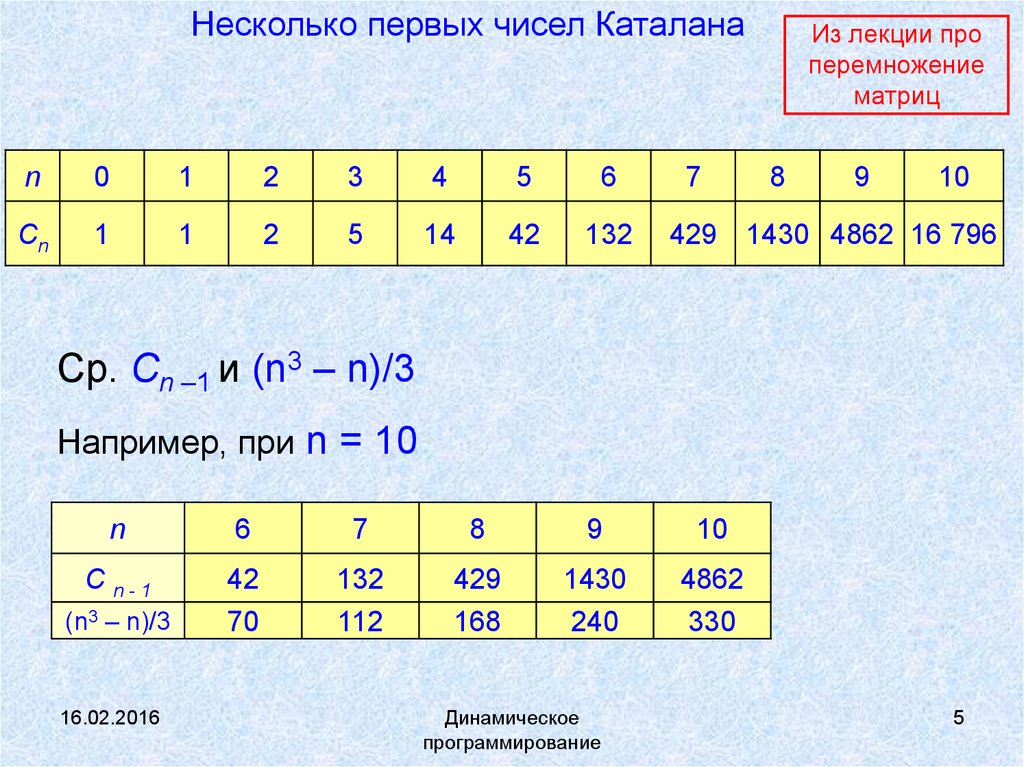
5.

Несколько первых чисел Каталана
n
0
1
2
3
4
5
6
7
Cn
1
1
2
5
14
42
132
429
Из лекции про
перемножение
матриц
8
9
10
1430 4862 16 796
Ср. Сn –1 и (n3 – n)/3
Например, при n = 10
n
6
7
8
9
10
C n-1
42
70
132
112
429
168
1430
240
4862
330
(n3 – n)/3
16.02.2016
Динамическое
программирование
5

6.

Число bn структурно различных бинарных деревьев с n узлами
n 1
bn bk bn k 1 b0bn 1 b1bn 2 ... bn 2b1 bn 1b0 ,
k 0
1
b0 1, b1 1.
Из лекции
про БДП
k 0..(n – 1)
bk
bn k 1
Это рекуррентное уравнение с точностью до обозначений совпадает с
рекуррентным уравнением, получающимся при подсчёте числа
расстановок скобок в произведении n сомножителей
(см. лекцию 16, слайд 16).
16.02.2016
Динамическое
программирование
6

7.

Из лекции
b2 = b0 b1 + b1 b0 = 2,
про БДП
b3 = b0 b2 + b1 b1 + b2 b0 = 5,
b4 = b0 b3 + b1 b2 + b2 b1 + b3 b0 =
= 5 + 2 + 2 + 5 = 14
Решением рекуррентного уравнения являются так
называемые числа Каталана Сn, т. е. bn = Сn.
Ранее были приведены общая формула для чисел
Каталана и асимптотическое соотношение
n
4
Cn
n πn
n
0
1
2
3
4
5
6
7
Cn
1
1
2
5
14
42
132
429
16.02.2016
Динамическое
программирование
8
9
10
1430 4862 16 796
7

8. Решение методом динамического программирования

1. Структура оптимального решения
2. Рекуррентное соотношение
3. Вычисление оптимальной стоимости (по
рекуррентному соотношению)
4. Построение оптимального решения
Проиллюстрировать на предыдущих примерах
16.02.2016
Динамическое
программирование
8

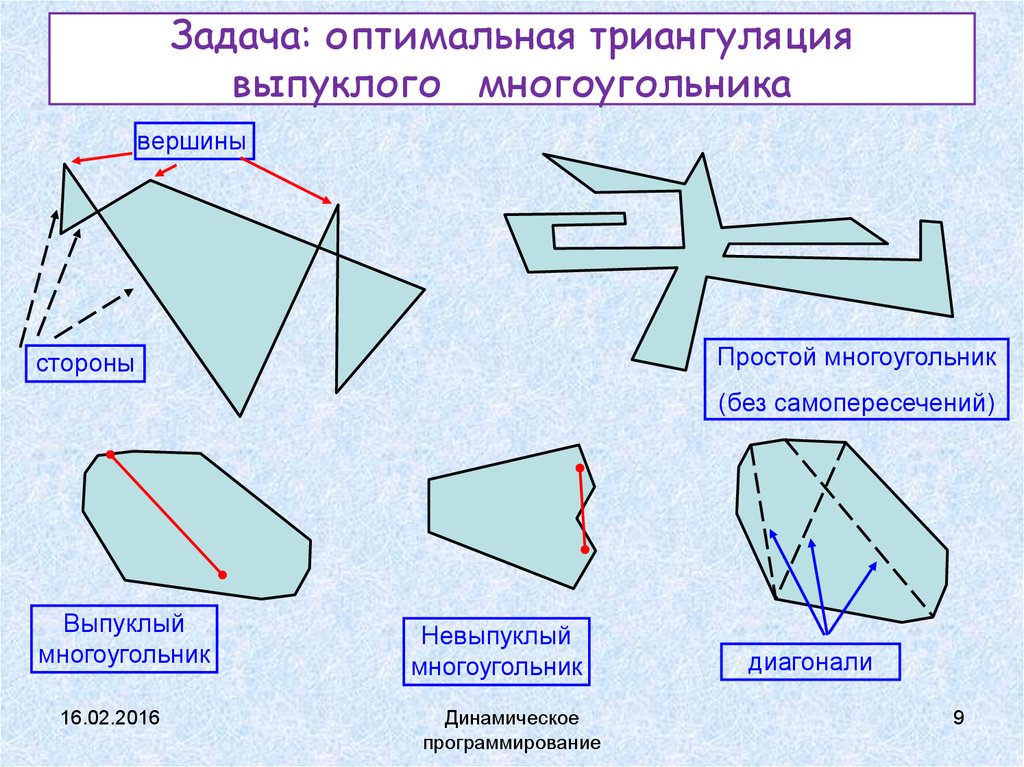
9. Задача: оптимальная триангуляция выпуклого многоугольника

вершины
Простой многоугольник
стороны
(без самопересечений)
Выпуклый
многоугольник
16.02.2016
Невыпуклый
многоугольник
Динамическое
программирование
диагонали
9

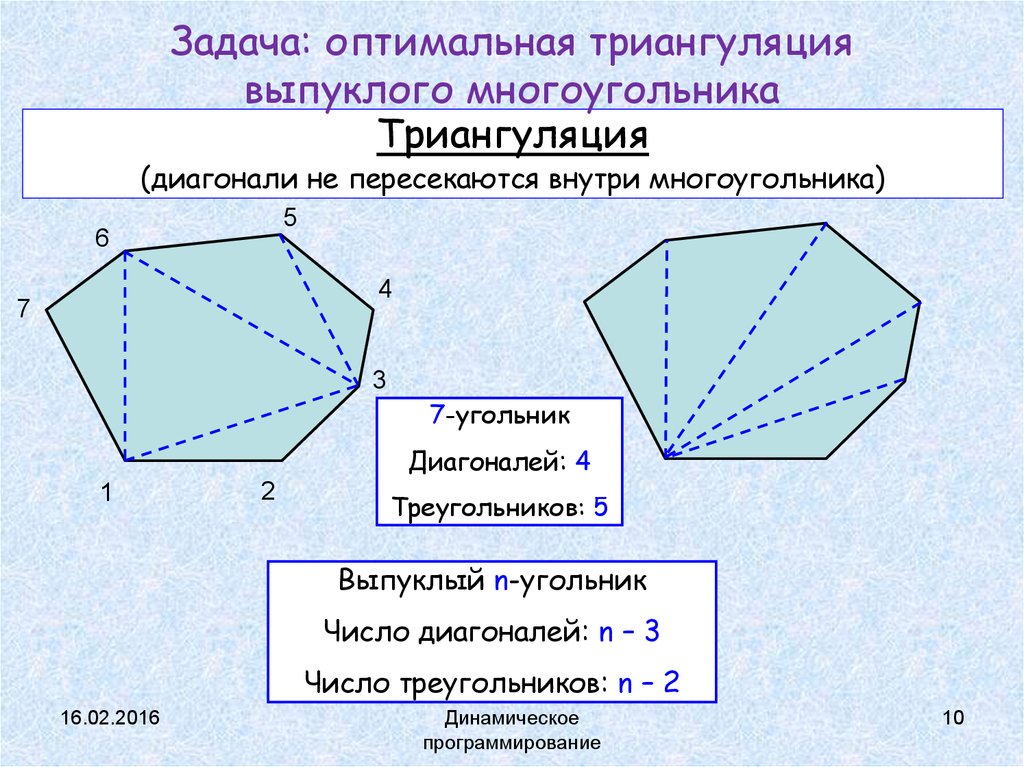
10. Задача: оптимальная триангуляция выпуклого многоугольника

Триангуляция
(диагонали не пересекаются внутри многоугольника)
5
6
4
7
3
7-угольник
Диагоналей: 4
1
2
Треугольников: 5
Выпуклый n-угольник
Число диагоналей: n – 3
Число треугольников: n – 2
16.02.2016
Динамическое
программирование
10

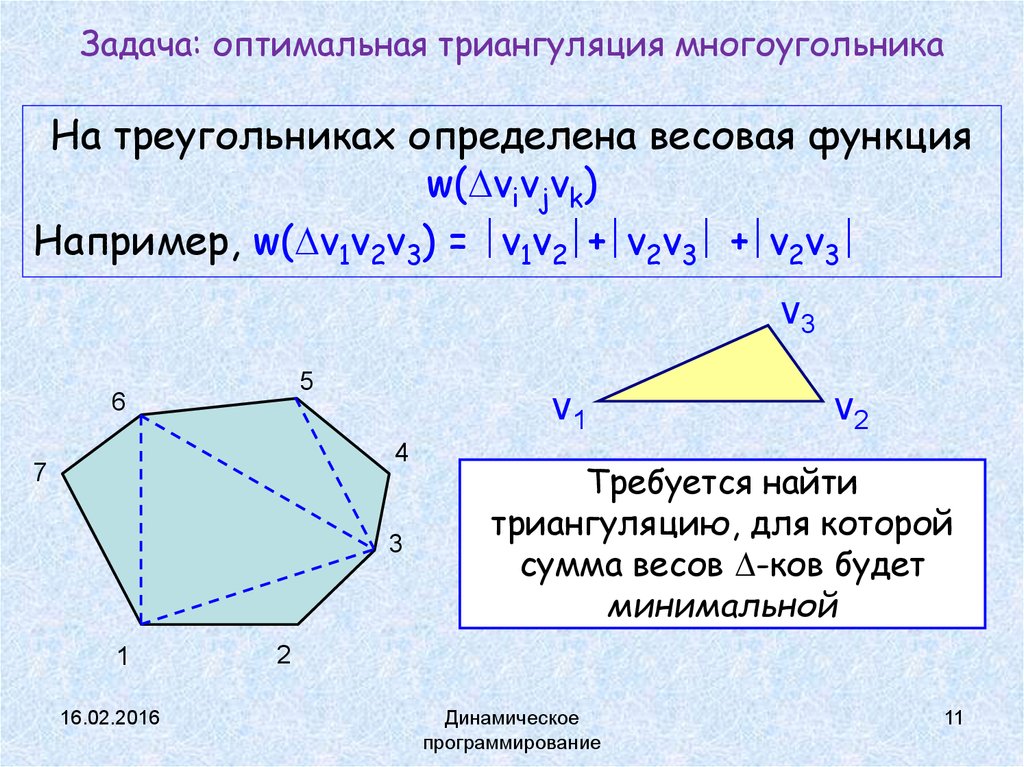
11. Задача: оптимальная триангуляция многоугольника

На треугольниках определена весовая функция
w( vivjvk)
Например, w( v1v2v3) = v1v2 + v2v3 + v2v3
v3
5
6
v1
4
7
3
1
16.02.2016
v2
Требуется найти
триангуляцию, для которой
сумма весов -ков будет
минимальной
2
Динамическое
программирование
11

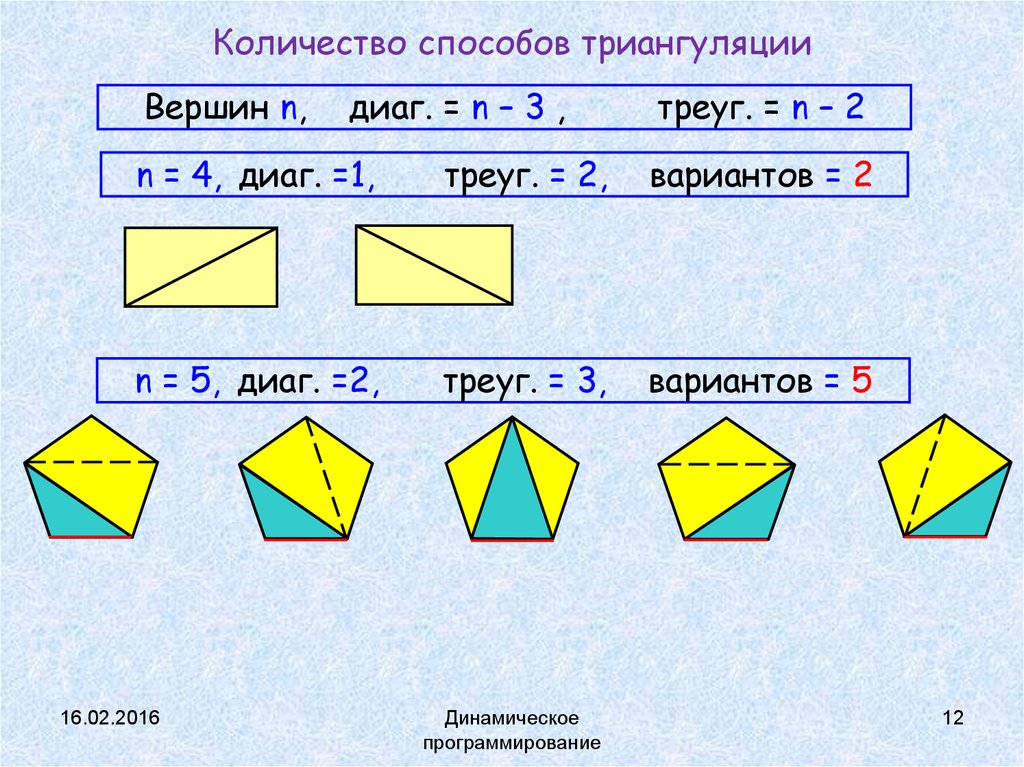
12. Количество способов триангуляции

Вершин n,
диаг. = n – 3 ,
треуг. = n – 2
n = 4, диаг. =1,
треуг. = 2,
вариантов = 2
n = 5, диаг. =2,
треуг. = 3,
вариантов = 5
16.02.2016
Динамическое
программирование
12

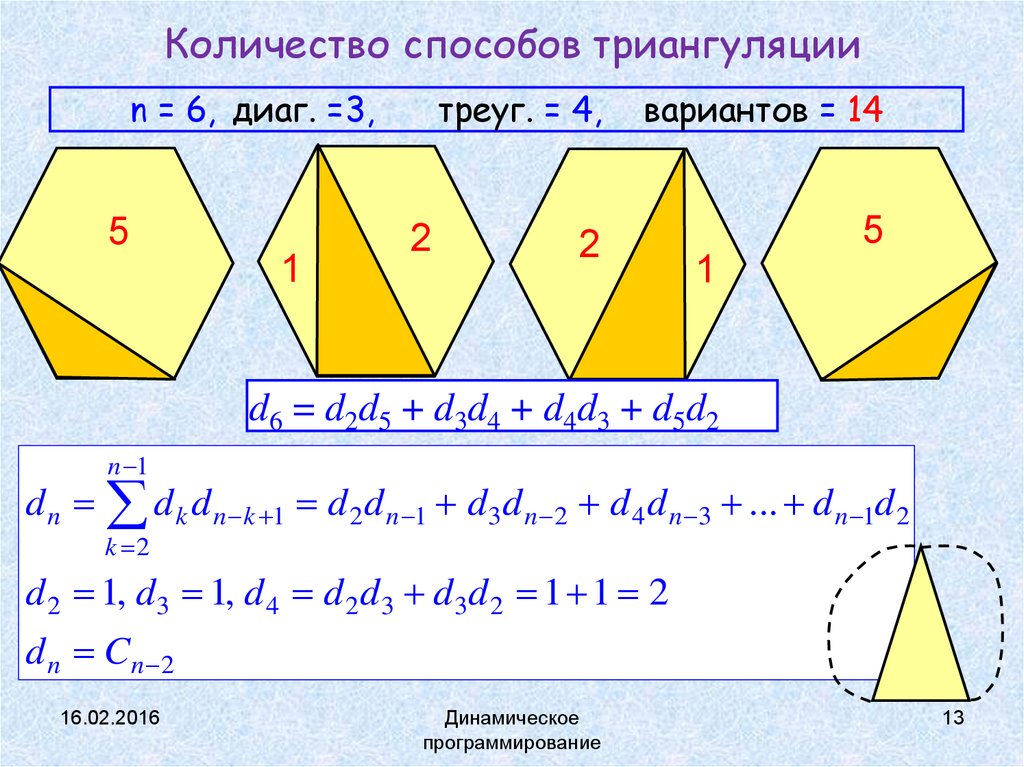
13. Количество способов триангуляции

n = 6, диаг. =3,
5
1
2
треуг. = 4,
вариантов = 14
2
5
1
d6 = d2d5 + d3d4 + d4d3 + d5d2
n 1
d n d k d n k 1 d 2 d n 1 d3d n 2 d 4 d n 3 ... d n 1d 2
k 2
d 2 1, d3 1, d 4 d 2 d3 d3d 2 1 1 2
d n Cn 2
16.02.2016
Динамическое
программирование
13

14. Рекуррентная формула для веса оптимальной триангуляции многоугольника (ОТМ), 1

Mij = многоугольник (vi, vi+1,…, vj), i<j, т.е. (j-i+1)-угольник
Т.е. M1n = многоугольник (v1, v2,…, vn)
mij min {mik mkj w(vi vk v j )}, i 1 j ,
i k j
mi ,i 1 0
mij – вес ОТМ (vi,vi+1,…,vj)
vk
m1n – вес ОТМ (v1,v2,…,vn)
Для двуугольника mi,i+1 = w(vi-1,vi)=0
vi
16.02.2016
Динамическое
программирование
vj
14

15. Динамическое программирование

Вычисление таблиц:
mi,i+1 = 0,
mi,i+2 = w( i,i+1,i+2),
mi,i+3 =…
…
mi,i+n-2 m1,n-1 , m2,n
mi,i+n-1 = m1n
{при i=1..n-1}
{при i=1..n-2}
{при i=1, 2}
{при i=1}
Время С1n3, память С2n2
16.02.2016
Динамическое
программирование
15

16. Рекуррентная формула для веса оптимальной триангуляции многоугольника (ОТМ), 2

Mij = многоугольник (vi-1, vi,…, vj), i<j, т.е. (j-i+2)-угольник
Т.е. M1n = многоугольник (v0, v2,…, vn), т.е. это (n+1)-углнк
mij min {mik mk 1, j w(vi 1vk v j )}, i j ,
i k j
В таком виде почти
полное сходство с
прежними примерами!
mii 0
mij – вес ОТМ (vi-1,vi,…,vj)
vk
m1n – вес ОТМ (v0,v1,…,vn)
Для двуугольника mii = w(vi-1,vi)=0
Время С1n3, память С2n2
16.02.2016
Динамическое
программирование
vi-1
vj
16

17. Упражнения

1.
2.
3.
Доказать, что триангуляция n–угольника содержит
n-2 треугольника и n-3 диагоналей.
Пусть вес треугольника = его площади. Можно ли
упростить алгоритм поиска ОТМ?
Весовая функция определена на множестве
диагоналей многоугольника. ОТМ — сумма весов
диагоналей минимальна. Как свести эту задачу к
рассмотренной?
Задание. Рассмотрите полностью какой-либо
пример с 5- или 6-угольниками.
(для тренировки к ТК)
16.02.2016
Динамическое
программирование
17

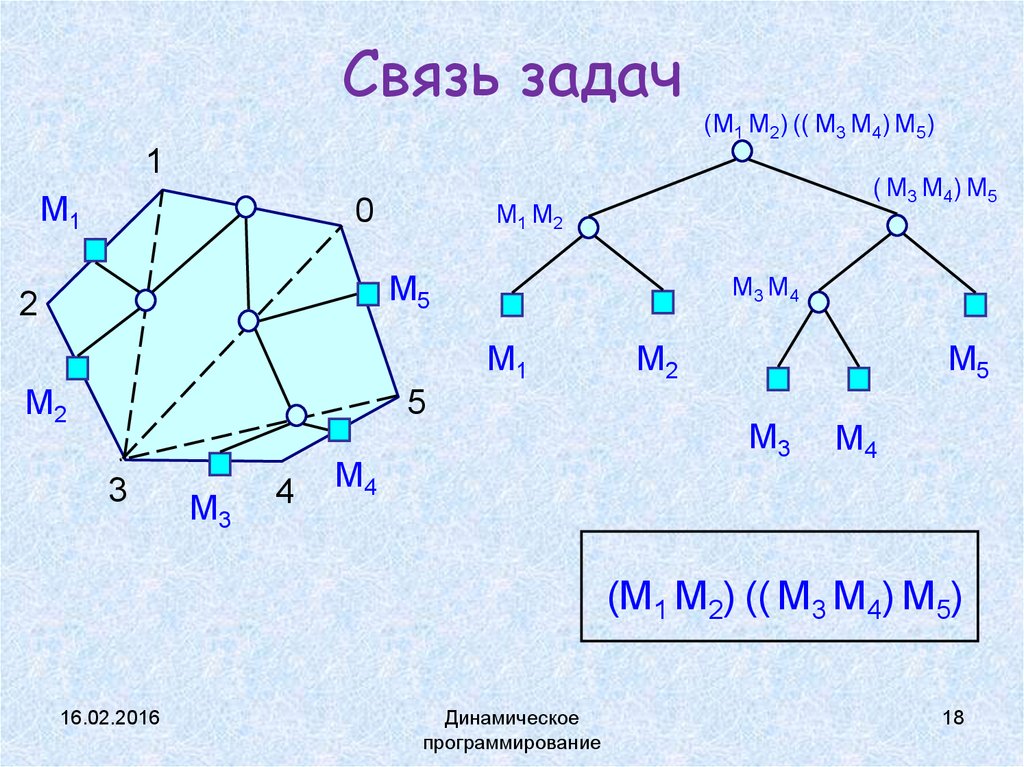
18. Связь задач

(M1 M2) (( M3 M4) M5)
1
M1
0
( M3 M4) M5
M1 M2
M5
2
M 3 M4
M1
M2
M2
M5
5
M3
3
M3
4
M4
M4
(M1 M2) (( M3 M4) M5)
16.02.2016
Динамическое
программирование
18

19. Связь задач

1
(M1 M2) (( M3 M4) M5)
M1
0
M5
M1 M2
2
(M1 M2) (( M3 M4) M5)
( M3 M4 ) M5
M2
5
M3 M 4
3
16.02.2016
M3
4
M4
w( vivjvk) = ri rj rk
Динамическое
программирование
19

20.

Деревья
Триангуляции
16.02.2016
Динамическое
программирование
20

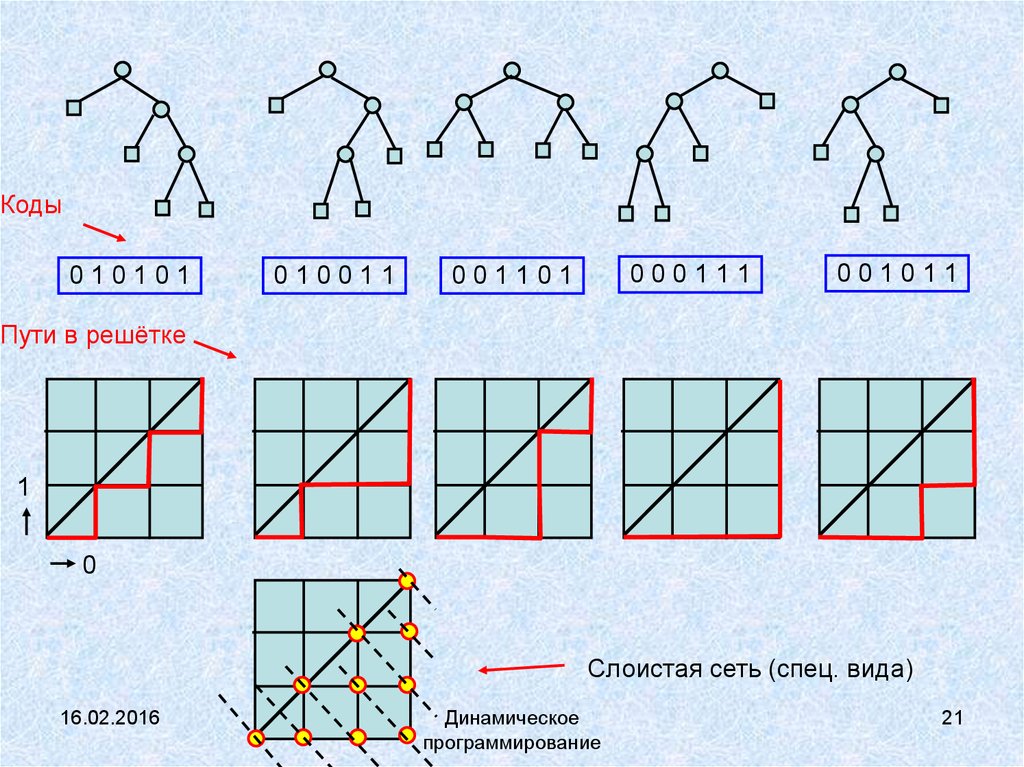
21.

Коды
010101
010011
000111
001101
001011
Пути в решётке
1
0
Слоистая сеть (спец. вида)
16.02.2016
Динамическое
программирование
21

22. Преобразование «Ползущий червь»

Обход в глубину:
от узла влево – 0; вправо - 1
010011
16.02.2016
Динамическое
программирование
22

23. Литература

1. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы:
построение и анализ : учеб./ М.: МЦМНО, 1999. – 960 с.
(Классические учебники: Computer science). (Доп. тираж
2000 г., 2001 г., 2002 г.) [Опт.Трианг.]
2. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К.
Алгоритмы: построение и анализ, 2-е издание.: Пер. с
англ. – М.: Издательский дом «Вильямс», 2007, 2009. –
1296 с.
3. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К.
Алгоритмы: построение и анализ, 3-е издание.: Пер. с
англ. – М.: ООО «И.Д. Вильямс», 2013. – 1328 с.
16.02.2016
Динамическое
программирование
23

24.

КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
16.02.2016
Динамическое
программирование
24