Моделирование социально-экономических процессов

1.

ФГОУ ДПО «Институт дополнительного
профессионального образования»
Моделирование социально-экономических
процессов
Поленин В.И.
E-mail: [email protected]

2.

Основа и место в учебном плане
Раздел 9
Основы экономической безопасности РФ
Концептуальные основы моделирования систем и процессов управления.
Оценка эффективности управления социально-экономическими системами.
В результате изучения этой главы должны:
знать:
понятия «метод», «модель» , «методика»;
понятия «эффективность», «показатель» и «критерий» эффективности;
виды моделей и моделирования, их современное состояние и характеристики;
возможности и ограничения моделирования социально-экономических систем;
основы и примеры моделирования социально-экономических систем;
уметь:
формулировать такие понятия, как «метод», «модель» , «методика»,
«эффективность», «показатель» и «критерий» эффективности;
различать типы социально-экономических моделей по основным признакам
классификации;
владеть:
пониманием возможностей моделирования социально-экономических процессов;
общими понятиями математического моделирования социально-экономических
процессов.
2

3.

3
Понятия «метод», «способ», «методика», «методология»
МЕТОД (от греч . methodos - путь исследования, теория, учение),
способ достижения какой-либо цели, решения конкретной
теоретической задачи; совокупность приемов или операций, которые
нацелены на решение определённой задачи теоретического освоения
(познания) действительности.
Примеры: метод алгебраических преобразований, метод наименьших
квадратов, логико-вероятностный метод, экспертный метод,
статистический метод, метод нечетких множеств, метод теории игр.
СПОСОБ – порядок, образ действий, метод в исполнении какой-либо
цели, решения конкретной практической задачи.
МЕТОДИКА – некий готовый «рецепт», алгоритм, процедура для
проведения каких-либо нацеленных действий. Как правило, порядок
действий, расчета для получения результата при заданных исходных
данных.
МЕТОДОЛОГИЯ – общий подход к выбору методов решения задач того
или иного класса.

4.

Понятия «задачи решаются», «задачи выполняются»4
Решаются теоретические, научные, учебные, математические
задачи.
Задачи практической деятельности выполняются.

5.

Математическое моделирование
5
Невозможно представить себе современную науку без широкого
применения математического моделирования.
Сущность этой методологии состоит в замене исходного объекта его
«образом» — математической моделью — и дальнейшем изучении модели с
помощью реализуемых на компьютерах вычислительно-логических алгоритмов.
Этот «третий метод» познания, конструирования, проектирования сочетает
в себе многие достоинства как теории, так и эксперимента.
Работа не с самим объектом (явлением, процессом), а с его моделью дает
возможность безболезненно, относительно быстро и без существенных
затрат исследовать его свойства и поведение в любых мыслимых ситуациях
(преимущества теории).
В то же время вычислительные (компьютерные, имитационные)
эксперименты с моделями объектов позволяют, опираясь на мощь современных
вычислительных методов и технических инструментов информатики, подробно
и глубоко изучать объекты в достаточной полноте, недоступной чисто
теоретическим подходам (преимущества эксперимента).

6.

Методы, модели, методики
Технические, экологические, социальные, экономические и иные
системы, изучаемые современной наукой, не поддаются исследованию (в
нужной полноте и точности) обычными теоретическими методами.
Прямой натурный эксперимент над ними долог, дорог, часто либо
опасен, либо попросту невозможен, так как многие из этих систем
существуют в «единственном экземпляре».
Цена ошибок и просчетов в обращении с ними недопустимо высока.
Поэтому математическое (шире — информационное) моделирование
является неизбежной составляющей научно-технического прогресса.
Сама постановка вопроса о математическом моделировании какоголибо объекта порождает четкий план действий. Его можно условно
разбить на три этапа: модель — алгоритм — программа.
6

7.

Методы, модели, методики
Создав триаду «модель—алгоритм—программа», исследователь
получает в руки универсальный, гибкий и недорогой инструмент,
который вначале отлаживается, тестируется в «пробных»
вычислительных экспериментах.
После того как адекватность (достаточное соответствие) триады
исходному объекту удостоверена, с моделью проводятся
разнообразные и подробные «опыты», дающие все требуемые
качественные и количественные свойства и характеристики объекта.
Будучи методологией, математическое моделирование не
подменяет собой математику, физику, биологию и другие научные
дисциплины, не конкурирует с ними. Его роль – синтезирующая.
Моделирование присутствует почти во всех видах творческой
активности людей различных «специальностей» — исследователей и
предпринимателей, политиков и военачальников.
7

8.

О соотношении целей, задач и критериев.
Варианты постановки задачи принятия решения
8
• Цель − желаемое будущее состояние, желаемая будущая
обстановка, желаемый конечный результат деятельности.
• Задача − формулировка цели в форме заданных действий
по ее достижению.
• Говорят, что цели достигаются выполнением задач.
• Удачное определение задачи: «деятельностная
формулировка цели».
• Таким образом, если цель − желаемое будущее, то задача
− действия по ее достижению.

9.

О соотношении целей, задач и критериев.
Варианты постановки задачи принятия решения
Лицо, принимающее решение (ЛПР):
• с помощью аппарата, персонала поддержки его
деятельности, содержательно анализирует
поставленную перед ним задачу как проблему и
формирует варианты действий по универсальной
системе деятельностных категорий: кто, что, где,
когда и как;
• осуществляет выбор наилучшего варианта с
помощью критерия или системы критериев, заданных
старшим руководителем в постановке задачи или
выдвинутых самим ЛПР.
9

10.

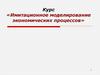
Понятия «показатель» и «критерий»
Показатель −
шкала
со стрелкой
Критерий −
красная или
зеленая отметка
на шкале
10

11.

Основные общие черты уникального выбора при
решении социально-экономических задач:
- уникальность, неповторяемость ситуации;
- нехватка и недостоверность части информации;
- наличие разнородных факторов влияния;
- трудности определения полного списка
вариантов;
- сложный для оценки, многоаспектный характер
вариантов;
- субъективный характер многих оценок качества
вариантов;
- недостаточная определенность последствий
того или иного варианта решения, выбора.
11

12.

Пример инженерно-технической задачи
Однокритериальная (скалярная) задача
принятия решений
12

13.

Задачи принятия решений в социальноэкономических системах:
13
1. Охватывают большое количество параметров
(многопараметрические задачи).
2. Связаны с поиском решения не с одним критерием
(скалярного решения), а векторного решения с
максимизацией или минимизацией сразу нескольких
показателей.
3. Связаны с учетом качественных факторов.
4. Связаны с учетом случайных факторов:
- стохастических (вероятностных, статистических)
факторов;
- неопределенных факторов.
5. Связаны с учетом коллективных мнений экспертов.
Следствие: модели и задачи относятся к категории
слабо структурированных и плохо формализуемых систем .

14.

Теория и практика принятия решений
Нобелевский лауреат в области экономики Маурицио Элайс :
«Остается только сожалеть о вторжении математиков,
которые больше интересуются развитием чисто
математических моделей, чем анализом их отношений с
реальным миром...
Печально, что никому не нужные математические
упражнения ценятся больше, чем подходящие методики анализа
фактов.
Таковыми являются основы теории вероятностей
Колмогорова и теория игр Неймана—Моргенштерна, которые
представляют собой два блестящих примера из многих».
14

15.

Обобщенная постановка задачи в социальноэкономической области
Выбор наилучшего, наиболее предпочтительного варианта
(способа, альтернативы) х* из множества возможных вариантов
осуществляется по критериальному правилу,
принципу оптимальности Ф, отражающему попарное сравнение
вариантов
,
и систему предпочтений ЛПР
( лучше, предпочтительнее, чем
)
*
{ X }, Ф х
Х x1 ,..., x n
хi : х j
хi х j
х хj
i, j 1,..., n
j 1,..., n
15

16.

Вариант постановки задачи принятия решения с указа- 16
нием формализованного критерия оптимальности
Выбор наилучшего, наиболее предпочтительного варианта
(альтернативы) х* из множества возможных вариантов
осуществляется по формализованному критериальному правилу Ф Р:
наилучшему варианту х* соответствует экстремум Р* (по смыслу задачи
максимальное или минимальное значение) показателя качества или
эффективности Р.
{ X }, ФР х
*
ФР : Р extrx* x ,..., x Р
1
n

17.

Случай множественного (векторного) критерия
оптимальности
Многокритериальная (здесь – двухкритериальная),
векторная задача принятия решений
(пример выбора одного из 9 автомобилей по двум
показателям)
Эффективное множество по Парето
17

18.

Определение понятия «модель»
18
Модель – это упрощенное подобие реального объекта, явления,
процесса:
– макет;
– схема, изображение или описание явления или процесса;
– физический аналог объекта (игрушка, испытательный
маломасштабный образец), функционирование которого по
определённым параметрам подобно функционированию
реального объекта;
– информационный аналог объекта (математическая,
программная, алгоритмическая модель), функционирование
которого по определённым параметрам подобно
функционированию реального объекта.

19.

Назначение моделирования и моделей
19
Аспектами моделирования могут быть внешний вид, структура, поведение
объекта, а также все их возможные комбинации.
Внешний вид, поведение объекта интуитивно понятны.
Моделирование внешнего вида используется для:
– идентификации (узнавания) объекта (штрих-код, дактилоскопия);
– долговременного хранения образа (фото, чертежи).
Структурой объекта называют совокупность его элементов, а также существующих
между ними связей.
Моделирование структуры объекта используется для:
– наглядного представления (структура атома кислорода, молекулы воды,
производства, правительства);
– изучения свойств объекта (слабые, ненадежные элементы, требующие
дублирования, ролевая значимость элементов).
Моделирование поведения применяется при:
– планировании, прогнозировании (экономика определенного типа);
– выявления причинно-следственных связей (прогноз погоды);
– управлении (станки с ЧПУ, транспорт, производство);
– конструировании технических устройств (шасси автомобиля).

20.

Свойства моделей
В процессе моделирования каждый аспект моделирования
раскрывается через совокупность свойств, которые оцениваются,
анализируются.
В моделях отражаются не все свойства, это и не нужно, а только
существенные с точки зрения целей моделирования. Чем меньше
попадает в модель ненужных свойств, тем полезнее модель.
Бритва ОО́ккама –
методологический принцип «Не
следует множить , привлекать
новые сущности без надобности,
без крайней на то необходимости».
Свойства:
– качественные (дальний-ближний, быстро-медленно, горячийхолодный);
– количественные – параметры модели.
20

21.

Информационные модели
21
Основной тип моделей в науке – информационные модели – описания
моделируемых объектов и процессов на одном из языков кодирования
информации программирования, информационных технологий.
Входы
x1
x1
…
F(x)
Y1
Y1
Выходы
…
xn
Ym
В информационных
моделях свойства, имеющие количественную
природу, выражаются значениями функции отклика (Yi).
Виды информационных моделей:
Описательные (дескриптивные) – применяются для описания свойств
и параметров процесса принятия решений в целях прогнозирования его
хода в будущем: на естественном языке, словесное описание, на
специальном языке, математические формулы, алгоритмы, программы,
таблицы, графы, деревья, сети, блок-схемы, карты.
Нормативные (прескриптивные) – применяются для принятия
решений, для оптимизации процессов.

22.

Виды моделей – некоторые примеры
22
Прогностические – моделью изменения температуры на улице будет являться
график, на котором будет показано изменение температуры с течением
времени на будущее.
Имитационные.
Оптимизационные.
Неформализованные (качественное описание) – формализованные
(математические, компьютерные).
Статические – динамические.
Детерминированные – стохастические (вероятностные).

23.

Средства и системы моделирования
23
Пакет MATLAB
Современный самый мощный пакет прикладных программ .
Создатель и правообладатель – фирма "The Math Works Inc" (USA).
Система MATLAB (сокращение от англ. «Matrix Laboratory») предназначена
для выполнения инженерных и научных расчетов и высококачественной
визуализации получаемых результатов.
Применяется практически в любой области науки и техники, в математике,
вычислительном эксперименте, имитационном моделировании, финансовых
расчетах, при математическом моделировании гидро-. аэродинамики,
акустики, энергетики и т. д.
Отличительной особенностью MATLAB является матричное представление
данных.
Ядро интегрированной системы MATLAB позволяет назвать программу
MATLAB симфонией алгоритмов.
MATLAB содержит ряд профессиональных инструментальных приложений
(toolboxes), т.е. наборы инструментов для создания, анализа и оптимизации
различных систем в таких областях, как управление, обработка сигналов,
идентификация систем и многих др.
Освоив и применяя в MATLAB тулбоксы, можно достичь уровня
разработчиков (исследователей) мирового класса.

24.

Средства и системы моделирования
24
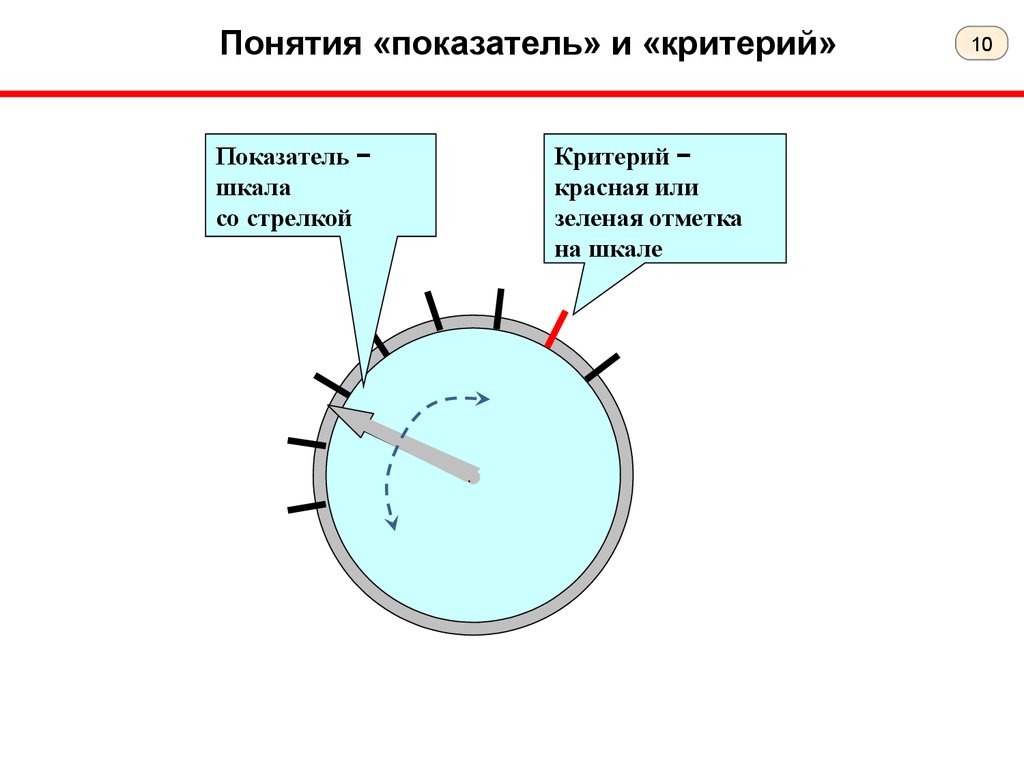
Пакет MATLAB – фрагмент программы и результатов
Белый ш ум (0;0.5)
2
30
1
20
0
10
-1
-2
0
50
100
0
-2
-1
0
1
Доля положительных значений
Выведена круговая диаграмма
доли неотрицательных значений
53%
47%
реализации белого ш ума N(0,0.5)
2

25.

Средства и системы моделирования
25
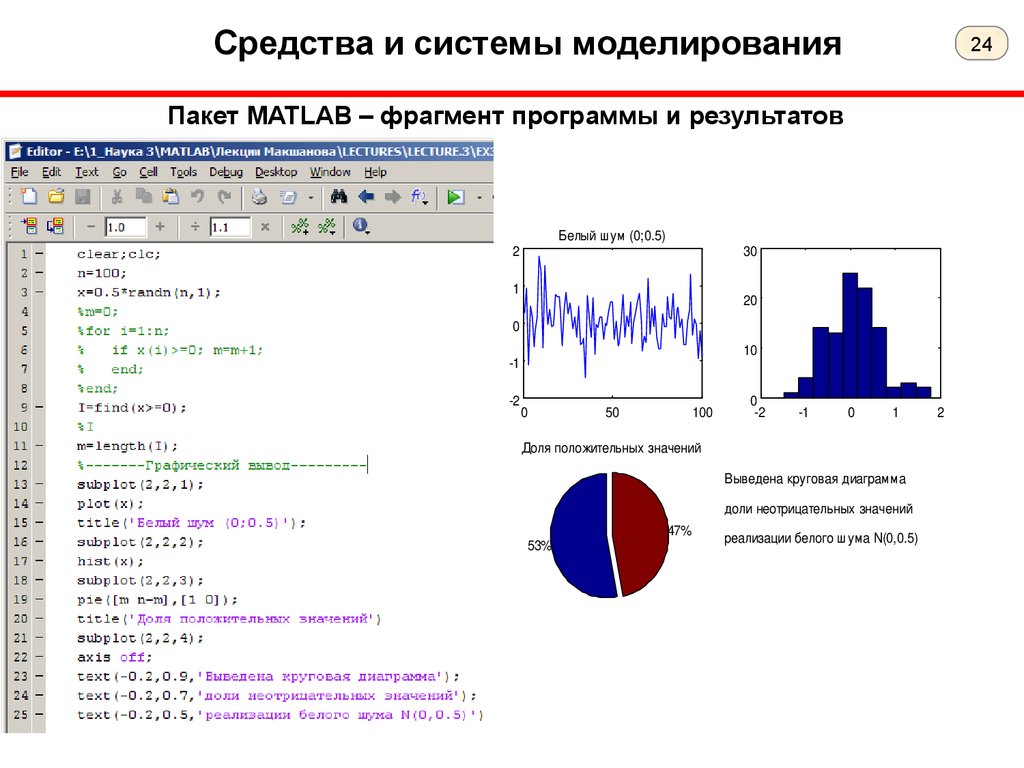
Пакет MATLAB – примеры результатов
Метод Рунге-Кутта 4 порядка
500
Теоретическое реш ение
Результат расчета
450
400
0.8
350
0.6
300
Функция у
1
0.4
0.2
250
200
150
0
1
0.5
0
-0.5
-1
-2
-1
0
1
2
100
50
0
1
1.5
2
2.5
Аргумент х
3
3.5

26.

Средства и системы моделирования
26
Пакет Mathcad
Другая сторона развития программного обеспечения ориентирована на
"непрограммирующего пользователя".
Создатель и правообладатель – фирма "The Math Works Inc" (USA).
Mathcad – универсальный математический пакет, предназначенный для
выполнения инженерных и научных расчетов.
Замечательное свойство и основное преимущество пакета перед типичными
языками программирования : операторы вычислений записываются
привычным, естественным языком математики.
В чем-то напоминает калькулятор. От калькулятора пакет Mathcad отличает
работа с различными типами данных (комплексные, векторы, матрицы),
использование библиотеки математических функций.
Пакет Mathcad относится к интегрированным пакетам, т.е. позволяет не
только произвести вычисления, но и получить итоговый отчет с
комментариями, формулами, таблицами и графиками.

27.

Пакет Mathcad – палитры инструментов
27

28.

Пакет Mathcad – пример вычислений
28

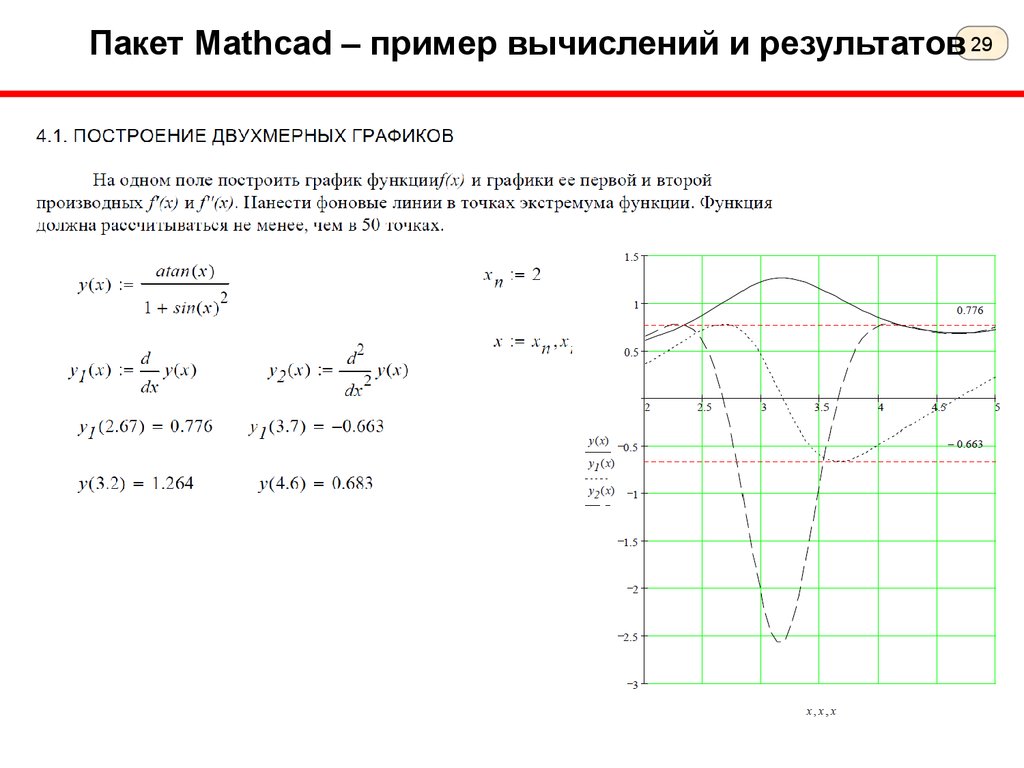
29.

Пакет Mathcad – пример вычислений и результатов 29

30.

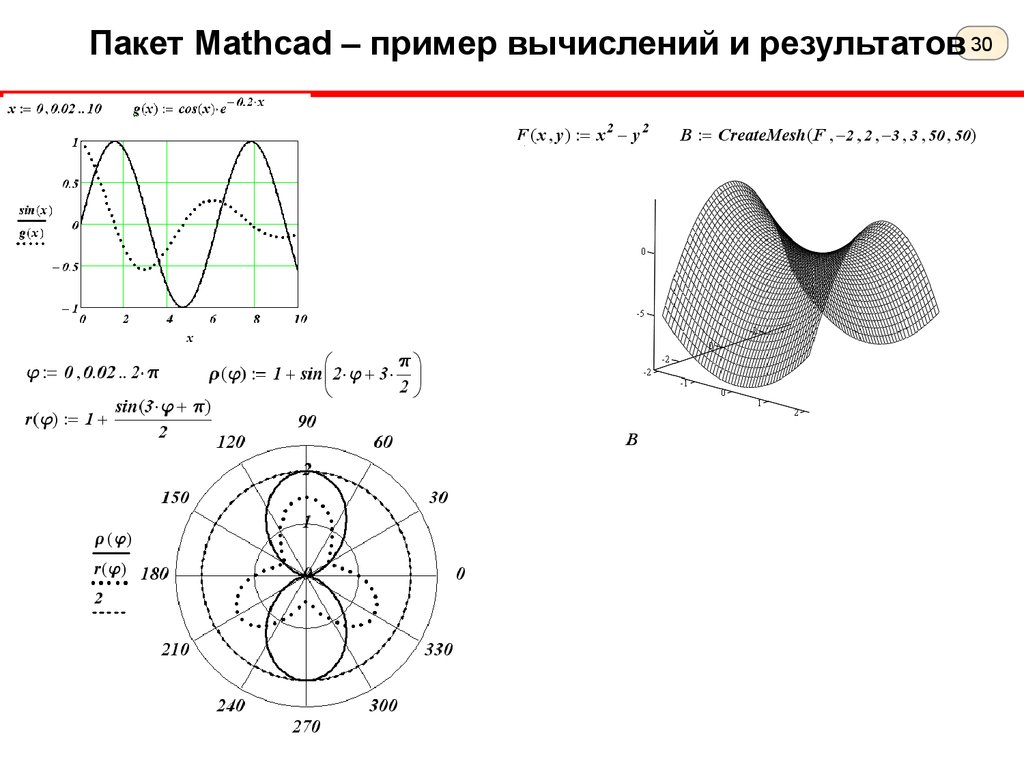
Пакет Mathcad – пример вычислений и результатов 30

31.

Средства и системы моделирования
31
AnyLogic — программное обеспечение для
имитационного моделирования сложных систем
и процессов.
Разработчик и правообладатель – российская компания «Экс Джей
Текнолоджис» (англ. XJ Technologies), зарегистрированная за рубежом как
XJ Technologies Company Ltd North America
Руководитель Андрей Борщëв,.
AnyLogicТМ -- инструмент имитационного моделирования нового поколения.
Основными строительными блоками модели являются активные объекты –
виртуальные модели объектов реального мира.
Используются технологии объектно-ориентированного моделирования:
наследование, полиморфизм и т.д.
Наследование – позволяет значительно упростить процесс разработки
моделей. Например, создав базовый объект-класс – автомобиль, можно легко
моделировать различные подклассы автомобилей (спортивные, грузовики и т.п.).
Основные характеристики будут унаследованы от базового объекта-класса, а
особенные будут заданы в подклассах.
Полиморфизм – способность системы программирования автоматически
различать общее и различное.

32.

Средства и системы моделирования
32
– система имитационного моделирования (ИМ)
Области применения:
– экономика и производство (логистика, цепочки поставок, сфера услуг,
потребительский рынок, управление активами и проектами);
– социальная сфера (демографические процессы, здравоохранение и т.п.).
Есть два рынка, связанных с системами моделирования:
– рынок самих инструментов ИМ, которые выставляются на продажу
вендорами (создателями и правообладателями);
– рынок – консалтинг, когда вендоры оказывают консультационные услуги
клиенту с целью оптимизировать его бизнес.
Консалтинговые услуги очень дорогие: один проект с применением ИМ для
крупного металлургического комбината в настоящее время выполняется за 2 млн
долларов. Сами инструменты ИМ стоят намного дешевле: AnyLogic осенью 2015
г. стоил около 4 (для ВУЗов) – 10 (для фирм) тыс.$.
AnyLogic устойчиво занимает самое высокое место на рынке технологий ИМ,
в который входят десятки различных систем.

33.

Разделы
Агентное (имитационно-статистическое) моделирование –
Низкий уровень абстракции
Дискретно-событийное моделирование
(аналог Марковских цепей) – средний уровень
абстракции
Системная динамика (аналог Марковских процессов и
систем дифференциальных уравнений Колмогорова) –
высокий уровень абстракции
Возможно составление моделей с использованием
всех разделов одновременно
33

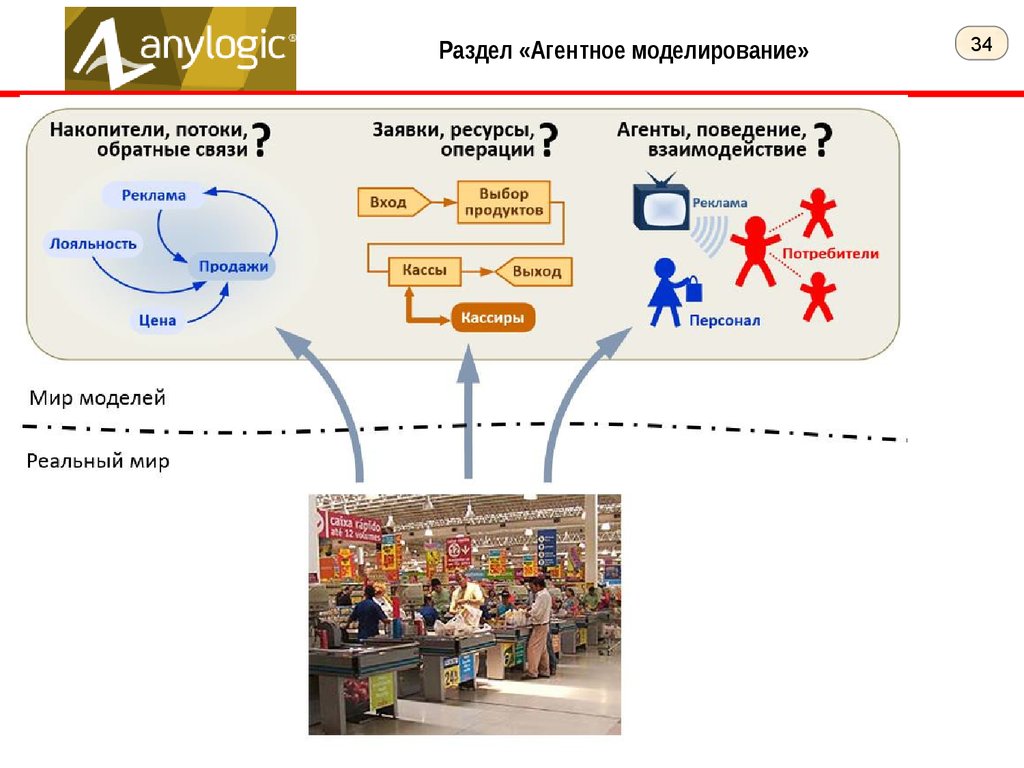
34.

Раздел «Агентное моделирование»
34

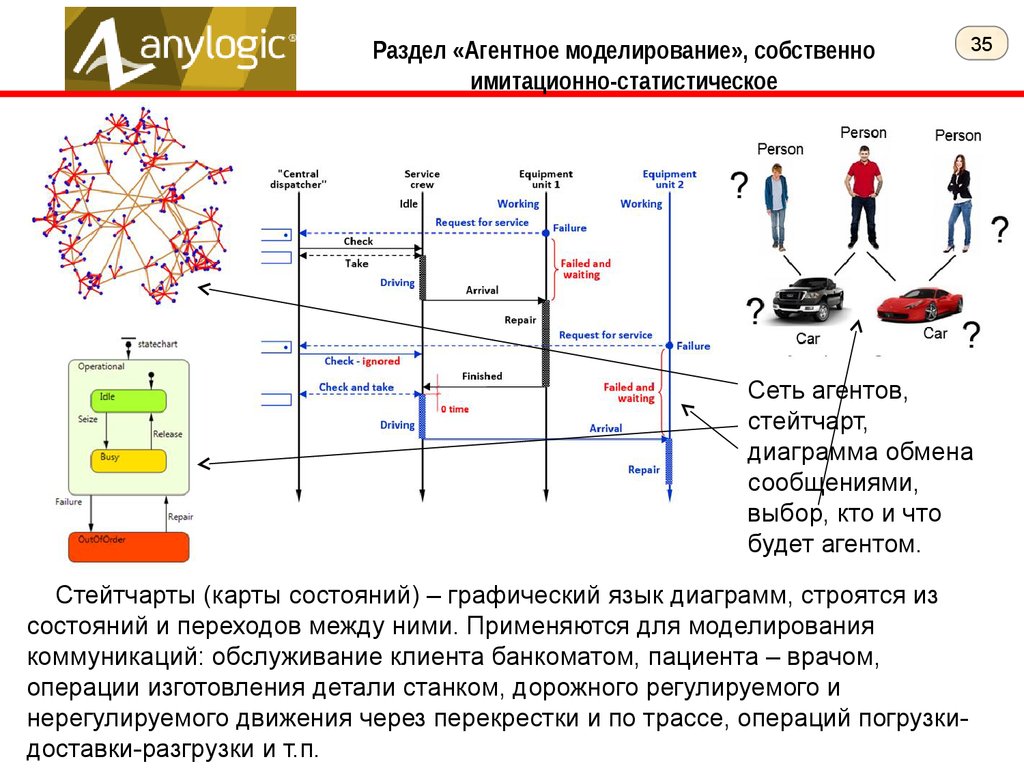
35.

Раздел «Агентное моделирование», собственно
имитационно-статистическое
35
Сеть агентов,
стейтчарт,
диаграмма обмена
сообщениями,
выбор, кто и что
будет агентом.
Стейтчарты (карты состояний) – графический язык диаграмм, строятся из
состояний и переходов между ними. Применяются для моделирования
коммуникаций: обслуживание клиента банкоматом, пациента – врачом,
операции изготовления детали станком, дорожного регулируемого и
нерегулируемого движения через перекрестки и по трассе, операций погрузкидоставки-разгрузки и т.п.

36.

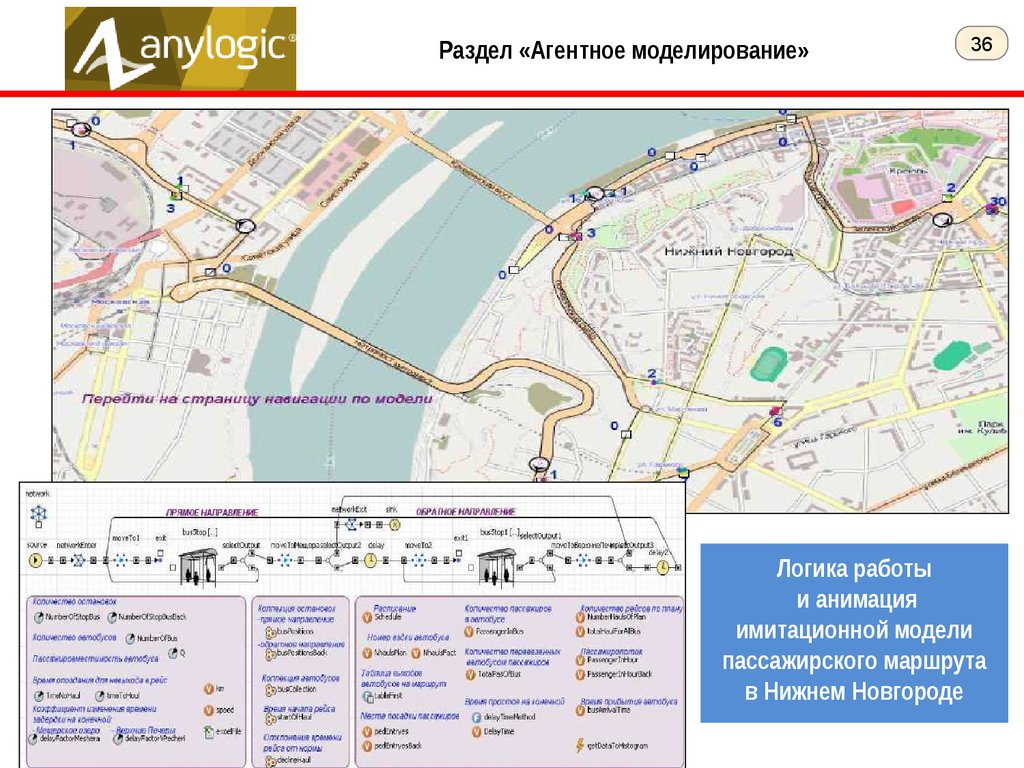
Раздел «Агентное моделирование»
36
Логика работы
и анимация
имитационной модели
пассажирского маршрута
в Нижнем Новгороде

37.

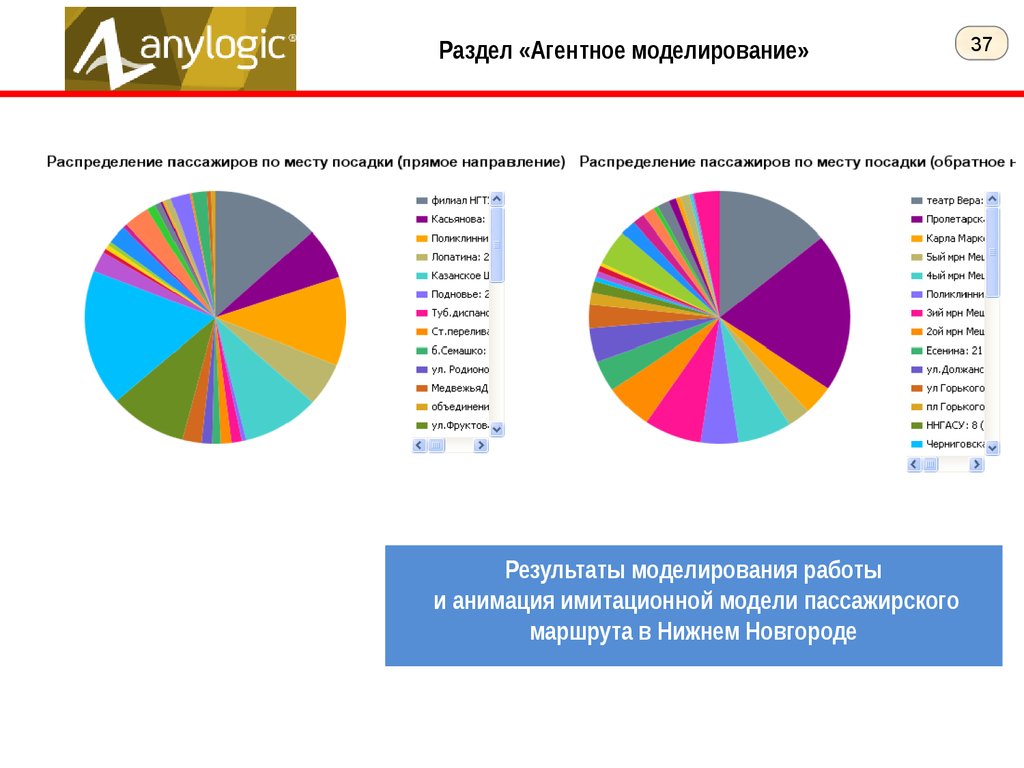
Раздел «Агентное моделирование»
Результаты моделирования работы
и анимация имитационной модели пассажирского
маршрута в Нижнем Новгороде
37

38.

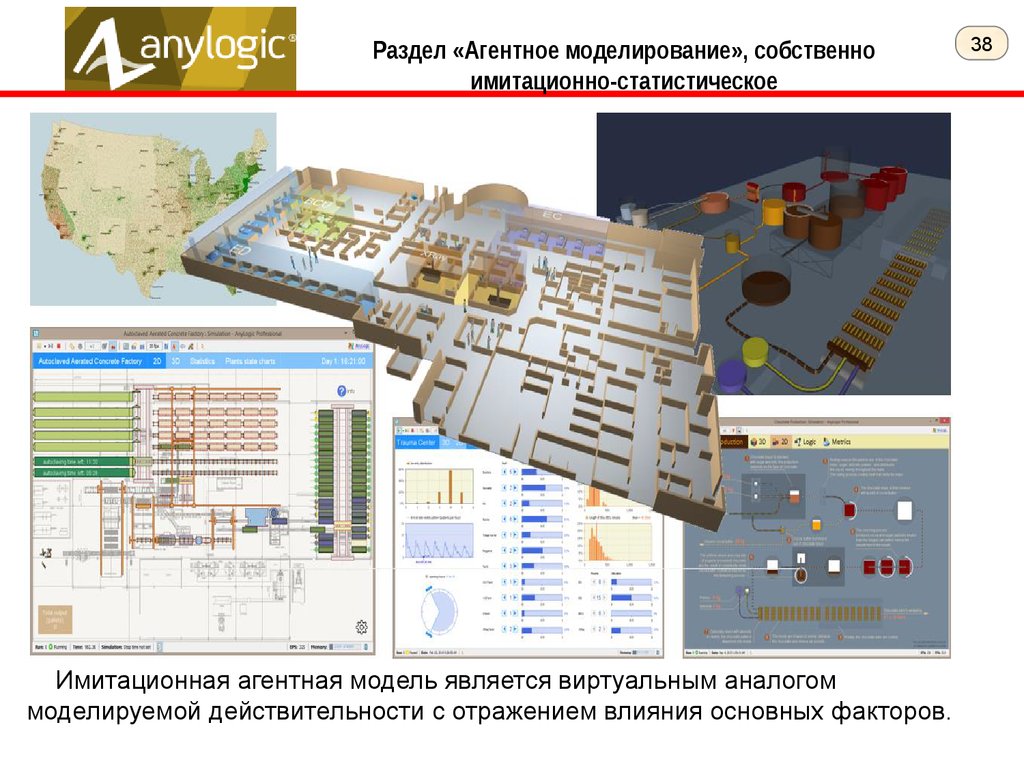
Раздел «Агентное моделирование», собственно
имитационно-статистическое
Имитационная агентная модель является виртуальным аналогом
моделируемой действительности с отражением влияния основных факторов.
38

39.

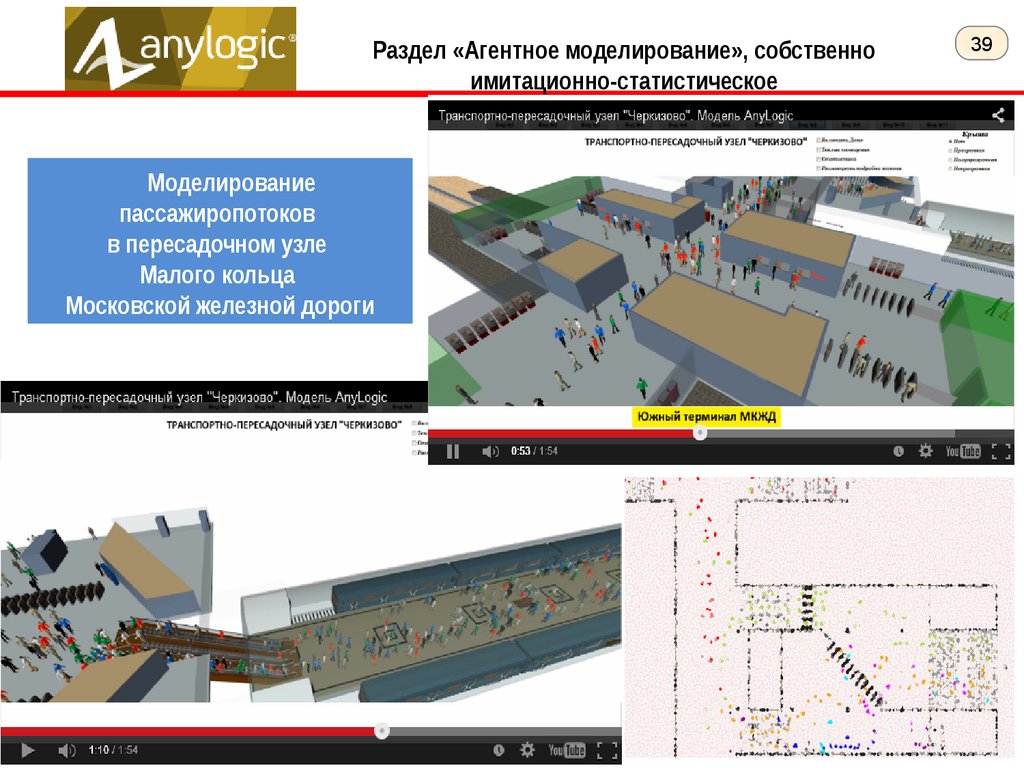
Раздел «Агентное моделирование», собственно
имитационно-статистическое
Моделирование
пассажиропотоков
в пересадочном узле
Малого кольца
Московской железной дороги
39

40.

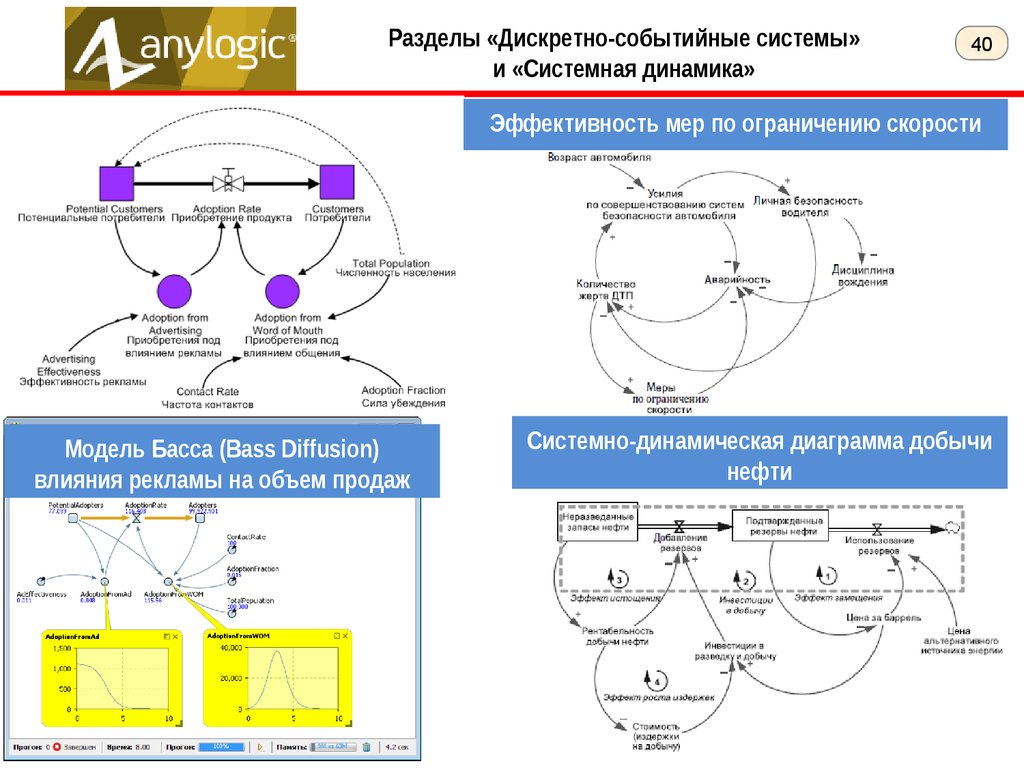
Разделы «Дискретно-событийные системы»
и «Системная динамика»
40
Эффективность мер по ограничению скорости
Модель Басса (Bass Diffusion)
влияния рекламы на объем продаж
Системно-динамическая диаграмма добычи
нефти

41.

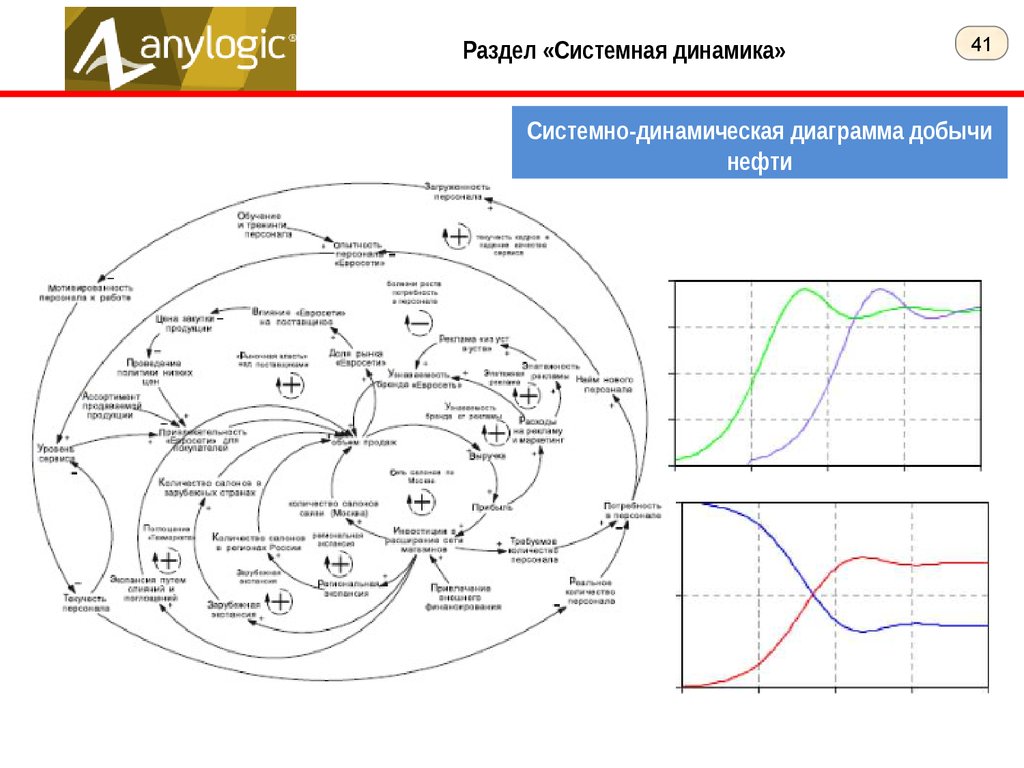
Раздел «Системная динамика»
41
Системно-динамическая диаграмма добычи
нефти

42.

Общий логико-вероятностный метод
42
• Задачи, которыми занимается наука и которые
она умеет решать − в основном задачи на
детерминированных системах с двумя или тремя
переменными.
• Подобные задачи, имеющие в своей основе
малое число переменных, решение которых
ищется в аналитической форме, называют
задачами организованной простоты.
• Методы решения − информационные технологии
организованной простоты.
• Задачи анализа больших (сложных), или трудно
формализуемых, или плохо организованных систем
представляют собой задачи неорганизованной
сложности.
• Методы решения этих задач, имеющие в своей основе большое число
переменных и статистическую основу динамики средних, называют
информационными технологиями неорганизованной сложности.
• Задачи, связанные со средней частью спектра сложностей, имеющие
в своей основе отображение структурных взаимосвязей всех или
основных элементов, называют задачами организованной сложности,
а методы их решения – информационными технологиями
организованной сложности.

43.

Общий логико-вероятностный метод
• Логико-вероятностный метод (ЛВМ)
представляет собой информационную
технологию организованной сложности,
позволяющую отслеживать одновременно и
поэлементно все взаимосвязи и
взаимодействия в структурно сложных
технических системах.
• Общий логико-вероятностный метод (ОЛВМ)
является высшей формой и практической
реализацией ЛВМ в области так называемых
немонотонных систем, систем, отражающих
противоборство, конкурентную и вооруженную
борьбу, т.е. представляет собой
информационную технологию анализа
экономического и вооруженного
противоборства.
43

44.

Общий логико-вероятностный метод
• Отечественные ученые – создатели информационной технологии
ЛВМ, ОЛВМ и автоматизированной методики
их применения
ЛВМ
ОЛВМ и ПК АСМ
Александр Сергеевич Можаев,
доктор технических наук,
профессор,
капитан 1 ранга
44

45.

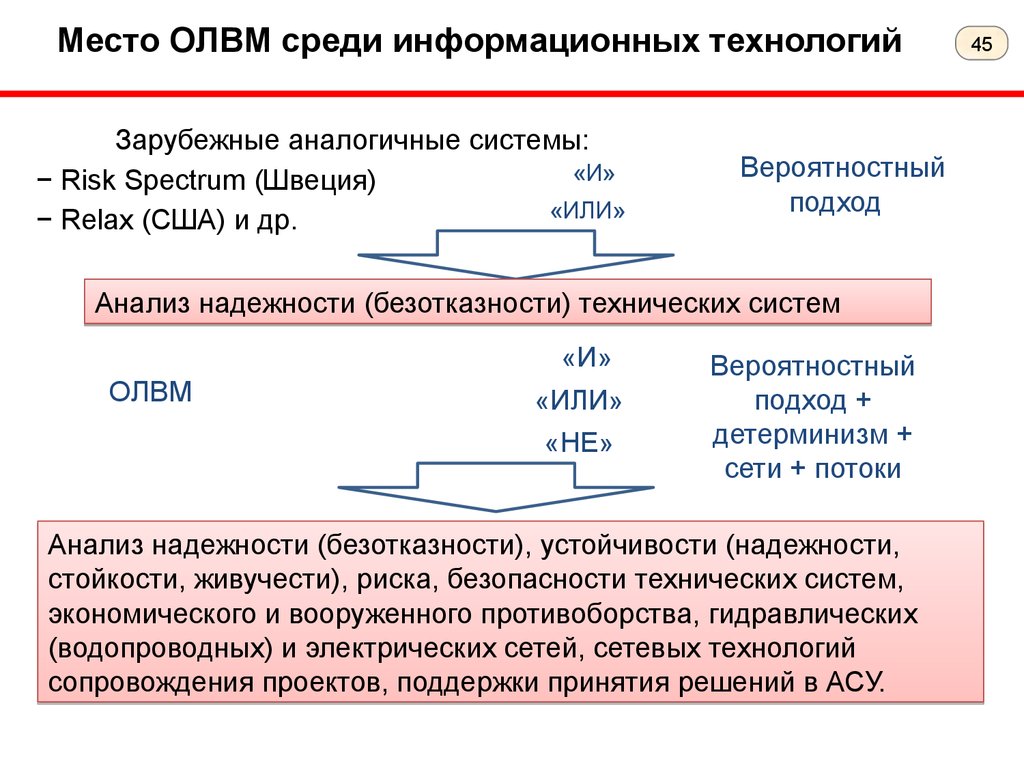
Место ОЛВМ среди информационных технологий
Зарубежные аналогичные системы:
«И»
− Risk Spectrum (Швеция)
«ИЛИ»
− Relax (США) и др.
Вероятностный
подход
Анализ надежности (безотказности) технических систем
«И»
ОЛВМ
«ИЛИ»
«НЕ»
Вероятностный
подход +
детерминизм +
сети + потоки
Анализ надежности (безотказности), устойчивости (надежности,
стойкости, живучести), риска, безопасности технических систем,
экономического и вооруженного противоборства, гидравлических
(водопроводных) и электрических сетей, сетевых технологий
сопровождения проектов, поддержки принятия решений в АСУ.
45

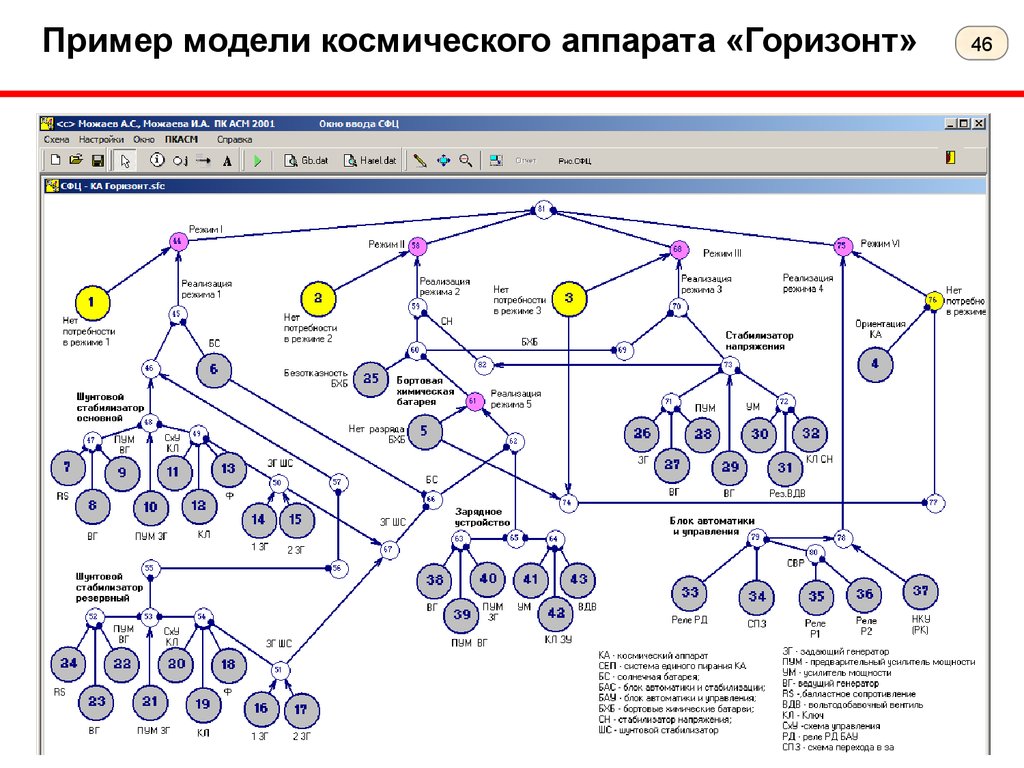
46.

Пример модели космического аппарата «Горизонт»
46

47.

Пример модели вооруженного противоборства
47

48.

Пример модели вооруженного противоборства
48

49.

49
Результат моделирования вооруженного противоборства

50.

Форсайт-технология
50
Форсайт (от англ. Foresight – взгляд в будущее, предвидение) – это
технология оценивания долгосрочных перспектив любой области
деятельности высшей сферы руководства, масштаба региона, отрасли,
страны, чтобы определить стратегические направления принимаемых
решений, способные принести наибольший успех с наименьшим риском.
Место и роль Форсайта определяются следующими его особенностями:
– это обязательно экспертиза (коллективный опрос специалистов,
публикации, научные результаты);
– это ориентация не на попытку угадать самый вероятный вариант развития
событий, а на поиск компромиссных решений для всех возможных вариантов
будущего;
– это высокая степень неопределенности внешних условий и факторов,
свойственная высшей сфере политической, социальной, экономической, военнотехнической деятельности;
это совокупность современных разнообразных технологических (методических)
средств для прогноза стратегического масштаба: метода Дельфи (экспертного
опроса), метода сценариев, дорожных карт, мозгового штурма и др.

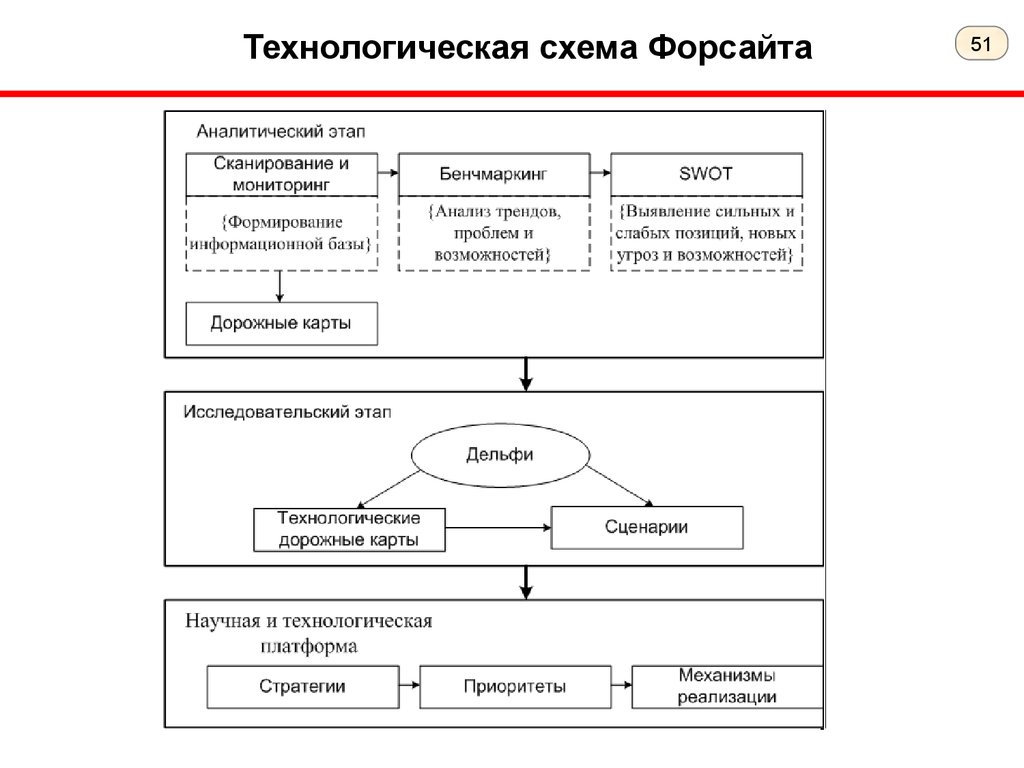
51.

Технологическая схема Форсайта
51

52.

Аналитический этап Форсайта
52
Задачей аналитического этапа является формирование информационной
базы для всей системы и проведение анализа сформировавшихся трендов
(тенденций), сильных и слабых позиций, новых угроз и возможностей по кругу
социальных, экономических, экологических, а также научных и технологических
факторов.
Необходимо размежевывать сканирование и мониторинг.
Сканирование имеет задачей главным образом обзор предметной сферы и
внешних условий, состояния процесса, отрасли.
Мониторинг направлен на выявление тенденций, трендов изменения
внешних условий и состояния процесса, отрасли.
Информационной базой для мониторинга изменений служат результаты
периодического сканирования.

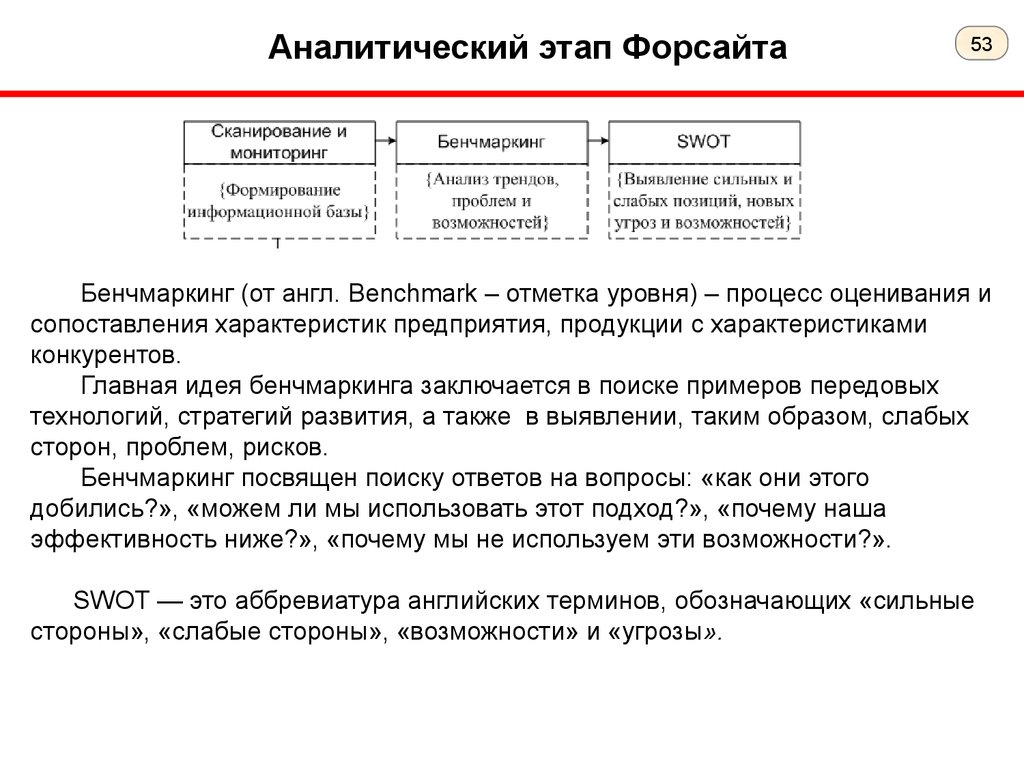
53.

Аналитический этап Форсайта
53
Бенчмаркинг (от англ. Benchmark – отметка уровня) – процесс оценивания и
сопоставления характеристик предприятия, продукции с характеристиками
конкурентов.
Главная идея бенчмаркинга заключается в поиске примеров передовых
технологий, стратегий развития, а также в выявлении, таким образом, слабых
сторон, проблем, рисков.
Бенчмаркинг посвящен поиску ответов на вопросы: «как они этого
добились?», «можем ли мы использовать этот подход?», «почему наша
эффективность ниже?», «почему мы не используем эти возможности?».
SWOT — это аббревиатура английских терминов, обозначающих «сильные
стороны», «слабые стороны», «возможности» и «угрозы».

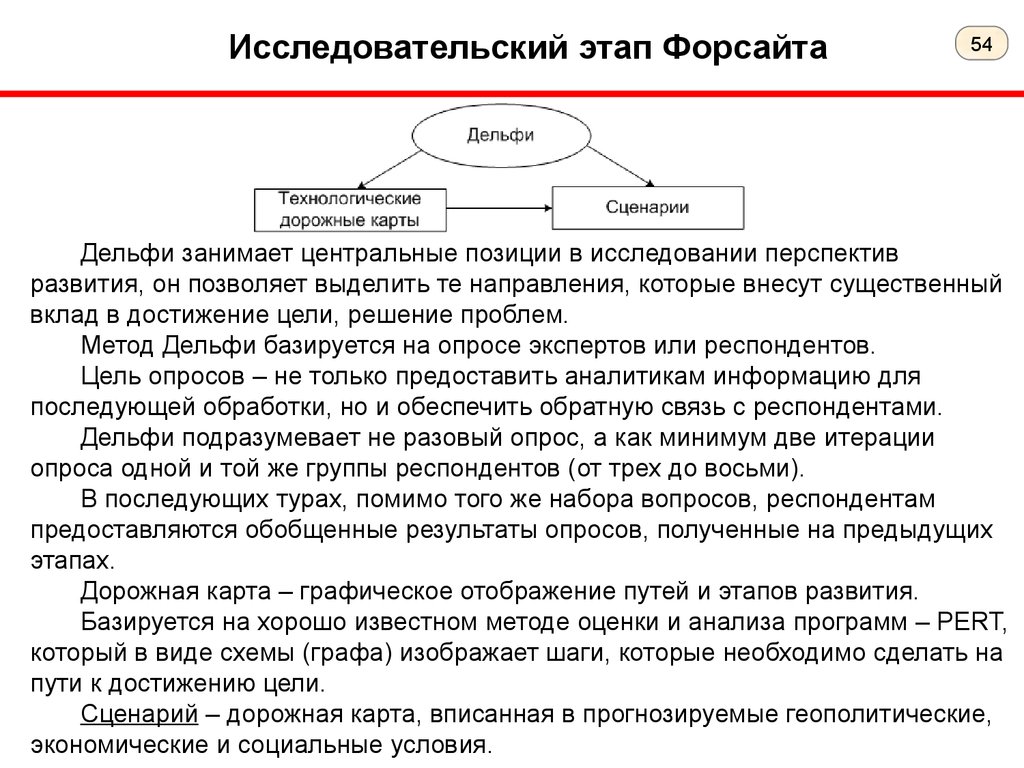
54.

Исследовательский этап Форсайта
54
Дельфи занимает центральные позиции в исследовании перспектив
развития, он позволяет выделить те направления, которые внесут существенный
вклад в достижение цели, решение проблем.
Метод Дельфи базируется на опросе экспертов или респондентов.
Цель опросов – не только предоставить аналитикам информацию для
последующей обработки, но и обеспечить обратную связь с респондентами.
Дельфи подразумевает не разовый опрос, а как минимум две итерации
опроса одной и той же группы респондентов (от трех до восьми).
В последующих турах, помимо того же набора вопросов, респондентам
предоставляются обобщенные результаты опросов, полученные на предыдущих
этапах.
Дорожная карта – графическое отображение путей и этапов развития.
Базируется на хорошо известном методе оценки и анализа программ – PERT,
который в виде схемы (графа) изображает шаги, которые необходимо сделать на
пути к достижению цели.
Сценарий – дорожная карта, вписанная в прогнозируемые геополитические,
экономические и социальные условия.

55.

Научная и технологическая платформа Форсайта
55
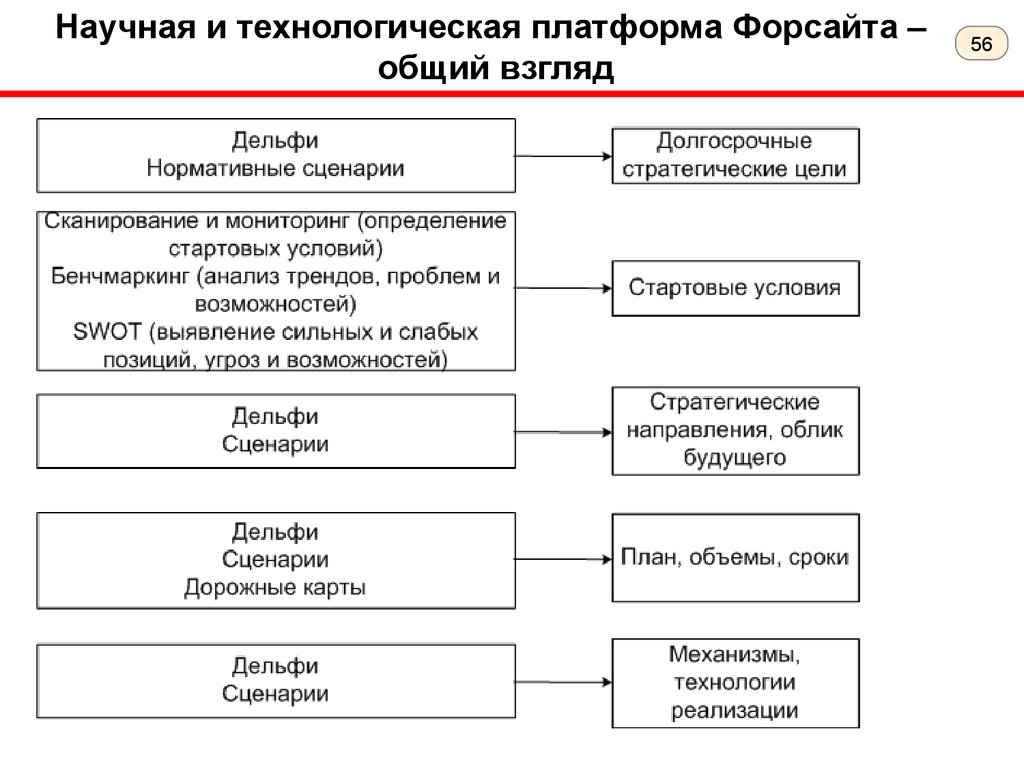
Научная и технологическая платформа должна включать следующие блоки.
– долгосрочные стратегические цели;
– краткую характеристику стартовых условий, включая сильные и слабые
стороны, открывающиеся новые возможности и угрозы:
– стратегические направления для достижения поставленных целей;
– приоритетные направления развития ;
– план действий и комплекс механизмов и мер для поддержки
приоритетных технологий.

56.

Научная и технологическая платформа Форсайта –
общий взгляд
56

57.

Литература
57
1. Бейтсон. Г. Экология разума, СМЫСЛ, М., 2000.
2. Берж. К. Теория графов и ее применение, ИЛ, М., 1962.
3. Дубовский С.В. Объект моделирования - цикл Кондратьева, Математическое
моделирование, т.7, N6./ 1995.
4. Калужанин Л.А., В.И.Сущанский. Преобразования и перестановки, М., Наука,
Главная редакция физико-математической литературы, 1985.
5. Оре О. Графы и их применения, “Мир”, М., 1965.
6. Плотинский Ю.М. Модели социальных процессов.- М.: Логос, 2001.
7.
Робертс Ф. С. Дискретные математические модели с приложениями к социальным
биологическим и экологическим задачам, Наука-Физматлит, 1986.
8.
Самарский А.А., Михайлов А.П. Математическое моделирование (Идеи, методы и
примеры), Наука-Физматлит, 1997.
9. Толстова Ю.Н. Концептуальное моделирование предметной области исследования при
изучении социальной напряженности//Традиции и современность в социологии. –
М.: МАКС Пресс, 2001 – 324 с.
10. Шведовский В.А. Детерминизм и статистичность в динамических моделях, СоцИс,
1985, 1.
11.
Шведовский
В.А.,
Шведовская
Т.Л.
Информационно-потоковый
подход
к
формированию информационно-культурного кода, Российский монитор, 8, 1997.
12. Шведовский В.А. Социальные коды России и проблема выбора направления ее стратегического
развития, II Всероссийская научная конференция "Россия- XXI век" (тезисы докладов), Совет
Федерации Федерального Собрания РФ, Министерство науки и технологий РФ, Российская
Академия Наук, Министерство образования РФ, М., 1999.
13. Ядов В.А. Социологическое исследование: методология, программы, методы, М., Наука, 1987.
14. Яковец Ю.В. Циклы Кризисы Прогнозы, Наука, М., 1999.

58.

Литература
58
15. Шведовский В.А. О языке сопровождения вычислительного эксперимента для математических
моделей социальных процессов // Математическое моделирование социальных процессов. – М.,
1989
16. Плотинский Ю.М. Теоретические и эмпирические модели социальных процессов, Логос, М., 1998 г.
17. Лебедев В.В. Математическое моделирование социальных процессов, 1998
18. Математические методы в современной буржуазной социологии (под ред. Э.П.Андреева и
Г.В.Осипова), 1966.
19. Моделирование социальных процессов (под ред. Э.П. Андреева и Ю.Н. Гаврильца) 1970.
20. Найдыш В.М. Концепции современного естествознания, Гардарики, М., 1999, стр 395-418.
21. Чайковский Ю.В. О познавательных моделях // Исследования по математической биологии. –
Пущино, 1996
22. Шикин Е.В., Шикина Г.Е. Математика: Пути знакомства; Основные понятия; Методы; Модели:
Учебник для вузов. Изд. 2-е, испр., доп. Серия: Гуманитариям о математике, 2001,- 272с.
Гуманитариям о математике/ Центр естественно-научного образования гуманитариев – М.: Агар,
1999 – 332 с.
23. Гребнев Л.С. Философия экономики, Луч, 1991.
24. Кочетов Э.Г. Геоэкономика, 1999.
25. Яблоков А.В., Юсуфов А.Г. Эволюционное учение, “Высшая школа’, М., 1998, стр. 235.
26. Мешкова и др. Введение в психогенетику человека, М., 1999.
27. А.Кофман, Р.Фор. Займемся исследованием операций, «МИР», М., 1966.
28. Гоппа В.Д. Введение в алгебраическую теорию информации, Физмат., М., 1995.
29. Бехтерев В.М. Когнитивная рефлексология, Колос, Петроград, 1921.
30. Каракозова Э.В. Моделирование в общественных науках, ВШ, М., 1986.