Similar presentations:
Упругий режим
1. Упругий режим
2.
При этом режиме вытеснение нефти происходит поддействием упругого расширения самой нефти,
окружающей нефтяную залежь воды и скелета
пласта. Условием существования этого режима
является
Р пл Р нас
3.
Геологическими условиями, благоприятствующимисуществованию упругого режима, являются:
< залежь закрытая, не имеющая регулярного питания;
< обширная водонасыщенная зона, находящаяся за
пределами контура нефтеносности; отсутствие газовой
шапки;
< наличие эффективной гидродинамической связи
нефтенасыщенной части пласта с законтурной областью;
< превышение пластового давления над давлением
насыщения.
4.
При разработке залежи в условиях упругогорежима быстрое понижение давления
происходит в пределах самой залежи,
во всей системе, питающей залежь упругой
энергией давления (в законтурной области),
снижается медленно.
5. ХАРАКТЕРИСТИКИ
1. Коэффициент упругоемкости пласта* m ж с
2. Коэффициент пьзопроводности
K
*
3. Коэффициент гидропроводности
kh
.
6. Подсчет упругого запаса жидкости в пласте
• Под упругим запасов жидкости в пластепонимается количество жидкости, которое
можно извлечь из пласта при снижении
давления в нем за счет объемной упругости
пласта и насыщающих его жидкостей.
V з V ж Vп
V ж жV ж Р
Vп сVп Р
7.
• Коэффициент объемной упругости жидкости жхарактеризует податливость жидкости изменению
ее объема и показывает, на какую часть
первоначального объема изменяется объем
жидкости при изменении давления на единицу:
ж
1 dVж
V ж dP
Для различных нефтей отечественных
месторождений н=(7 30) 10-1 1/ГПа; для
пластовых вод в=(2,7 5) 10-1 1/ГПа;
для пород, слагающих продуктивные пласты,
с=(0,3 2) 10-1 1/ГПа.
8.
Сжимаемость пластовой нефти обусловливаетсятем, что, как и все жидкости, нефть обладает
упругостью, которая измеряется коэффициентом
сжимаемости (или объемной упругости) βн:
βн
1 ΔV
V ΔP
Коэффициент сжимаемости зависит от давления,
температуры, состава нефти и газового фактора.
9.
V з m ж с Vп РКоэффициент
упругоемкости * численно
равен изменению упругого
запаса жидкости в единице
объема
пласта
при
изменении в нем давления
на единицу.
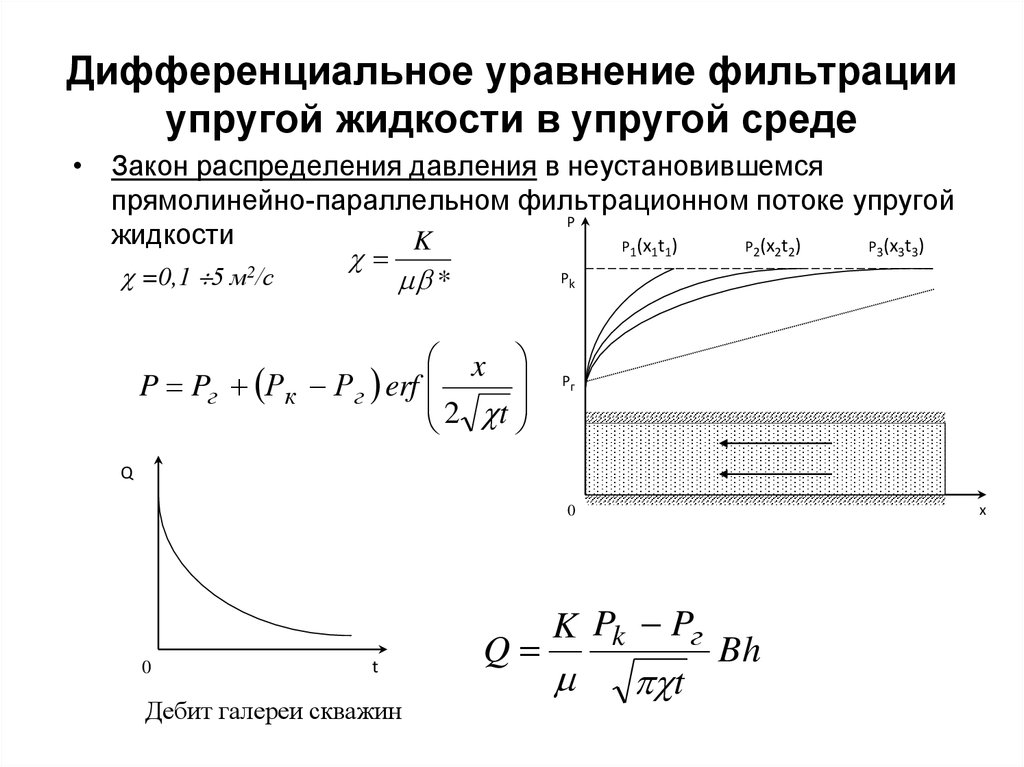
10. Дифференциальное уравнение фильтрации упругой жидкости в упругой среде
• Закон распределения давления в неустановившемсяпрямолинейно-параллельном фильтрационном потоке упругой
P
жидкости
K
P1(x1t1)
P2(x2t2)
P3(x3t3)
Pk
=0,1 5 м2/с
*
x
P Pг Рк Рг erf
2 t
Pг
Q
x
0
0
t
Дебит галереи скважин
Q
K Pk Pг
t
Bh
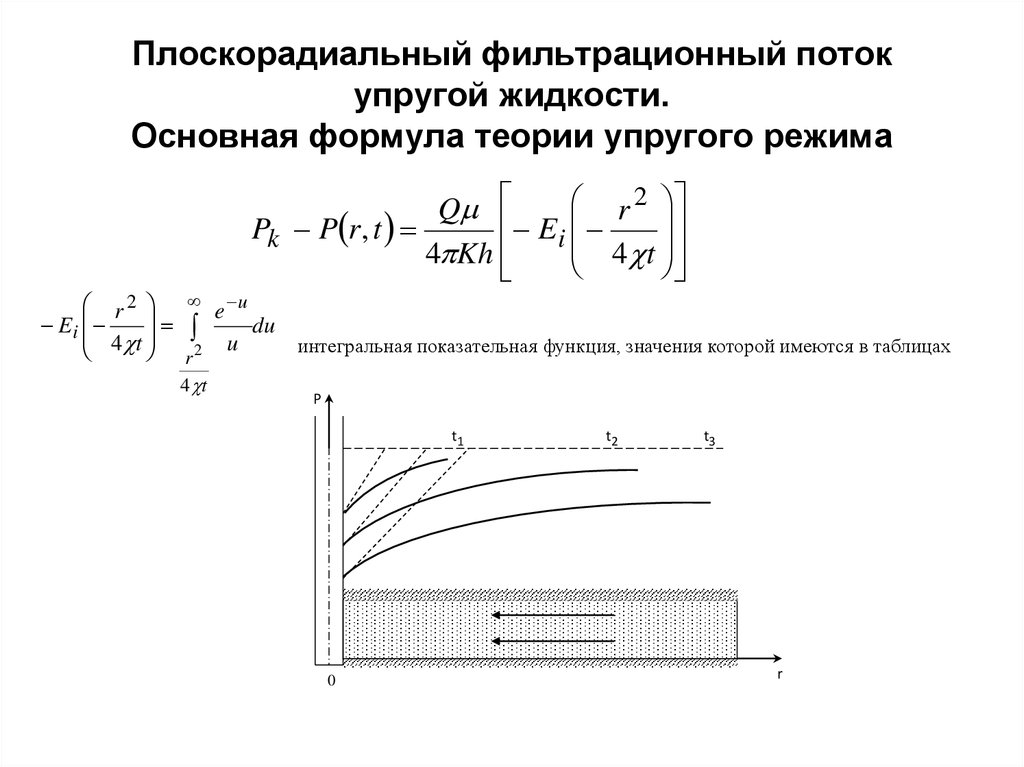
11. Плоскорадиальный фильтрационный поток упругой жидкости. Основная формула теории упругого режима
r 2Q
Pk P r , t
E i
4 t
4 Kh
r 2 e u
Ei
u du интегральная показательная функция, значения которой имеются в таблицах
4 t
r2
4 t
P
t1
0
t2
t3
r
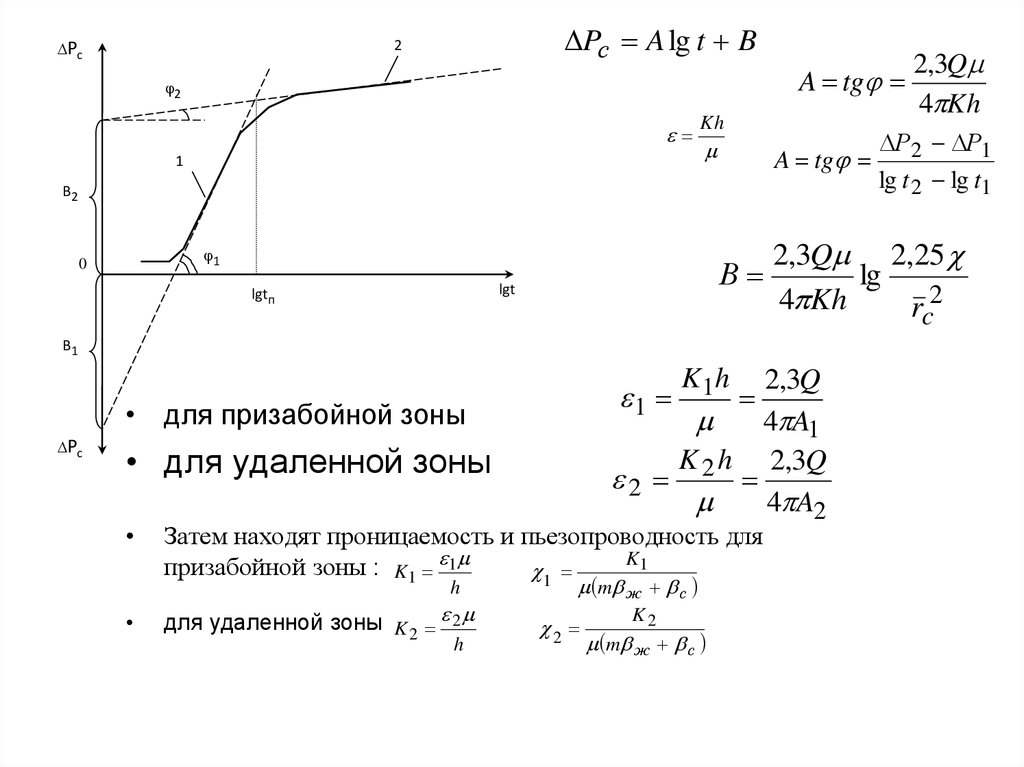
12. Определение коллекторских свойств пласта по данным исследования скважин на неустановившемся режиме
• Гидродинамические методы исследования пластов и скважин,связанные с замерами пластовых и забойных давлений,
называются пьезометрическими.
• при гидродинамическом исследовании измеряют
восстановление забойного давления после остановки скважины,
ранее продолжительное время работавшей с постоянным
дебитом. Давление измеряют с помощью скважинных
глубинных манометров и строят график изменения давления с
течением времени – кривую восстановления давления (КВД).
13.
Pс A lg t B2
Рс
2
1
A tg
Kh
A tg
В2
lgt
lgtп
В1
K h 2,3Q
1 1
4 A1
• для призабойной зоны
Рс
• для удаленной зоны
2
K 2h
Затем находят проницаемость и пьезопроводность для
K1
призабойной зоны : K1 1
1
h
m ж с
для удаленной зоны K 2 2
h
Р2 Р1
lg t 2 lg t1
2,3Q 2,25
В
lg
4 Kh
rc2
1
0
2,3Q
4 Kh
2
K2
m ж с
2,3Q
4 A2
14. ОДНОМЕРНЫЕ УСТАНОВИВШИЕСЯ ФИЛЬТРАЦИОННЫЕ ПОТОКИ ГАЗА
K P PP
dP C
P
P P dP C
функция Л.С.Лейбензона
Жидкость
K dP
Q
f S ,
dS
где Q=const – объемный расход жидкости;
f(S) – площадь поперечного сечения струи
Газ
Qm Q
K
P
dP
f S
dS
K dP
f S ,
dS
где Qь= Q=const – массовый расход газа
Несжимаемая жидкость
Газ
объемный расход Q
-
массовый расход Qm
давление Р
-
функция Л.С.Лейбензона P
объемная скорость фильтрации V
-
массовая скорость фильтрации V
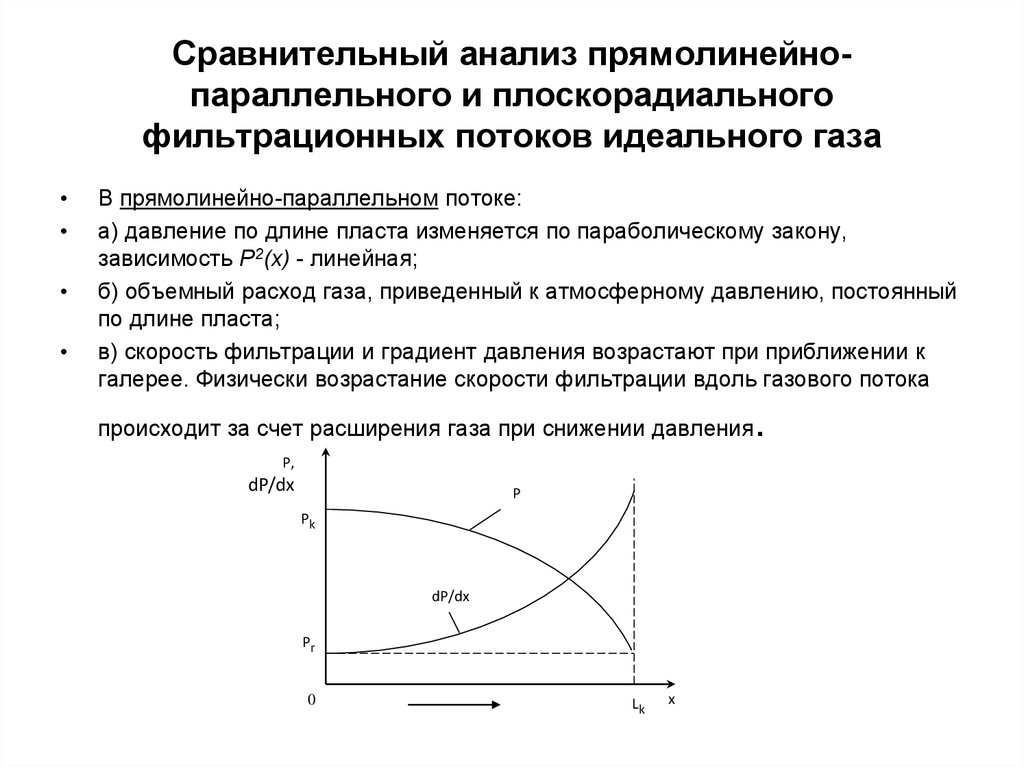
15. Сравнительный анализ прямолинейно-параллельного и плоскорадиального фильтрационных потоков идеального газа
Сравнительный анализ прямолинейнопараллельного и плоскорадиальногофильтрационных потоков идеального газа
В прямолинейно-параллельном потоке:
а) давление по длине пласта изменяется по параболическому закону,
зависимость Р2(x) - линейная;
б) объемный расход газа, приведенный к атмосферному давлению, постоянный
по длине пласта;
в) скорость фильтрации и градиент давления возрастают при приближении к
галерее. Физически возрастание скорости фильтрации вдоль газового потока
происходит за счет расширения газа при снижении давления
Р,
dP/dx
Р
Pk
dP/dx
Pг
0
Lk
x
.
16.
Индикаторная диаграмма при фильтрации газа строится в координатахВ плоскорадиальном потоке:
а) распределение давления подчинено логарифмическому и
полулогарифмическому законам, поэтому в газовом потоке, в отличие от потока
жидкости, имеет место резкое падение давления вблизи скважины и весьма
малое – вдали от нее. Площадь и объем пласта с пониженным давлением
вблизи скважины значительно меньше объема газового пласта в целом.
Поэтому в газонасыщенном пласте давление повсюду считается одинаковым,
приблизительно равным давлению на контуре питания;
б) градиент давления и скорость фильтрации вблизи забоя газовой скважины
резко возрастают как за счет уменьшения r, так и за счет падения давления Р
0
Рк2-Рс2
Qат
.
Индикаторная диаграмма при фильтрации газа
2
2
строится в координатах Qат Pk Pc и в
установившемся плоскорадиальном потоке имеет
прямолинейный характер
17. Многофазные фильтрации
18. Двухфазная фильтрация
При совместном движении двух (или более)флюидов, каждый из них занимает только
часть порового пространства.
Насыщенность элемента пористой среды
данной фазой Si = Vi/ Vn, где i= 1,2 (S1, S2—
насыщенность смачивающей и
несмачивающей фазами), Vi — объем
среды, занятой жидкостью, Vn— общий
объем активных пор в данном элементе.
S1 + S2=1,S1=S.
19. Закон Дарси
1k p1
1
1L
Закон Дарси
k 2 p 2
2
2L
где 1 и 2 — скорости фильтрации фаз; 12—
динамические коэффициенты вязкости жидкостей;
p12— разности давлений в соответствующих фазах;
k12* — фазовые проницаемости, зависящие от
природы пористой среды, ее абсолютной
проницаемости k, от насыщенности пористой среды
каждой фазой.
При описании двухфазных течений обычно вместо
фазовых проницаемостей вводят
«относительныепроницаемости» kiфаз,
определяемые из отношений:
k12 =
12
k
k
20.
Закон Дарси для каждой из фаз :k i (S ) pi
i k
i L
Здесь и далее индекс i = 1 будем относить к более смачивающей
фазе - воде (в системе вода-нефть), а индекс i = 2 - к менее
смачивающей жидкости - нефти;
21.
Для каждой фазы существует предельнаянасыщенность такая, что при меньших значениях
насыщенности эта фаза неподвижна.
Движение первой фазы может происходить только в
том случае, если S>S* (для водонефтяной системы
S* называют насыщенностью связанной водой).
Для второй фазы связанная насыщенность 1—S*и
называется остаточной нефтенасыщенностью.
Сумма относительных проницаемостей для каждого
фиксированного значения S меньше 1:
k1(S) + k2(S) 1
0<S<1.
22.
23.
Относительная проницаемость смачивающей фазыпри S*имеет значение меньше 1, тогда как величина
к2(S) при S*, близка к единице.
Это означает, что присутствие связанной
смачивающей фазы мало влияет на течение
несмачивающей жидкости, тогда как присутствие
остаточной несмачивающей фазы значительно
«стесняет» движение смачивающей фазы.
Пласт считается созревшим для разработки, если
остаточная водонасыщенность
S 25%
B
24. Обобщенный закон Дарси для трехфазной фильтрации
25.
• При содержании в породе более 35% газадвижущейся фазой является только газ, а вода и
нефть, занимающие оставшийся объем пор,
неподвижны.
• При содержании газа меньше 10% и нефти меньше
23% поток содержит одну воду, а при насыщенности
водой от 20 до 30% и газом от 10 до 18% в движении
участвует только нефть.
• Затененные области, примыкающие к той или иной
стороне треугольной диаграммы, отвечают
одновременному движению двух фаз: газ-вода, воданефть и газ-нефть. В центре диаграммы
расположена область насыщенностей, при которых в
потоке одновременно движутся три фазы.
26.
• Вершины треугольной диаграммы соответствуют100%-ному насыщению пористой среды одной из
фаз.
• Противоположные эти вершинам стороны
соответствуют отсутствию данной фазы в породе.
• В каждой точке внутри треугольной диаграммы
сумма насыщенностей равна единице.
• Кривые линии отделяют на диаграмме возможные
области одно-, двух- или трехфазного течения.
27.
• Насыщенности фаз Siудовлетворяют равенству:
• S1+S2+S3=1.
• При этом следует иметь ввиду, что
фазовые проницаемости являются
уже функциями двух независимых
насыщенностей Sн и Sв
(газонасыщенность Sг=1-Sн-Sв):
Кн=Кн(Sн,Sв);
Кв=Кв(Sн,Sв);
Кг=Кг(Sн,Sв).
28.
• С. А. Христиановичем была показанавозможность сведения нелинейных
задач установившейся фильтрации
газожидкостных систем к задачам
движения однородной несжимаемой
жидкости в пористой среде:
• Н(р) =
k H ( H B )
k H (p) H (p)dp const
























 industry
industry








