Вероятность события для эксперимента с конечным числом исходов. (Лекция 3-4)

1. §3. Вероятность события для эксперимента с конечным числом исходов

1 , 2 ,..., n
i
P( i ) 0,
P( A)
n
P( ) 1;
i 1
P( );
i A
i
i

2.

Замечание 1.
Замечание 2.
1 , 2 ,..., n ,...
Условие неотрицательности:
i=1,2,…,n,…
Условие нормированности:
P( i ) 0,
P( ) 1;
i 1
i

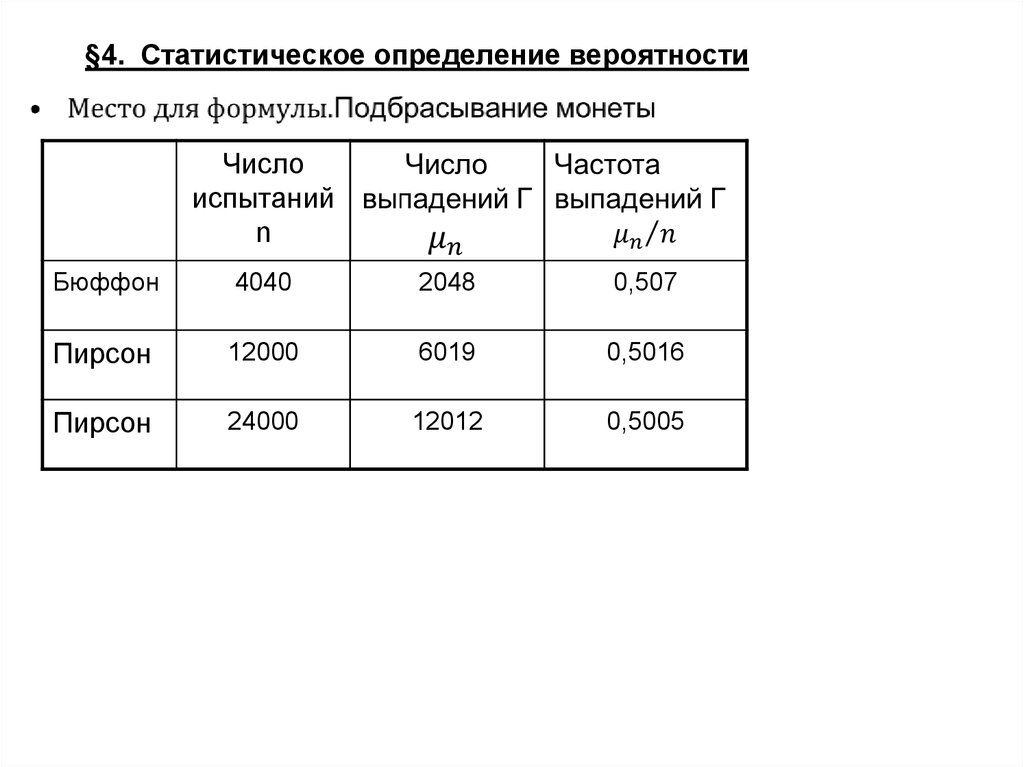
3. §4. Статистическое определение вероятности

Число
испытаний
n
Бюффон
4040
2048
0,507
Пирсон
12000
6019
0,5016
Пирсон
24000
12012
0,5005

4. §5. Геометрическая вероятность

5. .

Задача 29. На прямолинейном участке газопровода длиной 130 км
произошел разрыв. Какова вероятность того, что разрыв удален от
обоих концов участка на расстоянии, большее 50 км?
Решение. Участок газопровода AB разобьем точками разрыва C и D
(рис. 7.7). В нашем случае разрыв должен произойти на участке CD.
Рис. 7.7
Тогда вероятность искомого события равна
.
Ответ: 3/13

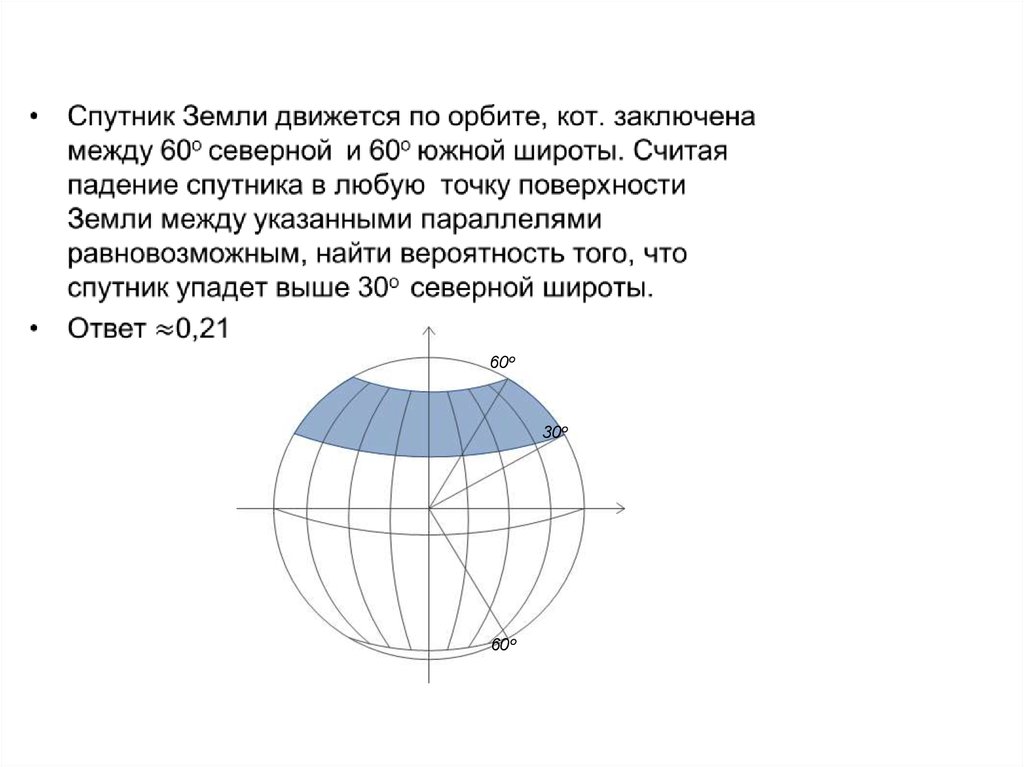
6. Задача

60о
30о
60о

7. III. Условные вероятности. Независимые события.

§1.Вычисление условной вероятности
События А и В, Р(В)>0;
Вероятность события А при условии, что произошло соб-е В, наз-т
условной вероятностью и обозначают Р ( А | B )
a)
Классическая схема
Рассмотрим эксперимент с n равновозможными исходами.
События А и В, Р(В)>0;
A ~ m исходов
B ~ k исходов
AB ~ l
l
Р( А | B) ;
k

8.

b) Общий случай
Опр. Условной вероятностью события А при условии, что
произошло соб. В наз. число Р ( А | B ) , кот. определяется
формулой
Пример
Р( АВ)
Р( А | B)
,
Р( В)
Р( В) 0.
§ 2 Свойства условной вероятности
Формула умножения вероятностей (для любых событий А и В).
Р( АВ) Р( В) Р( А | В) P( A) P( B | A).
Пример

9.

§ 3 Независимые события
3.1 Определение независимых событий
Опр.1 Событие А наз. независимым от события В ( Р(В)>0),
если вероятность наступления соб. А не зависит от того,
произошло соб. В или нет, т.е. Р(А|B)=P(A).
Лемма (о взаимной независимости событий)
Если событие А не зависит от В при Р(В)>0, то и событие В не
зависит от А при Р(А)>0.
Опр.2 События А и В наз. независимыми, если
Р(АB)=P(A)Р(В).

10.

Условие независимости
1. Р(А|В)=Р(А), Р(В)>0;
Р(B|A)=Р(B), Р(A)>0;
2. Р(АВ)=Р(А) P(B)
Пример
Из колоды карт (36) извлекается 1 карта.
А ={ выпал валет };
В ={ выпала карта пиковой масти };
Зависимы или нет А и В ?
Проверим Р(АВ)=Р(А) P(B)

11. .

Пример
Эксперимент состоит в подбрасывании двух монет. Являются ли
независимыми события:
A={ герб выпал на первой монете } и B= { хотя бы раз выпала решка }

12. .

Для независимых
событий
Р(АВ)=Р(А)Р(В)
Для несовместных
событий
Р(АВ)=0, т.к. АВ=Ø

13. Пример

Вероятность попадания в мишень для 1-го стрелка
равна 0.5, для 2-го – 0,4. Каждый стрелок делает по 1
выстрелу.
Какова вероятность того, что в мишени
a)ни одной пробоины;
b)одна пробоина;
c)хотя бы 1 пробоина.

14.  

15. 3.2. События, независимые в совокупности

• Опр. События A1 , A2 ,..., An наз. независимыми в
совокупности, если для любого выбранного из них набора
событий Ai , Ai ,..., Ai вероятность произведения этих
1
2
k
событий равна произведению вер-й, т.е.
P( Ai1 Ai2 Aik ) P( Ai1 ) P( Ai2 ) ... P( Ai );
Пример
Независимость трех событий А,В,С
Р(АB)=P(A)Р(В),
Р(АС)=P(A)Р(С),
Р(ВС)=P(В)Р(С),
Р(АВС)=P(A)Р(В)Р(С)
k

16. Пример