Шифрование

1.

Шифрование
БГА, РТФ
Кафедра ИБ
Зензин Александр
Степанович, к.т.н.
Copyright © 2018

2.

Обзор
1. Симметричные алгоритмы шифрования
2. Алгоритм DES
3. Несимметричные алгоритмы шифрования
4. Алгоритм RSA
5. Односторонние функции шифрования

3.

Симметричные алгоритмы шифрования
Шифрование — это средство обеспечения конфиденциальности данных,
хранящихся в памяти компьютера или передаваемых по проводной или беспроводной сети.
Шифрование является краеугольным камнем всех служб информационной
безопасности, будь то система аутентификации или авторизации, защищенный канал или
средства безопасного хранения данных.
Любая процедура шифрования, превращающая информацию из обычного
«понятного» вида в «нечитабельный» зашифрованный, естественно должна быть дополнена
процедурой дешифрирования, которая, будучи примененной к зашифрованному тексту,
снова приводит его в понятный вид.
Пара процедур - шифрование и дешифрирование - называется криптосистемой.
Обычно криптосистема предусматривает наличие специального параметра — секретного
ключа. Криптосистема считается раскрытой, если найдена процедура, позволяющая
подобрать ключ за реальное время. Сложность алгоритма раскрытия является одной из
важных характеристик криптосистемы и называется криптостойкостью.
В криптографии принято правило Керкхоффа, заключающееся в том, что стойкость
шифра должна определяться только секретностью ключа. Так, все стандартные алгоритмы
шифрования (например, AES, DES, PGP) широко известны, их детальное описание содержится
в легкодоступных документах, но от этого их эффективность не снижается. Система остается
защищенной, если злоумышленнику известно все об алгоритме шифрования, но он не знает
секретный ключ.

4.

Симметричные алгоритмы шифрования
Существует два класса криптосистем — симметричные и асимметричные. В
симметричных схемах шифрования (классическая криптография) секретный ключ
шифрования совпадает с секретным ключом дешифрирования. В асимметричных схемах
шифрования (криптография с открытым ключом) открытый ключ шифрования не совпадает с
секретным ключом дешифрирования.
На рис. 1 приведена классическая модель симметричной криптосистемы,
теоретические основы которой впервые были изложены в 1949 году в работе Клода
Шеннона.
В данной модели три участника:
отправитель, получатель и
злоумышленник. Задача отправителя
заключается в том, чтобы по открытому
каналу передать некоторое сообщение в
защищенном виде. Для этого он
зашифровывает открытый текст X
ключом k и передает шифрованный
текст Y. Задача получателя заключается
в том, чтобы расшифровать У и
прочитать сообщение X. Предполагается,
что отправитель имеет свой источник
ключа. Сгенерированный ключ заранее
по надежному каналу передается
получателю. Задача злоумышленника
заключается в перехвате и чтении
передаваемых сообщений, а также в
имитации ложных сообщений.
Рис. 1. Модель симметричного шифрования

5.

Алгоритм DES
Наиболее популярным стандартным симметричным алгоритмом шифрования
данных является DES (Data Encryption Standard). Алгоритм разработан фирмой IBM и в 1976
году был рекомендован Национальным бюро стандартов к использованию в открытых
секторах экономики. Суть этого алгоритма заключается в следующем (рис. 2).
Данные шифруются поблочно. Перед шифрованием любая форма представления
данных преобразуется в числовую. Числа получают путем применения любой открытой
процедуры преобразования блока текста в число. Например, ими могли бы быть значения
двоичных чисел, полученных слиянием кодов ASCII последовательных символов
соответствующего блока текста. На вход шифрующей функции поступает блок данных
размером 64 бита, он делится пополам на левую (I) и правую (К) части. На первом этапе на
место левой части результирующего блока помещается правая часть исходного блока.
Правая часть результирующего блока вычисляется как сумма по модулю 2 (операция XOR)
левой и правой частей исходного блока. Затем на основе случайной двоичной
последовательности по определенной схеме в полученном результате выполняются побитные
замены и перестановки.
Используемая двоичная последовательность,
представляющая собой ключ данного
алгоритма, имеет длину 64 бита, из которых
56 действительно случайны, а 8
предназначены для контроля ключа.
Рис. 2. Схема шифрования по алгоритму DES

6.

Алгоритм DES
Вот уже более трех десятков лет алгоритм DES испытывается на стойкость. И хотя
существуют примеры успешных попыток «взлома» данного алгоритма, в целом можно
считать, что он выдержал испытания. Алгоритм DES широко используется в различных
технологиях и продуктах, связанных с безопасностью информационных систем. Для того
чтобы повысить криптостойкость алгоритма DES, иногда применяют его усиленный вариант,
называемый «тройным алгоритмом DES», который включает троекратное шифрование с
использованием двух разных ключей. При этом можно считать, что длина ключа
увеличивается с 56 до 112 бита, значит, криптостойкость алгоритма существенно
повышается. Но за это приходится платить производительностью — тройной алгоритм DES
требует в три раза больше времени на реализацию, чем «обычный».
В 2001 году Национальное бюро стандартов США приняло новый стандарт
симметричного шифрования, который получил название AES (Advanced Encryption Standard).
Стандарт AES был разработан в результате проведения конкурса на разработку
симметричного алгоритма шифрования, обладающего лучшим, чем у DES, сочетанием
показателей безопасности и скорости работы. Победителем был признан алгоритм Rijndael,
который и был положен в основу AES. В результате AES обеспечивает лучшую защиту, так
как использует 128-битные ключи (а также может работать со 192- и 256-битными ключами)
и имеет более высокую скорость работы, кодируя за один цикл 128-битный блок в отличие от
64-битного блока DES. В настоящее время AES является наиболее распространенным
симметричным алгоритмом шифрования.

7.

Алгоритм DES
В симметричных алгоритмах главную проблему представляют ключи. Во-первых,
криптостойкость многих симметричных алгоритмов зависит от качества ключа, это
предъявляет повышенные требования к службе генерации ключей. Во-вторых,
принципиальной является надежность канала передачи ключа второму участнику секретных
переговоров. Проблема с ключами возникает даже в системе с двумя абонентами, а в
системе с п абонентами, желающими обмениваться секретными данными по принципу
«каждый с каждым», потребуется п х (п - 1)/2 ключей, которые должны быть сгенерированы
и распределены надежным образом. То есть количество ключей пропорционально квадрату
количества абонентов, что при большом числе абонентов делает задачу чрезвычайно
сложной. Несимметричные алгоритмы, основанные на использовании открытых ключей,
снимают эту проблему.

8.

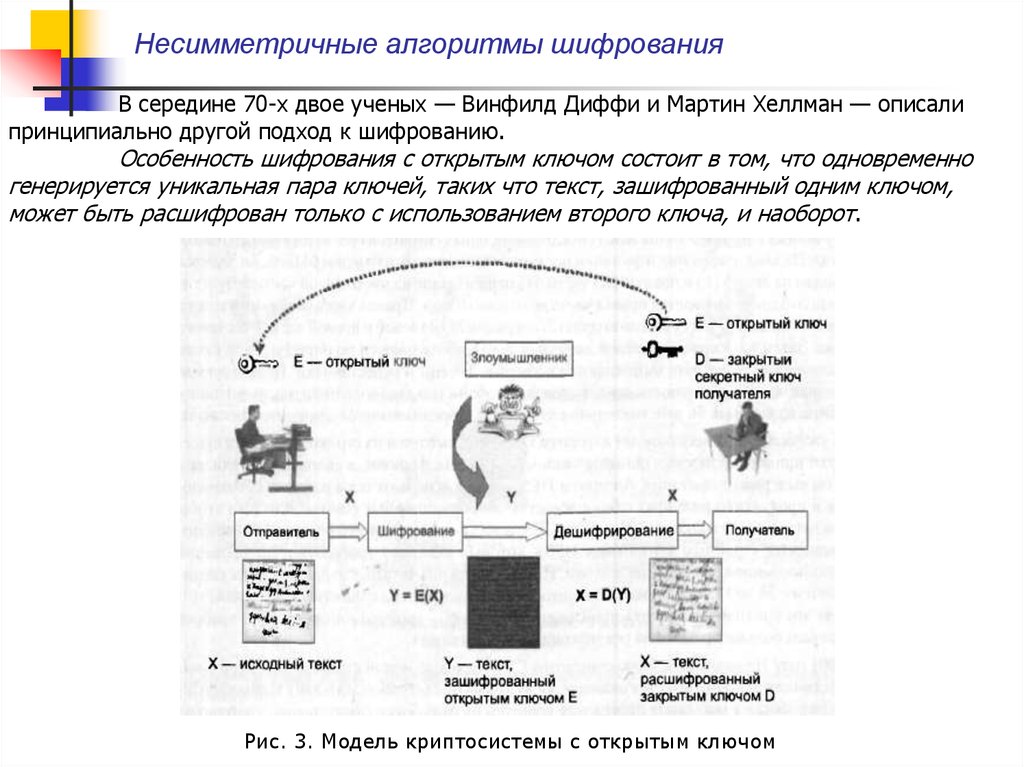
Несимметричные алгоритмы шифрования
В середине 70-х двое ученых — Винфилд Диффи и Мартин Хеллман — описали
принципиально другой подход к шифрованию.
Особенность шифрования с открытым ключом состоит в том, что одновременно
генерируется уникальная пара ключей, таких что текст, зашифрованный одним ключом,
может быть расшифрован только с использованием второго ключа, и наоборот.
Рис. 3. Модель криптосистемы с открытым ключом

9.

Несимметричные алгоритмы шифрования
В модели криптосхемы с открытым ключом также три участника: отправитель,
получатель и злоумышленник (рис. 3).
Задача отправителя заключается в том, чтобы по открытому каналу связи передать
некоторое сообщение в защищенном виде. Получатель генерирует на своей стороне два
ключа: открытый Е и закрытый D. Закрытый ключ D (часто называемый также личным
ключом) абонент должен сохранять в защищенном месте, а открытый ключ Е он может
передать всем, с кем хочет поддерживать защищенные отношения. Для шифрования текста
служит открытый ключ, но расшифровать этот текст можно только с помощью закрытого
ключа. Поэтому открытый ключ передается отправителю в незащищенном виде.
Отправитель, используя открытый ключ получателя, шифрует сообщение X и
передает его получателю. Получатель расшифровывает сообщение своим закрытым ключом
D. Очевидно, что числа, одно из которых служит для шифрования текста, а другое — для
дешифрирования, не могут быть независимыми друг от друга, а значит, есть теоретическая
возможность вычисления закрытого ключа по открытому. Однако это связано с огромным
объемом вычислений, которые требуют соответственно огромного времени. Поясним
принципиальную связь между закрытым и открытым ключами следующей аналогией.

10.

Несимметричные алгоритмы шифрования – пример-аналогия
Пусть руководитель предприятия (на рис. 4 это пользователь 1) решает вести
секретную переписку со своими сотрудниками. Рассмотрим вариант, когда требуется
обеспечить конфиденциальность потока сообщений только в одну сторону — от сотрудников
к руководителю. Для этого руководитель решает использовать какой-либо малоизвестный
язык, например санскрит. С этой целью он обзаводится единственной копией санскритскорусского словаря, который оставляет себе, и большим количеством широкодоступных русскосанскритских словарей, которые раздает всем своим сотрудникам.
Когда у сотрудников возникает
необходимость написать секретное
сообщение руководителю, они,
пользуясь словарем, пишут сообщения
на санскрите. Руководитель переводит
сообщения на русский язык, пользуясь
доступным только ему санскритскорусским словарем. Очевидно, что здесь
роль открытого ключа Е и закрытого
ключа D руководителя играют русскосанскритский и санскритско-русский
словари соответственно.
Рис. 4. Пример криптосистемы с открытым ключом

11.

Несимметричные алгоритмы шифрования – пример-аналогия
Могут ли пользователи 2, 3 и 4 прочитать чужие сообщения S2, S3, S4, которые
посылает каждый из них руководителю? Вообще-то нет, так как для этого им нужен
санскритско-русский словарь, обладателем которого является только пользователь 1. Так
обеспечивается конфиденциальность потока сообщений в направлении руководителя.
Заметим, что у сотрудников имеется теоретическая возможность для разгадывания
сообщений друг друга, так как, затратив массу времени, можно прямым перебором составить
санскритско-русский словарь по русско-санскритскому. Такая очень трудоемкая процедура,
требующая больших затрат времени, отдаленно напоминает восстановление закрытого
ключа по открытому.

12.

Несимметричные алгоритмы шифрования – пример-аналогия
На рис. 5 показана другая схема использования открытого и закрытого ключей,
целью которой является подтверждение авторства (аутентификация) посылаемого
сообщения. Пусть задача подтверждения авторства ставится только в отношении посланий
руководителя своим сотрудникам. В этом случае роль закрытого (D) и открытого (Е) ключей
руководителя играют русско-санскритский и санскритско-русский словари соответственно,
причем наши предположения о доступности этих словарей меняются на противоположные.
Итак, руководитель пишет письма своим
сотрудникам на санскрите (то есть шифрует
их закрытым ключом D). Сотрудник,
получивший послание, пытается перевести
зашифрованную часть письма, пользуясь
санскритско-русским словарем (открытым
ключом Е). Если ему это удается, то это
доказывает, что текст был зашифрован
закрытым ключом, парным открытому ключу
Е руководителя. А владельцем этого парного
ключа может быть только руководитель,
значит, именно он является автором этого
сообщения.
Сообщения первого пользователя S12, S13, S14,
адресованные пользователям 2, 3 и 4, не являются
секретными, так как все адресаты обладают одним
и тем же открытым ключом, с помощью которого
они могут расшифровывать все сообщения,
поступающие от пользователя 1.
Рис. 5. Использование шифрования закрытым
ключом для подтверждения авторства

13.

Несимметричные алгоритмы шифрования
Для того чтобы в сети все n абонентов имели возможность не только принимать
зашифрованные сообщения, но и сами посылать таковые, каждый абонент должен обладать
собственной парой ключей Е и D. Всего в сети будет 2п ключей: п открытых ключей для
шифрования и n секретных ключей для дешифрирования. Таким образом решается проблема
масштабируемости — квадратичная зависимость количества ключей от числа абонентов в
симметричных алгоритмах заменяется линейной зависимостью в несимметричных
алгоритмах. Решается и проблема секретной доставки ключа. Злоумышленнику нет смысла
стремиться завладеть открытым ключом, поскольку это не дает возможности
расшифровывать текст или вычислить закрытый ключ.
Хотя информация об открытом ключе не является секретной, ее нужно защищать
от подлогов, чтобы злоумышленник под именем легального пользователя не навязал свой
открытый ключ, после чего с помощью своего закрытого ключа он сможет расшифровывать
все сообщения, посылаемые легальному пользователю, и отправлять свои сообщения от его
имени. Проще всего было бы распространять списки, связывающие имена пользователей с их
открытыми ключами, широковещательно путем публикаций в средствах массовой
информации (бюллетени, специализированные журналы и т. п.). Однако при таком подходе
мы снова, как и в случае с паролями, сталкиваемся с плохой масштабируемостью. Решением
проблемы является технология цифровых сертификатов — электронных документов, которые
связывают конкретных пользователей с конкретными открытыми ключами.

14.

Алгоритм RSA
В настоящее время одним из наиболее популярных криптоалгоритмов с открытым
ключом является криптоалгоритм RSA.
В 1978 году трое ученых (Ривест, Шамир и Адлеман) разработали систему
шифрования с открытыми ключами RSA (Rivest, Shamir, Adleman), полностью отвечающую
всем принципам Диффи—Хеллмана. Этот метод состоит в следующем.
1. Случайно выбираются два очень больших простых числа p и q.
2. Вычисляются два произведения n = р х q и m = (р - 1) х (q - 1).
3. Выбирается случайное целое число Е, не имеющее общих сомножителей c m.
4. Находится D такое, что DE = 1 по модулю m.
5. Исходный текст X разбивается на блоки таким образом, чтобы 0 < Х< п.
E
6. Для шифрования сообщения необходимо вычислить С X по модулю п.
7. Для дешифрирования вычисляется X = С D по модулю п.
Таким образом, чтобы зашифровать сообщение, необходимо знать пару чисел (E,
n), а чтобы расшифровать — пару чисел (D, п). Первая пара — это открытый ключ, а вторая
— закрытый.
Зная открытый ключ (E, n), можно вычислить значение закрытого ключа D.
Необходимым промежуточным действием в этом преобразовании является нахождение чисел
р и q, для чего нужно разложить на простые множители очень большое число я, а на это
требуется очень много времени. Именно с огромной вычислительной сложностью
разложения большого числа на простые множители связана высокая криптостойкость
алгоритма RSA.

15.

Алгоритм RSA
В некоторых публикациях приводятся следующие оценки: для того чтобы найти
разложение 200-значного числа, понадобится 4 миллиарда лет работы компьютера с
быстродействием миллион операций в секунду. Однако следует учесть, что в настоящее
время активно ведутся работы по совершенствованию методов разложения больших чисел,
поэтому в алгоритме RSA стараются применять числа длиной более 200 десятичных
разрядов.
Программная реализация криптоалгоритмов типа RSA значительно сложнее и
менее производительна, чем реализации классических криптоалгоритмов тина DES.
Вследствие сложности реализации операций модульной арифметики криптоалгоритм RSA
обычно используют только для шифрования небольших объемов информации, например для
рассылки классических секретных ключей или в алгоритмах цифровой подписи, а основную
часть пересылаемой информации шифруют с помощью симметричных алгоритмов.
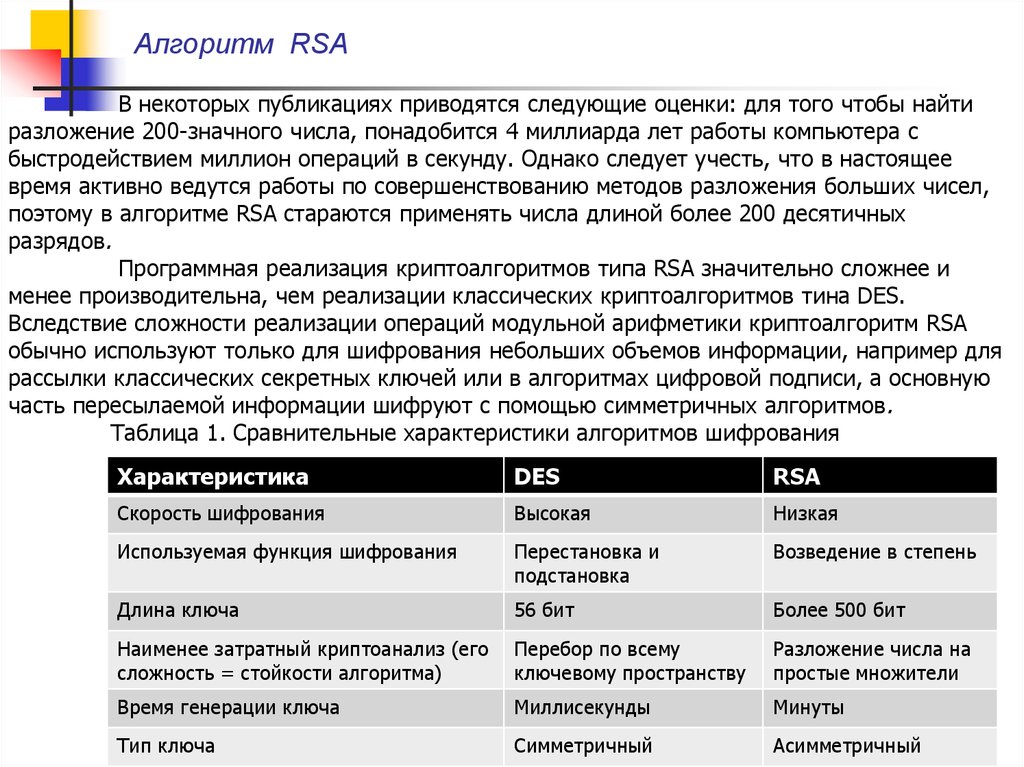
Таблица 1. Сравнительные характеристики алгоритмов шифрования
Характеристика
DES
RSA
Скорость шифрования
Высокая
Низкая
Используемая функция шифрования
Перестановка и
подстановка
Возведение в степень
Длина ключа
56 бит
Более 500 бит
Наименее затратный криптоанализ (его
сложность = стойкости алгоритма)
Перебор по всему
ключевому пространству
Разложение числа на
простые множители
Время генерации ключа
Миллисекунды
Минуты
Тип ключа
Симметричный
Асимметричный

16.

Односторонние функции шифрования
Во многих базовых технологиях безопасности используется еще один прием
шифрования — шифрование с помощью односторонней функции (one-way function),
называемой также необратимой функцией, хэш-функцией (hash function) или
дайджест-функцией (digest function).
Эта функция, примененная к шифруемым данным, дает в результате значение,
называемое дайджестом, которое состоит из фиксированного сравнительно небольшого и
не зависящего от длины шифруемого текста числа байтов.
Подчеркнем, знание дайджеста не позволяет и даже не предполагает
восстановления исходных данных. Для чего же нужны односторонние функции шифрования
(ОФШ)?
Для ответа на этот вопрос рассмотрим несколько примеров. Пусть требуется
обеспечить целостность сообщения, передаваемого по сети. Отправитель и получатель
договорились, какую ОФШ и с каким значением параметра — секретного ключа — они будут
использовать для решения этой задачи.

17.

Односторонние функции шифрования
Прежде чем отправить сообщение, отправитель вычисляет для него дайджест и
отправляет его вместе с сообщением адресату (рис. 6, а). Адресат, получив данные,
применяет ОФШ к переданному в открытом виде исходному сообщению. Если значения
вычисленного локально и полученного по сети дайджестов совпадают, значит, содержимое
сообщения не было изменено во время передачи.
Таким образом, хотя знание
дайджеста не дает возможности
восстановить исходное сообщение,
оно позволяет проверить целостность
данных.
На первый взгляд кажется, что
дайджест является своего рода
контрольной суммой для исходного
сообщения. Однако имеется и
существенное отличие. Контрольные
суммы применяются тогда, когда
нужно обнаружить ошибки,
вызванные техническими
неполадками, например помехами в
линии связи.
Рис. 6. Использование односторонних функций
шифрования для контроля целостности

18.

Односторонние функции шифрования
Это средство не распознает модификацию данных злоумышленником, который,
подменив сообщение, может просто добавить к нему заново вычисленную контрольную
сумму.
В отличие от контрольной суммы дайджест вычисляется с использованием
параметра — секретного ключа. Поскольку значение секретного ключа для ОФШ известно
только отправителю и получателю. Любая модификация исходного сообщения будет
немедленно обнаружена.
На рис. 1, б показан другой вариант
использования односторонней
функции шифрования для
обеспечения целостности данных.
Здесь односторонняя функция не
имеет параметра-ключа, но зато
применяется не просто к сообщению,
а к сообщению, дополненному
секретным ключом. Получатель
извлекает из полученных по сети
данных исходное сообщение, потом
дополняет его тем же известным ему
секретным ключом и применяет к
полученным данным одностороннюю
функцию. Результат вычислений
сравнивается с полученным по сети
дайджестом.

19.

Односторонние функции шифрования
Помимо обеспечения целостности сообщений, дайджест может быть использован в
качестве электронной подписи для аутентификации передаваемого документа.
Построение односторонних функций является трудной задачей. Такого рода
функции должны удовлетворять двум условиям:
по дайджесту, вычисленному с помощью данной функции, должно быть
невозможно каким-либо образом вычислить исходное сообщение;
должна отсутствовать возможность вычисления двух разных сообщений, для
которых с помощью данной функции могли быть вычислены одинаковые
дайджесты.
Наиболее популярной в системах безопасности в настоящее время является серия
хэш-функций MD2, MD4, MD5. Все они генерируют дайджесты фиксированной длины 16 байт.
Адаптированным вариантом MD4 является американский стандарт SHA, длина дайджеста в
котором составляет 20 байт. Компания IBM поддерживает односторонние функции MDC2 и
MDC4, основанные на алгоритме шифрования DES.

20.

Дополнительные материалы для изучения
История криптографии
Проблема сокрытия содержания послания при его транспортировке волновала
людей с древних пор. Достаточно давно были использованы методы стеганографии, когда
на выбритой голове писался текст послания, затем ждали, когда отрастут волосы, и посланец
отправлялся в путь. По прибытии голову снова брили и сообщение читалось. В 21-ом веке
метод стеганографии неожиданно получил новое развитие. Оказалось, что в графическом
файле можно пересылать сообщения и изображения, даже факт наличия которых трудно
установить. Смотри History of Cryptography.
Известно, что еще Цезарь (100-44 годы до нашей эры) при переписке использовал
шифр, получивший его имя. В 1518 году Джоанес Тритемиус написал первую книгу по
криптографии, где впервые были описаны многоалфавитные подстановочные шифры. Лишь в
1918 году во время первой мировой войны в Германии была применена шифровальная
система ADFGVX. Позднее в 1933-45 годах в Германии была разработана и применена первая
шифровальная машина Enigma (на этом принципе работает система crypt в UNIX). Мощное
развитие криптография получила в период второй мировой войны. С этой шифровальной
машиной связан и первый успех в области вскрытия сложных шифров. В 19-ом веке голандец
Август Керкхоф сформулировал фундаментальное требование, предъявляемое к
криптосистемам и сегодня (принцип Керкхофа):
Секретность шифра должна базироваться не на секретности алгоритма, а на
секретном ключе.
Если в алгоритм заложена возможность относительно быстрого дешифрования
(мечта всех спецслужб мира), то рано или поздно это станет известно, и такой возможностью
воспользуются злоумышленники, что может привести к утечке критическо важной
информации. Основы современной криптографии были заложены в работе Клода Шеннона
“Теория связи в секретных системах” (1949).

21.

Дополнительные материалы для изучения
История криптографии
Чаще всего шифруются тексты документов, но в последнее время шифрованию
подвергаются и изображения, голосовые данные и даже тексты программ.
Во время второй мировой войны в Великобритании в Government Code and Cypher
School работало более 10000 человек (из них две трети женщин). Код немецкой
шифровальной машины Энигма взломал английский математик Алан Тьюринг, но в той или
иной степени в этом участвовали и остальные 10000 сотрудников. Ключи настройки машины
Энигма изменялись каждые сутки в полночь. В результате были дешифрованы два с
половиной миллиона нацистских секретных сообщений. Следует иметь в виду, что тогда не
было ЭВМ в современном понимании этого слова и вся работа выполнялась с помощью
электромеханических устройств (Colossus - British Tabulating Machine Company). Англичане
считают эту машину первым программируемым электронным компьютером. Если бы эти
сообщения дешифровались в ручную, то надо было бы перебрать 158x1018 вариантов.
Colossus эмулировал работу 36 машин Энигма. Многие сообщения начинались с
метеорологических данных, что позволяло проверить настройки дешифровальной машины.
Сотрудники, обслуживающие Colossus, работали парами, чтобы исключить случайные
ошибочные действия. Работа была посменная, круглосуточная. Работа проходила в условиях
глубокой секретности. Более поздняя версия Mark II Colossus была способна дешифровать до
25000 символов в секунду. Машина Colossus поддерживается в рабочем состоянии и сегодня,
но уже в качестве музейного экспоната.
Шифрование предполагает преобразование исходного текста Т с использованием
ключа К в зашифрованный текст t. Симметричные криптосистемы для шифрования и
дешифрования используется один и тот же ключ К. Появившиеся в последние годы системы
с открытым ключом, осуществляют шифрование с помощью общедоступного ключа, для
дешифрования в этом случае необходим секретный ключ, который порождается совместно с

22.

Дополнительные материалы для изучения
Общие требования к криптосистемам
Знание использованного алгоритма не должно снижать надежность
шифрования.
Длина зашифрованного текста должна быть равна длине исходного открытого
текста (это требование относится к числу желательных и выполняется не
всегда).
Зашифрованный текст не может быть прочтен без знания ключа.
Каждый ключ из многообразия ключей должен обеспечивать достаточную
надежность.
Изменение длины ключа не должно приводить к изменению алгоритма
шифрования.
Если известен зашифрованный и открытый текст сообщения, то число операций,
необходимых для определения ключа, не должно быть меньше полного числа
возможных ключей.
Дешифрование путем перебора всех возможных ключей должно выходить
далеко за пределы возможностей современных ЭВМ.
Если при шифровании в текст вводятся дополнительные биты, то алгоритм их
внесения должен быть надежно скрыт.
Не должно быть легко устанавливаемой зависимости между последовательно
используемыми ключами.
Алгоритм может быть реализован аппаратно.
В симметричных криптосистемах могут использоваться одно- или многоалфавитные
подстановки (например, одно-алфавитная подстановка Цезаря), при этом производится
замена символов исходного текста на другие с использованием достаточно сложных
алгоритмов.

23.

Дополнительные материалы для изучения
Общие требования к криптосистемам
Многоалфавитные подстановки несравненно более надежны. К числу простых
методов шифрования относится способ перестановок символов исходного текста (этот метод
эффективен только лишь при достаточно большой длине исходного текста). Множество
перестановок символов для текста из N символов равно N!, что до какой-то степени
гарантирует надежность процедуры. Несколько большую надежность предлагает метод
гаммирования, когда на исходный текст накладывается псевдослучайная последовательность
бит, генерируемая на основе ключа шифрования, например, с использованием операции
исключающего ИЛИ. Обратное преобразование (дешифрование) выполняется генерацией
точно такой же псевдослучайной последовательности и наложением ее на зашифрованной
текст. Гаммирование уязвимо для случая, когда злоумышленнику становится известен
фрагмент исходного текста. В этих обстоятельствах он без труда восстановит фрагмент
псевдослучайной последовательности, а по нему и всю последовательность. Так если
достаточно большое число сообщений начинается со слов "Секретно", а в конце ставится
дата сообщения, расшифровка становится вопросом времени и терпения.
Ключ может быть одноразового и многоразового использования. Одноразовый
ключ достаточно большой длины (или бесконечный) может обеспечить сколь угодно высокую
надежность, но его использование создает неудобства, связанные с его транспортировкой
(ключ должен быть как-то доставлен получателю зашифрованного послания).

24.

Дополнительные материалы для изучения
Общие требования к криптосистемам
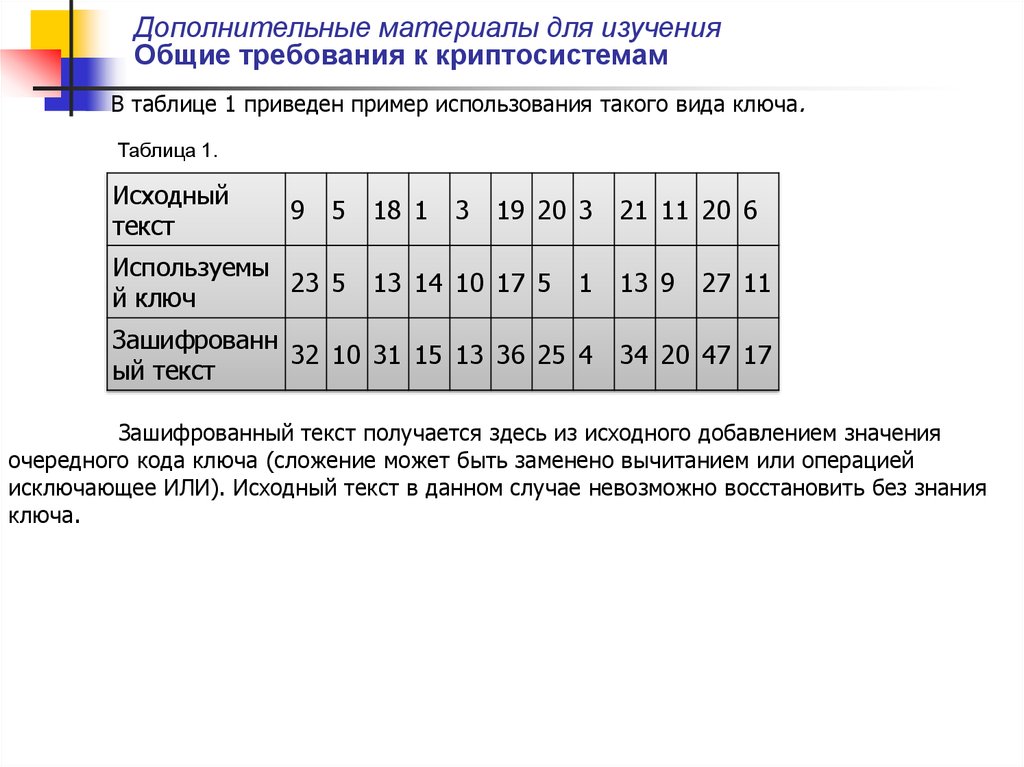
В таблице 1 приведен пример использования такого вида ключа.
Таблица 1.
Исходный
текст
9
5
Используемы
23 5
й ключ
18 1
3
19 20 3
13 14 10 17 5
1
Зашифрованн
32 10 31 15 13 36 25 4
ый текст
21 11 20 6
13 9
27 11
34 20 47 17
Зашифрованный текст получается здесь из исходного добавлением значения
очередного кода ключа (сложение может быть заменено вычитанием или операцией
исключающее ИЛИ). Исходный текст в данном случае невозможно восстановить без знания
ключа.

25.

Дополнительные материалы для изучения
Общие требования к криптосистемам
Примером шифрования с использованием секретного ключа является метод
Видженера (Vigenere; www.massconfusion.com/crypto/lecture/method6.shtml), относящийся к
числу много алфавитных подстановок. Здесь берется небольшое целое число m и алфавит
после каждой символьной подстановки сдвигается на m символов. Например, для m=4.
1. abcdefghijklmnopqrstuvwxyz
ghijklmnopqrstuvwxyzabcdef
2. opqrstuvwxyzabcdefghijklmn
3. Lmnopqrstuvwxyzabcdefghijk
4. fghijklmnopqrstuvwxyzabcde
Ключ = golf (смотри левую вертикальную колонку символов).
Исходный текст разбивается на группы по m символов (в рассмотренном случае по
4). Для каждой группы первый символ заменяется соответствующей буквой первого
алфавита, вторая - из второго и т.д. Например, фраза "get me out of here please" будет
преобразована следующим образом:
getm eout ofhe repl ease
mser kcfy utsj xsaq kohj

26.

Дополнительные материалы для изучения
Система DES
Наибольшее распространение в последнее время получило блочное шифрование,
где последовательность процедур воздействует на блок входного текста. Одним из наиболее
известных таких методов стал DES (Data Encryption Standard), который работает с блоками
данных по 64 байта (1998 год). Существует четыре режима работы:
ECB electronic code book;
CBC cipher block chaining;
CFB cipher feedback;
OFB output feedback.
Из-за того, что алгоритм DES в настоящее время представляется устаревшим и не
обеспечивает достаточной надежности, довольно часто исходный текст последовательно
шифруется трижды с помощью различных ключей.
Шифрование и дешифрование базируются на использовании ключей.
Математически это можно выразить следующим образом (cм.
lglwww.epfl.ch/~jkienzle/digital_money/node11.html;
www.ee.mtu.edu/courses/ ee465/groupa/overview.html):
EK(M) = C
DK(c) = M, где K – секретный ключ, M - исходный текст; C - зашифрованный текст; Е –
алгоритм шифрования; D – алгоритм дешифрования.
Эффективность системы шифрования определяется числом кодовых комбинаций
или ключей, которое необходимо перебрать, чтобы прочесть зашифрованный текст.
Существует две системы ключей шифрования/дешифрования. Для симметричных алгоритмов
предполагается, что ключ дешифрования может быть вычислен по известному ключу
шифрования. Оба ключа при этом должны быть секретными (например, система DES).

27.

Дополнительные материалы для изучения
Система DES
Отправитель и получатель должны знать ключи до начала обмена (эти ключи могут
и совпадать). Набор таких ключей может быть достаточно большим и в процессе
инициализации осуществляется выбор пары ключей, которые будут использованы в данной
сессии. В общем случае могут использоваться довольно большие кодовые таблицы, но такая
схема неудобна для многоточечного обмена.
Шифры бывают поточными и блочными. В первом случае обработка исходного
текста производится побитно или побайтно. Во втором - текст перед обработкой разбивается
на блоки.
Асимметричные схемы шифрования/дешифрования предполагают существования
независимых ключей для шифрования и дешифрования. Причем один не может быть получен
из другого и наоборот. В идеале ключ дешифровки не может быть получен из шифрующего
ключа за любое разумное время. В этом случае ключ шифрования может быть сделан
общедоступным (например, алгоритм RSA). Партнеры до начала коммуникаций должны
послать друг другу ключи шифрования КШО и КШП (ключи шифрования отправителя и
получателя). Возможность перехвата таких ключей опасности не представляет.
Дешифрование выполняется с помощью ключей КДО и КДП, которые образуют пары с КШО и
КШП соответственно и формируются совместно. Ключи КШО и КШП обычно пересылаются на
фазе инициализации сессии информационного обмена.
Шифрование может осуществляться по определенным правилам с помощью таблиц
шифрования или ключей. При этом могут использоваться самые разные алгоритмы, в том
числе, например, перемещение символов текста определенным образом. За свою историю
люди придумали достаточно большое число способов шифрования. Новейшие из них
базируются на методиках, заимствованных из теории чисел. По этой причине, прежде чем
переходить к следующему разделу, введем некоторые определения.

28.

Дополнительные материалы для изучения
Базовые определения и теоремы
Конгруентность. a конгруентно b по модулю n (a ≡ nb), если при делении на n a и
b, получается идентичный остаток. Так 100 ≡ 1134 (100 и 34 при делении на 11 дают остаток
1) и -6 ≡ 810 (ведь -6 =8(-1)+2). Мы всегда имеем a ≡ nb для некоторого 0 ≤ b≤ n-1. Если a
≡ nb и с ≡ d, то справедливы равенства:
a +c ≡ n(b + d) и ac ≡ nbd
Аналогичная процедура для деления не всегда справедлива: 6 ≡ 1218 но 3 ≠ 9.
Приведенные здесь и далее математические определения и обоснования взяты из:
http://lglwww.epfl.ch/~jkienzle/digital/node20.html.
Необходимо также вспомнить о знакомом всем со школьной скамьи понятии
наибольшего общего делителя. Для a и b число (a,b) является наибольшим общим
делителем, который делит a и b без остатка: (56,98)=14; (76,190)=38.
Теорема 1. Для любых a,b существуют целые числа x,y, для которых
ax+by=(a,b). В данной статье не приводится доказательств представленных утверждений,
их следует искать в книгах по дискретной математике.
В этом можно убедиться, решая уравнение 30x+69y=3 путем последовательных
упрощающих подстановок (ищется целочисленное решение: 30x+69y=3)
30x'+9y=3
[x'=x+2y]
3x'+9y'=3
[y'=y+3x']
3x"+0y'=3
[x"=x'+3y'].
Легко видеть, что x"=1, y'=0 является решением окончательного уравнения. Мы
можем получить решение исходного уравнения путем обратной подстановки
x'=x"-3y'=1; y=y'-3x'=-3; x=x'-1y=7.
Мы можем решить уравнение вида 30x+69y=15 путем умножения нашего решения: y=-15,
x=35.

29.

Дополнительные материалы для изучения
Базовые определения и теоремы
Должно быть ясно, что уравнение не будет иметь целочисленного решения, если 15
заменить на что-то некратное (30,69)=3.
Все другие целочисленные решения 30x+69y=15 могут быть получены, варьируя
первое решение:
y=-15+(30/3)t x=35 -(69/3)t для целого t.
Если мы проделаем то же для произвольного равенства ax+by=(a,b), мы
возможно получим один из коэффициентов равным нулю, а другой - (a,b). В
действительности эта процедура представляет собой алгоритм Евклида для нахождения
наибольшего общего делителя.
Важно то, что этот процесс реализуем на ЭВМ даже в случае, когда a и b имеют
несколько сотен значащих цифр. Легко показать, что 600-значное число не потребует более
чем 4000 уравнений. Теорема 1 справедлива и для простых чисел.
Следствие 1. Если p является простым числом, ar ≡ pas и a ≠ 0, тогда r ≡ s.
Следствие 2. Если p простое число и a ≠ 0 mod p, тогда для любого b существует y, для
которого ay ≡ pb.
Следствие 3. ("Теорема о китайском остатке"). Если (p,q)=1, тогда для любого a,b
существует n, для которого n ≡ pa и n≡ qb.
Во многих криптографических приложениях используется:
a a2 a3 … mod p, где a и p целые числа.
Оказывается, можно выполнить такие вычисления даже для случая, когда в
указанную процедуру вовлечены достаточно большие числа, например:
432678 mod 987.

30.

Дополнительные материалы для изучения
Базовые определения и теоремы
квадрат.
Фокус заключается в том, что берется число и осуществляется возведение в
4322 = 186624; 186624 mod 987 = 81; 4324 mod 987 = 812 mod 987 = 639
4328 -> 6392 mod 987 -> 690 …. 432512 -> 858
так как 678= 512+128+32+4+2, то:
432678->(81)(639)….(858) -> 204
Вычисления с использованием показателя включают в себя ограниченное число
умножений. Если числа содержат несколько сотен цифр, необходимы специальные
подпрограммы для выполнения таких вычислений. Рассмотрим последовательность степеней
2n mod 11:
2 4 8 5 10 9 7 3 6 1
Здесь числа от 1 до 10 появляются в виде псевдослучайной последовательности.
Теорема 2
Пусть p является простым числом. Существует такое a, что для каждого 1≤ b ≤ p1, существует такое 1≤ x ≤ p-1, что ax ≡ pb, a не обязательно равно 2.
Степени 2 mod 7 равны 2, 4, 1. Далее числа повторяются, а числа 3, 5, или 6 не
могут быть получены никогда. Рассмотрим некоторые следствия этой теоремы.
Следствие 4. Пусть a соответствует требованиям теоремы 2, тогда ap-1 ≡ p1.
Следствие 5. Для любого b ≠ 0, bp-1 ≡ p1.
Следствие 6. Если x ≡ (p-1)y, тогда bx ≡ pby
Лемма
Пусть b ≠ 0, d наименьшее положительное число, такое что bd ≡ p1. Тогда для любого с>0
c bc ≡ p1 d делит c без остатка. В частности для следствия 5, d делит p-1 без остатка.

31.

Дополнительные материалы для изучения
Базовые определения и теоремы
Согласно теореме 2, если p простое число, существует такое a, при котором
равенство ax ≡ pb имеет решение для любого b ≠ 0. Такое значение a называется
примитивным корнем p, а x называется дискретным логарифмом b. Получение b при
заданных a и x относительно просто, определение же x по a и b заметно сложнее. Многие
современные системы шифрования основываются на факте, что никаких эффективных путей
вычисления дискретных логарифмов не найдено. Никакого эффективного метода
определения примитивных корней также неизвестно. Однако часто возможно найти
примитивные корни в некоторых специальных случаях. Возьмем p=1223. p-1=2*13*47.
Согласно лемме, если a не примитивный корень, тогда мы либо имеем a26, a94 или
a611 ≡ 12231. a=2 и a=3 не годятся, но a=5 соответствует всем трем условиям, таким
образом, это значение является примитивным корнем. Мы могли бы сказать, что a=4 не
может быть признано примитивным корнем без проверки.
Легко показать, что если a примитивный корень, ax примитивный корень в том и
только том случае, если (x,p-1)=1. В этом примере это означает, что число примитивных
корней равно
1222*(1/2)*(12/13)*(46/47)=552.
Таким образом, если мы выберем а произвольно, вероятность того, что это будет
примитивный корень равна ~.45. Выбирая а наугад и тестируя, можно сравнительно быстро
найти примитивный корень.
Наиболее современные системы шифрования используют асимметричные
алгоритмы с открытым и секретным ключами, где нет проблемы безопасной транспортировки
ключа. К числу таких систем относится алгоритм rsa (rivest-shamir-adleman - разработчики
этой системы - Рональд Ривест, Ади Шамир и Леонард Адлеман, 1977 год), базирующийся на
разложение больших чисел на множители.

32.

Дополнительные материалы для изучения
Базовые определения и теоремы
Другие сходные алгоритмы используют целочисленные логарифмы, элиптические
кривые (считается одним из наиболее криптографически прочных) и вычисление корней
уравнений. В отличие от других систем эти позволяют кроме шифрования эффективно
идентифицировать отправителя (электронная подпись). К системам с открытым ключом
предъявляются следующие требования:
шифрованный текст трудно (практически невозможно) расшифровать с
использованием открытого ключа.
установление закрытого ключа на основе известного открытого должно быть
нереализуемой задачей на современных ЭВМ. При этом должна существовать
объективная оценка нижнего предела числа операций, необходимых для
решения такой задачи.
К сожалению, эти алгоритмы достаточно медленно работают. По этой причине они
могут использоваться для транспортировки секретных ключей при одном из традиционных
методов шифрования-дешифрования.
Но следует помнить, что не существует абсолютных мер защиты. На рис. 7. показан
способ нарушения конфиденциальности в системах с двухключевой схемой шифрования.
Рис. 7.

33.

Дополнительные материалы для изучения
Базовые определения и теоремы
Если хакер умудрится вставить свою ЭВМ в разрыв канала, соединяющего
субъектов А и В, у него появляется возможность перехватывать в том числе и шифрованные
сообщения. Пусть субъект А сформировал пару ключей К1А и К2А (ключ с индексом 2
является секретным), аналогичную пару ключей сгенерировал субъект В (К1В и К2В). Хакер
же тем временем подготовил две пары ключей (К1ХА:К2ХА и К1ХВ:К2ХВ). Когда субъект А
пошлет открытый ключ К1А субъекту В, хакер его подменит ключом К1ХА. Аналогичную
процедуру он проделает с ключом К1В, посланным от В к А. Теперь сообщение А к В,
зашифрованное с помощью ключа К1ХА будет послано В. Хакер его перехватывает,
дешифрует с помощью ключа К2ХА, шифрует с помощью ключа К1ХВ и посылает В. Субъект В,
получив послание, дешифрует его с помощью "секретного" ключа К2ХВ, полученного от
хакера (о чем он, естественно, не подозревает). Аналогичная процедура будет проведена и
при посылки сообщения от В к А. В сущности единственным параметром который изменится
существенным образом будет время доставки сообщения, так как это время будет включать
дешифровку и повторную шифровку сообщения. Но при использовании быстродействующей
ЭВМ и при работе с традиционной электронной почтой это может оказаться незаметным.
Понятно, что между А и В появится дополнительный шаг (hop). Но и это может быть легко
замаскировано под прокси сервер или Firewall.

34.

Дополнительные материалы для изучения
Базовые определения и теоремы
Решить эту проблему подмены ключей можно путем пересылки открытого ключа
своему партнеру по какому-то альтернативному каналу или сверки его по телефону.
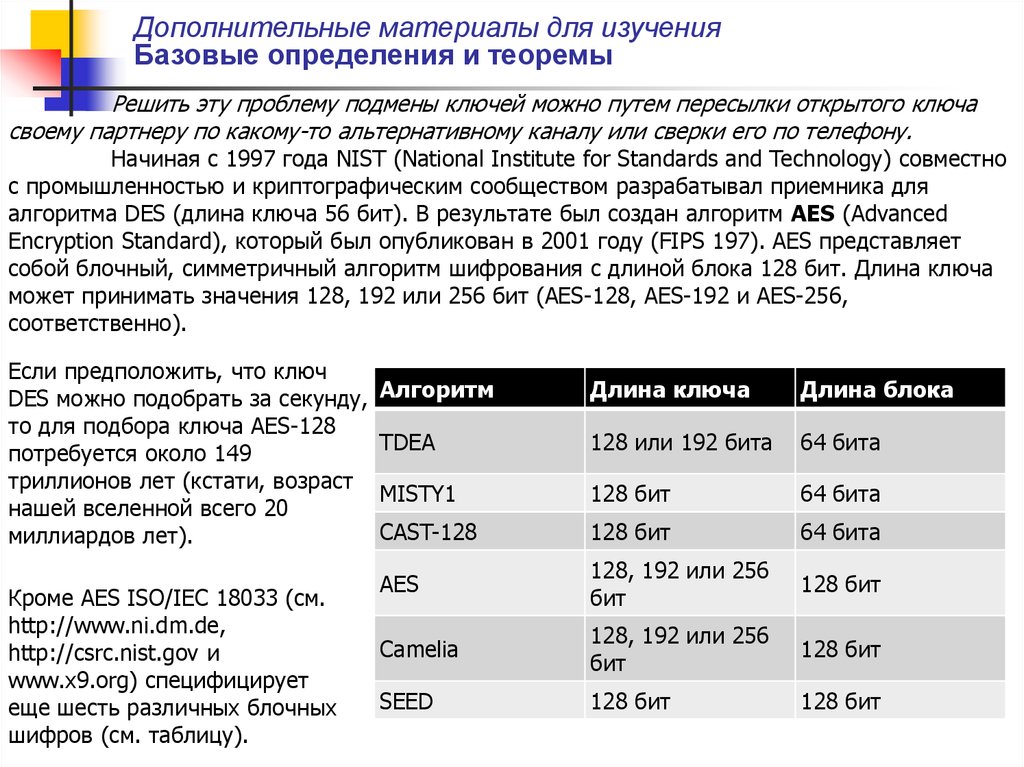
Начиная с 1997 года NIST (National Institute for Standards and Technology) совместно
с промышленностью и криптографическим сообществом разрабатывал приемника для
алгоритма DES (длина ключа 56 бит). В результате был создан алгоритм AES (Advanced
Encryption Standard), который был опубликован в 2001 году (FIPS 197). AES представляет
собой блочный, симметричный алгоритм шифрования с длиной блока 128 бит. Длина ключа
может принимать значения 128, 192 или 256 бит (AES-128, AES-192 и AES-256,
соответственно).
Если предположить, что ключ
DES можно подобрать за секунду,
то для подбора ключа AES-128
потребуется около 149
триллионов лет (кстати, возраст
нашей вселенной всего 20
миллиардов лет).
Кроме AES ISO/IEC 18033 (см.
http://www.ni.dm.de,
http://csrc.nist.gov и
www.x9.org) специфицирует
еще шесть различных блочных
шифров (см. таблицу).
Алгоритм
Длина ключа
Длина блока
TDEA
128 или 192 бита
64 бита
MISTY1
128 бит
64 бита
CAST-128
128 бит
64 бита
AES
128, 192 или 256
бит
128 бит
Camelia
128, 192 или 256
бит
128 бит
SEED
128 бит
128 бит

35.

Дополнительные материалы для изучения
Базовые определения и теоремы
Базовые характеристики блочных алгоритмов шифрования представлены в таблице
ниже (смотри http://book.itep.ru/6/idea_647.htm, ~6/des_641.htm и ~6/safr_648.htm).
Алгоритм
Размер блока данных
Длина ключа
DES
64
56
ГОСТ 28147-89
64
256
SAFER+
128
128/192/256
IDEA
64
52*16
Относительные уровни безопасности разных алгоритмов представлены ниже.
Симметричный
шифр
Хэш функция Схема RSA
Эллиптические
кривые
56 (DES)
112
512
112
80 (SKIPJACK)
160 (RIPEMD160)
1024
160
112 (Triple-DES)
224
2048
224
128 (AES-128)
256 (SHA-256)
3072
256
192 (AES-192)
384 (SFA-384)
7680
384
256 (AES-256)
512 (SFA-512)
15360
512

36.

Дополнительные материалы для изучения
Базовые определения и теоремы
Стандарт на хэш функции задает документ ISO/IEC 10118. К сожалению, не
существует международного стандарта для управления информационными системами
безопасности. Эти хэш функции (см. табл. ниже) используются практически во всех видах
электронных подписей (ISO/IEC 14888). К сожалению, не существует международного
стандарта для управления информационными системами безопасности.
Алгоритм
Соответствующий стандарт
MD5
RFC-1321
SHA-1
FIPS 180-2; ISO/IEC 10118-3RFC3174,
ANSI X9.30.2
RIPEMD-128/-160
ISI/IEC 10118-3
SHA-256/384/512
FIPS 180-2; ISO/IEC 10118-3
Whirlpool
ISO/IEC 10118-3
ГОСТ Р 34.11-94
Предназначен для электронной
подписи ГОСТ Р 34.10-2001

37.

Дополнительные материалы для изучения
Базовые определения и теоремы
В настоящее время имеется три семейства криптосистем с открытым ключом.
1. Системы IF (Integer Factorization - целочисленная факторизация), такие как система
цифровой подписи, базирующаяся на RSA, использует сложность факторизации при
работе с большими целыми числами.
2. Системы DL (Discrete Logarithm - целочисленный логарифм), такие как алгоритм
цифровой подписи NIST (DSA, FIPS 186), базируются на вычислительной сложности
оперирования с целочисленными логарифмами.
3. Системы EC (Elliptic Curve эллиптические кривые) являются сходными с DL примитивами.
Они основываются на вычислительной сложности проблемы расчета целочисленных
логарифмов через эллиптические кривые. Преимуществом этой системы является
относительная ее сила по отношению к длине параметра. Другими словами
эллиптические кривые предоставляют большую секретность на бит. Примером
эллиптической кривой является уравнение типа Y2=X3 +aX+b.
Прочность всех этих алгоритмов основывается на трудностях, например,
разложения больших чисел на сомножители или работы с целочисленными логарифмами. До
сих пор не доказано, что не существует алгоритмов быстрого решения указанных проблем.
Если такие алгоритмы будут найдены, придется придумывать другие системы шифрования.
Следует также помнить, что в случае взлома машины, криптографические методы окажутся
бесполезными, так как, например spyware, сможет иметь доступ к исходному тексту файлов
или вводимых паролей.
Согласно закону Мура число компонентов на чип удваивается каждые 18 месяцев.
Это можно интерпретировать как удвоение вычислительной мощности ЭВМ каждые 18
месяцев.

38.

Дополнительные материалы для изучения
Базовые определения и теоремы
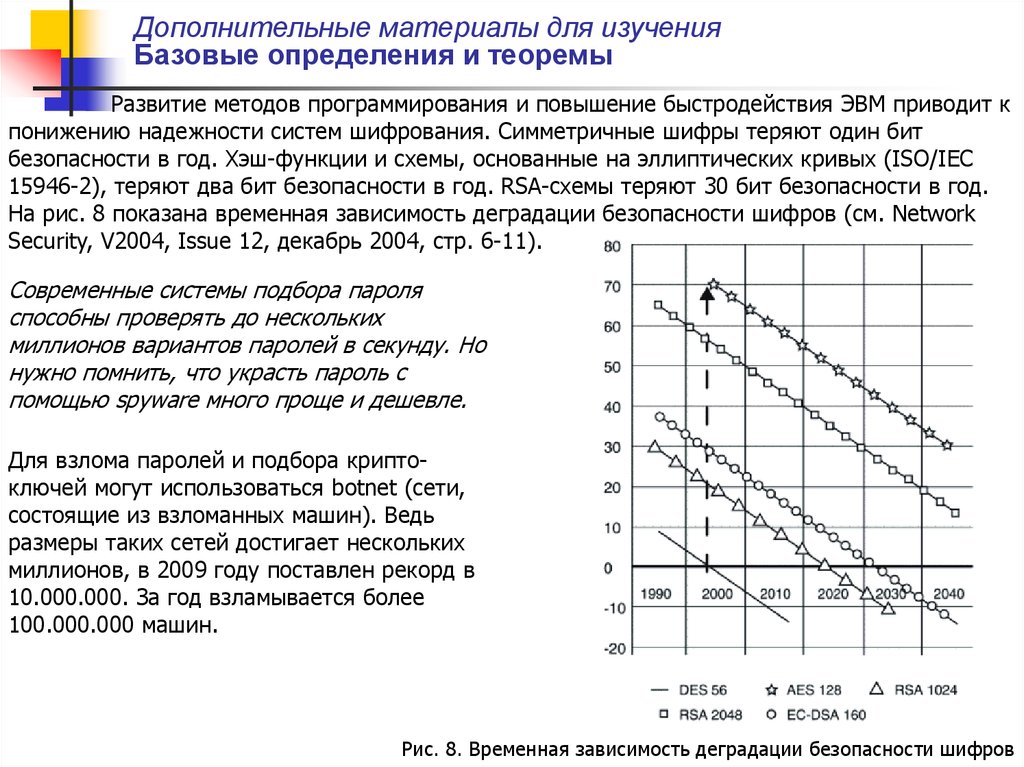
Развитие методов программирования и повышение быстродействия ЭВМ приводит к
понижению надежности систем шифрования. Симметричные шифры теряют один бит
безопасности в год. Хэш-функции и схемы, основанные на эллиптических кривых (ISO/IEC
15946-2), теряют два бит безопасности в год. RSA-схемы теряют 30 бит безопасности в год.
На рис. 8 показана временная зависимость деградации безопасности шифров (см. Network
Security, V2004, Issue 12, декабрь 2004, стр. 6-11).
Современные системы подбора пароля
способны проверять до нескольких
миллионов вариантов паролей в секунду. Но
нужно помнить, что украсть пароль с
помощью spyware много проще и дешевле.
Для взлома паролей и подбора криптоключей могут использоваться botnet (сети,
состоящие из взломанных машин). Ведь
размеры таких сетей достигает нескольких
миллионов, в 2009 году поставлен рекорд в
10.000.000. За год взламывается более
100.000.000 машин.
Рис. 8. Временная зависимость деградации безопасности шифров

39.

Дополнительные материалы для изучения
Базовые определения и теоремы
Полезную информацию по системам шифрования можно получить на следующих серверах:
www.cs.hut.fi/crypto/
www.subject.com/crypto/crypto.html
www.rsa.com/
www.netscape.com/newsref/ref/rsa.html
www.microsoft.com/workshop/prog/security/pkcb/crypt.htm
www.semper.org/sirene/people/gerrit/secprod.html
www.fri.com/~rcv/deschall.htm
www.cl.cam.ac.uk/brute/

40.

Дополнительные материалы для изучения
Алгоритм DES
Стандарт шифрования DES (Data Encryption Standard) был разработан в 1975 году
компанией IBM, он базируется на алгоритме DEA. Исходные идеи алгоритма шифрования
данных DEA (data encryption algorithm) были предложены компанией IBM еще в 1960-х годах
и базировались на идеях, описанных Клодом Шенноном в 1940-х годах. Первоначально эта
методика шифрования называлась lucifer (разработчик Хорст Фейштель, название dea (см.
http//:snoopy.falkor.gen.nz/~rae/des.html) она получила лишь в 1976 году. Lucifer был первым
блочным алгоритмом шифрования, он использовал блоки размером 128 бит и 128-битовый
ключ. По существу этот алгоритм являлся прототипом DEA. В 1986 в Японии (NIT) разработан
алгоритм FEAL(Fast data Encipherment ALgorithm), предназначенный для использования в
факсах, модемах и телефонах (длина ключа до 128 бит). Существует и ряд других
разработок.
DEA (ANSI x3.92-1981; www.cryptosoft.com/html/fips46-2.htm) оперирует с блоками
данных размером 64 бита и использует ключ длиной 56 бит. Такая длина ключа
соответствует 1017 комбинаций, что обеспечивало до недавнего времени достаточный
уровень безопасности. В дальнейшем можно ожидать расширения ключа до 64 бит
(например, LOKI) или вообще замены DES другим стандартом.
Входной блок данных, состоящий из 64 бит, преобразуется в выходной блок
идентичной длины. Ключ шифрования должен быть известен, как отправляющей так и
принимающей сторонам. В алгоритме широко используются перестановки битов текста.

41.

Дополнительные материалы для изучения
Алгоритм DES
Вводится функция f, которая работает с 32-разрядными словами исходного текста
(А) и использует в качестве параметра 48-разрядный ключ (J). Схеме работы функции f
показана на рис. 9. Сначала 32 входные разряда расширяются до 48, при этом некоторые
разряды повторяются. Схема этого расширения показана ниже (номера соответствуют
номерам бит исходного 32-разрядного кода).
32 1 2 3 4 5
456789
8 9 10 11 12 13
12 13 14 15 16 17
16 17 18 19 20 21
20 21 22 23 24 25
24 25 26 27 28 29
28 29 30 31 32 1
Для полученного 48-разрядного кода и
ключа выполняется операция
исключающее ИЛИ (XOR). Результирующий
48-разрядный код преобразуется в 32разрядный с помощью S-матриц. На выходе
S-матриц осуществляется перестановка
согласно схеме показанной справа (числа
представляют собой порядковые номера
бит).
Рис. 9. Алгоритм работы функции f
16 7 20 21
29 12 28 17
1 15 23 26
5 18 31 10
2 8 24 14
32 27 3 9
19 13 30 6
22 11 4 25
Схема перестановки

42.

Дополнительные материалы для изучения
Алгоритм DES
Преобразование начинается с перестановки бит (IP - Initial Permutation) в 64разрядном блоке исходных данных. 58-ой бит становится первым, 50-ый - вторым и т.д.
Схема перестановки битов показана ниже.
58
60
62
64
57
59
61
63
50
52
54
56
49
51
53
55
42
44
46
48
41
43
45
47
34
36
38
40
33
35
37
39
26
28
30
32
25
27
29
31
18
20
22
24
17
19
21
23
10 2
12 4
14 6
16 8
91
11 3
13 5
15 7
Полученный блок делится на две 32-разрядные части L0 и R0. Далее 16 раз
повторяются следующие 4 процедуры:
1) Преобразование ключа с учетом номера итерации i (перестановки разрядов с удалением
8 бит, в результате получается 48-разрядный ключ).
2) Пусть A=Li, а J - преобразованный ключ. С помощью функции f(A,J) генерируется 32разрядный выходной код.
3) Выполняется операция XOR для Ri f(A,J), результат обозначается Ri+1.
4) Выполняется операция присвоения Li+1=Ri.

43.

Дополнительные материалы для изучения
Алгоритм DES
Структурная схема реализации алгоритма DEA показана на рис. 10.
Инверсная перестановка разрядов
предполагает следующее размещение 64 бит
зашифрованных данных (первым битом
становится 40-ой, вторым 8-ой и т.д.).
40
39
38
37
36
35
34
33
8
7
6
5
4
3
2
1
48
47
46
45
44
43
42
41
16 56 24 64 32
15 55 23 63 31
14 54 22 62 30
13 53 21 61 29
12 52 20 60 28
11 51 19 59 27
10 50 18 58 26
9 49 17 57 25
S-матрицы представляют собой таблицы
содержащие 4-ряда и 16 столбцов. Матрица
S(1) представлена ниже (эта матрица, также
как и те, что приведены в ссылке 2, являются
рекомендуемыми).
No. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7
1 0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8
2 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0
3 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13
Рис. 10. Структурная схема реализации
алгоритма DEA

44.

Дополнительные материалы для изучения
Алгоритм DES
Исходный 48-разрядный код делится на 8 групп по 6 разрядов. Первый и последний
разряд в группе используется в качестве адреса строки, а средние 4 разряда - в качестве
адреса столбца. В результате каждые 6 бит кода преобразуются в 4 бита, а весь 48разрядный код в 32-разрядный (для этого нужно 8 S-матриц). Существуют разработки,
позволяющие выполнять шифрование в рамках стандарта DES аппаратным образом, что
обеспечивает довольно высокое быстродействие.
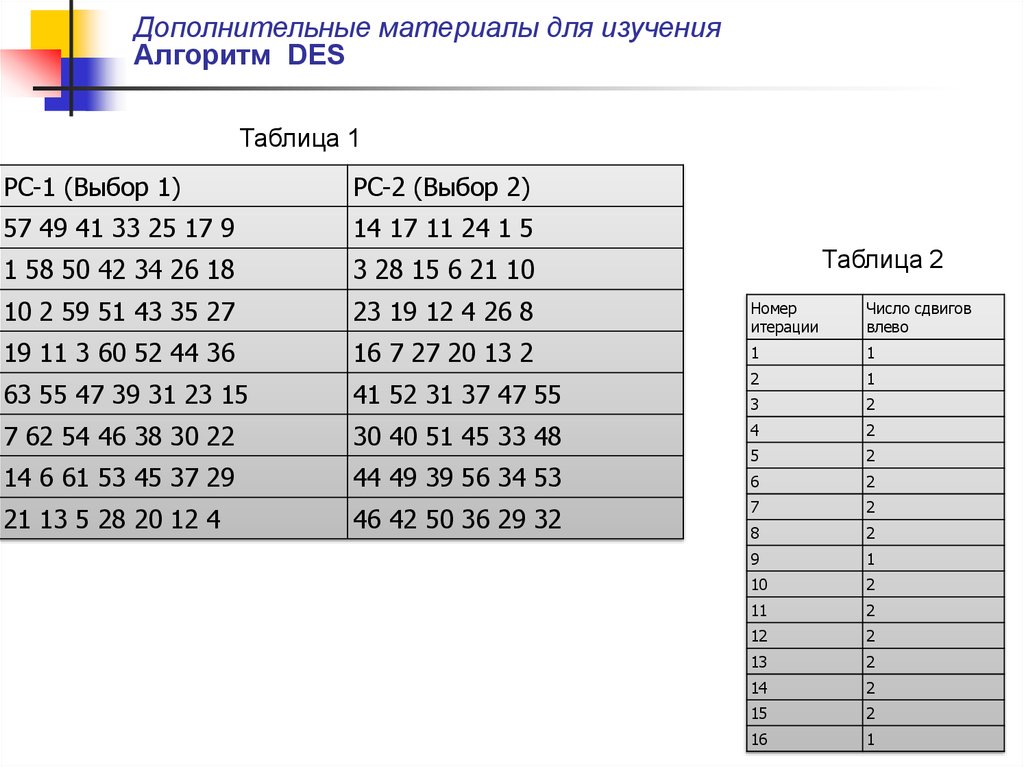
Преобразования ключей Kn (n=1,…,16; Kn = KS(n,key), где n - номер итерации)
осуществляются согласно алгоритму, показанному на рис. 11.
Для описания алгоритма вычисления ключей Kn
(функция KS) достаточно определить структуру
“Выбора 1” и “Выбора 2”, а также задать схему
сдвигов влево (табл. 2). “Выбора 1” и “Выбора 2”
представляют собой перестановки битов ключа (PC-1
и PC-2; табл. 1). При необходимости биты 8, 16,…, 64
могут использоваться для контроля четности.
Для вычисления очередного значения ключа таблица
делится на две части С0 и D0. В С0 войдут биты 57,
49, 41,…, 44 и 36, а в D0 - 63, 55, 47,…, 12 и 4. Так
как схема сдвигов задана (табл. 2) C1,D1; Cn, Dn и
так далее могут быть легко получены из C0 и D0.
Так, например, C3 и D3 получаются из C2 и D2
циклическим сдвигом влево на 2 разряда.
Рис. 11. Алгоритм вычисления
последовательности ключей Kn

45.

Дополнительные материалы для изучения
Алгоритм DES
Таблица 1
PC-1 (Выбор 1)
PC-2 (Выбор 2)
57 49 41 33 25 17 9
14 17 11 24 1 5
1 58 50 42 34 26 18
3 28 15 6 21 10
10 2 59 51 43 35 27
23 19 12 4 26 8
Номер
итерации
Число сдвигов
влево
19 11 3 60 52 44 36
16 7 27 20 13 2
1
1
2
1
3
2
Таблица 2
63 55 47 39 31 23 15
41 52 31 37 47 55
7 62 54 46 38 30 22
30 40 51 45 33 48
4
2
14 6 61 53 45 37 29
44 49 39 56 34 53
5
2
6
2
21 13 5 28 20 12 4
46 42 50 36 29 32
7
2
8
2
9
1
10
2
11
2
12
2
13
2
14
2
15
2
16
1

46.

Дополнительные материалы для изучения
Алгоритм шифрования RSA
Алгоритм RSA (Rivest, Shamir и Adleman, 1978 год) предполагает, что посланное
закодированное сообщение может быть прочитано адресатом и только им. В этом алгоритме
используется два ключа - открытый и секретный. Данный алгоритм привлекателен также в
случае, когда большое число субъектов (N) должно общаться по схеме все-со-всеми. В случае
симметричной схемы шифрования каждый из субъектов каким-то образом должен доставить
свои ключи всем остальным участникам обмена, при этом суммарное число используемых
ключей будет достаточно велико при большом значении N. Применение асимметричного
алгоритма требует лишь рассылки открытых ключей всеми участниками, суммарное число
ключей равно N.
Сообщение представляется в виде числа M. Шифрование осуществляется с
помощью общедоступной функции f(M), и только адресату известно, как выполнить
операцию f-1. Адресат выбирает два больших простых (prime) числа p и q, которые делает
секретными. Он объявляет n=pq и число d, c (d,p-1)=(d,q-1)=1 (один из возможных
способов выполнить это условие, выбрать d больше чем p/2 и q/2). Шифрование
производится по формуле:
f(M) ≡ Md mod n,
где M и f(M) оба ≤ n-1.
Как ранее было показано, это может быть вычислено за разумное время, даже
если M, d и n содержит весьма большое число знаков. Адресат вычисляет M на основе Md,
используя свое знание p и q. В соответствие со следствием 6, если
dc ≡ (p-1)1, тогда (Md)e ≡ p1.
Исходный текст числа M получается адресатом из зашифрованного F(M) путем
преобразования: M = (F(M))e (mod pq). Здесь как исходный текст, так и зашифрованный
рассматриваются как длинные двоичные числа.

47.

Дополнительные материалы для изучения
Алгоритм шифрования RSA
Аналогично (Md)e ≡ qM, если dc ≡ (q-1)1. e удовлетворяет этим двум условиям,
если cd ≡ (p-1) (q-1)1. Теорема 1 гласит, что мы можем позволить e=x, когда x является
решением уравнения dx + (p-1)(q-1)y = 1.
Так как (Md)e - M делимо на p и q, оно делимо и на pq, следовательно, мы можем
определить M, зная Md, вычислив его значение в степени e и определив остаток от деления
на pq. Для соблюдения секретности важно, чтобы, зная n, было нельзя вычислить p и q.
Если n содержит 100 цифр, подбор шифра связан с перебором ~1050 комбинаций. Данная
проблема изучается уже около 100 лет. RSA-алгоритм запатентован (20 сентября 1983,
действовал до 2000 года).
Теоретически можно предположить, что возможно выполнение операции f-1, не
вычисляя p и q. Но в любом случае задача эта не проста и разработчики считают ее трудно
факторизуемой.
Предположим, что мы имеем зашифрованный текст f(M) и исходный текст M, и мы
хотим найти значения p и q. Нетрудно показать, что таких исходных данных для решения
задачи недостаточно - надо знать все возможные значения Mi.

48.

Дополнительные материалы для изучения
Алгоритм шифрования RSA
Проясним использование алгоритма RSA на конкретном примере. Выбираем два
простые числа p=7; q=17 (на практике эти числа во много раз длиннее). В этом случае n =
p*q будет равно 119. Теперь необходимо выбрать e, выбираем e=5. Следующий шаг связан
с формированием числа d так, чтобы d*e=1 mod [(p-1)(q-1)]. d=77 (использован
расширенный алгоритм Эвклида). d - секретный ключ, а e и n характеризуют открытый ключ.
Пусть текст, который нам нужно зашифровать представляется M=19. С = Memod n.
Получаем зашифрованный текст C=66. Этот “текст” может быть послан соответствующему
адресату. Получатель дешифрует полученное сообщение, используя М= Cdmod n и C=66. В
результате получается M=19.
На практике общедоступные ключи могут помещаться в специальную базу данных.
При необходимости послать партнеру зашифрованное сообщение можно сделать сначала
запрос его открытого ключа. Получив его, можно запустить программу шифрации, а
результат ее работы послать адресату. На использовании общедоступных ключей базируется
и так называемая электронная подпись, которая позволяет однозначно идентифицировать
отправителя. Сходные средства могут применяться для предотвращения внесения каких-либо
корректив в сообщение на пути от отправителя к получателю. Быстродействующие
аппаратные 512-битовые модули могут обеспечить скорость шифрования на уровне 64 кбит в
сек. Готовятся ИС, способные выполнять такие операции со скоростью 1 Мбайт/сек.
Разумный выбор параметра e позволяет заметно ускорить реализацию алгоритма.

49.

Дополнительные материалы для изучения
Алгоритм шифрования AES
Стандарт AES (Advanced Encryption Standard) является стандартом шифрования
США, принятым в 2000-ом году.
Он специфицирует алгоритм Rijndael http://www.nist.gov/CryptoToolkit
(смотри также http://csrc.nist.gov/ publications/fips/fips197/fips-197.pdf).
Этот алгоритм представляет собой симметричный блочный шифр, который работает
с блоками данных длиной 128 бит и использует ключи длиной 128, 192 и 256 бит (версии
AES-28; AES-192 и AES-256). Сам алгоритм может работать и с другими длинами блоков
данных и ключей, но эта возможность в стандарт не вошла. При использовании 128-битного
ключа для взлома шифрования по заявлению правительства США потребуется 149
триллионов лет.
Биты данных нумеруются с нуля, начиная со старших. В AES основным является
полиномиальное представлением кодов. Так байт {01100011} следует представлять как:
x6 +x5 + x + 1.
Алгоритм AES производит операции над двумерными массивами байт, называемыми
структурами (state). Структура состоит из 4 рядов по Nb байт. Nb равно длине блока,
деленной на 32 (в данном стандарте Nb=4). Это позволяет обозначать структуру как sr,c или
s[r,c], где 0≤r<4 и 0≤с<4.
Входной код (in), который является последовательностью 16 байт можно
представить как:
s[r,c] =in[r +4c].

50.

Дополнительные материалы для изучения
Алгоритм шифрования AES
При реализации алгоритма AES используются операции сложения байт (по модулю
2 = XOR) и умножения. В алгоритме AES при умножении байтов используется неприводимый
многочлен:
m(x) = x8 + x4 + x3 + x + 1
[1]
Вычисление произведения М байтов {b1} на {b2} здесь выполняется согласно
следующему алгоритму:
M=[{b1}●{b2}] mod m(x).
[2]
В этом случае обратная величина байта равна:
полином:
образом:
{b}-1 ={b} mod m(x)
[3]
для умножения полубайтов (коды длиной 4 бита) используется неприводимый
m2(x) = x4 + 1
Вычисление произведения М полубайтов {a} на {b} здесь выполняется следующим
M=[{a}●{b}] mod m2(x).
[2a]
M представляет собой полубайт d. Операцию умножения полубайтов {a} на {b}
можно записать в матричном виде:
[4].

51.

Дополнительные материалы для изучения
Алгоритм шифрования AES
Как было сказано выше длины ключей Nk (длина, измеренная в 32 битных словах)
могут принимать значения 4, 6 или 8 (для AES-128, -192 и -256, соответственно). Число
итераций Nr (round), реализуемых в алгоритме AES, составляет соответственно 10, 12 и 14.
Шифрование
При запуске алгоритма шифрования входной блок данных копируется в массив
state. После первоначального добавления к state ключа массив state преобразуется с
помощью функции циклической обработки Nr раз (последний цикл несколько отличается от
предыдущих, см. рис. 19.3). Результат преобразования заносится в выходной массив.
Описание алгоритма в С-подобном
представлении отображено на рис. 12.
Преобразования SubByte(), ShiftRows(),
MixColumns() и AddRoundKey()
осуществляют обработку массива state.
Массив w[i] описан ниже.
Рис. 12. Псевдокод, реализующий
процедуру шифрования
Cipher(byte in[4*Nb], byte out[4*Nb], word
w[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in
AddRoundKey(state, w[0, Nb-1])
for round = 1 step 1 to Nr–1
SubBytes(state)
ShiftRows(state)
MixColumns(state)
AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])
end for
SubBytes(state)
ShiftRows(state)
AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])
out = state
end

52.

Дополнительные материалы для изучения
Алгоритм шифрования AES
Преобразование SubByte()
Преобразование SubByte() является нелинейной подстановкой байтов, которое
работает независимо для каждого байта State и использует таблицу подстановок S. Эта
замена включает в себя две операции:
1. Каждый байт заменяется на обратный мультипликативный (см. формулу 3). Байт {00}
преобразуется сам в себя.
2. Для каждого байта осуществляется аффинное преобразование в поле GF(2), задаваемое
формулой
[1.1]
Преобразование ShiftRows()
В преобразованиях ShiftRows() байты в последних трех рядах State циклически
сдвигаются на разное число байт. Первый ряд (r=0) не сдвигается. Преобразование
ShiftRows() осуществляется следующим образом:
для 0<r<4 и 0≤c<Nb
[1.3]
где величина сдвига shift(r,Nb) зависит от номера ряда r следующим образом:
shift(1,4)=1; shift(2,4)=2; shift(3,4)=3.

53.

Дополнительные материалы для изучения
Алгоритм шифрования AES
Преобразование MixColumns()
Преобразование MixColumns() обрабатывает State колонка за колонкой, каждая
из колонок представляет собой 4-битный код. Колонки рассматриваются как полиномы над
полем GF(28). Колонка умножается на фиксированный полином {a}={03}x3+{01}x2+{01}x+
{02} по модулю x4+1 (см. формулу 2а).
Преобразование AddRoundKey()
В преобразовании AddRoundKey() к State добавляется ключ итерации (Round Key;
побитовая операция XOR). Операция производится для каждого байта State.
Процедура расширения ключа
Ключи итерации вычисляются на основе ключа шифрования с помощью процедуры
преобразования ключа (Key expansion). Эта процедура формирует Nb(Nr+1) слов. Алгоритм
требует Nb слов и каждая из Nr итераций требует Nb слов. В результате получается
линейный массив 4-байтовых слов, который обозначается [wi], где i лежит в пределах 0?i
(см. рис. 13).
Функция SubWord() работает с входными байтами, преобразуя их с помощью Sтаблиц. Операция выполняется для каждого из 4 входных байт.
Функция RotWord() использует в качестве входного слова [a0,a1,a2,a3] и
возвращает слово [a1,a2,a3,a0].

54.

Дополнительные материалы для изучения
Алгоритм шифрования AES
KeyExpansion(byte key[4*Nk], word w[Nb*(Nr+1)], Nk)
begin
word temp
i=0
while (i < Nk)
w[i] = word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3])
i = i+1
end while
i = Nk
while (i < Nb * (Nr+1)]
temp = w[i-1]
if (i mod Nk = 0)
temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]
else if (Nk > 6 and i mod Nk = 4)
temp = SubWord(temp)
end if
w[i] = w[i-Nk] xor temp
i=i+1
end while
end
end
Рис. 13. Псевдокод реализации процедуры преобразования ключа

55.

Дополнительные материалы для изучения
Алгоритм шифрования AES
Расшифровка
Все процедуры, описанные в предыдущем разделе, являются обратимыми. Целью
дешифровки является обработка зашифрованного массива данных с целью получения
исходного блока данных. Процедуры дешифровки включают в себя функции
InvShiftRows(), InvSubBytes(), InvMixColumns() и AddRoundKey(). Псевдокод для
процедуры дешифровки представлен на рис. 14.
Рис. 14. Псевдокод процедуры дешифровки
InvCipher(byte in[4*Nb], byte out[4*Nb], word
w[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in
AddRoundKey(state,
w[Nr*Nb, (Nr+1)*Nb-1])
for round = Nr-1 step -1
downto 1
InvShiftRows(state)
InvSubBytes(state)
AddRoundKey(state,
w[round*Nb,
(round+1)*Nb-1])
InvMixColumns(state)
end for
InvShiftRows(state)
InvSubBytes(state)
AddRoundKey(state, w[0, Nb-1])
out = state
end

56.

Дополнительные материалы для изучения
Алгоритм шифрования AES
Преобразование InvShiftRows()
Процедура InvShiftRows() является обратной по отношению ShiftRows(). Байты
в последних трех рядах State циклически сдвигаются на разное число байт. Первый ряд (r=0)
не сдвигается.
Преобразование InvSubBytes()
Преобразование InvSubBytes() является обратной подстановкой байт, в которой
S-таблица последовательно применяется для каждого из байтов State. Это достигается за
счет обратного аффинного преобразования.
Преобразование InvMixColumns()
Процедура InvMixColumns() является обратной по отношению MixColumns() (см.
раздел 1.3). Колонки рассматриваются как полиномы над полем GF(28).
Обратное преобразование AddRoundKey()
Преобразование AddRoundKey(), описанное в разделе 1.4 является обратимым, так
как содержит только операции XOR.

57.

Дополнительные материалы для изучения
Алгоритм шифрования AES
Эквивалентный код дешифровки
В алгоритме дешифровки (рис. 14), последовательность преобразований отличается от
порядка операций шифрования, а форма ключей расширения для шифрования и
дешифрования остается неизменной (рис. 15). Однако ряд свойств алгоритма AES допускают
формирование эквивалентного кода дешифрования, где последовательность операций
преобразования остается той же самой (с заменой преобразований на обратные).
В последнее время появилась новая
версия AES-NI (New Instructions) [2], которая
позволяет оптимизировать работу алгоритма
(понизить загрузку процессора на 50%). Эта
версия может использоваться и совместно с
SSL. Компания Intel разработала микросхему,
реализующую этот алгоритм (серия X5600).
Количество клиентов при работе с версией
AES-NI может быть увеличено на 13%
EqInvCipher(byte in[4*Nb], byte out[4*Nb], word dw[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in
AddRoundKey(state, dw[Nr*Nb, (Nr+1)*Nb-1])
for round = Nr-1 step -1 downto 1
InvSubBytes(state)
InvShiftRows(state)
InvMixColumns(state)
AddRoundKey(state, dw[round*Nb, (round+1)*Nb-1])
end for
InvSubBytes(state)
InvShiftRows(state)
AddRoundKey(state, dw[0, Nb-1])
out = state
end
Для эквивалентной программы дешифровки в конец программы
расширения ключа добавляется следующий псевдокод:
С.Г. Баричев, В.В. Гончаров, Р.Е. Серов, Основы
современной криптографии, 2-е издание,
Москва, "Горячая линия - Телеком", 2002
for i = 0 step 1 to (Nr+1)*Nb-1
dw[i] = w[i]
end for
for round = 1 step 1 to Nr-1
InvMixColumns(dw[round*Nb, (round+1)*Nb-1])
Рис. 15. Псевдокод для эквивалентного
обратного преобразования