Similar presentations:
Применение производной к исследованию функций
1.
Тема «Применение производной к исследованию функцийy
x
2.
Производные простых функций(х – независимая переменная)
Производные сложных функций
(u=u(х) – любая дифференцируемая функция)
2
(C ) 0
( x n ) nx n 1
(C ) 0
(u n ) nu n 1 u
3
(a x ) a x ln a
(a u ) a u ln a u
4
(e x ) e x
(eu ) eu u
1
5
6
(log a x)
1
x ln a
1
(ln x) , x 0
x
u
(log a u )
u ln a
u
(ln u ) , u 0
u
7
(sin x) cos x
(sin u) cos u u
8
(cos x) sin x
(cos u ) sin u u
9
(tgx)
10
(ctgx)
1
cos 2 x
1
sin 2 x
u
cos 2 u
u
(ctgu) 2
sin u
(tgu)
3.
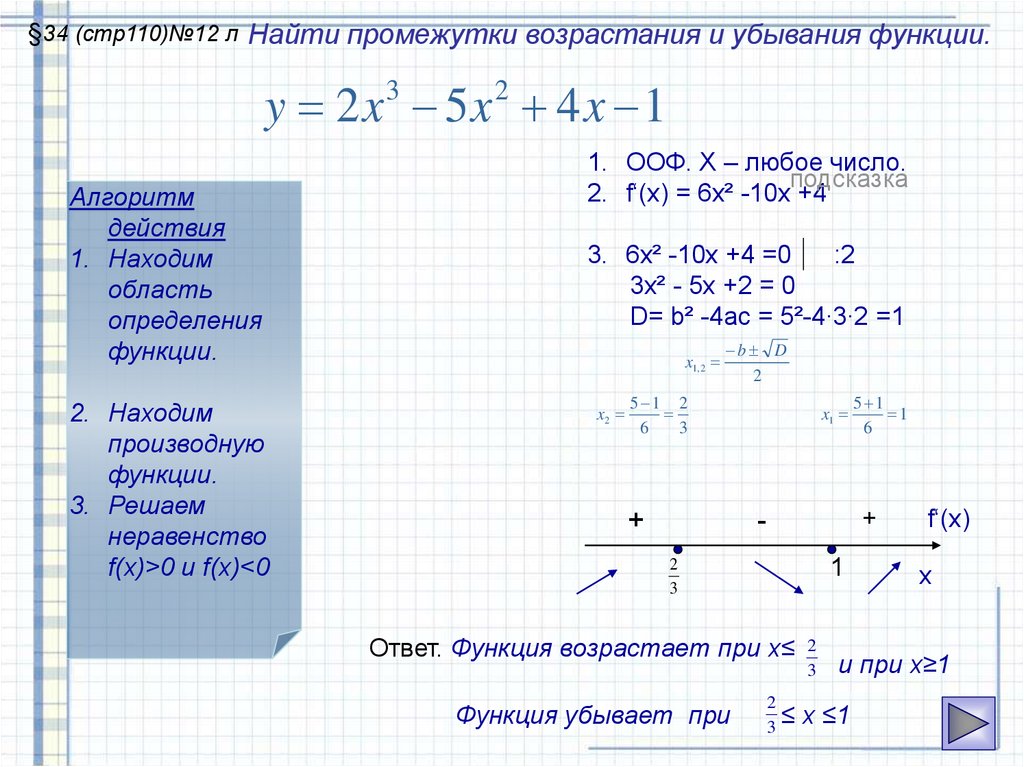
§34 (стр110)№12 л Найти промежутки возрастания и убывания функции.y 2x 5x 4x 1
3
Алгоритм
действия
1. Находим
область
определения
функции.
2. Находим
производную
функции.
3. Решаем
неравенство
f(x)>0 и f(x)<0
2
1. ООФ. Х – любое число.
подсказка
2. f‘(x) = 6x² -10x +4
3. 6x² -10x +4 =0
:2
3x² - 5x +2 = 0
D= b² -4ac = 5²-4∙3∙2 =1
x1, 2
x2
b D
2
5 1 2
6
3
+
x1
+
1
2
3
Ответ. Функция возрастает при х≤
Функция убывает при
5 1
1
6
2
≤
3
2
3
f‘(x)
x
и при х≥1
х ≤1
4.
ТемаНайти точки экстремума функции
1.
2.
х≠0
О.О.Ф.
4 x
y
x 16
х≠0
(делить на 0 нельзя)
Для нахождения производной представим условие в другой форме записи
4 1
1 1
y 4 2 2
x 16
x 16
3. Если
у‘=0
1 1
y 4 x
x 16
х≠0
x0 - точка экстремума дифференцируемой функции f(x), то f‘(x) =0
4 1
2 0
x 16
4
1
x 2 16
x 8
4. Точки минимума и точки максимума называются точками экстремума.
+ max
min +
х
0
8
-8
х≠0
Ответ .
Х=-8
Х= 8
точка максимума
точка минимума
5.
Тема «Алгоритм исследования свойств функции:
1. Найти область определения функции
2. Найти производную функции.
3. Найти критические точки функции.
4. Найти промежутки возрастания и убывания функции.
5. Найти точки экстремума и значения функции в этих точках.
6. Результаты исследования записываем в таблицу.
7. Находим значение функции в дополнительных точках
(если потребуется)
у
8. Строим график функции используя данные в таблице.
x
6.
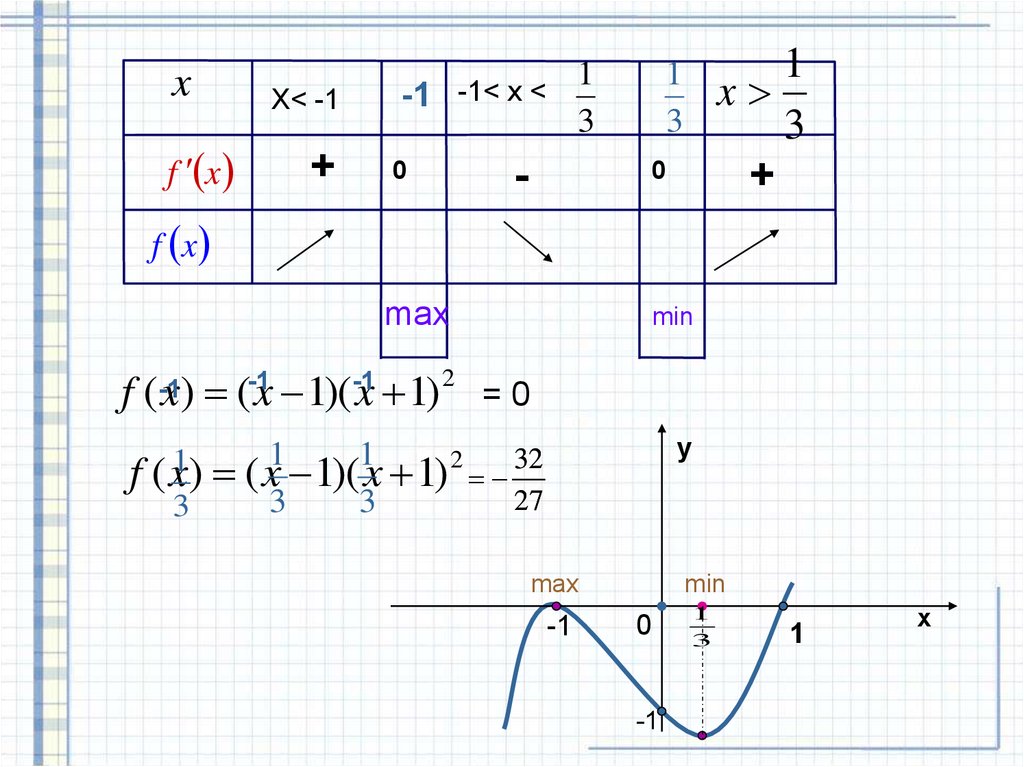
Исследовать функцию и построить ее графикf ( x) ( x 1)( x 1)
2
Алгоритм
1) D y R
2).
f ( x) ( x 1)( x 1) 2 ( x 1)( x 2 2 x 1)
x3 x 2 x 1
f ( x) 3x 2 2 x 1
3. f‘(x) = 0
3x 2 2 x 1 0
x1 1
4.
1
x2
3
+ max - min
1
1
3
+
x
7.
x1
-1 -1< x <
3
X< -1
f x
+
-
0
1
x
3
1
3
+
0
f x
max
min
f ( x) ( x 1)( x 1) = 0
-1
-1
2
y
1
1
1
( x) ( x 1)( x 1) 2 32
27
3
3
3
max
min
-1
1
3
0
f
-1
-1
1
x
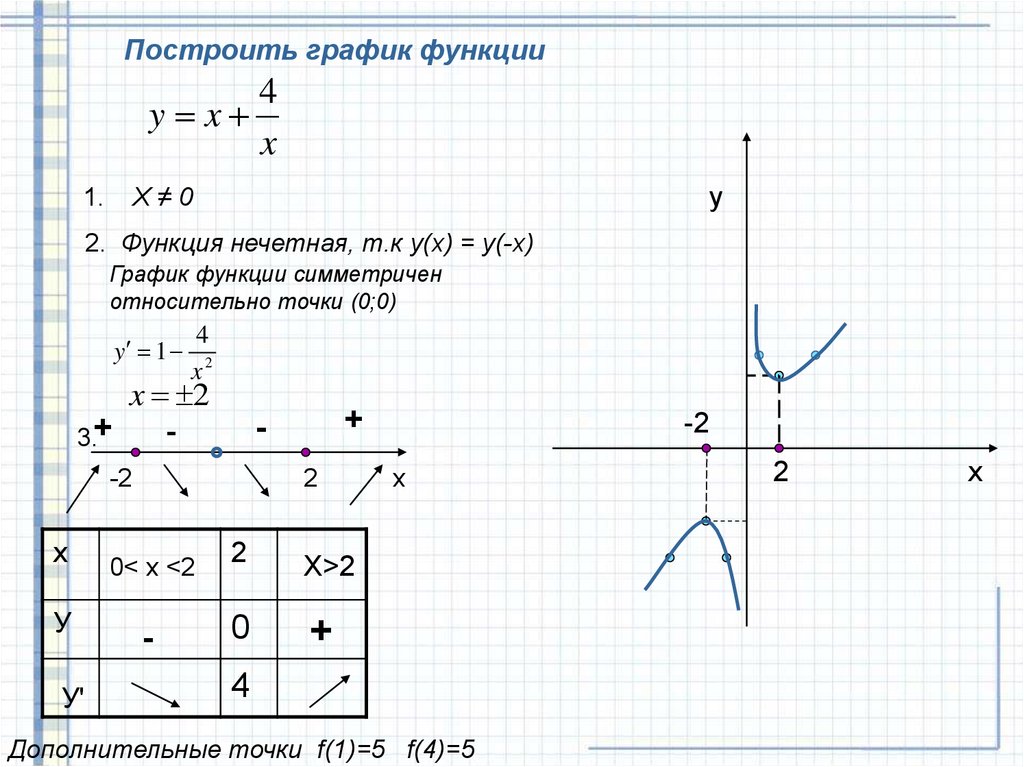
8.
Построить график функции4
y x
x
X≠0
1.
y
2. Функция нечетная, т.к у(х) = у(-х)
График функции симметричен
относительно точки (0;0)
y 1
4
x2
x 2
3.+
-2
х
У
У'
+
-
-
2
0< x <2
-
2
X>2
0
+
-2
х
4
Дополнительные точки f(1)=5 f(4)=5
2
x
9.
АлгоритмДля нахождения наибольшего и наименьшего значений
функции f(x) на отрезке [a; b] нужно:
1. найти значения функции на концах отрезка, т.е.
числа f(a) и f(b);
2.найти её значения в тех критических точках,
которые принадлежат интервалу (a; b);
3/из найденных значений выбрать наибольшее и
наименьшее.
10. Найти наибольшее (или наименьшее) значение функции
Найти наибольшее (или наименьшее) значение16
функции
f x x 2 2 на интервале x 0
x
1) f x x 2 16 x 2 2 x 32 x 3
2 x 4 16
2 x 2 4 x 2 4
3
3
x
x
32 2 x 4 32
2x 3
3
x
x
2 x 2 x 2 x 2 4
x3
2) f x 0 при x1 2, x2 2 0;
3) f x не существует при x 0 0;
16
16
4) f 2 2 2 4 8
2
4
2
Ответ : 8 наименьшее значение.
Алгоритм
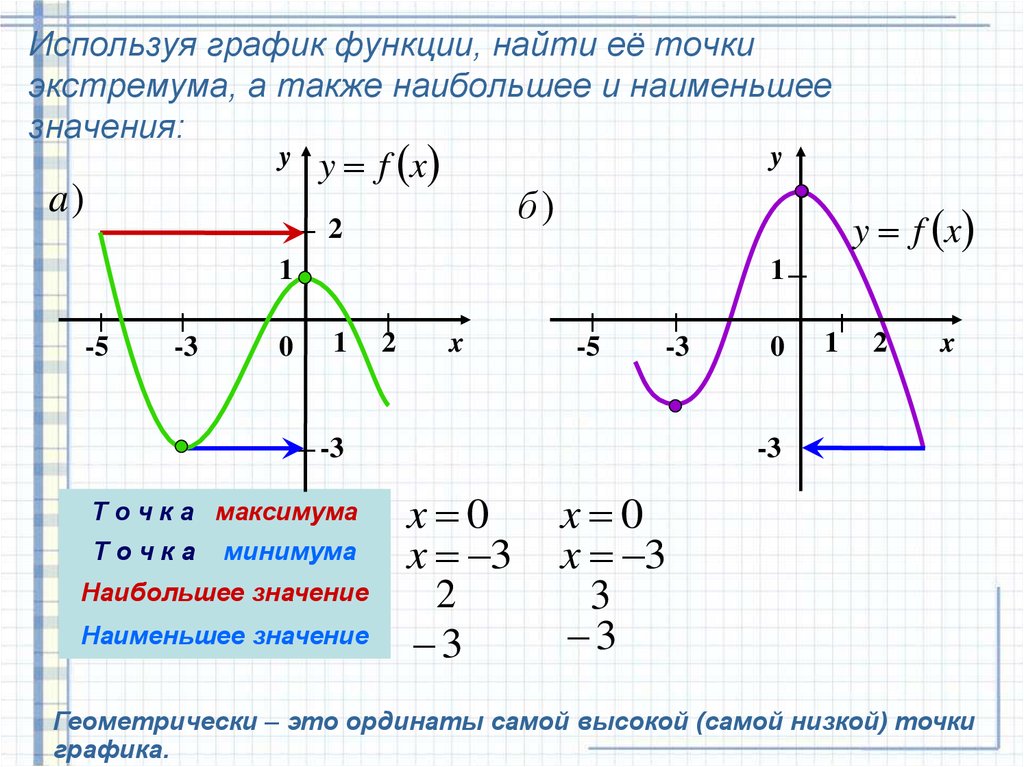
11. Используя график функции, найти её точки экстремума, а также наибольшее и наименьшее значения:
ya)
y f x
y
б)
I
2
y f x
I
-5
I
-3
0
1
I
1
1
x
I
-5
I
минимума
Наибольшее значение
Наименьшее значение
I
-3
-3
Т о ч к а максимума
Точка
I
2
0
I
1
2
x
-3
x 0
x 3
2
3
x 0
x 3
3
3
Геометрически – это ординаты самой высокой (самой низкой) точки
графика.







 mathematics
mathematics








