Дискретные структуры. Теория множеств. Отношения

1. ТЕОРИЯ МНОЖЕСТВ ОТНОШЕНИЯ

ДИСКРЕТНЫЕ СТРУКТУРЫ
ТЕОРИЯ МНОЖЕСТВ
ОТНОШЕНИЯ
ЛЕКЦИЯ 3
Математический факультет. Кафедра математического
моделирования
1

2. Цель лекции – ознакомиться и овладеть понятиями «отношение», «алгебра отношений», изучить операции над отношениями для

Тема: Отношения
Цель лекции – ознакомиться и овладеть понятиями
«отношение», «алгебра отношений», изучить операции
над отношениями для применения в задачах
компьютерной инженерии
Содержание:
• Понятие n-местного отношения.
Совместимость отношений
• Операции над отношениями
• Реляционная алгебра
• Дополнительные операции над
отношениями
• Пример применения отношений
при составлении реляционной
базы данных
2

3.

Литература
• Горбатов В.А. Основы дискретной математики. М.: Высш. шк.,
1986. 9-12 с.
• Лавров И.А., Максимова Л.Л. Задачи по теории множеств,
математической логике и теории алгоритмов. М.: Наука. Главная
редакция физико-математической литературы, 1984. 8-12 с.
• Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная
математика для инженера. М.: Энергия, 1980. 12-21 с.
• Богомолов А.М., Сперанский Д.В. Аналитические методы в
задачах контроля и анализа дискретных устройств. Саратов: Изд-во
Саратовкого ун-та, 1986. 240с.
• Новиков Ф.А. Дискретная математика для программистов. С.-П.,
2001. С. 4-24.
• Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В.
Методичні вказівки до практичних занять з курсу “Дискретна
математика”. Харків, ХНУРЕ. 2001. 21-23 с.
3

4.

Термины
Базовые
понятия:
множество,
подмножество,
упорядоченная
пара,
вектор,
декартово
(прямое)
произведение
множеств
Ключевые слова:
отношение,
степень отношения,
совместимость отношений,
реляционная алгебра,
операции над отношениями:
объединение,
пересечение,
разность,
расширенное декартово
произведение,
выбор,
проекция,
соединение
4

5.

Определение отношения
Def: n-местным отношением на
множестве M называется подмножество
декартовой степени множества М:
n
Rn М
Элементы х1, х2, …, хn находятся в
отношении, если (х1, х2, …, хn) Rn
n – степень отношения (-арность)
2
R A – бинарное отношение;
3
R A – тернарное отношение;
n
R A – n-арное отношение
Совместимые отношения – отношения
одинаковых степеней
Множества
Декартово
произведение A B,
М1 М2 … Мn
Декартова
степень Мn
Отношение Rn М
5
n

6.

Операции над отношениями. 1
Для совместимых отношений α An, β Вn имеют место
следующие операции:
Название операции
Объединение отношений
Пересечение отношений
Разность отношений
Определение
{v | v или v }
{v | v и v }
\ {v | v и v }
6

7.

Операции над отношениями. 2
Название операции
Определение
Дополнение β отношения β
есть разность α\β,
β = α\β =(А В)\ β
если α=А В –
универсальное отношение
Расширенное декартово
{p (k , k ) | k , k }
произведение α β (α и β
могут быть
p – конкатенация кортежа kα с
несовместимыми)
кортежем kβ
7

8.

Пример 1
Для совместимых тернарных отношений , M3
={(a,b,c), (a,b,d), (b,c,e)}
={ (a,b,d), (b,d,e), (c,d,e)}
операции объединения, пересечения и разности
определяются как:
={(a,b,c), (a,b,d), (b,c,e), (b,d,e), (c,d,e)};
={ (a,b,d) };
\ ={(a,b,c), (b,c,e) }
8

9.

Пример 2
Даны множества: A={a,b}, B={a,c}
Составим их декартовы квадраты:
A2={ (a,a), (a,b), (b,a), (b,b) },
B2={ (a,a), (a,c), (c,a), (c,c) }
Отношения задаются следующим образом:
=A B={ (a,a), (a,c), (b,a), (b,c) }
={ (a,c), (c,a) } B2
Дополнение отношения есть :
\ ={ (a,a), (b,a), (b,c) }
9

10.

Пример 3
Даны отношения A2, A3
{ (a,b), (c,d), (a,e) },
={(a,b,c), (b,d,e)}
Расширенное декартово произведение
отношений и определяется как
= { (a,b,a,b,c), (a,b,b,d,e), (c,d,a,b,c),
(c,d,b,d,e), (a,e,a,b,c), (a,e,b,d,e) }
10

11.

Алгебра отношений. 1
Отношения в совокупности с операциями образуют
реляционную алгебру.
Алгебра отношений или модель (множество с
заданным отношением) широко применяются при
формализации реальных объектов, создании
информационного обеспечения – разработке
информационной базы данных
Основой построения реляционной базы данных
является двумерная таблица, каждый столбец
которой соответствует домену (или атрибуту,
являющемуся частью домена), строка – кортежу
значений атрибутов, находящихся в отношении R
11

12.

Алгебра отношений. 2
Носитель реляционной алгебры
представляет собой множество отношений
Сигнатура, кроме введенных операций,
включает специальные операции над
отношениями:
выбор,
проекция,
соединение
В соответствии с потребностями практики
вводятся и другие операции:
обмен позициями;
удвоение позиций;
свертка, композиция.
12

13.

Time Out
Преподаватель (П) и студент (С):
П: Знаешь?
С: Знаю!
П: Что знаешь?
С: Предмет знаю.
П: Какой предмет?
С: Который сдаю.
П: А какой сдаешь?
С: Ну, это Вы придираетесь.
Ваш, конечно!
13

14.

Пример специальных операций
над отношениями. Постановка задания. 1
Таблица определяет отношение реляционной модели данных:
D1 D2 D3
a1 b2 c2
a2 b1 c3
a3 b3 c4
a4 b4 c3
R5
a1 b3 c4
a2 b2 c2
a3 b4 c3
a4 b1 c2
D4
f3
f3
f3
f1
f2
f2
f4
f4
D5
g1
g2
g2
g1
g1
g2
g2
g1
g
14

15.

Пример специальных операций
над отношениями. Постановка задания. 2
Определить результаты выполнения следующих операций:
1 – выбор по домену D3 по значению атрибута c2 ;
2 – проекция по домену D5 ;
3 – проекция по доменам D2, D5 ;
4 – соединение по домену D1 по условию «равно» для
двух таблиц (первые четыре кортежа R5) и g (вторые
четыре кортежа R5).
15

16.

Пример специальных операций
над отношениями. Выбор. 1
1 – выбор по домену D3 по значению c2 :
D1 D2 D3
a1 b2 c2
a2 b1 c3
a3 b3 c4
a4 b4 c3
R5
a1 b3 c4
a2 b2 c2
a3 b4 c3
a4 b1 c2
D4
f3
f3
f3
f1
f2
f2
f4
f4
D5
g1
g2
g2
g1
g1
g2
g2
g1
g
16

17.

Пример специальных операций
над отношениями. Выбор. 2
Def: операция выбора представляет собой
процедуру построения «горизонтального»
подмножества отношения, т.е. подмножества
кортежей, обладающих заданным свойством
1 {(a1, b2 , c2 , f 3 , g1 ), (a2 , b2 , c2 , f 2 , g 2 ), (a4 , b1, c2 , f 4 , g1 )},
17

18.

Пример специальных операций
над отношениями. Проекция. 1
Def: операция проекции
определяет построение
«вертикального» подмножества
отношения или множества
кортежей, получаемого выбором
одних и исключением других
доменов:
2 – проекция по домену D5
D1 D2 D3
a1 b2 c2
a2 b1 c3
a3 b3 c4
a4 b4 c3
R5
a1 b3 c4
2={g1,g2}
3 – проекция по доменам D2, D5:
a2 b2 c2
a3 b4 c3
3 {(b2 , g1), (b1, g 2 ), (b3 , g 2 ), (b4 , g1),
(b3 , g1), (b2 , g 2 ), (b4 , g 2 ), (b1, g1)},
a4 b1 c2
18
D4
f3
f3
f3
f1
f2
f2
f4
f4
D5
g1
g2
g2
g1
g1
g2
g2
g1
g

19.

Пример специальных операций над
отношениями. Проекция. 2
Def: проекцией Pr(R2/A) бинарного отношения
R2 A B на множество А называется множество
элементов
Pr(R2/A)={ai | (ai,bi) R2}
Def: проекцией Pr(Rn/Ai1,Ai2,…,Aim) n-арного
отношения Rn Ai1 Ai2 … Ain на множества
Ai1,Ai2,…,Aim называется множество кортежей
ai1,ai2,…,aim, где aij Aij , каждый из которых является
частью n-арного отношения:
Pr(Rn/Ai1,Ai2,…,Aim)={(ai1,ai2,…,aim)| aij Aij , j=1,2,…,m}
19

20.

Пример специальных операций
над отношениями. Соединение. 1
4 – соединение по домену
D1 D2 D3
D1 по условию «равно» для
a1 b2 c2
двух таблиц (первые четыре
a2 b1 c3
кортежа R5) и g (вторые
a3 b3 c4
четыре кортежа R5):
4 {( a1, b2 , c2 , f 3 , g1, b3 , c4 , f 2 , g1 ),
a4 b4 c3
R5
(a2 , b1, c3 , f 3 , g 2 , b2 , c2 , f 2 , g 2 ),
a1 b3 c4
(a3 , b3 , c4 , f 3 , g 2 , b4 , c3 , f 4 , g 2 ),
a2 b2 c2
(a4 , b4 , c3 , f1, g1, b1, c2 , f 4 , g1 )}.
a3 b4 c3
a4 b1 c2
D4
f3
f3
f3
f1
f2
f2
f4
f4
D5
g1
g2
g2
g1
g1
g2
g2
g1
20
g

21.

Пример специальных операций над
отношениями. Соединение. 2
Def: операция соединения по двум
таблицам, имеющим общий домен,
позволяет построить одну таблицу,
каждая строка которой образуется
соединением двух строк исходных
таблиц. Из заданных таблиц
выбираются строки, содержащие
одно и то же значение из общего
домена; общему домену
сопоставляется один столбец
21

22. Выводы

Реляционная алгебра замкнута относительно
введенных операций
Операция проецирования на один домен
выводит из носителя, например, результат
действия операции проекции по домену D5
отношением не является
Проекция на два и более домена является
отношением степени два и более,
соответственно
Запрос в реляционной базе данных будет
выполнен тем быстрее, чем меньше операций
над отношениями он содержит
22

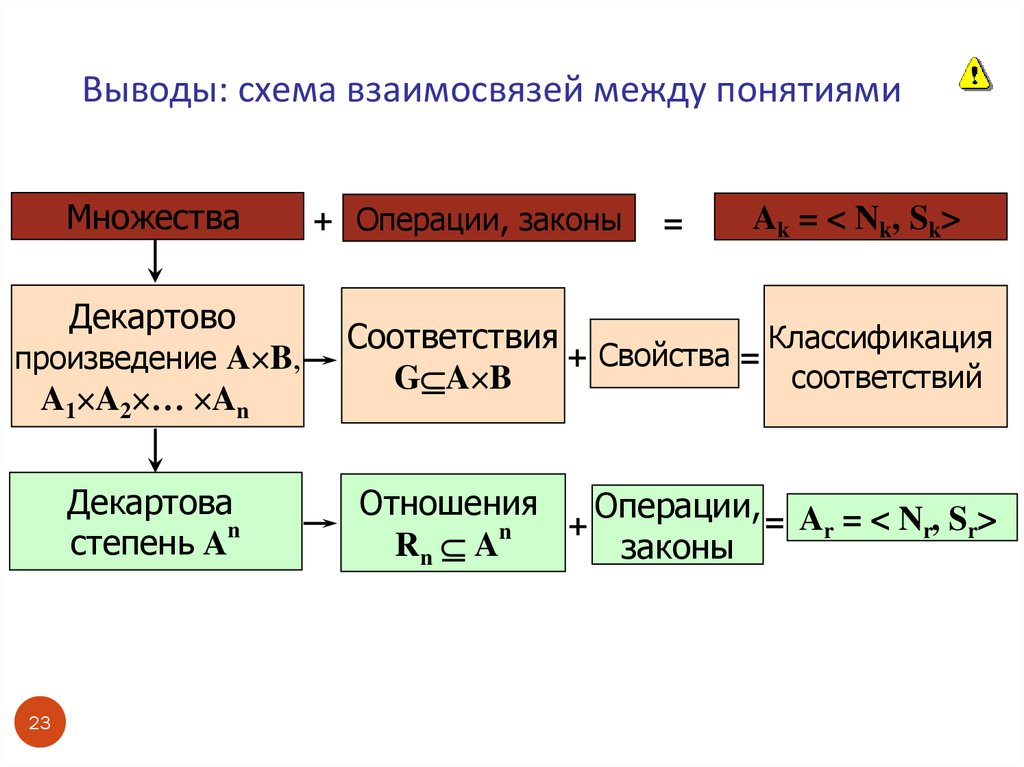
23. Выводы: схема взаимосвязей между понятиями

Множества
+ Операции, законы
=
Ak = < Nk, Sk>
Декартово
произведение A B,
A1 A2 … An
Классификация
Соответствия
+ Свойства =
соответствий
G A B
Декартова
степень An
Отношения
Операции, = A = < N , S >
+
r
r
r
Rn An
законы
23

24.

Тест-вопросы. 1
1. Отношением степени n называется:
а) произвольное подмножество
данного множества;
б) подмножество декартова
произведения двух множеств;
в) подмножество декартова
произведения любого конечного
количества множеств;
г) подмножество декартовой степени
множества;
д) результат объединения данных
множеств;
е) результат пересечения данных
множеств.
2. Отношения являются совместимыми:
а) всегда;
б) если они имеют разные степени;
в) если они имеют одинаковые степени;
г) если они бинарные.
3. Операция выбора представляет собой
построение:
а) «горизонтального» подмножества
отношения;
б) «вертикального» подмножества
отношения;
в) «диагонального» подмножества
отношения;
г) «бинарного» подмножества
отношения;
24

25.

Тест-вопросы. 2
4. Операция проекции представляет собой
построение:
а) «горизонтального»
б) «вертикального»
в) «диагонального»
подмножества отношения.
5. Операция проекции по двум доменам
представляет собой построение:
а) «горизонтального» подмножества
отношения;
б) «вертикального» подмножества
отношения;
в) «диагонального» подмножества
отношения;
г) бинарного подмножества отношения.
6. Операция проекции по одному
домену представляет собой
построение:
а) «горизонтального»
подмножества отношения;
б) «вертикального» подмножества
отношения;
в) «диагонального» подмножества
отношения;
г) бинарного подмножества
отношения;
д) некоторого отношения степени
n;
е) множества элементов, не
являющегося отношением.
25