Моделирование в среде TCAD

1.

Моделирование в среде TCAD
Семинар 3

2. Моделирование технологических процессов в Sentaurus Process Диффузия. Окисление.

3. Моделирование процесса диффузии

Диффузия – физический процесс,
обуславливающий миграцию атомов
легирующих примесей в кристаллической
решетке кремния.
Диффузия приобретает направленное движение
под влиянием либо градиента концентрации,
либо градиента температуры
(в микроэлектронном производстве градиенты
температуры в подложке – отрицательное
явление и не используется на практике)
3

4. Основное уравнение для процесса диффузии (Sentaurus Process)

J- поток диффундирующих частиц,
с – зарядовое состояние,
d – коэффициент диффузии,
A – концентрация примеси типа а,
n – концентрация электронов
4

5. Уравнение непрерывности для примеси типа a в зарядовом состоянии c

N ac
TR
CL
J ac Rac Rac
t
TR
ac
- вклад генерации – рекомбинации, связанный с
моделью переноса,
R
CL
ac
R
- вклад генерации – рекомбинации, связанный с
процессом кластеризации
5

6. Модели диффузии

• Модели переноса позволяют рассчитать поток частиц
примеси и являются основой моделирования диффузии
в программе Sentaurus Process.
• В дополнение к расчету потоков частиц могут быть
учтены возможные реакции взаимодействия частиц в
процессе диффузии в зависимости от выбранного типа
модели.
• Модели переноса обычно используются с одной или
несколькими моделями кластеризации или активации.
Реакции взаимодействия или модели кластеризации не
модифицируют поток частиц, а добавляют в уравнении
непрерывности слагаемые к
6

7. Модель диффузии ChargedReact

• Модель диффузии ChargedReact – наиболее
полная модель переноса в программе
Sentaurus Process.
• Модель включает неподвижную примесь в
замещающем состоянии и до двух
подвижных заряженных пар примесьдефект.
• Также в рассмотрение включены
подвижные заряженные точечные дефекты.
7

8. Реакции в модели диффузии ChargedReact

A – замещающие
атомы примеси
I – междоузлия
V - вакансии
8

9. Дифференциальные уравнения в модели ChargedReact

CA – концентрация
замещающих атомов
примеси
CI – концентрация
междоузлий
CV – концентрация
вакансий
CAX- концентрация
пар дефект-примесь
(I или V)
9

10. Модель ChargedReact : уравнение для заряженных пар

• Предполагается, что реакция образования пар дефектпримесь является равновесной:
где X это I или V, z –
заряд примеси A
- Скорость реакции
образования пар AX

11.

• Поток пар:
• Потокт дефектов:
• Скорости для всех комбинаций зарядовых
состояний:

12. Типы моделей

ChargedReact Diffusion Model
React Diffusion Model
ChargedPair Diffusion Model
Pair Diffusion Model
ChargedFermi Diffusion Model
Fermi Diffusion Model
Constant Diffusion Model
NeutralReact Diffusion Model

13. Пары дефект – примесь, участвующие в диффузии основных типов примеси

Вклад пар в диффузию можно учесть при определении эффективного
коэффициента диффузии по принципу суперпозиции, умножая каждую
составляющую на весовой коэффициент
Фосфор
Пара дефект
- примесь
Весовой
коэффициент
P +I -
P +I 0
P +I +
P+V=
1
1
1
1
Мышьяк
Пара дефект
- примесь
Весовой
коэффициент
As+I=
As+I-
As+I0
As+I+
As+V=
As+V-
As+V0
As+V+
0.2
0.2
0.2
0.2
0.8
0.8
0.8
0.8
Бор
Пара дефект
- примесь
Весовой
коэффициент
B-I-
B-I0
B-I+
B-I++
B-V-
B-V0
B-V+
B-V++
0.92
0.92
0.92
0.92
0.02
0.02
0.02
0.02
13

14. Кинетический метод Монте-Карло для расчета процесса диффузии (KMC)

15.

• Кинетический метод Монте-Карло
рассчитывает траектории
индивидуальных примесей и точечных
дефектов и взаимодействие между ними.
• Метод позволяет изучать процесс
диффузии на микроскопическом уровне.
• Результаты моделирования с помощью
КМС могут быть использованы для
калибровки моделей, основанных на
решении уравнений диффузии.

16. Преимущества метода Монте-Карло

Преимущества метода МонтеКарло
• Уменьшение термического бюджета в
современных технологических
маршрутах сокращает
продолжительность диффузионых
процессов, преобладают
термодинамически неравновесные
процессы и состояния.

17.

• При обычном подходе к моделированию число
решаемых уравнений быстро возрастает с
учетом всех возможных пар дефект – примесь,
переходов и состояний.
• С другой стороны, уменьшение размеров
приборов приводит к малому количеству
атомов примеси, формирующих структуру
прибора (десятки или сотни). Приближается
предел, когда такие малые дискретизованные
распределения уже не могут быть
аппроксимированы непрерывными функциями.

18. Повышение конкурентноспособности метода Монте-Карло

• С уменьшением размеров трудоемкость метода
Монте-Карло снижается, т.к. уменьшается
число атомов и дефектов, вовлеченных в
процесс.
• Большое количество различных конфигураций
дефект – примесь не усложняет метод, т.к.
требует только введения значений
вероятностей для дополнительных реакций.
• Трудоемкость обычного метода
моделирования систем уравнений возрастает
из-за неравновесных процессов

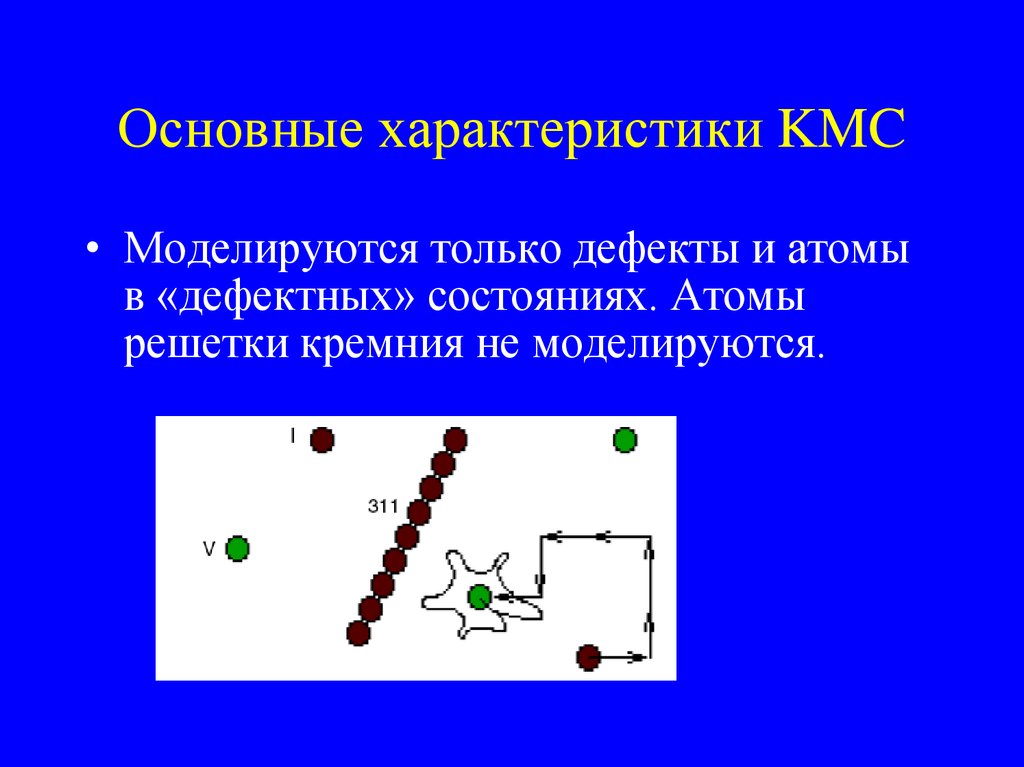
19. Основные характеристики KMC

• Моделируются только дефекты и атомы
в «дефектных» состояниях. Атомы
решетки кремния не моделируются.

20. Основные характеристики KMC

• Входные параметры – энергии миграции,
связи, эмиссии и др.
• По ним рассчитывается вероятность
(частота) того или иного события.
• Частицы могут также взаимодействовать
с протяженными дефектами или
двигаться вдоль них.

21. Основные характеристики KMC

• КМС (на базе программы DADOS)
может работать в 2-х режимах:
– Атомистическом (наиболее точный)
– Неатомистическом, с использованием
модуля KMC для отдельных операций,
прежде всего неравновесных процессов
(RTA и др.)

22. Атомистический режим

• Распределения всех величин рассчитываются
полностью на основе расчета траекторий
отдельных атомов
• Основные ограничения данного режима:
– Осаждение слоев возможно только без учета
примеси;
– Имплантация должна моделироваться только с
помощью Sentaurus MC
– Окисление не моделируется.

23.

• КМС использует ортогональную сетку и
разбиение моделируемой области на
прямоугольные поддомены.

24. Используемые материалы

Кремний (монокристаллический)
Аморфный кремний
Диоксид кремния
Поликристаллический кремний
Нитрид кремния
Газ (внешняя среда)

25. Типы частиц

26.

• Точечные дефекты могут взаимодействовать
с соседними частицами и перемещаться на
расстояние λ в ортогональных направлениях

27.

• Атомы акцепторной или донорной
примеси могут диффундировать в паре с
дефектом (вакансией или междоузлием)
• Пара дефект – примесь может
– диффундировать
– распадаться на атом примеси в
замещаюшем состоянии (заряженный,
неподвижный) и точечный дефект

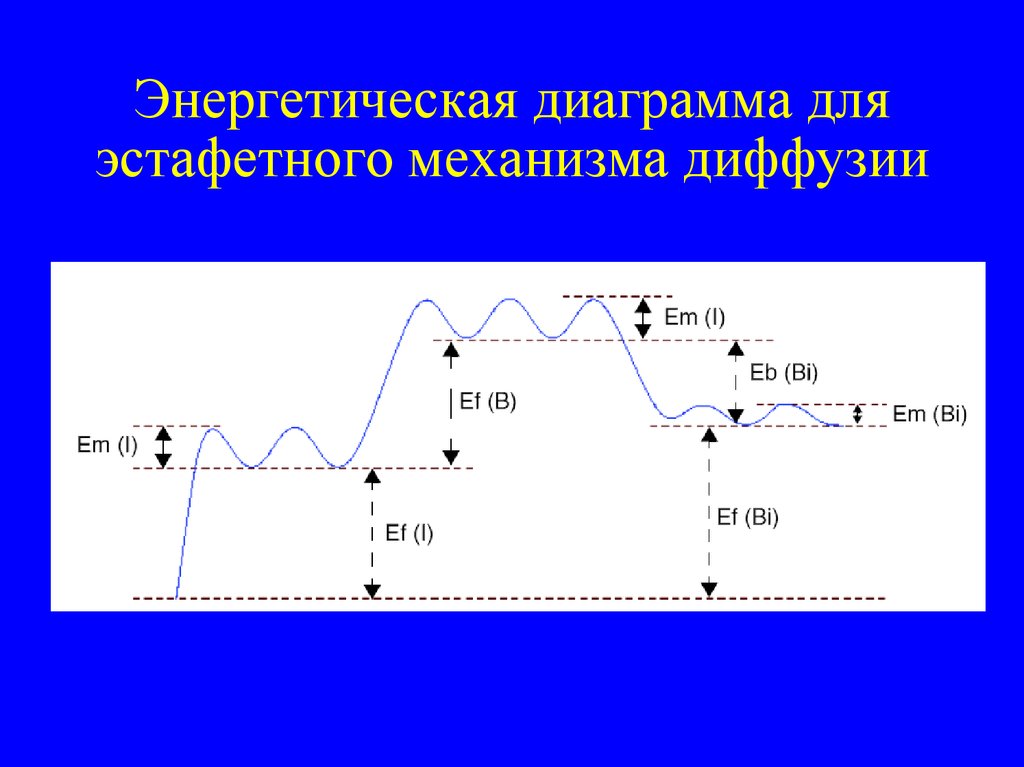
28. Энергетическая диаграмма для эстафетного механизма диффузии

29.

• Не все возможные сочетания
частиц участвуют в реакциях.
• Возможные реакции включают
физически обоснованные типы
взаимодействий.
• Рассматриваются только обратимые
реакции, реакции со стабильными
выходными продуктами.
Например, допустимые реакции для бора:

30. Области аккумуляции дефектов

Аморфные зоны

31. Протяженные дефекты

• {311} дефекты
• Кольца дислокаций
• Пустоты (вакансионные кластеры)

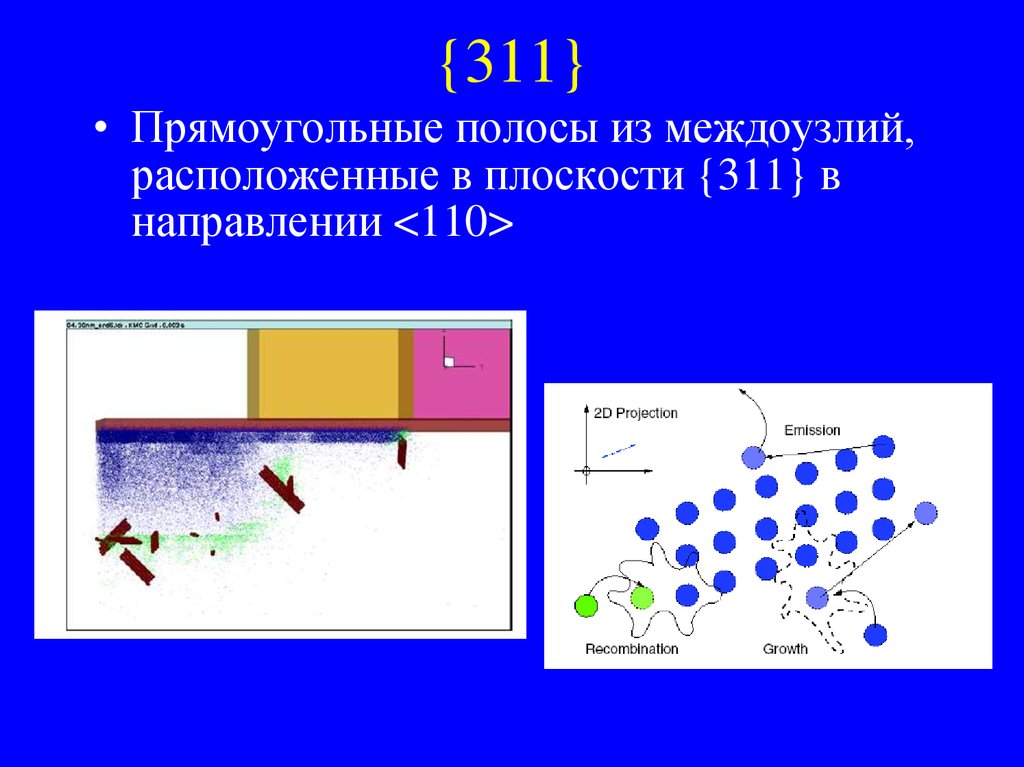
32. {311}

• Прямоугольные полосы из междоузлий,
расположенные в плоскости {311} в
направлении <110>

33. Кольца дислокаций

• Тонкие круги в плоскости {111}

34. Вакансионные кластеры (пустоты)

• Кластер из 654 вакансий
(моделирование)

35. Кластеризация примеси

• Кластеры мышьяк – вакансии
(синий-мышьяк, зеленыйвакансия)
→

36. Зарядовые состояния

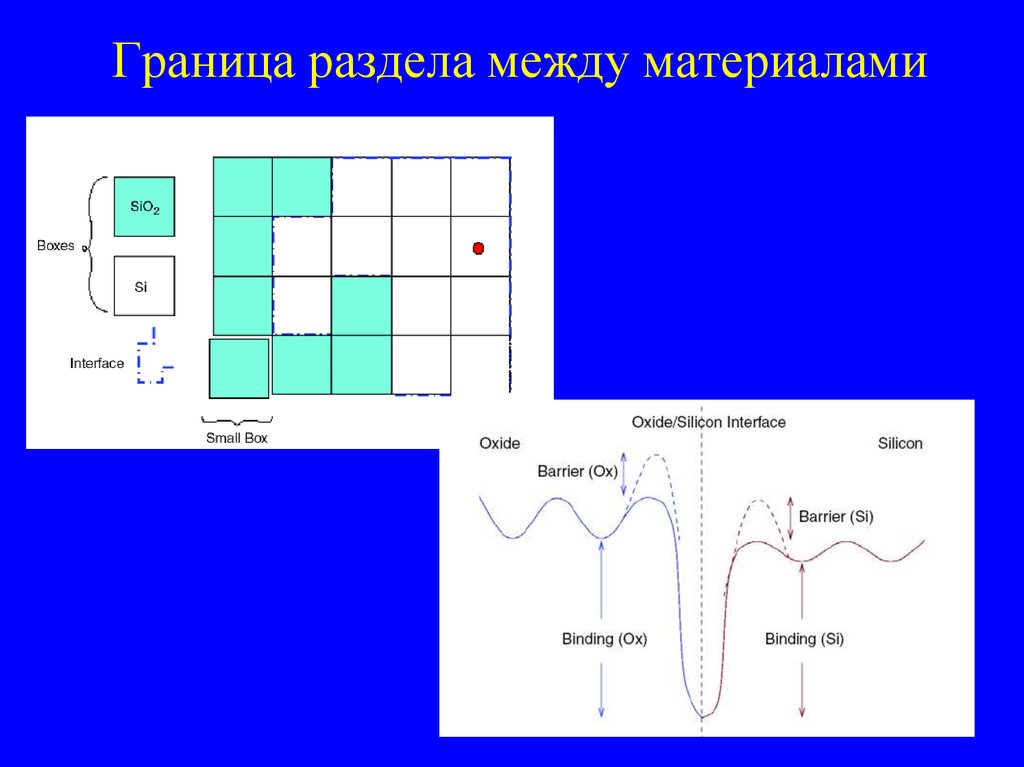
37. Граница раздела между материалами

38. Моделирование диффузии в процессе окисления

• На каждом шаге решается система уравнений для
расчета процесса окисления и механических
напряжений
• Перед запуском шага моделирования диффузии
методом КМС трансформируется сетка.
• Вновь выращенный окисел встраивается в тензорную
сетку, используемую в КМС
• Материал и свойства частиц изменяются там, где
необходимо
• Недостаток: несовершенство интерполяции при
переходе от непрерывной сетки к тензорной

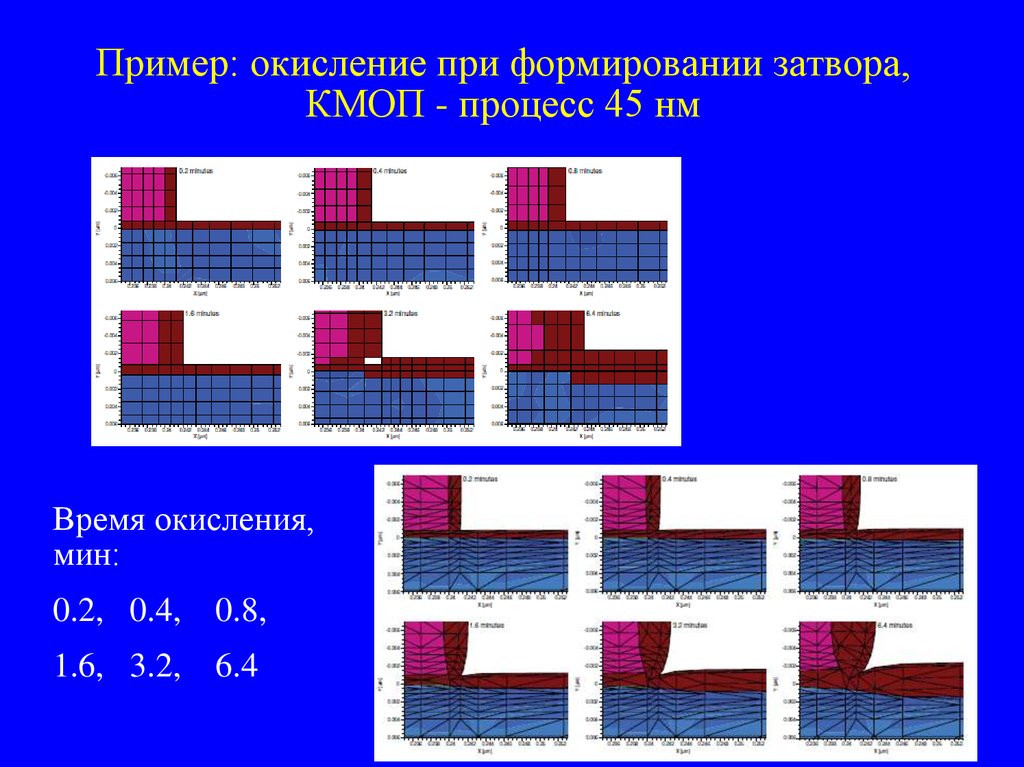
39. Пример: окисление при формировании затвора, КМОП - процесс 45 нм

Время окисления,
мин:
0.2, 0.4, 0.8,
1.6, 3.2,
6.4

40.

Моделирование методом Монте-Карло имплантации P(30
КэВ, 1е14) и отжига (800 С, 15 мин.)
1 эксперимент
Усреднение по 20-ти экспериментам

41.

Sentaurus Process
Kinetic Monte Carlo
• Неоднородная
тензорная сетка
• Механические
напряжения и SiGe
• Дополнительные
физические модели
МОП-транзистор:
моделирование с
помощью Sentaurus
Process KMC.
41

42.

• Полное описание см.
• Sprocess
• Гл. 5 Atomistic kinetic Monte Carlo
diffusion

43. Окисление

Окислительный процесс включает три
этапа:
• Диффузия частиц окислителя (H2O, O2) от
границы раздела газ-окисел через
существующий окисел к границе раздела
кремний-окисел.
• Химическая реакция между окислителем и
кремнием с образованием нового окисла.
• Перемещение материалов и границ раздела
из-за расширения объема, вызванного
образованием оксида.
43

44.

• Уравнения химических реакций:
• Диффузия окислителя описывается законом Фика
и уравнением непрерывности:
где D – коэффициент диффузии окислителя, с –
концентрация и j – поток частиц окислителя.
• Поток окислителя, поступающий из внешней
атмосферы в окисел по нормали к поверхности:
где h – коэффициент массопереноса и c* концентрация окислителя в атмосфере

45. Модель Дила - Гроува

• Скорость роста окисла в одномерном случае
может быть описана моделью Дила – Гроува :
где xox – толщина слоя окисла.
• Уравнение может быть решено аналитически;
параметры модели: константа параболического
роста B и константа линейного роста B/A.
• Более глубокий анализ показывает связь
константы параболического роста с
коэффициентом диффузии, а константы
линейного роста со скоростью химической
реакции.

46. Вывод модели Дила - Гроува

F1 = h(C*-C0) – массоперенос через
внешнюю границу окисла, C*, C0 –
концентрации окисляющих частиц;
F2 = D(C0 – Ci)/x – диффузия
окислителя через окисел к границе
раздела окисел/кремний.
F3 = kCi – химическая реакция на
границе раздела окисел/кремний.
В условиях равновесия
F1 = F2 = F3
F2 = F3 : Ci = C0 /(1 + kx/D)
F1 = F3 : Ci = C*/(1 + k/h + kx/D)
dx/dt = F3 /N
46

47.

F1 = F2 = F3
*
dx kC/N
dt 1 k kx
h
Обозначаем:
В 2D
С*/N Тогда:
1 1
A 2D
k h
D
dx
B
dt A 2x
После интегрирования
x2 +Ax = B(t+t0)
47

48. Модель Массуда

d
x
B
O
X
C
e
x
p
(
xL
/)
O
X
d
t 2
x
A
O
X
• эмпирическая модель, учитывающая ускоренный
рост окисла на начальном этапе окисления
• может рассматриваться как расширение модели
Дила – Гроува; хорошо согласуется с
экспериментом
• параметры L и C зависят от
кристаллографической ориентации и температуры
48

49.

Константы параболического и линейного
роста зависят от давления и температуры
A
B
A
B
2
O
2
H
2
O
H
2
O
A
O
B
B
O
2
H
2
O
В = ВО2 + ВН2О
RP
FP
1
mO
2
O
2
A
P
O
2
O
2
RL
FL
O
2
RP
FP
1
mH
2
O
H
2
O
A
P
H
2
O
H
2
O
RL
FL
H
2
O
ВО2 = FP∙RPO2∙pO2
ВH2О = FP∙RPH2O∙pH2O
49

50. 2D и 3D окисление

• Для точного моделирования необходимо
проводить расчет следующих 2D и 3D
процессов:
– Растворение окислительных реагентов на
границе газ-окисел ,
– Перенос частиц окислителя через
существующий окисел,
– Химическая реакция на границе окиселкремний.
• Растворение и химическая реакция
моделируются как граничные условия;
• Для моделирования переноса
рассчитывается уравнение диффузии
частич в слое окисла
50