Угол между прямыми

1. Угол между прямыми

Угол между прямыми в пространстве можно находить
используя формулу
a1 a2
cos
,
| a1 | | a2 |
где a1 , a2 - направляющие векторы данных прямых.
Однако угол между векторами может быть тупым, а угол
между прямыми нет. Поэтому, если косинус угла между
векторами получился отрицательным, то в ответе нужно
указывать его модуль.
Здесь мы рассмотрим примеры решения задач на
нахождение угла между прямыми в пространстве,
используя указанную выше формулу.

2. Куб 1

В кубе A…D1 найдите угол между прямыми AC и BD1.
Решение. Введем систему координат, считая точку D началом
координат, прямые DA, DC, DD1 – осями координат. Угол между
данными прямыми равен углу между векторами AC ( 1,1, 0) и
BD1( 1, 1,1) . Скалярное произведение этих векторов равно нулю.
Следовательно, эти векторы перпендикулярны.
Ответ. 90о.

3. Куб 2

В кубе A…D1 найдите угол между прямыми AE и BF1,
где E и F1 – середины ребер соответственно BC и C1D1.
Решение. Введем систему координат, считая точку D началом
координат, прямые DA, DC, DD1 – осями координат. Угол между
данными прямыми равен углу между векторами AE ( 0,5,1, 0) и
BF1( 1, 0,5,1). Скалярное произведение этих векторов равно нулю.
Следовательно, эти векторы перпендикулярны.
Ответ. 90о.

4. Куб 3

В кубе A…D1 найдите угол между прямыми AB1 и BC1.
Решение. Введем систему координат,
считая точку D началом координат,
прямые DA, DC, DD1 – осями
координат. Угол между данными
прямыми равен углу между векторами
AB1(0,1,1) и BC1( 1, 0,1). Их
скалярное произведение равно 1. Их
длины равны 2.
Косинус угла между этими векторами равен 0,5.
Ответ. 60о.

5. Куб 4

В единичном кубе A…D1 найдите косинус угла между
прямыми AE и BE1, где E и E1 – середины ребер
соответственно BC и B1C1.
Решение. Введем систему координат,
считая точку D началом координат,
прямые DA, DC, DD1 – осями
координат. Угол между данными
прямыми равен углу между векторами
AE ( 0,5,1, 0) и BE1( 0,5, 0,1). Их
скалярное произведение равно 0,25.
5
.
Их длины равны
2
Косинус угла между этими векторами равен 0,2.
Ответ. 0,2.

6. Пирамида 1

В правильной пирамиде SABCD, все ребра которой равны 1,
найдите угол между прямыми AS и BС.
Решение. Введем систему координат,
считая центр O основания пирамиды
началом координат, прямые OA, OB, OS
– осями координат. Угол между
данными прямыми равен углу между
векторами
2
2
AS
, 0,
2
2
и
2
2
BC
,
, 0 .
2
2
Их скалярное произведение равно 0,5. Их длины равны 1.
Косинус угла между ними равен 0.5.
Ответ: 60о.

7. Пирамида 2

В правильной пирамиде SABCD, все ребра которой равны 1,
найдите угол между прямыми AS и BD.
Решение. Введем систему координат,
считая центр O основания пирамиды
началом координат, прямые OA, OB, OS
– осями координат. Угол между
данными прямыми равен углу между
векторами
2
2
AS
, 0,
2
2
и BD 0, 2, 0 .
Их скалярное произведение равно 0. Следовательно, угол между
ними равен 90о
Ответ: 90о.

8. Пирамида 3

В правильной пирамиде SABCD, все ребра которой равны 1, точка E
– середина ребра SC. Найдите косинус угла между прямыми AS и
BE.
Решение. Введем систему координат,
считая центр O основания пирамиды
началом координат, прямые OA, OB, OS
– осями координат. Угол между
данными прямыми равен углу между
векторами
2
2
AS
, 0,
2
2
2
2 2
и BE , , .
2 4
4
Их скалярное произведение равно 0,5. Их длины равны 1 и 3 .
2
3
Косинус угла между ними равен
.
3
3
Ответ:
.
3

9. Пирамида 4

В правильной пирамиде SABCD, все ребра которой равны
1, точки E, F – середины ребер SB и SC. Найдите косинус
угла между прямыми AE и BF.
Решение. Введем систему координат,
считая центр O основания пирамиды
началом координат, прямые OA, OB, OS
– осями координат. Угол между
данными прямыми равен углу между
векторами
2 2 2 и BF 2 , 2 , 2 .
AE
,
,
4
2
4
2 4 4
1
Их скалярное произведение равно . Их длины равны
1 8
Косинус угла между ними равен .
6
1
Ответ: .
6
3
.
2

10. Пирамида 5

В правильной пирамиде SABCDEF, стороны основания
которой равны 1, а боковые ребра равны 2, точки G и H –
середины ребер SB и SC. Найдите косинус угла между
прямыми AG и BH.
Решение. Введем систему координат,
считая центр O основания пирамиды
началом координат, прямые OA, OP, OS
– осями координат. Угол между
данными прямыми равен углу между
векторами
1 3 3
AG ,
,
4
4
2
3
3 3
и BH , , .
4 2
4
Их скалярное произведение равно 3 . Их длины равны 1.
3
Косинус угла между ними равен .
4
3
Ответ: .
4
4

11. Призма 1

В правильной 3-й призме ABCA1B1C1, ребра которой
равны 1, найдите косинус угла между прямыми AB1 и BC1.
Решение. Введем систему координат,
считая середину D ребра AC началом
координат, прямые DA, DB, DD1 –
осями координат. Угол между данными
прямыми равен углу между векторами
1 3
AB1 ,
,1
2
2
и
1
3
BC1 ,
,1 .
2
2
Их скалярное произведение равно 0,5, Длины равны
угла между ними равен 0,25.
Ответ. 0,25.
2 . Косинус

12. Призма 2

В правильной 6-й призме A…F1, ребра которой равны 1,
найдите угол между прямыми AС1 и BE.
Решение. Введем систему координат,
считая центр O основания призмы
началом координат, прямые OA, OG,
OO1 – осями координат. Угол между
данными прямыми равен углу между
векторами
3 3
AC1 ,
,1
2
2
и BE 1, 3, 0 .
Их скалярное произведение равно 0. Угол между ними равен 90о.
Ответ. 90о.

13. Призма 3

В правильной 6-й призме A…F1, ребра которой равны 1,
найдите угол между прямыми AB1 и BE1.
Решение. Введем систему координат,
считая центр O основания призмы
началом координат, прямые OA, OG,
OO1 – осями координат. Угол между
данными прямыми равен углу между
векторами
1 3
AB1 ,
,1
2
2
и BE1 1, 3,1 .
Их скалярное произведение равно 0. Угол между ними равен 90о.
Ответ. 90о.

14. Призма 4

В правильной 6-й призме A…F1, ребра которой равны 1,
найдите косинус угла между прямыми AB1 и BD1.
Решение. Введем систему координат,
считая центр O основания призмы
началом координат, прямые OA, OG,
OO1 – осями координат. Угол между
данными прямыми равен углу между
векторами
1 3
AB1 ,
,1
2
2
и
3
3
BD1 ,
,1 .
2
2
Их скалярное произведение равно 1. Длины равны
Косинус угла между ними равен 2 .
4
2
Ответ.
.
4
2 и 2.

15. Призма 5

В правильной 6-й призме A…F1, ребра которой равны 1,
найдите косинус угла между прямыми AC1 и BD1.
Решение. Введем систему координат,
считая центр O основания призмы
началом координат, прямые OA, OG,
OO1 – осями координат. Угол между
данными прямыми равен углу между
векторами
3 3
AC1 ,
,1
2
2
и
3
3
BD1 ,
,1 .
2
2
Их скалярное произведение равно 2,5. Длины равны 2.
Косинус угла между ними равен 5 .
8
5
Ответ. .
8

16. Многогранник 1

Для многогранника, изображенного на рисунке, все
двугранные углы которого прямые, найдите косинус
угла между прямыми AC и BС2.
Решение. Введем систему координат,
считая точку D началом координат,
прямые DA, DC, DD2 – осями
координат. Угол между данными
прямыми равен углу между векторами
AC ( 2, 2, 0) и BC2 ( 2, 1, 2) .
Скалярное произведение этих векторов
равно 2, их длины равны 2 2 и 3.
Ответ.
2
.
6
2
Косинус угла между ними равен
.
6

17. Многогранник 2

Для многогранника, изображенного на рисунке, все
двугранные углы которого прямые, найдите косинус
угла между прямыми AC1 и B1D2.
Решение. Введем систему координат,
считая точку D началом координат,
прямые DA, DC, DD2 – осями
координат. Угол между данными
прямыми равен углу между векторами
AC1( 2, 2,1) и B1D2 ( 2, 2,1) .
Скалярное произведение этих векторов
равно 1, их длины равны 3.
Ответ.
1
.
9
1
Косинус угла между ними равен
9
.

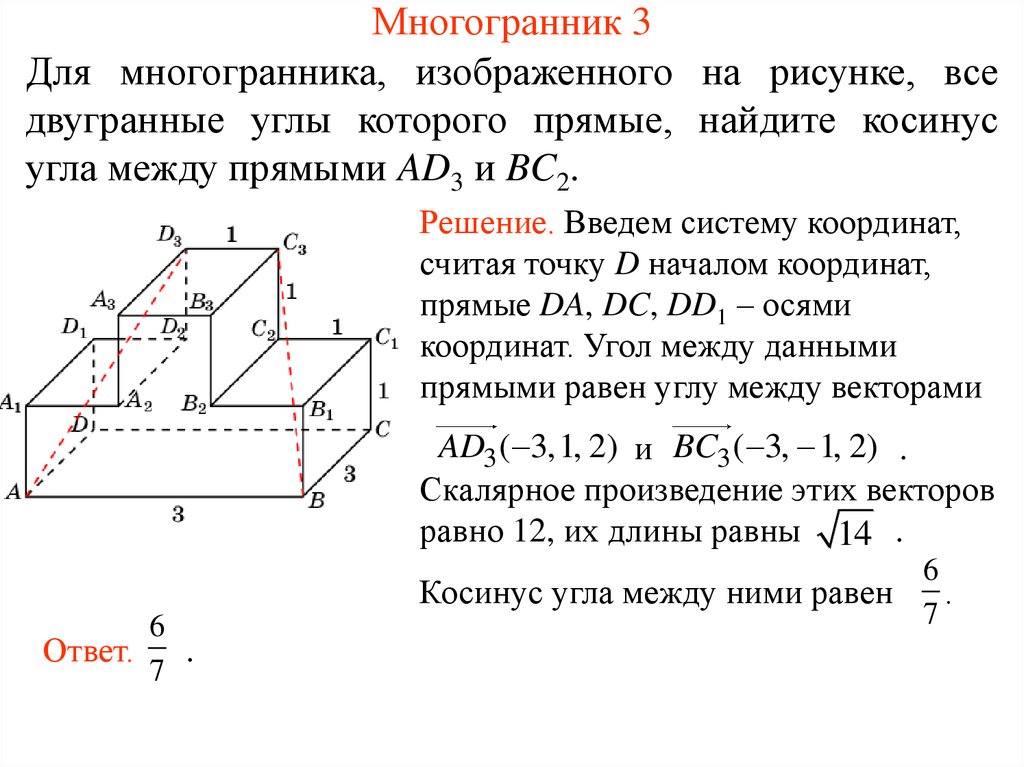
18. Многогранник 3

Для многогранника, изображенного на рисунке, все
двугранные углы которого прямые, найдите косинус
угла между прямыми AD3 и BC2.
Решение. Введем систему координат,
считая точку D началом координат,
прямые DA, DC, DD1 – осями
координат. Угол между данными
прямыми равен углу между векторами
AD3 ( 3,1, 2) и BC3 ( 3, 1, 2) .
Скалярное произведение этих векторов
равно 12, их длины равны 14 .
6
Ответ.
.
7
6
Косинус угла между ними равен
.
7

19. Многогранник 4

Для многогранника, изображенного на рисунке, все
двугранные углы которого прямые, найдите угол между
прямыми BC2 и DD2.
Решение. Введем систему координат,
считая точку F началом координат,
прямые FA, FE, FD2 – осями координат.
Угол между данными прямыми равен
углу между векторами
BC2 ( 2, 0, 2) и DD2 ( 1, 2, 2) .
Скалярное произведение этих векторов
равно 6, их длины равны 2 2 и 3 .
Ответ. 45о.
2
Косинус угла между ними равен
.
2