Similar presentations:
Введение в метод координат. Выбор системы координат. Координаты точки. Уравнение плоскости по трем точкам
1. Введение в метод координат
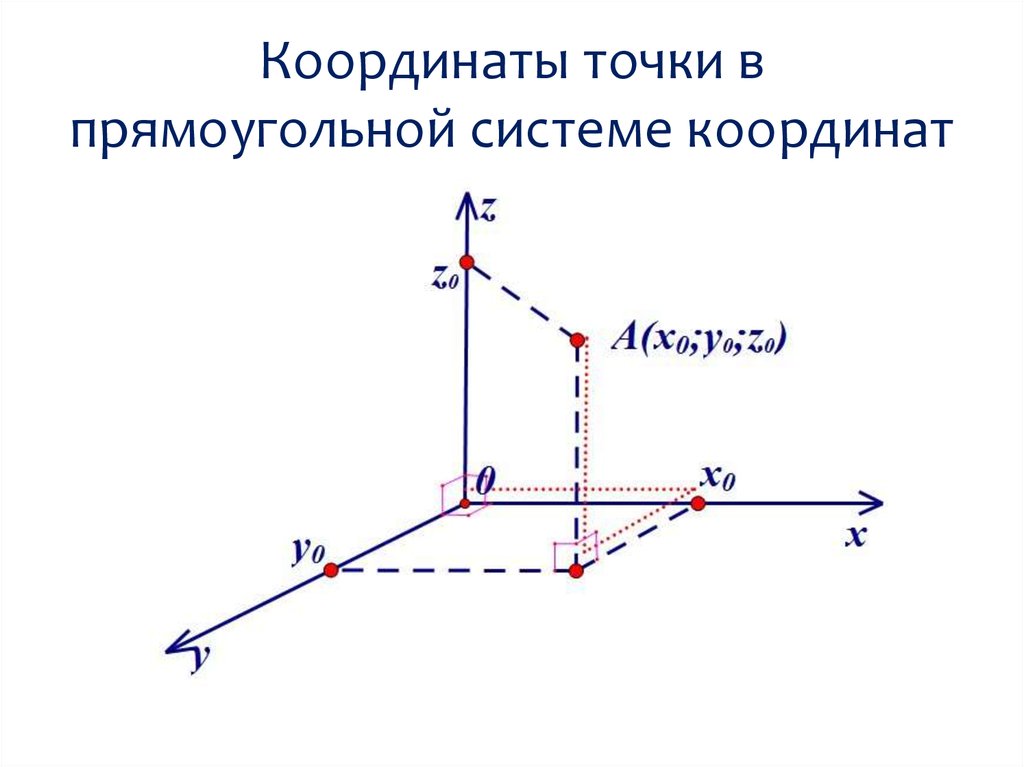
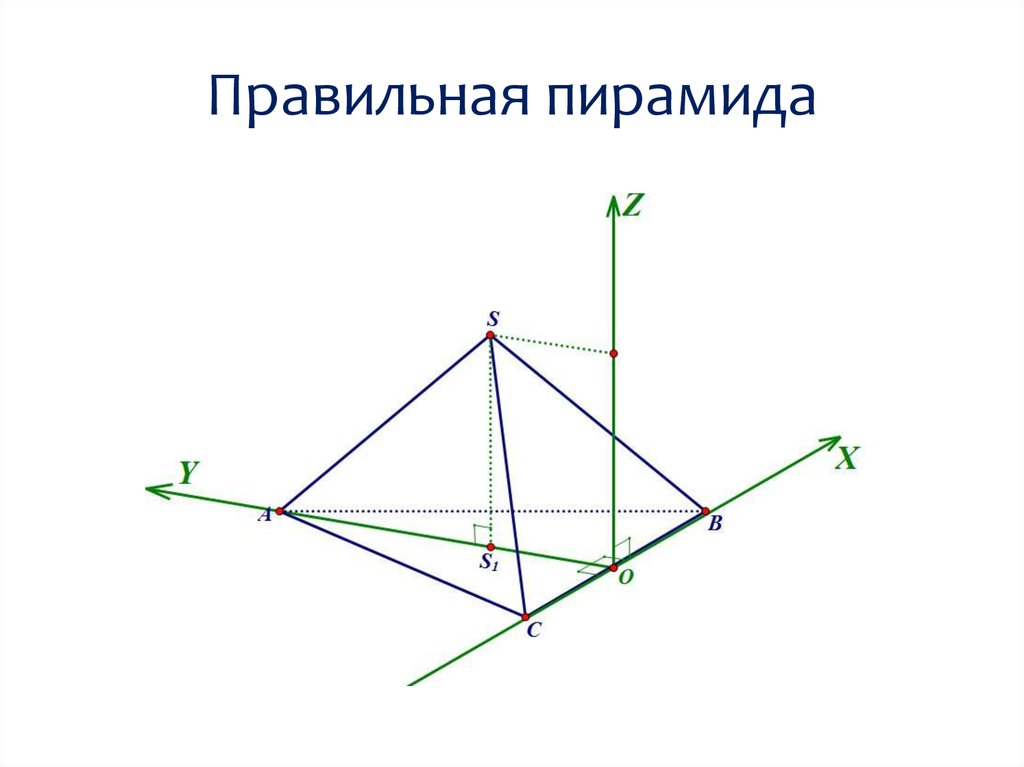
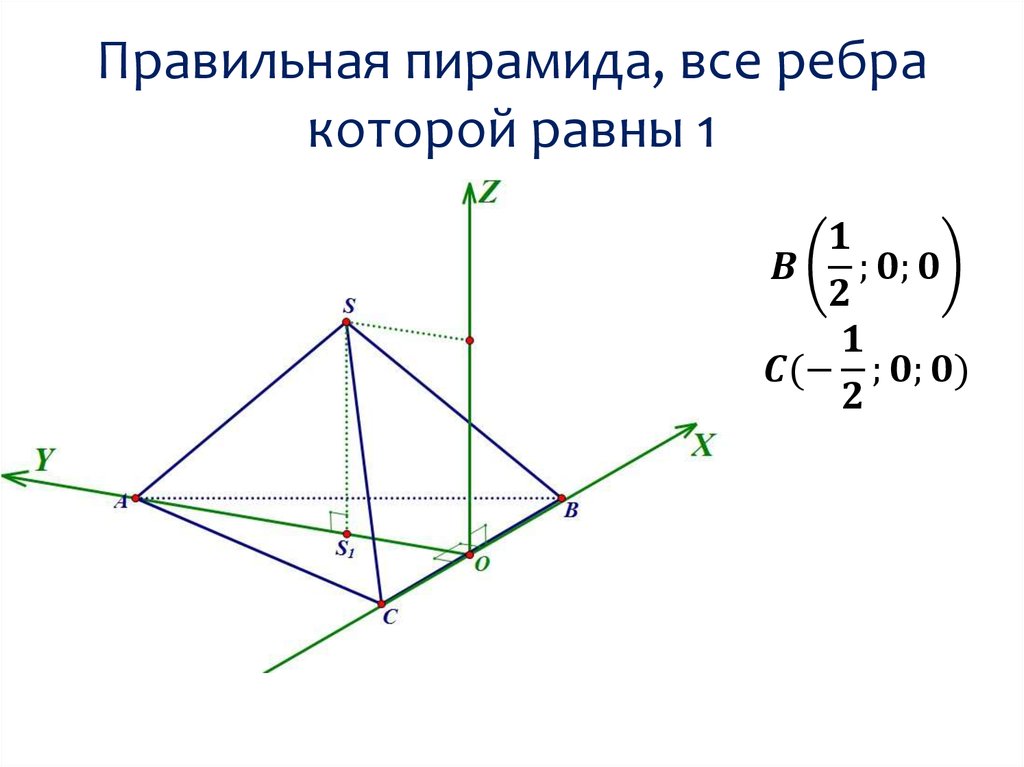
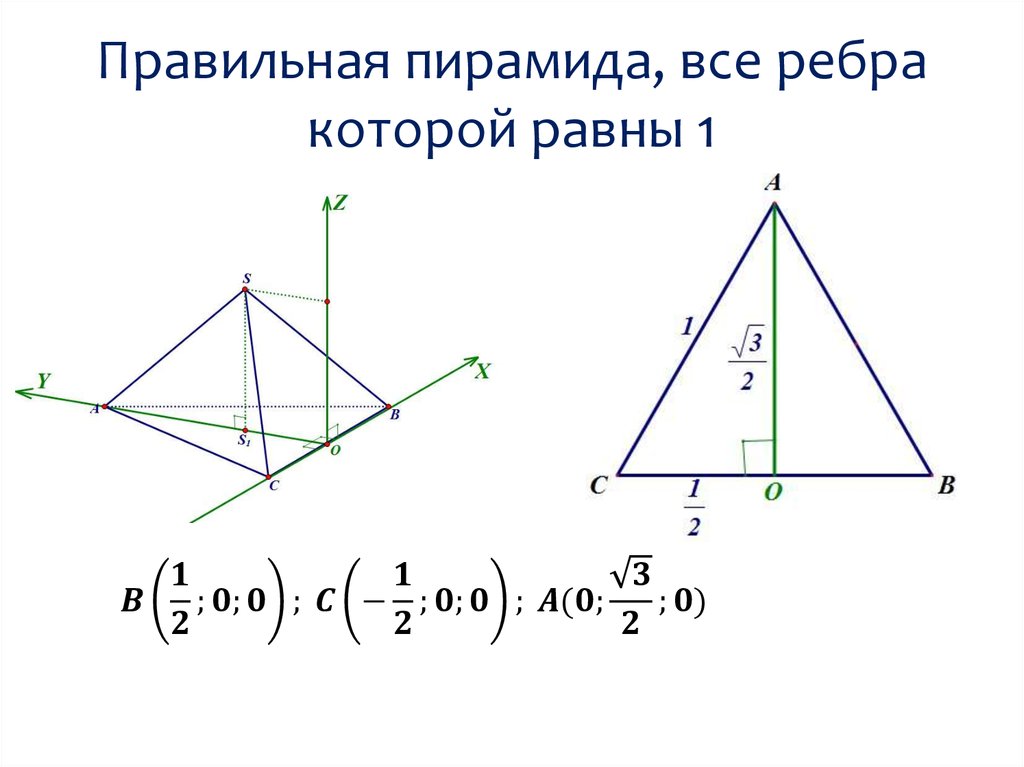
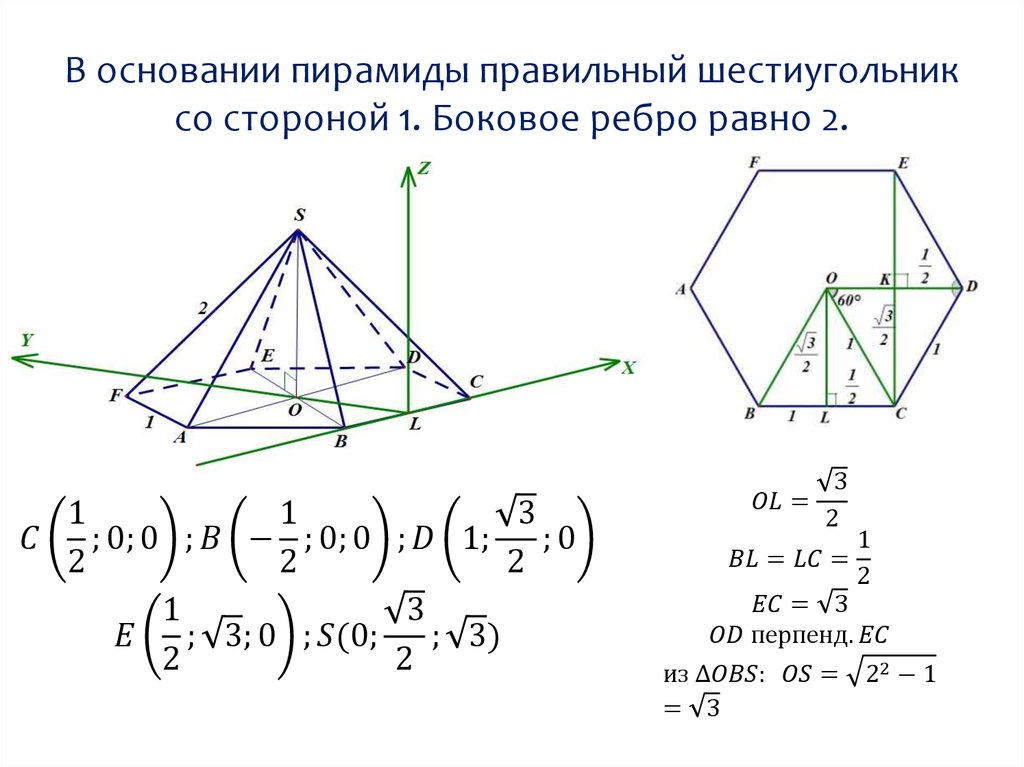
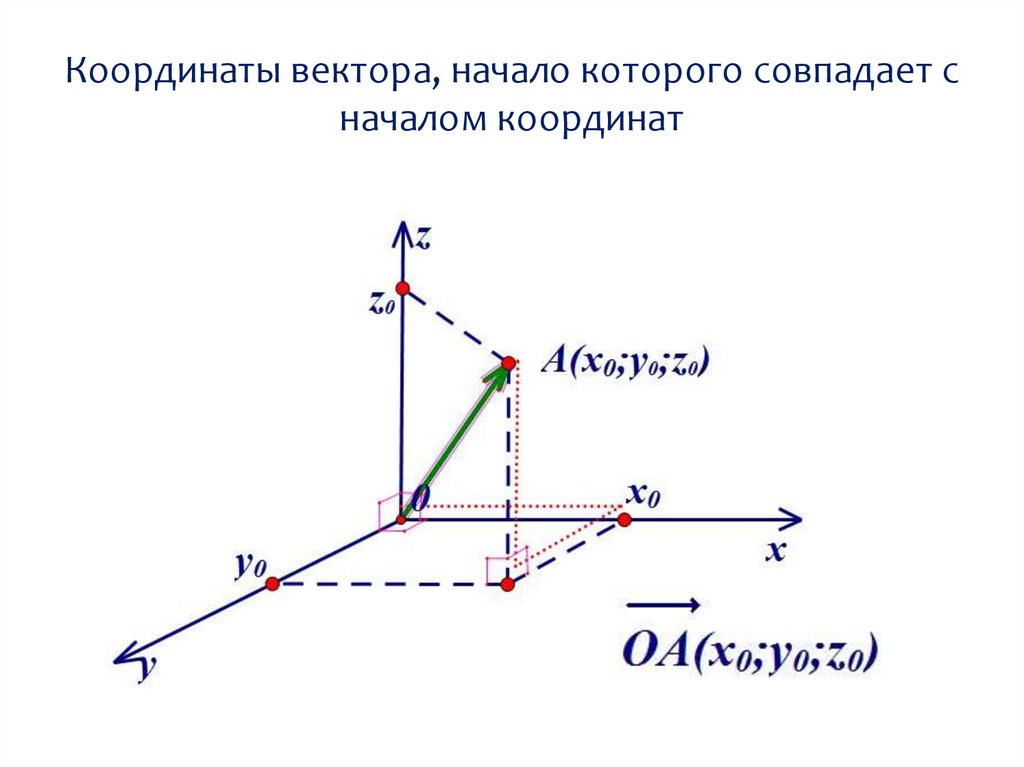
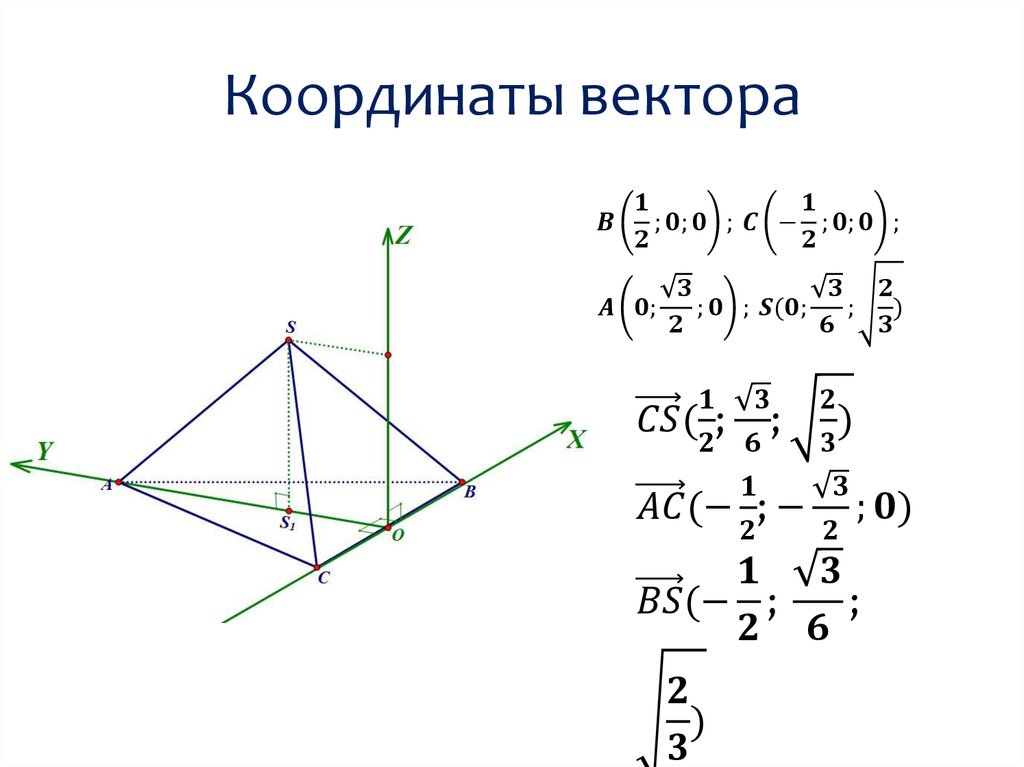
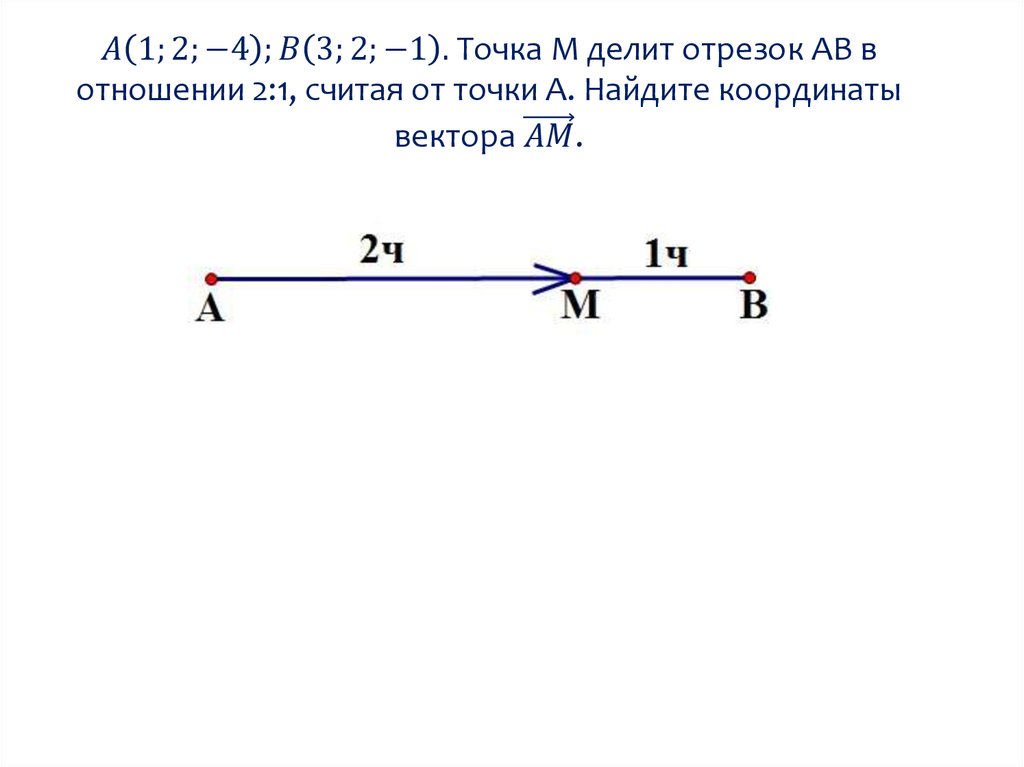
Выбор системы координатКоординаты точки
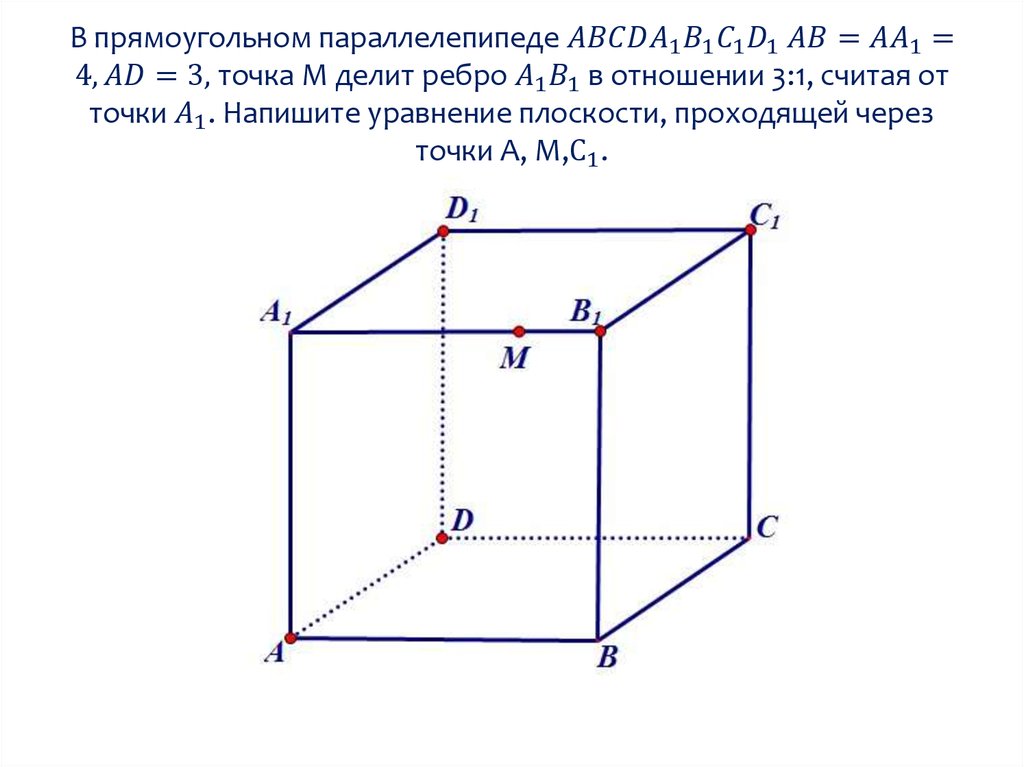
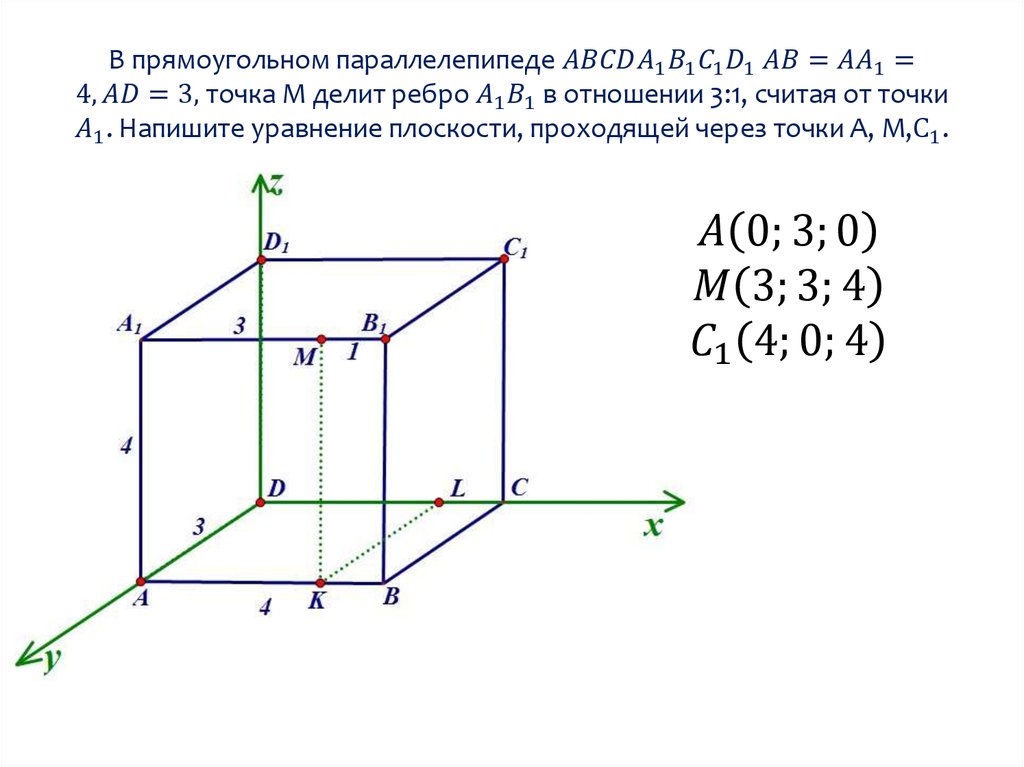
Уравнение плоскости по трем точкам
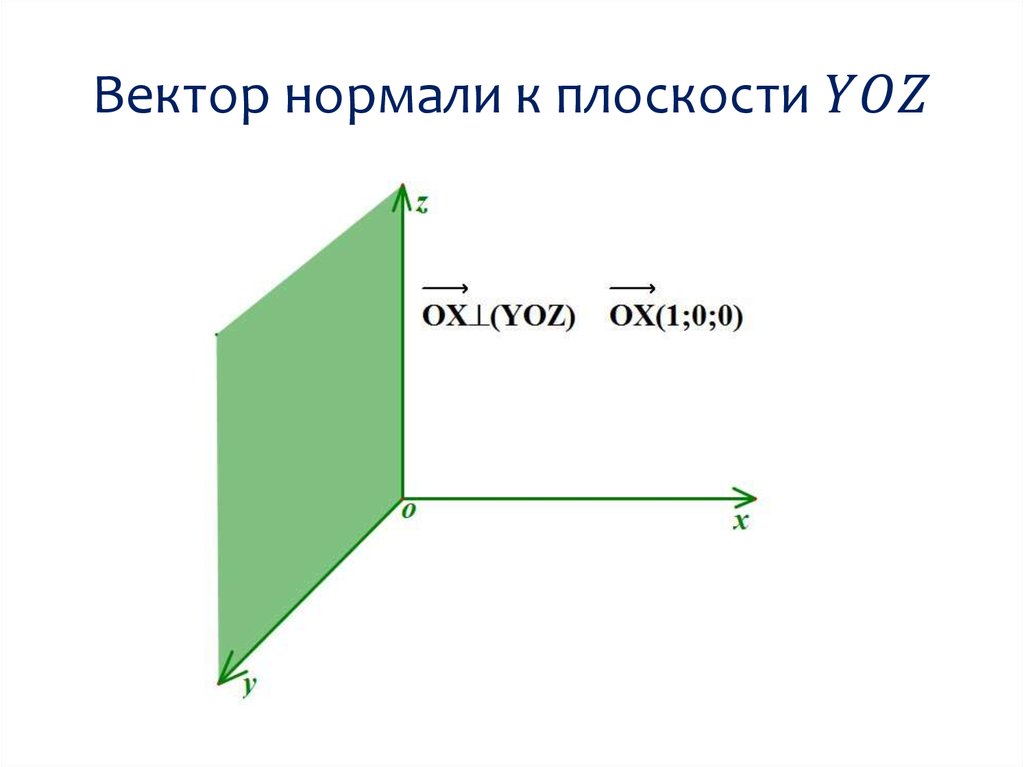
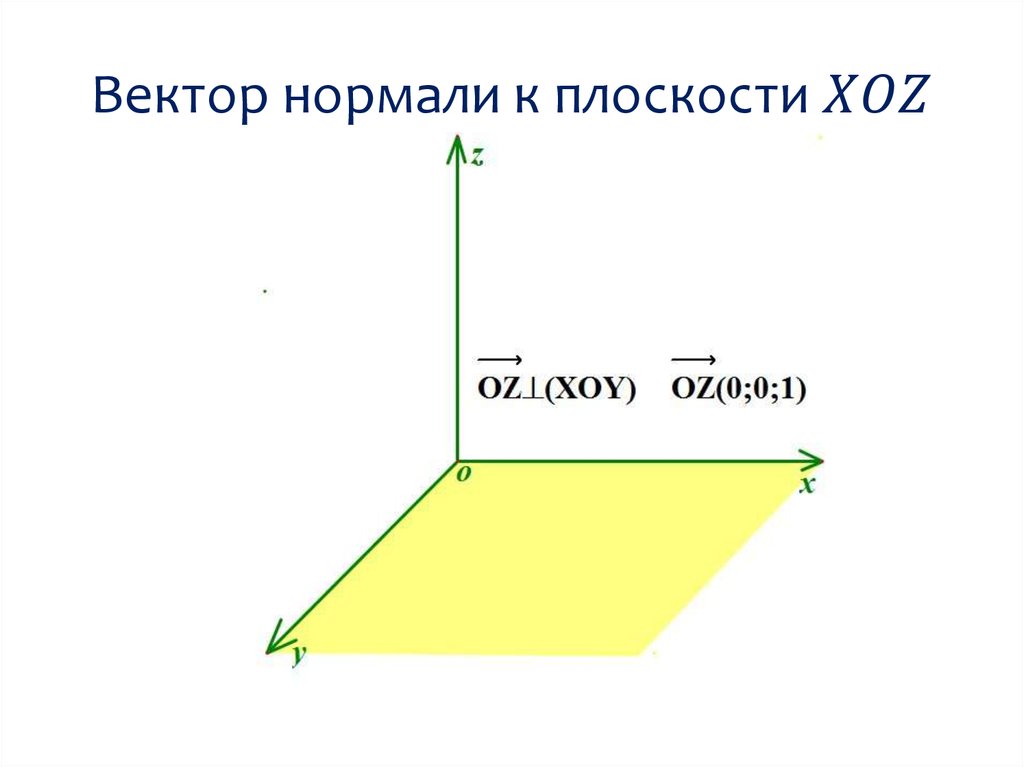
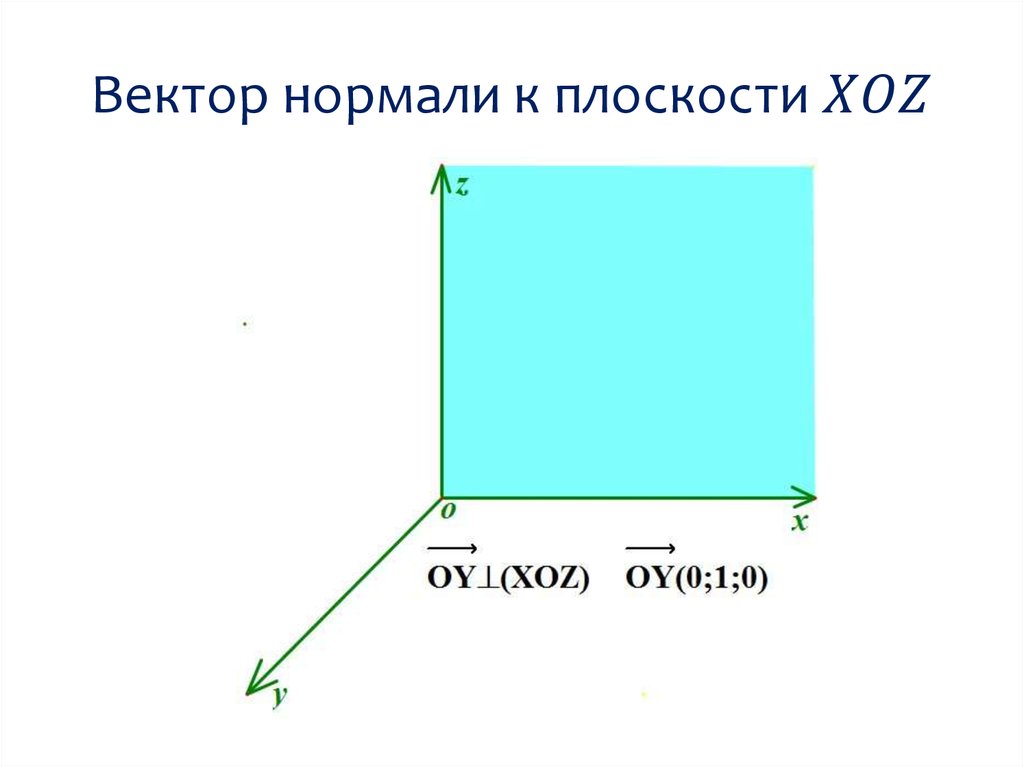
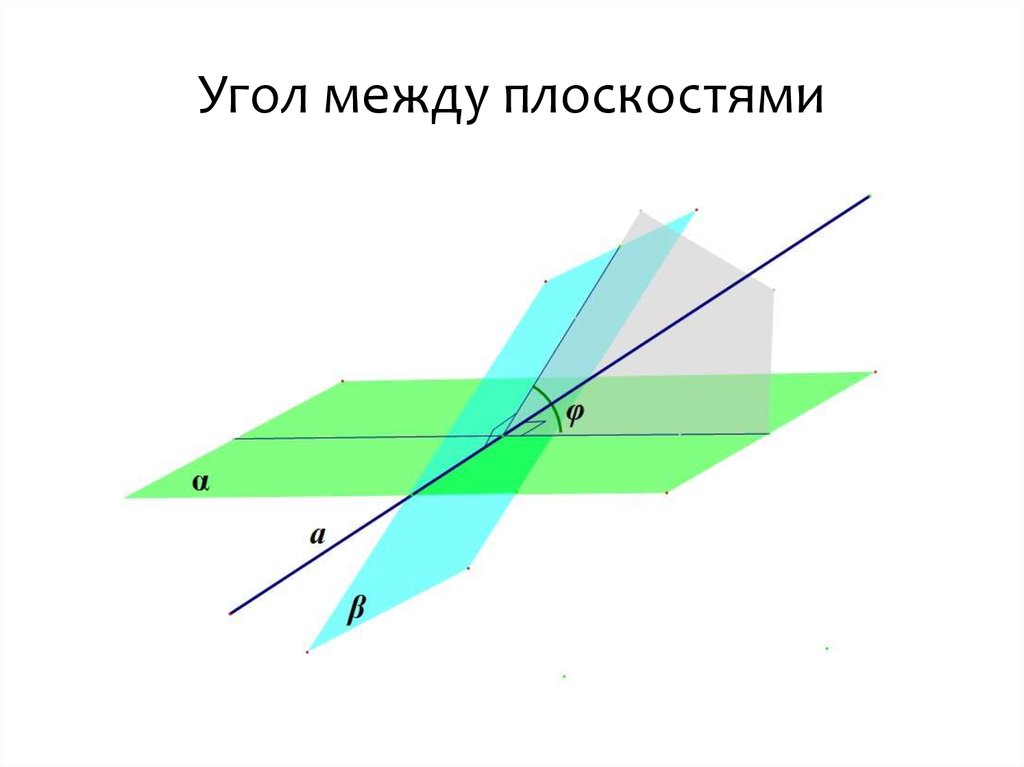
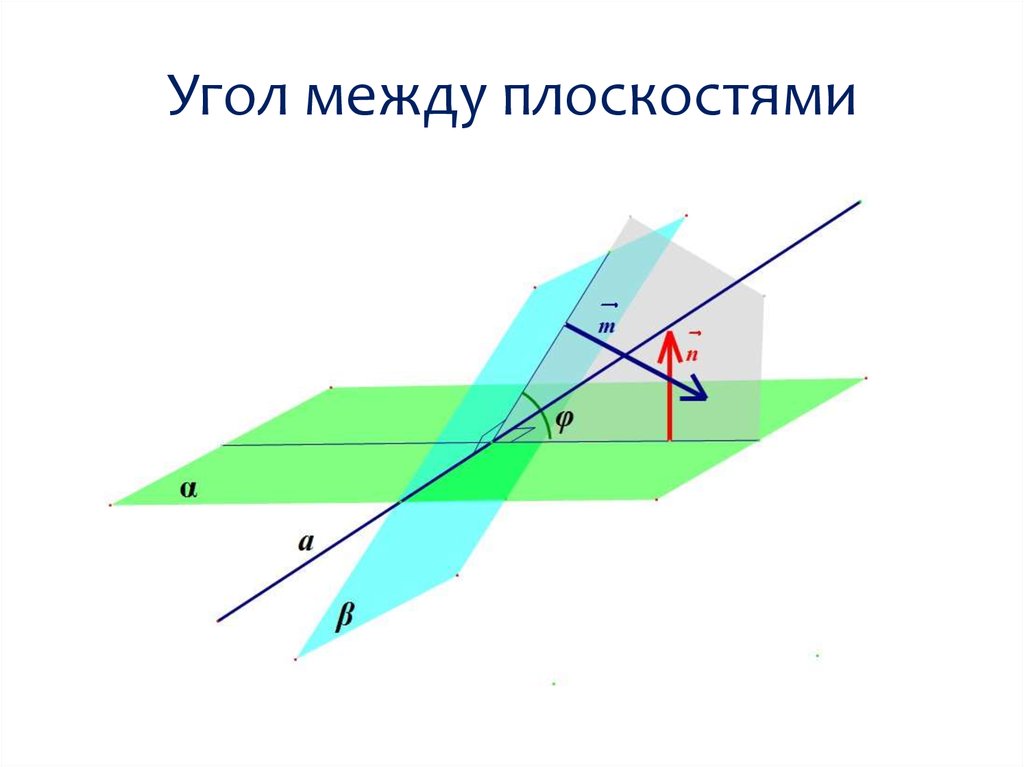
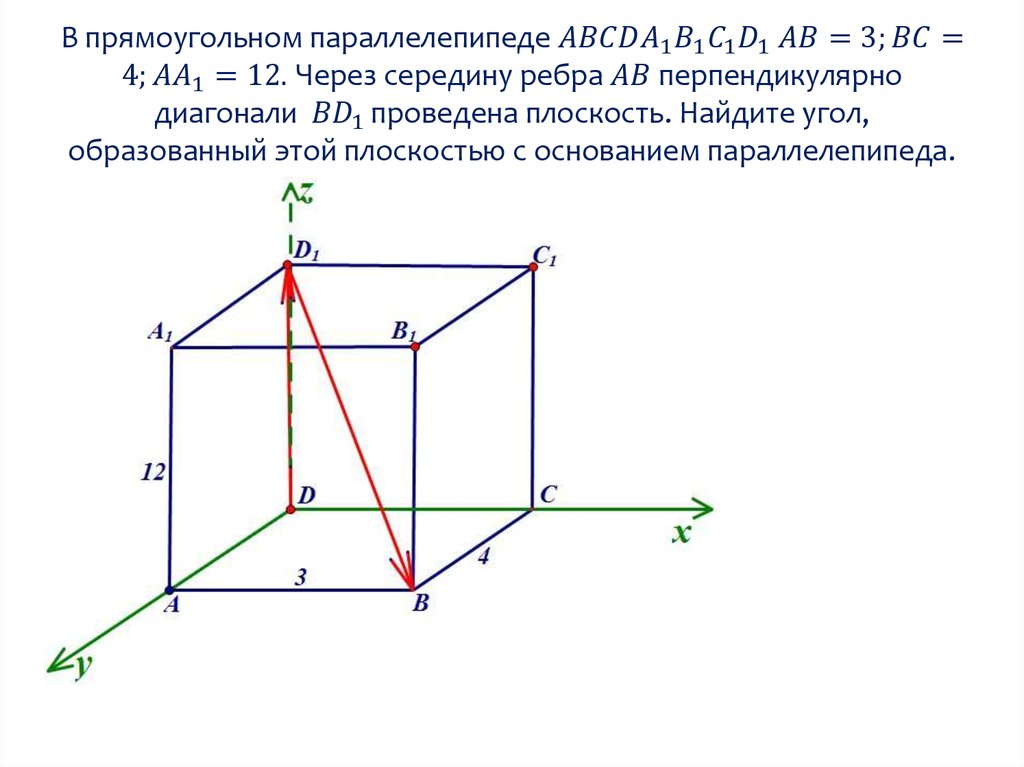
Вектор нормали к плоскости
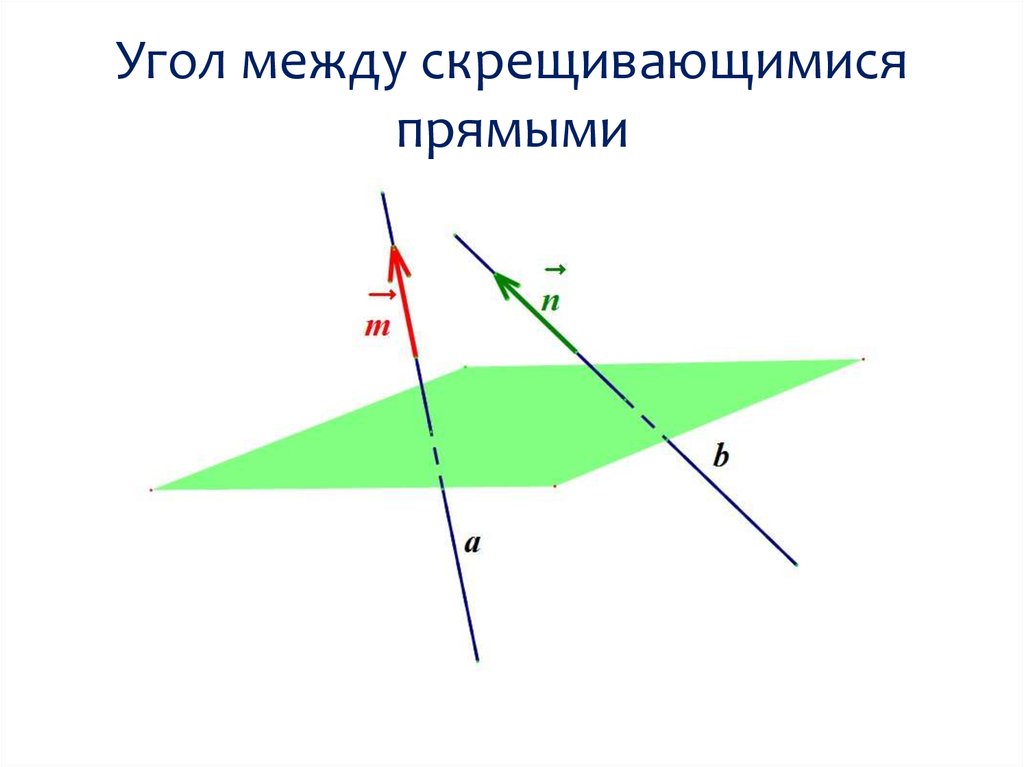
Направляющий вектор прямой


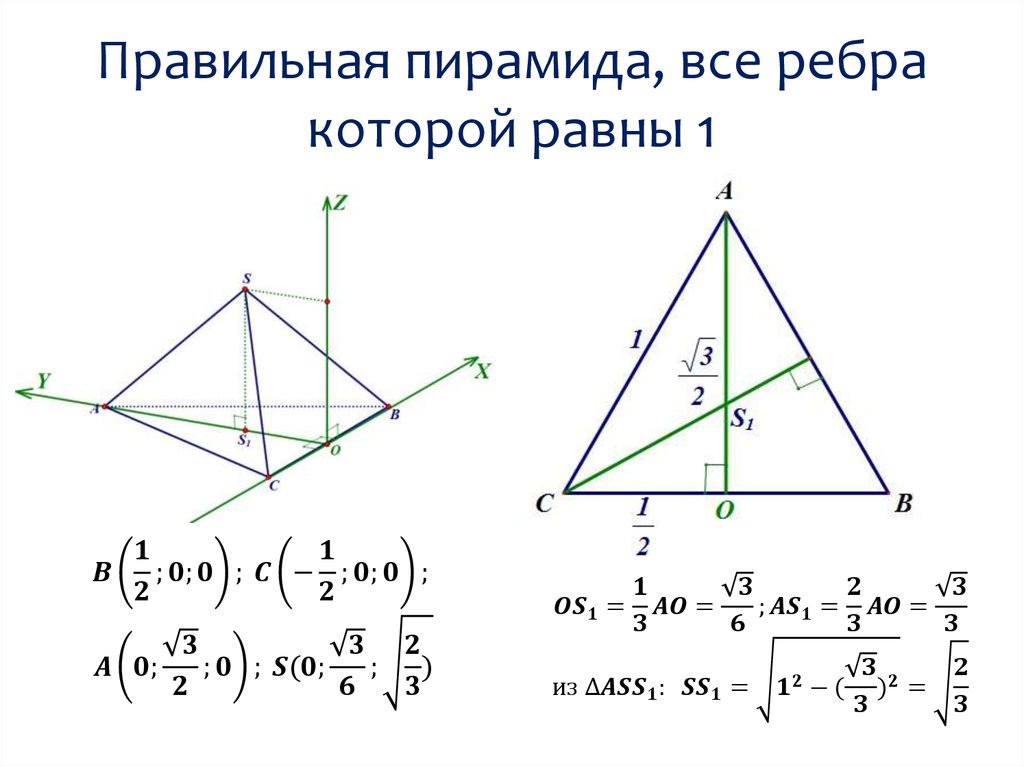
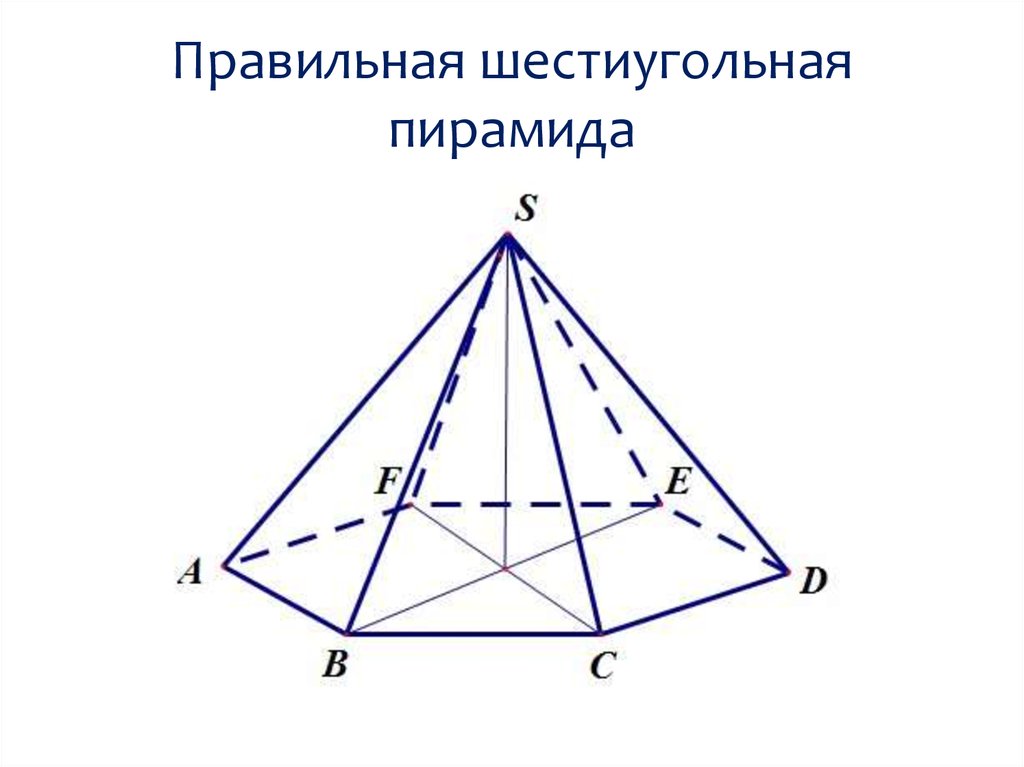
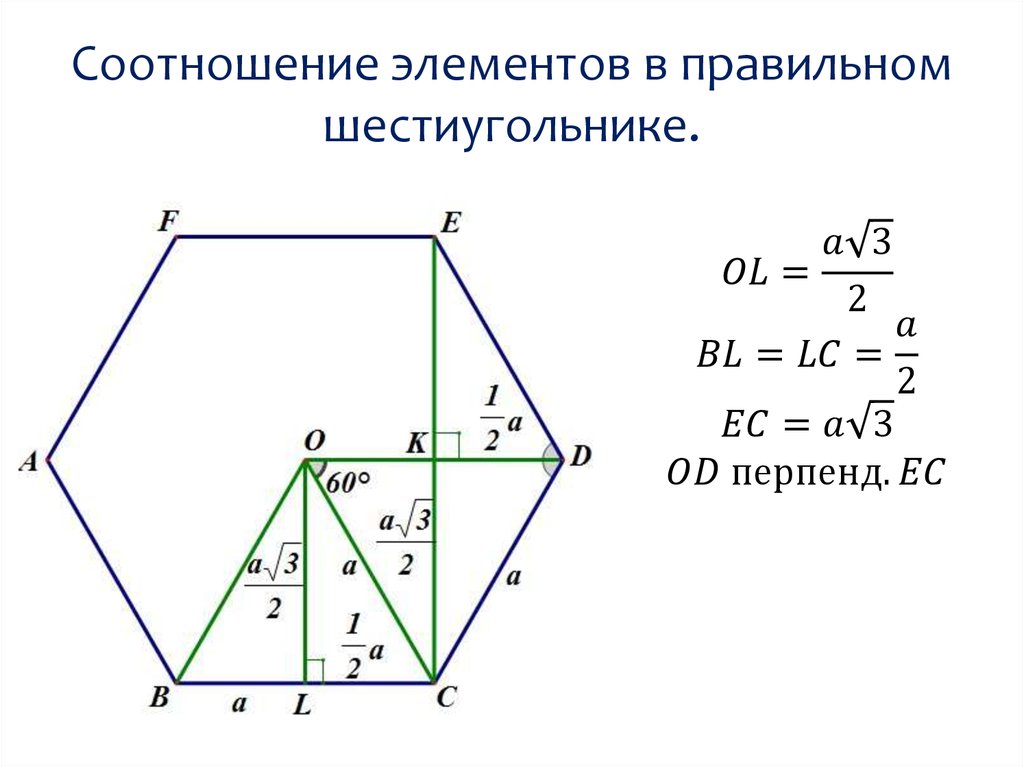
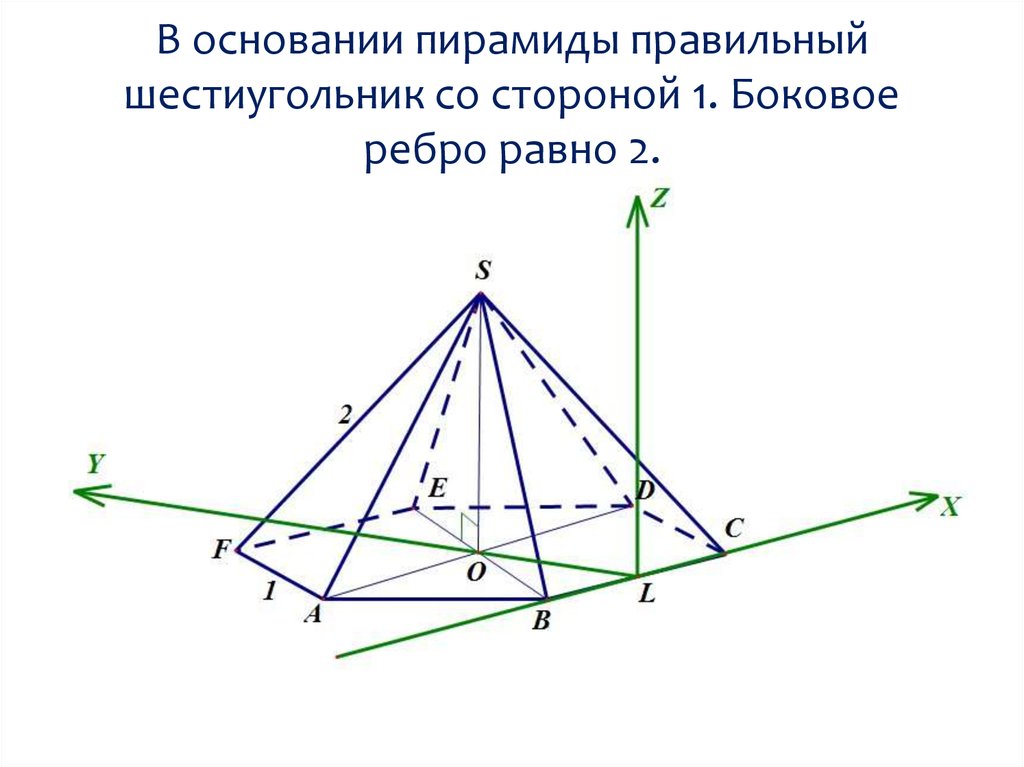

























 mathematics
mathematics








