Погрешность и точность приближения

1. Погрешность и точность приближения

2. Округлите число до десятых:

0,124
7,
05
6,1298
12,56
81,97
82,0
0,1
7,1
6,1
Правильный ответ: 12,6

3. Округлите число до сотен:

5985
246,3
15049
7051
86
Правильный ответ:
15000
7100
100
6000
200

4. Округлите число

до
до
додесятков:
тысячных:
единиц:
сотых:
156,3782 ≈ 156,38
156,378
156,4
156
160

5. Числа

6. Приближенное и точное число всегда отличаются друг от друга.

При приближении всегда возникает
некоторая погрешность приближения.
В математике различают:
Абсолютную погрешность
Относительную погрешность

7. Прописной буквой Δ обозначают абсолютную погрешность измерения Строчной буквой δ - относительную погрешность измерения

Прописной буквой Δ
обозначают абсолютную
погрешность измерения
Строчной буквой δ относительную погрешность
измерения

8. Абсолютная погрешность приближения

Абсолютной погрешностью приближения
называется модуль разности между истинным
значением величины и её приближённым
значением.
x a
x
a
— истинное значение,
— приближённое.

9.

Относительная
погрешность приближения
x a
a
x
a

10. Пример. Найти абсолютную и относительную погрешность числа с точностью до единиц.

При округлении числа 24,3 до единиц получается число
24.
Абсолютная погрешность:
24,3 24 0,3
Относительная погрешность:
0,3
24
0,0125
Говорят, что относительная погрешность в этом случае
равна 1,25%.

11.

х а абсолютная погрешность
х а
а
относительная погрешность

12.

198 200 2
2 абсолютная погрешность
198 200
2
200
200
2
*100% 1% относительная погрешность
200

13. Заполните таблицу:

№
Число
Приближенное
значение
Абсолютная
погрешность
Относительная
погрешность
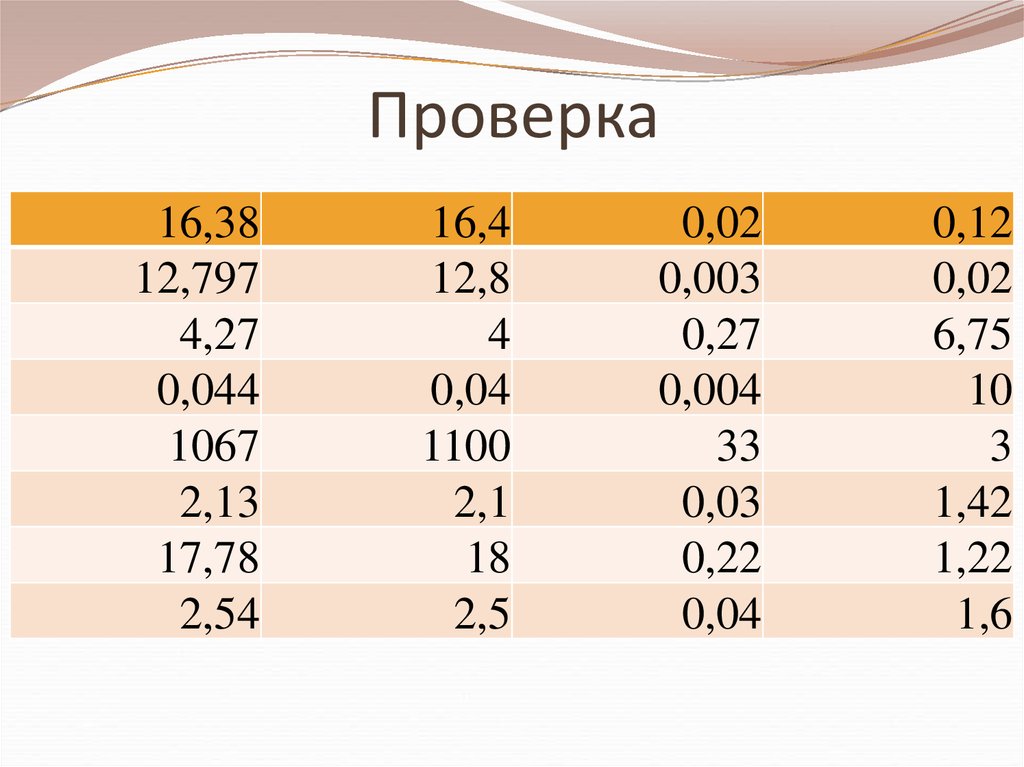
Старинные русские меры массы:
а) пуд - 16,38 кг (до десятых)
б) лот -12,797 г (до сотых)
в) золотник - 4,27 г (до целых)
г) доля - 0,044 г (до сотых)
Старинная русская мера длины:
д) верста - 1067м (до сотен)
е) сажень - 2,13м (до десятых)
ж) пядь -17,78 cм (до целых)
з) дюйм - 2,54 см (до десятых)

14. Проверка

16,38
12,797
4,27
0,044
1067
2,13
17,78
2,54
16,4
12,8
4
0,04
1100
2,1
18
2,5
0,02
0,003
0,27
0,004
33
0,03
0,22
0,04
0,12
0,02
6,75
10
3
1,42
1,22
1,6

15.

Если х≈а и абсолютная погрешность этого
приближенного значения не превосходит некоторого
числа h, то число а называют приближенным
значением х с точностью до h.
Пишут х≈а с точностью до h. Используют также и
такую запись: х=а±h, эта запись означает, что точное
значение переменной х заключено между числами аh и а+h, а-h ≤ х ≤ а+h.
На пример, на рулоне обоев написано, что его длина
равна 18 ± 0,3 м. значит, если L-истинное значение
длины рулона (в метрах), то
18-0,3 ≤ L ≤ 18+0,3
17,7 ≤ L ≤ 18,3