Построение функции мультивариантного спроса

1.

Построение функции мультивариантного спроса
Сказка
о тестировании и оценке результатов
построения множественной регрессии

2.

Шаг 1. Тестирование пригодности модели
Знаки коэффициентов
Величины параметров

3.

Знак параметра указывает
направление изменения переменной
спроса по отношению к изменению
независимой переменной
Положительный знак:
0,009
Отрицательный знак:
Переменная спроса изменяется в том же
направлении, что и независимая
переменная
Переменная спроса и независимая
переменная изменяются в
противоположных направлениях
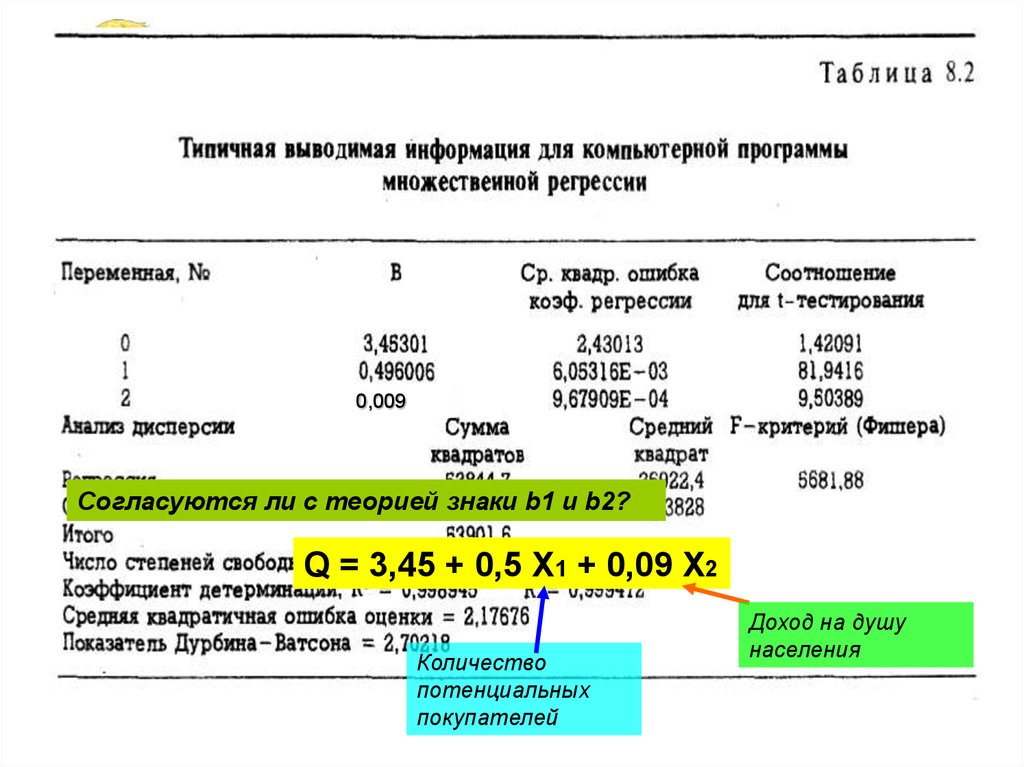
Согласуются ли с теорией знаки b1 и b2?
Q = 3,45 + 0,5 X1 + 0,09 X2
Количество
потенциальных
покупателей
Доход на душу
населения

4.

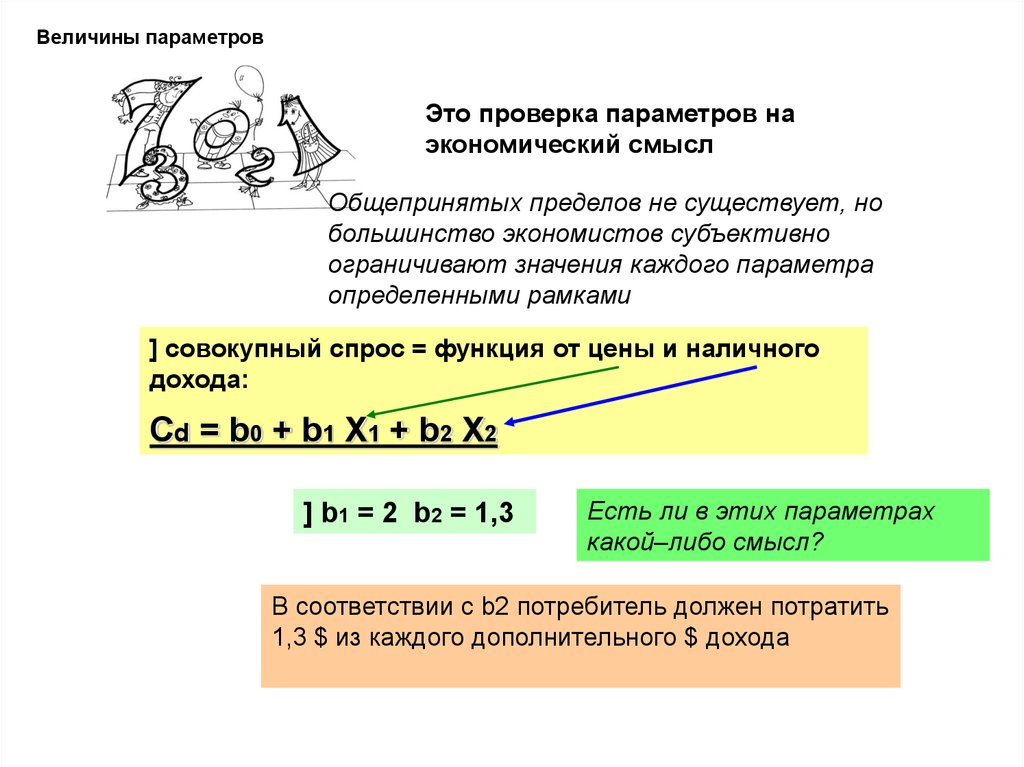
Величины параметров
Это проверка параметров на
экономический смысл
Общепринятых пределов не существует, но
большинство экономистов субъективно
ограничивают значения каждого параметра
определенными рамками
] совокупный спрос = функция от цены и наличного
дохода:
Cd = b0 + b1 X1 + b2 X2
] b1 = 2 b2 = 1,3
Есть ли в этих параметрах
какой–либо смысл?
В соответствии с b2 потребитель должен потратить
1,3 $ из каждого дополнительного $ дохода

5.

Шаг 2. Статистические тесты и оценки
Общие тесты
Множественный коэффициент детерминации, R^2
Скорректированный множественный коэффициент
детерминации, R^2
F – статистика для регрессии
Средняя квадратичная ошибка оценки для регрессии

6.

Шаг 2.
Статистические тесты и оценки
Общие тесты
Множественная регрессия описывает регрессионную
плоскость и наблюдаемые точки лежат выше, ниже и
на этой плоскости
Множественный коэффициент детерминации, R^2
Является мерой того, насколько хорошо плоскость,
описываемая регрессионным уравнением, удовлетворяет
экспериментальным данным
^
^
(
Q
Q
)
(
Q
Q
)
(
Q
Q
)
i
i
i
2
2
2
i
Полная вариация = Объяснимая вариация + Необъяснимая вариация
Вариация – это сумма квадратов отклонений наблюдаемых значений от линии регрессии
Коэффициент имеет исключительно математический смысл и
не определяет никакой причинно-следственной связи
R^2 = полная объяснимая вариация/полная вариация =
^
(Qi Q)2
(Qi Q)2
6

7.

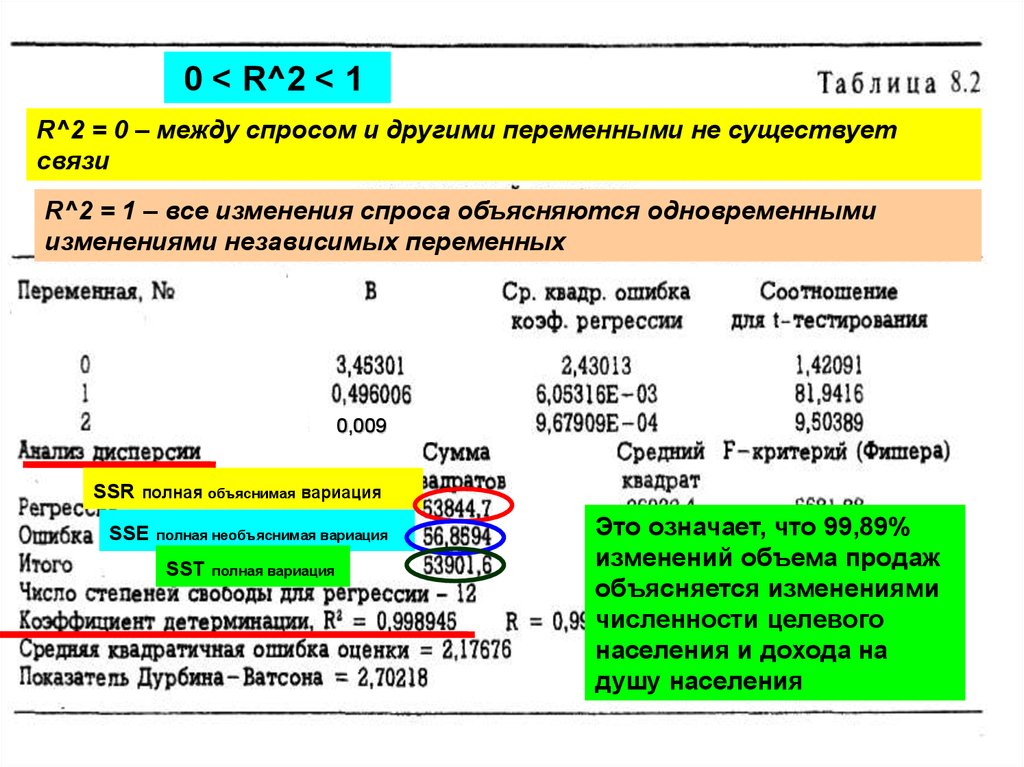
0 < R^2 < 1
R^2 = 0 – между спросом и другими переменными не существует
связи
R^2 = 1 – все изменения спроса объясняются одновременными
изменениями независимых переменных
0,009
SSR полная объяснимая вариация
SSЕ
полная необъяснимая вариация
SSТ
полная вариация
Это означает, что 99,89%
изменений объема продаж
объясняется изменениями
численности целевого
населения и дохода на
душу населения

8.

Шаг 2.
Статистические тесты и оценки
Общие тесты
Скорректированный множественный коэффициент
детерминации, R^2
Чтобы получить информативные результаты, количество наблюдений должно быть
достаточным для того, чтобы переменная спроса имела некоторую свободу изменений
Уделяет должное внимание степеням свободы, определяемым
количеством наблюдений и количеством параметров
k 2
R
R
1
R
n
k
1
2
2
Количество наблюдений
Количество независимых переменных
8

9.

Приемлемые значения
R2
?
Обычно если количество наблюдений в три или четыре
раза больше количества независимых переменных, то
приемлемым считается
R2 0,75

10.

Шаг 2.
Статистические тесты и оценки
Общие тесты
F – тестирование на полную значимость
Показывает статистическую значимость объяснимой вариации
F=
(полная объяснимая вариация)/k
=
(полная необъяснимая вариация)/ (n-k-1)
2
^ -Q
(
Q
)
i /k
2
^ )
(
Q
-Q
/n
k
1
i
i
Количество наблюдений
Количество независимых переменных
F – тест основан
наFтом,
что дляиспользуется
статистической
Расчетное
значение
– критерия
для
Если
гипотеза
верна,
то
не
существует
действительной
значимости
регрессионного
уравнения
по
крайней
мере
проверки нулевой гипотезы о том, что все истинные
связи
зависимой
и независимой
один между
из истинных
параметров
регрессии
должен быть
регрессионные
параметры
равны
нулюпеременными
не равен 0

11.

F – тестирование на полную значимость
F=
(полная объяснимая вариация)/k
=
(полная необъяснимая вариация)/ (n-k-1)
2
^ -Q
(
Q
)
i /k
2
^ )
(
Q
-Q
/n
k
1
i
i
Количество наблюдений
Количество независимых переменных
Значение F – критерия устанавливает верхний предел
значений F, которые возможны в случае выполнения нулевой
гипотезы
Это значение известно как критическое значение F - распределения
Если расчетное значение F превышает 3,49 (к = 3, n-k-1 = 12), то
на 95% (уровень значимости 0,05) коэффициенты регрессии не
равны нулю

12.

0,009
Нулевая гипотеза отвергнута
Регрессия в целом статистически
значима на уровне 0,05

13.

Шаг 2.
Статистические тесты и оценки
Общие тесты
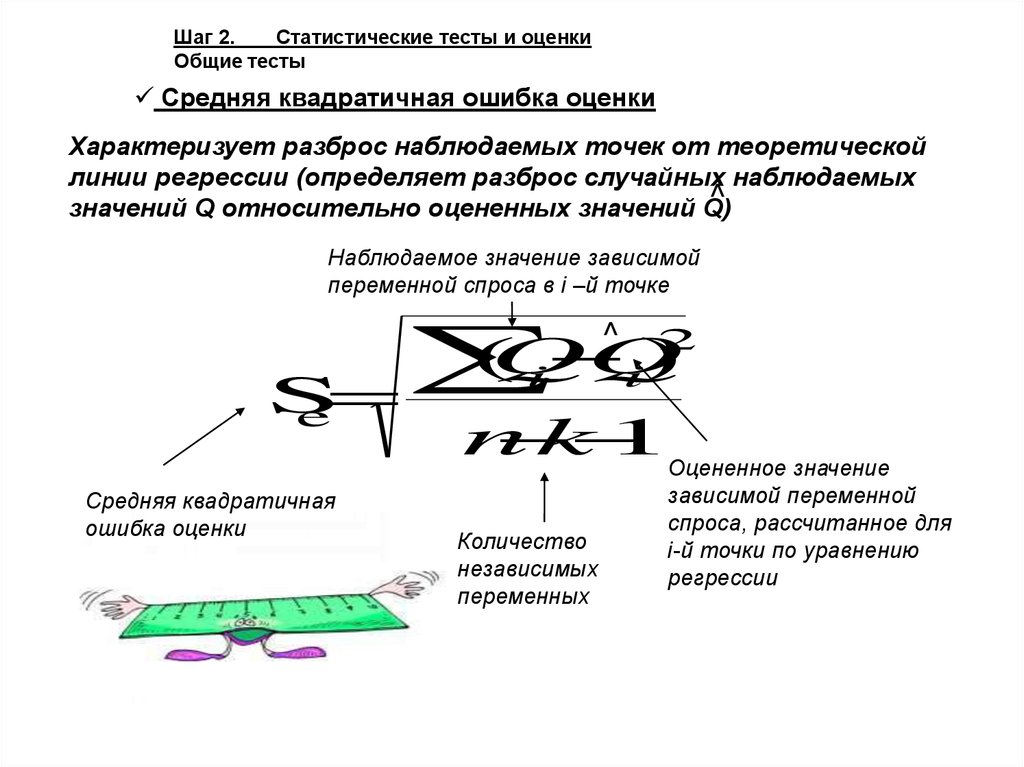
Средняя квадратичная ошибка оценки
Характеризует разброс наблюдаемых точек от теоретической
линии регрессии (определяет разброс случайных наблюдаемых
^
значений Q относительно оцененных значений Q)
Наблюдаемое значение зависимой
переменной спроса в i –й точке
(
Q
Q
)
S
^
i
e
Средняя квадратичная
ошибка оценки
2
i
n
k
1Оцененное значение
Количество
независимых
переменных
зависимой переменной
спроса, рассчитанное для
i-й точки по уравнению
регрессии

14.

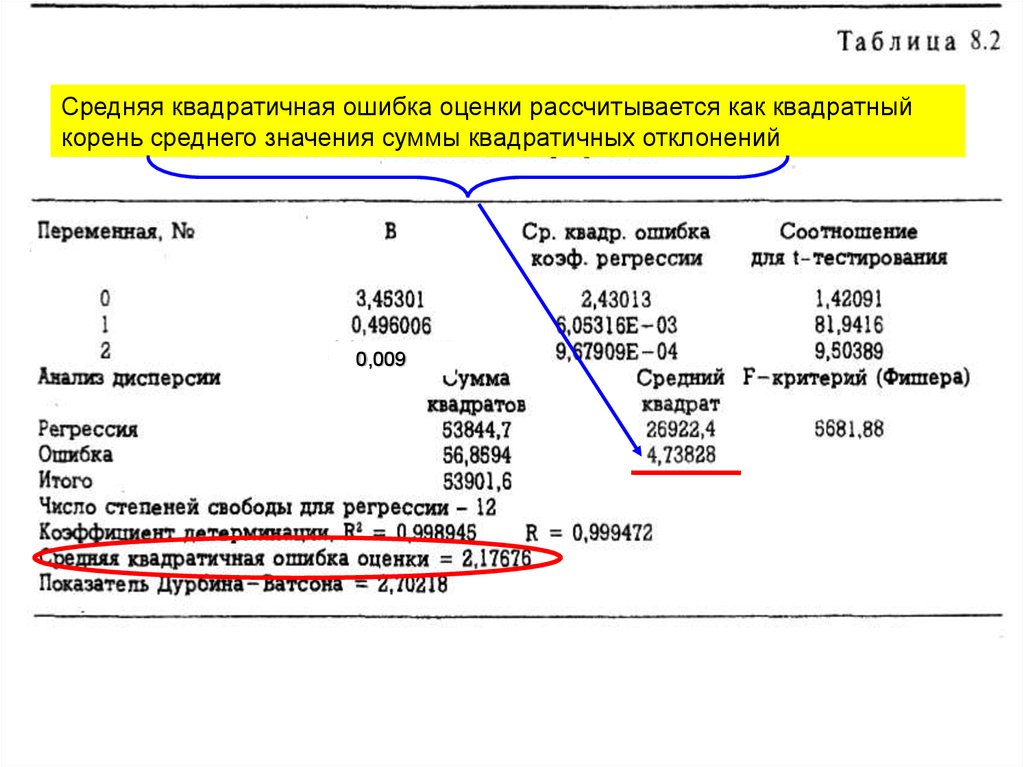
Средняя квадратичная ошибка оценки рассчитывается как квадратный
корень среднего значения суммы квадратичных отклонений
0,009