Погрешности измерений

1. Погрешности измерений

Погрешность измерения - отклонение результата измерения от
истинного значения измеряемой величины. Различают абсолютную
и относительную погрешность измерения.
Абсолютная погрешность измерения равна разности между
результатом измерения А и истинным значением измеряемой
величины Х:
A X
Относительная погрешность измерения
Методическая погрешность.
Внешние погрешности.
Субъективные погрешности.
X
Систематические погрешности.

2. Погрешности измерений

• Инструментальные погрешности:
• Инструментальные погрешности, являющиеся
следствием износа, старения или неисправности
СИ.
• Погрешности, возникающие вследствие
неправильной установки СИ, их неправильным
взаимным расположением, влиянием внешних
воздействий.

3. Погрешности измерений

– Способы исключения и учета систематических
погрешностей.
– Четыре основные группы:
– устранение источников погрешностей до начала
измерений;
– исключение погрешностей в процессе измерения
способами замещения, компенсации погрешности
по знаку, противопоставления, симметричных
наблюдений;
– внесение поправок в результат измерения;
– оценка границ не исключенных систематических
погрешностей.

4. Погрешности измерений

• Устранение источников погрешностей до начала
измерений.
Под устранением источника погрешностей понимается как его
непосредственное удаление (например, удаление источника
тепла), так и защиту СИ и измеряемого объекта от влияния этих
источников. Источники инструментальной погрешности,
присущие конкретному экземпляру СИ, могут быть устранены
путем его калибровки или ремонта. Источники погрешностей,
связанные с неудачным взаимным расположением СИ могут
быть устранены перед началом измерений.

5. Погрешности измерений

• Устранение систематических
погрешностей
• Одним из наиболее распространенных способов
исключения систематических погрешностей является
способ замещения.
• Он заключается в том, что измеряемый объект
заменяется известной мерой, находящейся в тех же
условиях, в какой находился он сам.

6. Погрешности измерений

• Способ компенсации погрешности по
знаку.
• Измерение проводят дважды так, чтобы известная по природе,
но неизвестная по размеру погрешность входила в результаты
измерений с противоположными знаками. Погрешность
исключается при вычислении среднего значения. В
алгебраической форме это можно выразить следующим
образом.
х1 х2 х Д х Д
х
хД .
2
2

7. Погрешности измерений

• Случайные погрешности
Математические модели случайной погрешности.
• Прислучайных погрешностях результат каждого измерения
Аi будет отличаться от истинного значения Х измеряемой
величины:
Ai X X
Эту разность называют случайной погрешностью
отдельного наблюдения.
Истинное значение Х нам неизвестно. Однако проведя
большое количество наблюдений можно определить
среднее значение

8. Погрешности измерений

• Среднее арифметическое ряда
измерений:
n
A1 A2 A3 An
A
n
A
i 1
i
n
Это наиболее вероятный результат измерения

9. Погрешности измерений

• Гауссовский закон распределения
(в практике радиоизмерений наиболее распространён)
1
( X ) 2
p( X )
e
2
2 2
p( X) - плотность вероятности случайной погрешности
n
2
(
A
X
)
i
1
n
n
2
(
X
)
i
1
n
X A i X

10. Погрешности измерений

• Функция Гаусса Графически изображается
колоколообразной кривой, симметричной относительно
ординат, асимптотически приближающейся к оси абсцисс.
Максимум этой кривой получается в точке Х=0, а величина
этого максимума
p ( X ) 1 2

11. Погрешности измерений

• Вероятность появления погрешности в пределах
между Х1 и Х2 определяется площадью
заштрихованного участка на предыдущем рис. т.е.
определённым интегралом от функции p( Х):
x2
1
p( X 1 X X 2 )
e
x1 2
1 X 2
2
d ( X )

12. Погрешности измерений

• Из таблиц, приведенных в математических
справочниках, следует что значение интеграла
P( X ) 0,683;P( 3 X 3 ) 0,9973
• Таким образом с вероятностью 0,683 случайные
погрешности измерения не выходят за пределы ± .
С вероятностью 0,997 случайная погрешность
находится в пределах ± 3 , т.е. только 3 измерения из
1000 могут дать погрешность превышающую ± 3 .
Это соотношение называется законом трёх сигм.

13. Погрешности измерений

• Представленные ф-лы выведены из расчета, что
n
На практике число измерений конечно.
Однако, при увеличении числа измерений
A
и Х сближаются и формула принимает вид;
n
s
U
2
i
1
n 1
n
( A A)
i
1
n 1
2

14. Погрешности измерений

• Средее квадратическое отклонение среднего
арифметического
n
sA
s
n
U
2
i
1
n(n 1)

15. Погрешности измерений

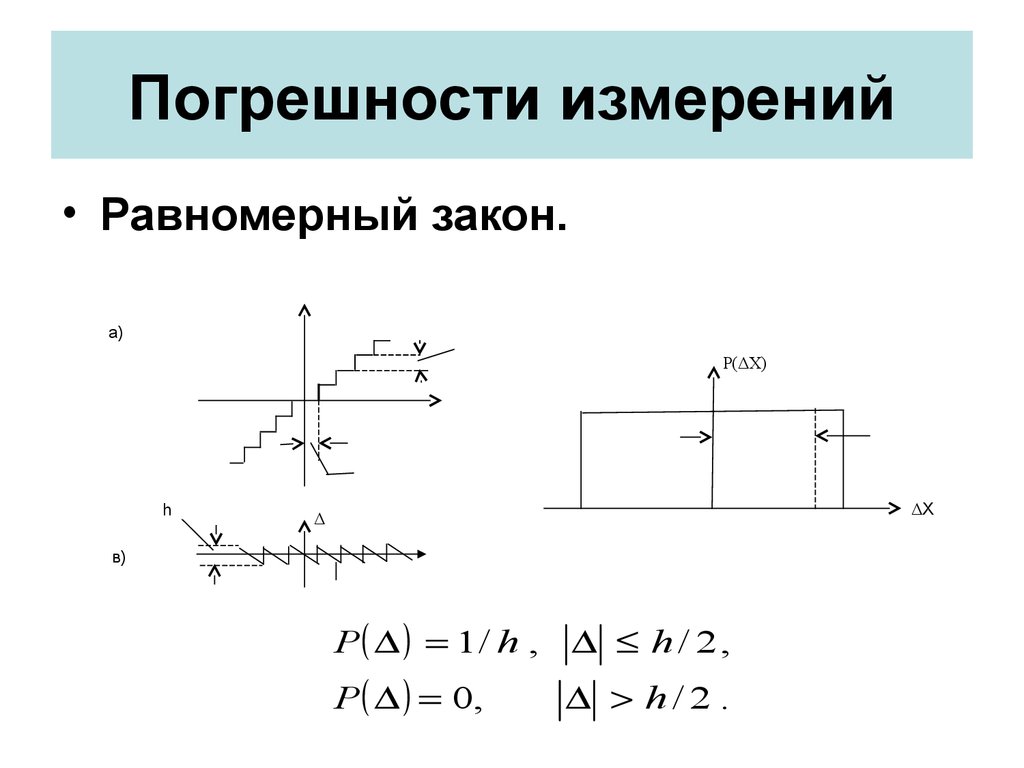
• Равномерный закон.
а)
P(ΔX)
h
ΔX
Δ
в)
P 1/ h , h / 2 ,
P 0,
h/2 .

16. Погрешности измерений

Дисперсия случайной погрешности при равномерном
законе
D
h / 2
2
2
P
d
h
/ 12.
h / 2
Среднее квадратическое отклонение
h
П
D
12
3

17. Погрешности измерений

• Треугольный закон распределения погрешностей.
Треугольный закон является композицией двух равномерных
законов с одинаковой дисперсией.
P(ΔX)
0
1
Х
при П Х 0 ,
2
П
П
Х
1
Р Х 2
при 0 Х П
П П
ΔX
0 при Х П ; Х П .
,

18. Погрешности измерений

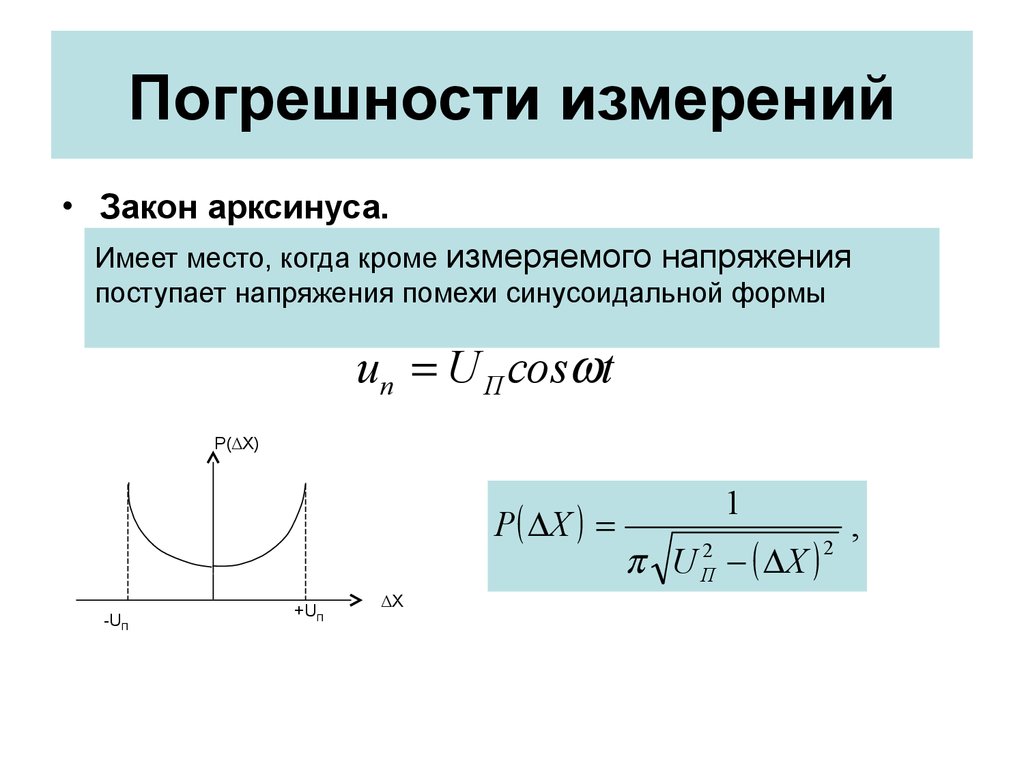
• Закон арксинуса.
Имеет место, когда кроме измеряемого напряженияU Х
поступает напряжения помехи синусоидальной формы
uп U П соs t
Р(ΔХ)
Р Х
-UП
+UП
ΔХ
1
U Х
2
П
2
,