Интервальное оценивание данных

1.

ИНТЕРВАЛЬНОЕ
ОЦЕНИВАНИЕ
ДАННЫХ

2.

Любая величина, оцениваемая по выборке,
может отклоняться от точного значения
Задача:
определить значение величины для
генеральной совокупности
оценить точность, с которой можно
гарантировать результат

3.

Доверительным интервалом называют интервал,
рассчитанный таким образом, что параметр
генеральной совокупности попадает в данный
интервал с заданной вероятностью.
Вероятность того, что параметр совокупности
будет принадлежать доверительному интервалу
называют уровнем доверительности γ.
Величину (1-γ) называют уровнем значимости α.

4. Двусторонний доверительный интервал для среднего

С вероятностью 1- среднее генеральной
совокупности находится в интервале
х t
2
,n 1
S
n
x t
2
,n 1
S
n

5. Односторонний доверительный интервал для среднего

С вероятностью 1- среднее генеральной
совокупности находится в интервале
x t ,n 1
S
n

6. Односторонний доверительный интервал для среднего

С вероятностью 1- среднее генеральной
совокупности находится в интервале
S
х t , n 1
n

7. Условия корректного построения доверительного интервала

1) данные должны представлять собой
случайную выборку из рассматриваемой
генеральной совокупности;
2) данные должны подчиняться нормальному
закону распределения.

8. Доверительный интервал для дисперсии

С вероятностью 1- дисперсия генеральной
совокупности находится в интервале
(n 1) S
2
2
, n 1
2
2
(n 1) S
2
1
2
, n 1
2

9. Доверительный интервал для стандартного отклонения

С вероятностью стандартное отклонение
генеральной совокупности находится в
интервале
S
n 1
2
2
, n 1
S
n 1
2
1 , n 1
2

10. Доверительный интервал для доли признака

С вероятностью доля признака в генеральной
совокупности находится в интервале
pn (1 pn )
pn (1 pn )
pn z
p pn z
n
n
2
2

11.

ПРОВЕРКА
СТАТИСТИЧЕСКИХ
ГИПОТЕЗ

12. Статистическая гипотеза

Н0: утверждение о свойствах генеральной
совокупности
Н1: альтернативное суждение о свойствах
генеральной совокупности

13. Пример

Гипотеза Н0 : среднее значение
параметра равно 32
Альтернатива Н1 : среднее значение
параметра не равно 32

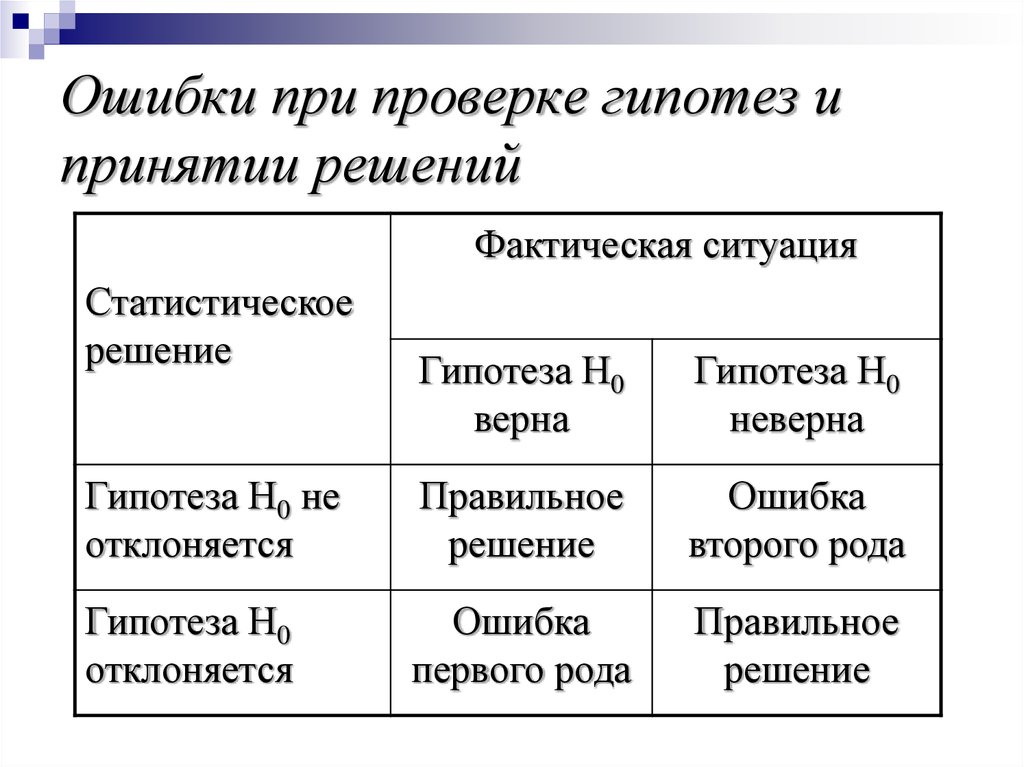
14. Ошибки при проверке гипотез и принятии решений

Фактическая ситуация
Статистическое
решение
Гипотеза Н0
верна
Гипотеза Н0
неверна
Гипотеза Н0 не
отклоняется
Правильное
решение
Ошибка
второго рода
Гипотеза Н0
отклоняется
Ошибка
первого рода
Правильное
решение

15. Общая схема проверки гипотез

1. Формулировка проверяемой (нулевой) и
альтернативной гипотез;
2. Выбор соответствующего уровня значимости α;
3. Выбор критерия K для проверки;
4. Определение критической области и области
принятия гипотезы;
5. Вычисление наблюдаемого значения критерия;
6. Принятие статистического решения.