Міцність при змінних навантаженнях. (Лекція 4)

1. МІЦНІСТЬ ПРИ ЗМІННИХ НАВАНТАЖЕННЯХ

Лекція 4.
проф. Шукаєв С.М.
Національний технічний університет України
“Київський політехнічний інститут”
2012 р.

2. Зміст лекції

ВПЛИВ ЕКСПЛУАТАЦІЙНИХ
ФАКТОРІВ НА ВЕЛИЧИНУ ГРАНИЦІ
ВИТРИВАЛОСТІ
Вплив напруженого стану на границю
витривалості
Вплив неоднорідності напруженого стану
Теорія Серенсена
Теорія Писаренка-Лебедєва
Узагальнений критерій Біргера
Врахування асиметрії циклу при
складному напруженому стані
2012 р.
Лекція №4
2

3. Вплив напруженого стану на границю витривалості

Вплив напруженого стану на границю витривалості
визначається неоднорідністю напруженого стану
і відношеннями головних напружень.
Напружений стан, при якому значення головних
напружень залишаються незмінними по всій
робочій
довжині
зразка,
називають
однорідним
(розтягання-стискання,
чистий
зсув).
Напружений стан, при якому значення головних
напружень змінюється по висоті або іншому
виміру
зразка,
називають
неоднорідним
(згинання, кручення, концентратори напружень).
2012 р.
Лекція №4
3

4. Вплив напруженого стану, продовження

Величиною,
яка
характеризує
степінь
неоднорідності напруженого стану, є градієнт
напружень
d x
G
dx
або відносний градієнт напружень
1 d x G
G
dx
2009 р.
Лекція №3
4

5. Вплив напруженого стану, продовження

Аналіз впливу неоднорідного напруженого стану на
границю витривалості дозволяє зробити наступні
висновки:
границя витривалості підвищується за неоднорідного
напруженого стану у порівнянні із однорідним, що
спостерігається як при лінійному (згин, розтяганнястискання)
так
і
при
плоскому
(кручення)
напруженому стані.
Наприклад, для маловуглецевої сталі з границею міцності
в=400МПа відношення границі витривалості при
чистому крученні отриманому на суцільних і
трубчастих зразках складає:
1 тр
1
2009 р.
Лекція №3
0,808
5

6. Вплив напруженого стану, продовження

збільшення
G
призводить
до
суттєвого
збільшення місцевих напружень, у тому числі й
у концентраторах, які відповідають границі
витривалості;
за умов неоднорідного напруженого стану,
границі витривалості металів і сплавів у
випробуваннях залежать від форми поперечного
перерізу зразка і схеми навантажування.
Границя
витривалості
збільшується
із
зменшенням об’єму металу, який знаходиться у
зоні максимальних напружень. Тобто фактично
проявляється масштабний ефект.
2009 р.
Лекція №3
6

7. Вплив напруженого стану, продовження

Експериментально встановлено:
1
для сталей і алюмінієвих сплавів 0,60
1
для титанових сплавів
1
0,514
1
для чавунів
1
0,80
1
2009 р.
Лекція №3
7

8. Вплив напруженого стану, продовження

Для приблизної оцінки границь витривалості при
розтяганні-стисканні,
згинанні
та
крученні
рекомендуються наступні співвідношення:
р
1
0,85( 1 ) зг Сталь
1 0,55( 1 ) зг Сталь
р
1
0,65( 1 ) зг Чавун
1 0,8( 1 ) зг Чавун
2009 р.
Лекція №3
8

9. Вплив напруженого стану, продовження

Як
в умовах статичного так і циклічного
навантажування критерії граничного стану, як
правило, формуються за допомогою концепції
еквівалентних
параметрів
(напружень,
деформацій, енергії за цикл). В термінах
еквівалентних напружень умова граничного
стану записується наступним чином:
М , 5%
екв f ( 1 , 2 , 3 , mi ) н T , 5%
R
2009 р.
Лекція №3
9

10. Вплив виду напруженого стану, продовження

Третя і четверта теорії міцності записуються так
IV
екв
2
2
III
екв
1a 3a 1
1a 2a 2a 3a 1a 3a
2
2
2
1
В умовах плоского напруженого стану ці теорії
виглядають так
III
2
2
екв a 4 a 1
IV
екв
a2 3 a2 1
2009 р.
Лекція №3
10

11. Вплив виду напруженого стану, продовження

За третьою теорією міцності
За четвертою теорією міцності
21
4
2
1
21
3
2
1
a2 a2
2 1
2
1 1
Рівняння Геста-Мора
a
1
2
2
1 a 1 a
2
1
1
1 1
1
1
Дані рівняння є справедливими для
випадку синхронної та синфазної зміни
компонент тензора напружень.
2009 р.
Лекція №3
11

12. Вплив напруженого стану, продовження

Дослідження в області фізики твердого тіла демонструють,
що реалізувати процес руйнування тіла тільки від
нормальних або тільки від дотичних напружень
практично неможливо.
Досягнення граничного стану обумовлено здатністю
матеріалу здійснювати опір як дотичним так і
нормальним напруженням.
До теорій, які одночасно враховують механізми руйнування
як за дотичними, так і нормальними напруженнями,
відносяться:
теорія Геста-Мора,
теорія Серенсена,
теорія Писаренка-Лебедєва.
2009 р.
Лекція №3
12

13. Теорія Серенсена

Серенсен вважав, що “умовою міцності, яка достатньо
повно охоплює втомні властивості конструкційних
металів, є гіпотеза октаедричних дотичних напружень,
яка крім того враховує ще і вплив нормальних
октаедричних напружень на міцність ”.
окт a K окт a окт 1
окт a
1
2
K 6
1
- амплітуда дотичних напружень, що діють на
октаедричній площадці;
окт a - амплітуда нормальних напружень, що діють на
октаедричній площадці.
2009 р.
Лекція №3
13

14. Теорія Писаренка-Лебедєва

Г.С. Писаренко та А.О. Лебедєв (ІПМ НАН
України) запропонували шукати критерії
міцності
у
вигляді
інваріантних
по
відношенню до напруженого стану функцій
дотичного і максимального напруження.
Лінійній варіант критерію записується так
окт т1 1 т2
де m1 та m2 - константи матеріалу; окт - дотичне
напруження, що діє на октаедричній площадці; σ1 –
максимальне напруження.
2007 р.
Лекція №4
14

15. Теорія Писаренка-Лебедєва, продовження

При узагальненні критерію Писаренка-Лебедєва
на випадок втомного
руйнування можна
одержати наступну залежність
і ,а (1 ) 1,а 1
1
1
3 1 1
1
де σ-1 і -1 - границя витривалості при розтяганністиканні і знакозмінному крученні, відповідно.
2007 р.
Лекція №4
15

16. Узагальнений критерій Біргера

Біргер запропонував узагальнений критерій, який
включає в себе багато відомих критеріїв як
часткові випадки.
Критерій має такий вигляд:
екв ,а 0 і ,а 1 1,а 2 2,а 3 3,а 1
У загальному випадку критерій є
чотирьохпараметричним, тому що для
визначення параметрів 0 , 1 , 2, , 3
необхідно провести чотири базові досліди при
різних видах напруженого стану.
2007 р.
Лекція №4
16

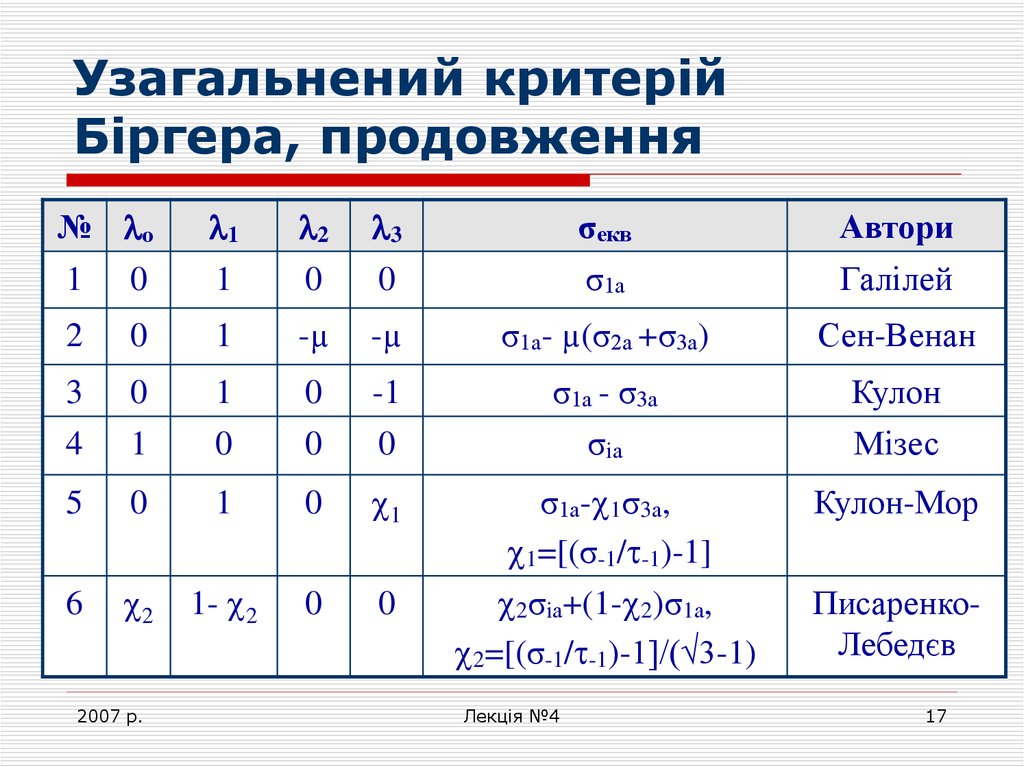
17. Узагальнений критерій Біргера, продовження

№ о
1 0
1
1
2
0
3
0
σекв
Автори
σ1а
Галілей
2
0
1
-µ
-µ
σ1а- µ(σ2а +σ3а)
Сен-Венан
3
0
1
0
-1
σ1а - σ3а
Кулон
4
1
0
0
0
σiа
Мізес
5
0
1
0
1
σ1а- 1σ3а,
1=[(σ-1/ -1)-1]
Кулон-Мор
6
2
1- 2
0
0
2σiа+(1- 2)σ1а,
2=[(σ-1/ -1)-1]/(√3-1)
ПисаренкоЛебедєв
2007 р.
Лекція №4
17

18.

ДЯКУЮ ЗА УВАГУ!
2007 р.
Лекція №4
18