Аппаратные способы реализации ШИМ

1. 1.5. РАСЧЕТ КОДА МОДУЛЯЦИИ

Новосибирский Государственный Технический Университет
Факультет Радиотехники, Электроники и Физики
И. А. Баховцев
1.5.1. Аппаратные способы реализации
ШИМ
Компараторный
Таймерный
(спец. ШИМ-модуль)
(МК общего назначения)
1.5.состояние
РАСЧЕТ
КОДА
МОДУЛЯЦИИ
• Текущее
двоич• В регистр
периода таймера
ного счетчика (аналог ГОН)
заносится цифровой код длисравнивается в цифровом
тельности, двоичный счетчик
компараторе с кодом модузапускается в режиме вычиталирующего сигнала, храния. По обнулению счетчика
нящимся в регистре сравтаймер формирует запрос на
нения (аналог ГМН). На
прерывание для формирования
выходе компаратора форсигналов ШИМ.
мируются сигналы ШИМ.
• Сервисные функции управле• Автоматическая реализания АИН реализуются другими
ция сервисных функций
периферийными устройствами
управления АИН.
или внешними схемами.

2. 1.5.2. Синусоидальная ШИМ, биполярный опорный сигнал

Задача: вывести выражение для ц
синусоидального модулирующего
модуляции) при изменении его
Синусоидальная
ШИМ,
заданной ступенчатой аппроксимации
1.5.2.
биполярный опорный сигнал

3.

Расчет кода модуляции – это вопрос развертывания модулирующего сигнала по амплитуде.
(К - относительное дискретное время)
Исходные положения:
1. Уравнение фазовой модуляции - eм (t ) eоп (t ) ,
его решение - положение фронтов прямоугольных
импульсов на периоде Топ.
2. Модулирующий и опорный сигналы – идеальные
биполярные сигналы.
3. В линейном диапазоне регулировочной характеристики изменение модулирующего сигнала по
амплитуде происходит в области существования
опорного сигнала.
Замечание. Если уравнение F1(x) = F2(x) имеет решение х=Q, то
уравнение F1(x) + C = F2(x) + C (где С – константа) имеет то же
самое решение.

4.

Пусть Еоп=1, тогда Ем=М.
Выражение для модулирующего сигнала:
М[К]=МS[К]
Цифровой аналог ГОН – двоичный счетчик, цифровой
выход которого – положительное число.
2
1
t
Это - первая смещенная функция F1(x) + C
M '[ K ] 1 MS[ K ]
Это вторая смещенная
функция: F2(x)+C
•При единичной глубине модуляции и изменении ступенчатой синусоидальной функции S[K] в диапазоне от 1
до +1 величина M’[K] будет меняться в диапазоне от 0 до 2.

5.

Синусоидальная ШИМ, биполярный
опорный сигнал
Состояние двоичного счетчика меняется от нуля
до некоторой программируемой величины,
которая называется кодом периода (Nmax).
При цифровой реализации ШИМ эта величина равна
размаху опорного сигнала, т.е. двум. Тогда в системе координат двоичного счетчика 1 N max / 2 .
Умножим на «единицу» вторую смещенную функцию
и окончательно получим:
Nmax
Nm[ K ]
1 MS[ K ]
2

6.

Код периода опорного сигнала
определяется из выражения:
Tоп N maxTт K тш
где ТТ период импульсов, тактирующих двоичный
счетчик;
KTШ – коэффициент, зависящий от типа ШИМ.
Для ОШИМ KTШ =1.
Для ДШИМ KTШ =2.

7.

Пример расчета кода модуляции.
Дано:
Nm[k] для фазы A для фазы B для фазы C
K
S[K]
10-йK код
16-й
код 16-й код
16-й код
• Nст = 12, т.е.
0,( N
ст 1) 0,11
161
A1
04
DA
•0
Nmax0,259
= 255
218
DA
04
A1
•1
М =0,707
1,0
•2
модулирующий
сигнал трехфазный
0,966
252
FC
25
5F
3 0,966
252
FC
5F
25
4 0,707
218
DA
A1
04
Nmax
Nm[ K ] A1 1 MS[ K ] DA
5 0,259
161
04
2
6 -0,259
95
5F
FC
25
7 -0,707
37
25
FC
5F
8 -0,966
04
04
DA
A1
9 -0,966
04
04
A1
DA
10 -0,707
37
25
5F
FC
11 -0,259
95
5F
25
FC

8.

Пример расчета кода модуляции.
Математически сдвиг фазы В относительно фазы А
выражается В = 1200.
Замечание. Угол сдвига между фазами
модулирующего сигнала очень важен, особенно при
управлении двигателем. При неправильной фазировке
последний будет вращаться в противоположную
сторону со всеми вытекающими последствиями.

9.

Работа с таблицами кода модуляции.
Процедура извлечения данных из таблиц может быть
выполнена двумя основными способами:
•«один счетчик – три таблицы»
•«три счетчика – одна таблица»
(Здесь «счетчик» – это счетчик номеров ступенек,
который со временем должен инкрементироваться)
Способы извлечения основаны на следующем:
1) Число ступенек в фазах модулирующего сигнала
одинаково и кратно трем, следовательно, взаимное
расположение ступенек всех трех фаз по времени будет
совпадать.
2) Фазы модулирующего сигнала с точностью до угла
сдвига подобны друг другу.

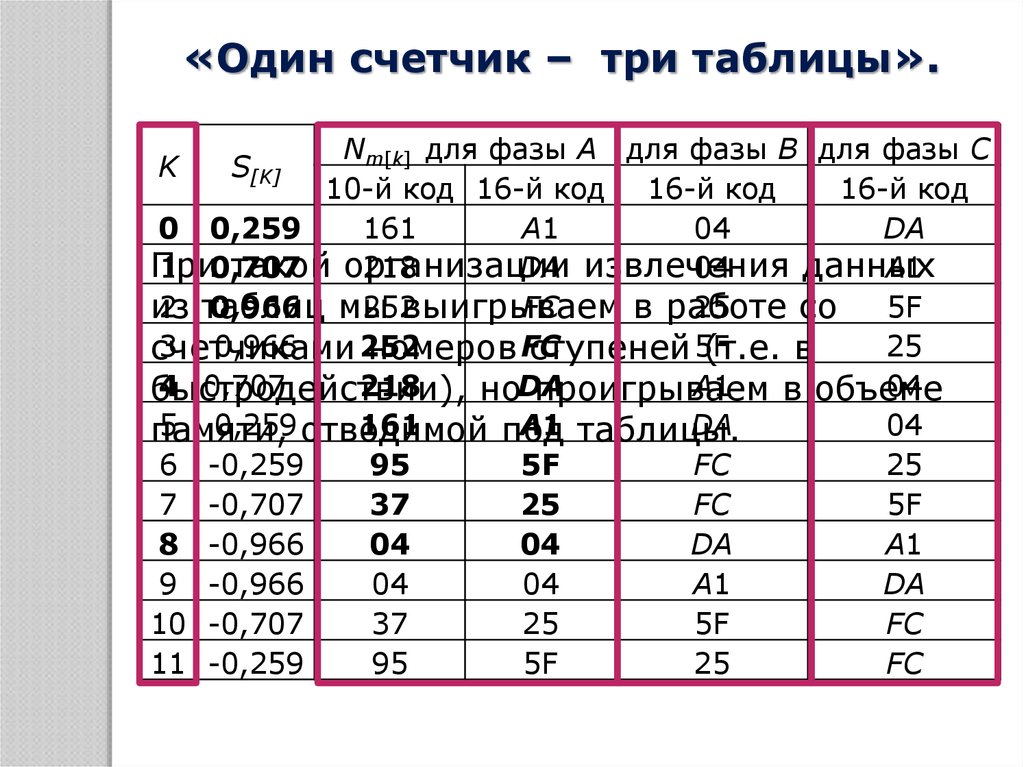
10.

«Один счетчик – три таблицы».
Nm[k] для фазы A для фазы B для фазы C
10-й код 16-й код 16-й код
16-й код
0 0,259
161
A1
04
DA
При
такой организации
данных
1 0,707
218
DA извлечения
04
A1
2 таблиц
0,966 мы
252
FC
25
из
выигрываем
в работе
со 5F
3 0,966
252
25
счетчиками
номеров FC
ступеней 5F
(т.е. в
4 0,707
218
A1
04
быстродействии),
ноDA
проигрываем
в объеме
5 0,259 отводимой
161
A1 таблицы.
DA
04
памяти,
под
6 -0,259
95
5F
FC
25
7 -0,707
37
25
FC
5F
8 -0,966
04
04
DA
A1
9 -0,966
04
04
A1
DA
10 -0,707
37
25
5F
FC
11 -0,259
95
5F
25
FC
K
S[K]

11.

"Три счетчика – одна таблица".
Используем симметрию МС по фазам
Достоинства и недостатки противоположны
предыдущему варианту.
KA 0 1 2 3 4 5 6 7 8 9 10 11
KB 8 9 10 11 0 1 2 3 4 5 6 7
KC 4 5 6 7 8 9 10 11 0 1 2 3
Способ актуален только при большом
количестве ступенек на периоде
модулирующего сигнала (100 и более)
Запомним! Любое уменьшение массивов при
использовании соответствующей симметрии приводит
к усложнению соответствующей программы и
наоборот.

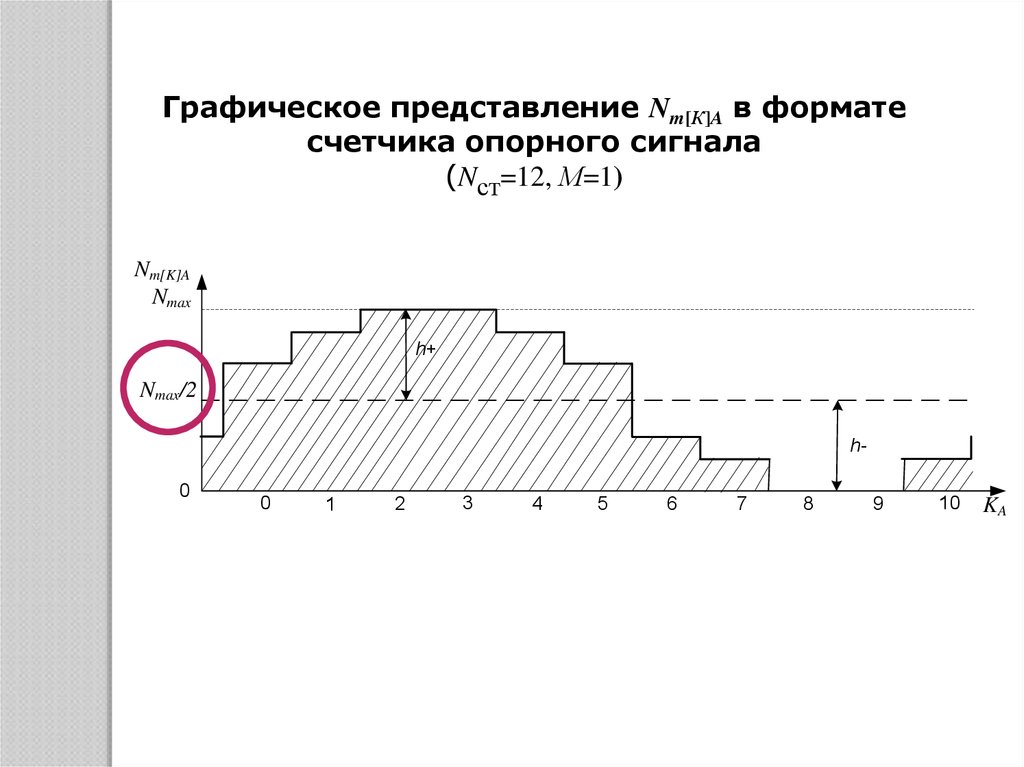
12.

Графическое представление Nm[К]A в формате
счетчика опорного сигнала
(Nст=12, М=1)
Nm[K]A
Nmax
h+
Nmax/2
h0
0
1
2
3
4
5
6
7
8
9
10
KA

13.

Расчет
кода
модуляции
для
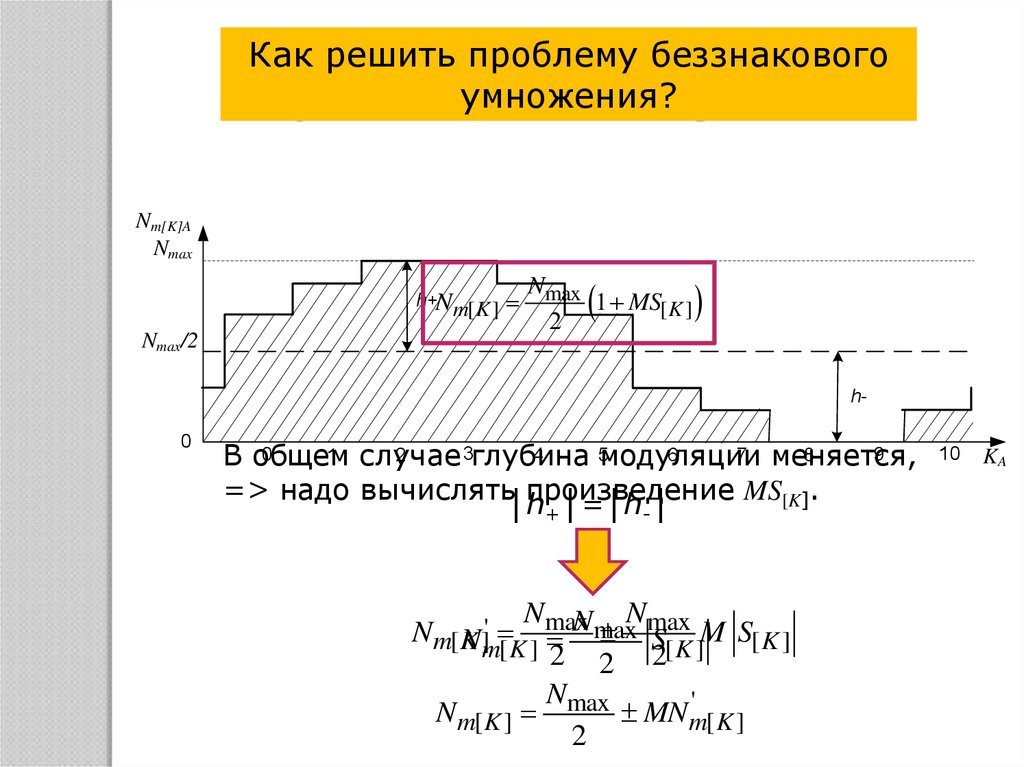
Как решить
проблему
беззнакового
умножения?
отрицательной
полуволны.
Nm[K]A
Nmax
h+N
m[ K ]
Nmax/2
Nmax
1 MS[ K ]
2
h-
0
3глубина
0
9
2
4
5модуляции
6
7 меняется,
8
1 случае
В общем
=> надо вычислять произведение MS[K].
│h+│=│h-│
Nmax
Nmax
Nmax
S[ K ]M S[ K ]
m[ K ]
2 2 2
N
'
Nm[ K ] max MNm
[K ]
2
'
Nm[ N
K]
10
KA

14.

Алгоритм расчета кода модуляции
для варианта «три счетчика – одна таблица»:
1. Выбрать
текущее значение
кода глубины
6.
Инкрементировать
счетчик ступенек
фазы А,
проверить
значение
KA на равенство
модуляции новое
и состояние
счетчиков
номеров Nст:
ступеней
, KKBA, =0.
KC .
если
«да»,KAто
2. П.п.
Для K
из таблицы
значениефаз.
N’m[K].
7.
2A–извлечь
6 выполнить
для остальных
3. Умножить код глубины модуляции на табличное
значение.
4.
Определить полярность
текущей ступеньки
фазы А.
Замечание.
При инициализации
этой процедуры
исходное состояние счетчиков ступеней должно быть
5. Вычислить и сохранить значение кода модуляции
установлено следующим: KA=0, KB=2Nст/3, KC=Nст/3
для фазы А:
Nст
0 KA
1 ,
если
2
Nmax
'
Nm[ K ]
MNm[ K ]
то
используется со знаком
2
«+», иначе со знаком « ».

15.

Алгоритм расчета кода модуляции
для варианта «один счетчик – три таблицы»:
NCT
0 KA
1
В этом случае условие
справедливо
2
только для фазы А. Для фаз В и С условия
определения полярности выглядят иначе.
Фаза В:
NCT
5 NCT
KB
1 , то «+», иначе « ».
если
3
6
Фаза С: N
2 NCT
CT
KС
1 , то « », иначе «+».
если
6
3

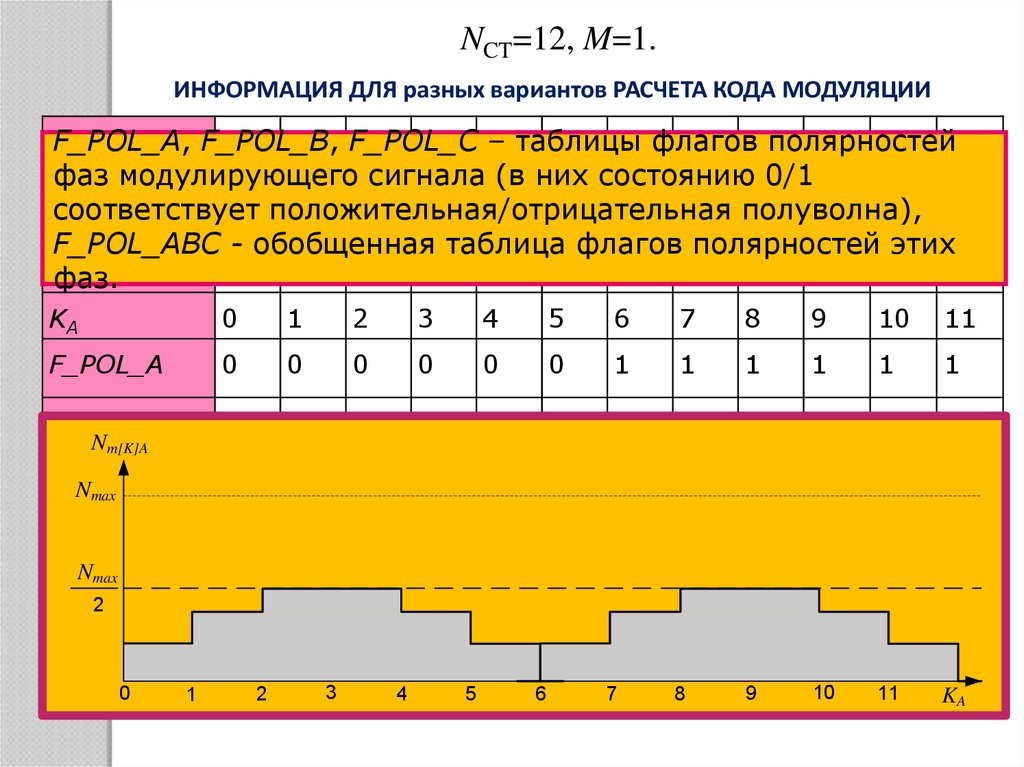
16.

NCT=12, M=1.
ИНФОРМАЦИЯ ДЛЯ разных вариантов РАСЧЕТА КОДА МОДУЛЯЦИИ
F_POL_A,
F_POL_B,
– таблицы
полярностей
N’
$21 $5A F_POL_C
$7C $7C $5A
$21 $21флагов
$5A $7C
$7C $5A $21
m[k] A
фаз модулирующего сигнала (в них состоянию 0/1
N’
$7Cположительная/отрицательная
$7C $5A $21 $21 $5A $7C $7C полуволна),
$5A $21 $21 $5A
m[k] B
соответствует
F_POL_ABC - обобщенная таблица флагов полярностей этих
N’m[k] C
$5A $21 $21 $5A $7C $7C $5A $21 $21 $5A $7C $7C
фаз.
KA
0
1
2
3
4
5
6
7
8
9
10
11
F_POL_A
0
0
0
0
0
0
1
1
1
1
1
1
KB
8
9
10
11
0
1
2
3
4
5
6
7
F_POL_B
1
1
1
1
0
0
0
0
0
0
1
1
KC
4
5
6
7
8
9
10
11
0
1
2
3
Nmax
F_POL_C
0
0
1
1
1
1
1
1
0
0
0
0
02
06
06
04
04
05
05
01
01
03
03
8
9
10
11
KA
Nm[K]A
Nmax
2
F_POL_ABC 02
0
1
2
3
4
5
6
7

17.

1.5.3. Синусоидальная ШИМ,
однополярный опорный сигнал
eоп (t)
eM (t)
t
UУС
yA = UУС
yB = UУС
yA = UA
yA = UB
t
yB = 0
yB = 1
t
yA = UУС
}
}
Несимметричное
управление
}
}
yA = положительной
0
Для
кода модуляции для
yA =расчета
UA
t
Квазисимметполуволны справедливо выражение:
ричное
yB = UУС
yB = N
0
yA = UB
m[ K ] N max MS[ K ] MN 'm[ Kt ] управление
где UKН 0,( Nст / 2 1)
t

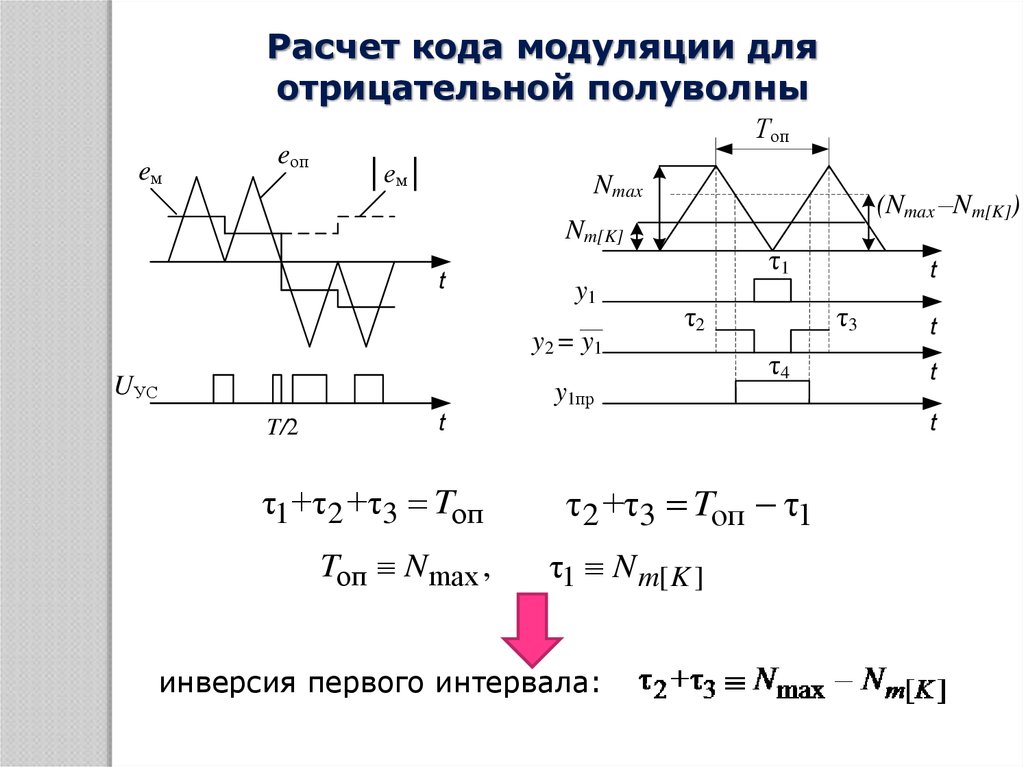
18.

Расчет кода модуляции для
отрицательной полуволны
eм
eоп
Топ
│eм│
Nmax
(Nmax –Nm[K])
Nm[K]
t
y1
y2 = y1
UУС
τ1
τ2
y1пр
T/2
τ3
τ4
t
τ1 +τ 2 +τ3 Tоп
Tоп N max ,
t
t
t
t
τ 2 +τ3 Tоп τ1
τ1 N m[ K ]
инверсия первого интервала:

19.

Программная инверсия – на периоде Топ получаем не два
импульса, а один. 4
τ 2 τ3 , значит y1пр
и
y2
равны по
длительности на периоде опорного сигнала.
Так как площади импульсов не
изменились, то не изменится
первая гармоника и не
появится постоянная
составляющая

20.

Расчет кода модуляции для отрицательной полуволны
Код модуляции для отрицательной полуволны при
однополярном опорном сигнале:
N m[ K ] N max MN 'm[ K ]
K Nст / 2, Nст 1
Nmax
Nm[6]
Nm[4]
Nm[5]
Nm[7]
yА
Алгоритм расчета подобен расчету при биполярном
yВ
ОС: если «+»,то производится суммирование с
константой, если «–», то производится вычитание
UН
из константы.
T/2
T
При биполярном опорном сигнале эта константа
равна Nmax/2, а при однополярном ОС это: при «+»
нуль, а при «–» это Nmax.
t
t
t
t

21.

1.5.4. Расчет кода модуляции для способов
ШИМ со сложной формой модулирующего
сигнала
Синусоидальная ШИМ с
добавлением третьей гармоники.
• для модулирующего сигнала:
eм1
eм
eм eм1 eм2 M sin t L sin3 t
где коэффициент
eм2
L 1/ 6 0,167
υ
Необходимо увеличить
Nст минимум в 2-3 раза
• при ступенчатой аппроксимации:
где K 0,( N ст 1)
S[ K ] sin
NCT
2 K 1 L sin
3
2 K 1
NCT

22.

Расчет кода модуляции для способов ШИМ
Циклическая ШИМ
со сложной формой модулирующего
eм3
сигнала
eм2
eм1
u
0
π/2
2π/3
π
0
Фаза A пассивная
u
Особенности:
•на
полуволне
модулирующего
сигнала
опорного
•число
коммутаций
в АИН на одну
треть форма
меньше
(как и у
сигнала
однополярная;
векторной
ШИМ);
•центральная
сигнала при
•расширенныйчасть
на 15модулирующего
% линейный диапазон
регулировании
не меняется;
регулировочнойамплитуды
характеристик
(как и у векторной
ШИМ).

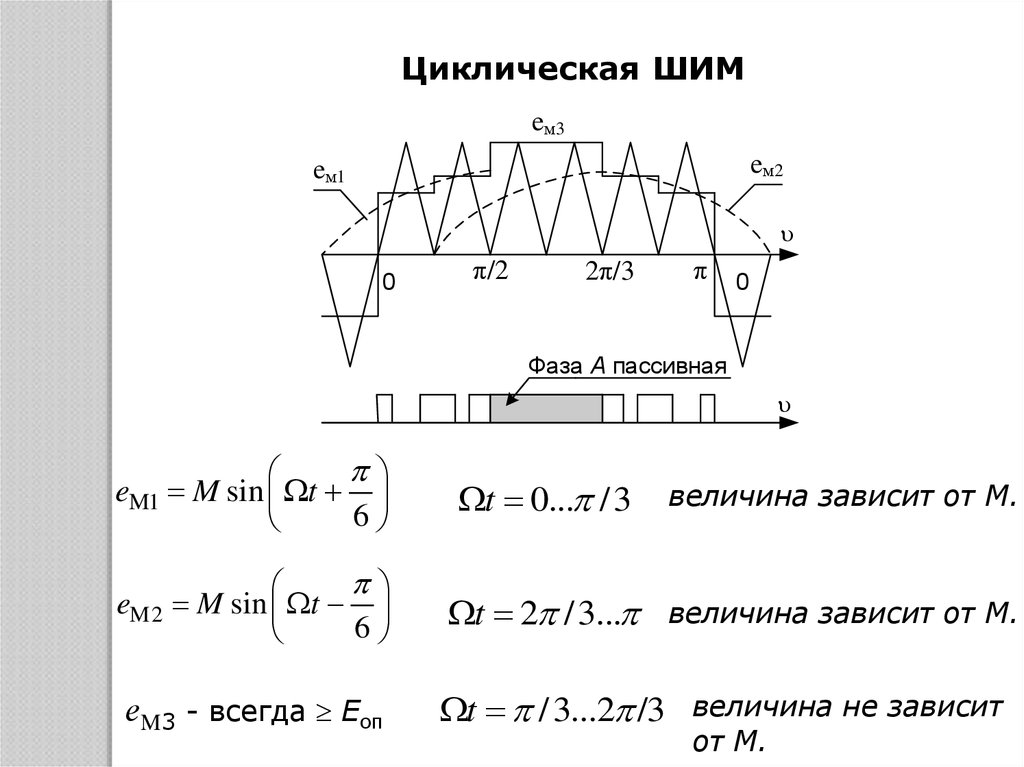
23.

Циклическая ШИМ
eм3
eм2
eм1
u
0
π/2
2π/3
π
0
Фаза A пассивная
u
eM1 M sin t
6
t 0... / 3
величина зависит от M.
eM2 M sin t
6
t 2 /3... величина зависит от M.
еM3 - всегда Еоп
t / 3...2 /3 величина не зависит
от M.

24.

Циклическая ШИМ
S[ K ] sin
2 K 1 , где K 0,( NCT / 6 1)
6 N CT
'
Nm
[ K ] N max S[ K ]
№
0
1
2
3
4
5
6
7
8
9
10
11
N’m[K]
N’m[0]
N’m[1]
H
H
N’m[1]
N’m[0]
N’m[0]
N’m[1]
H
H
N’m[1]
N’m[0]
'
N m[ K ] MNm
[K ]
K 0, NCT / 2 1
'
N m[ K ] N max MN m
[K ]
K NCT / 2, NCT 1

25.

1.5.5. Расчет кода модуляции для
векторной ШИМ
Основы представления векторной ШИМ.
+
+E/2
1
y1
y3
2
y2
UC0
4
y4
5
y5
UB0
UA0
-E/2
3
6
y6
UA
N
ZA
UB
Общая точка нагрузки
ZB
UC
ZC

26.

Основы представления векторной
ШИМ.
Векторы состояния: 000 V0 и 111 V7 – обеспечивают нулевые напряжения в нагрузке («нулевые» векторы), а V1 V6 обеспечивают ненулевые
напряжения («образующие» векторы).
V3
V2
S2
V4
O
S4
S5
d j T j /1
Ts
Вектор
Vi Si
T0
T7
T1Состояния
T2
V
*
V
V
V
V7
2
0
0 0 T 1 04
V
1
Ts
Ts
s 0 -T7.
s
,где j =
S1
V*
S2
V1
0 где
1 Т
01, Т2, Т02
V3
0, Т7 - время
S3
0 существования
1 1
03 одноименных
V4 S6
S6
векторов.
V * d1V01 d02V21 d0V001 d7V7V5 S4
S5
1
0
1
05
V
V6
6
S2
S3
V5
yA yB yC
d1 M sin '
3
1
1
1
0
1
Ts T1 T2 T0 T7
1
07
V
0 0
d0
2 M sin '
06
V2
7
00d d V
1
2 0 d0 d7 1

27.

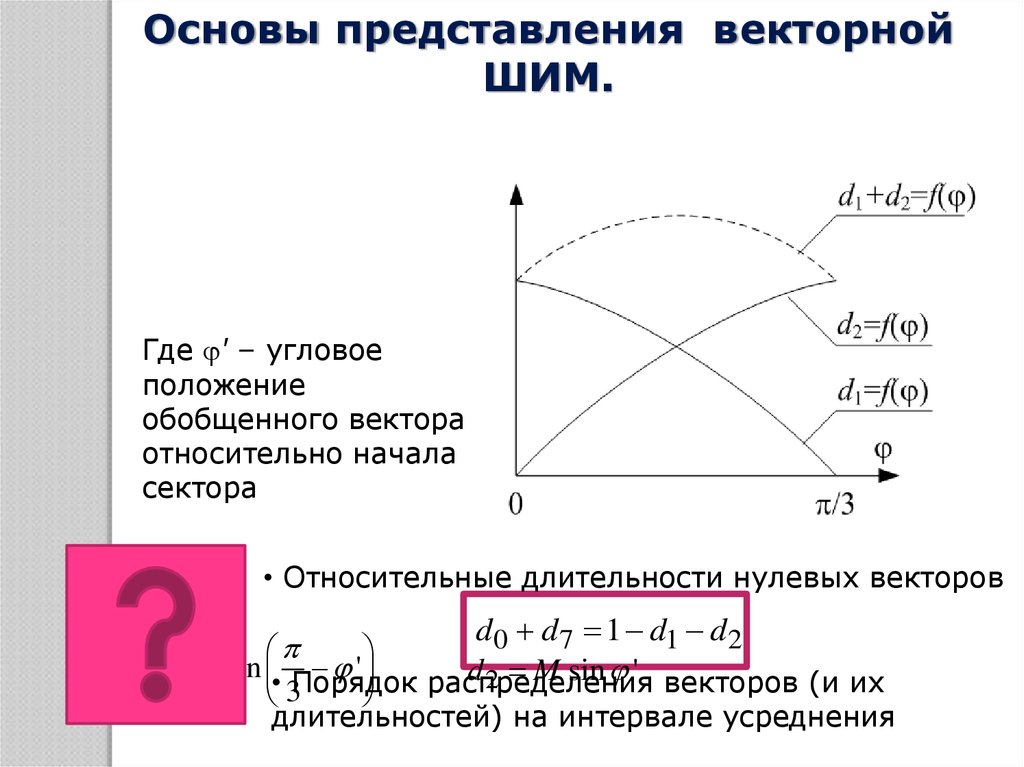
Основы представления векторной
ШИМ.
Где ' – угловое
положение
обобщенного вектора
относительно начала
сектора
• Относительные длительности нулевых векторов
d0 d7 1 d1 d 2
d1 M sin • Порядок
'
d 2 M sin ' векторов (и их
распределения
3
длительностей) на интервале усреднения

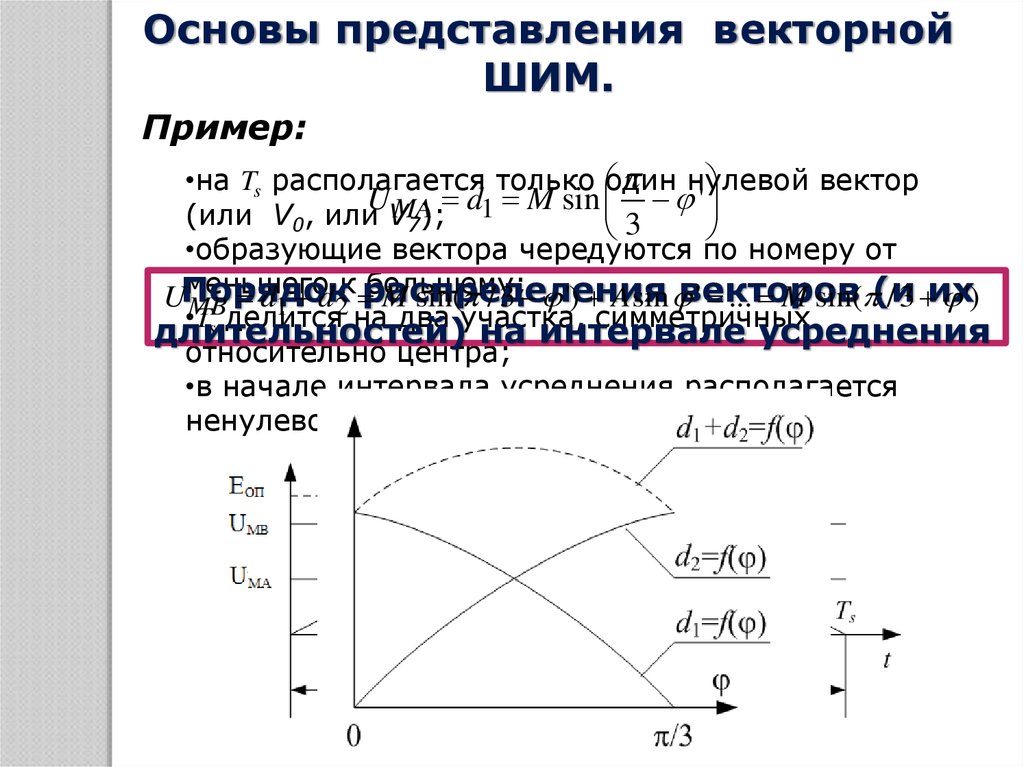
28.

Основы представления векторной
ШИМ.
Пример:
нулевой
•на Ts располагается только один
вектор
U
d
M
sin
'
MA); 1
(или V0, или V
7
3
•образующие вектора чередуются по номеру от
меньшего
к распределения
большему;
UПорядок
d
d
M sin( / 3 ') A sin векторов
' ... M sin( (и
/ 3 их
')
MB
1
2
•Ts делится на два участка, симметричных
длительностей) на интервале усреднения
относительно центра;
•в начале интервала усреднения располагается
ненулевой вектор.

29.

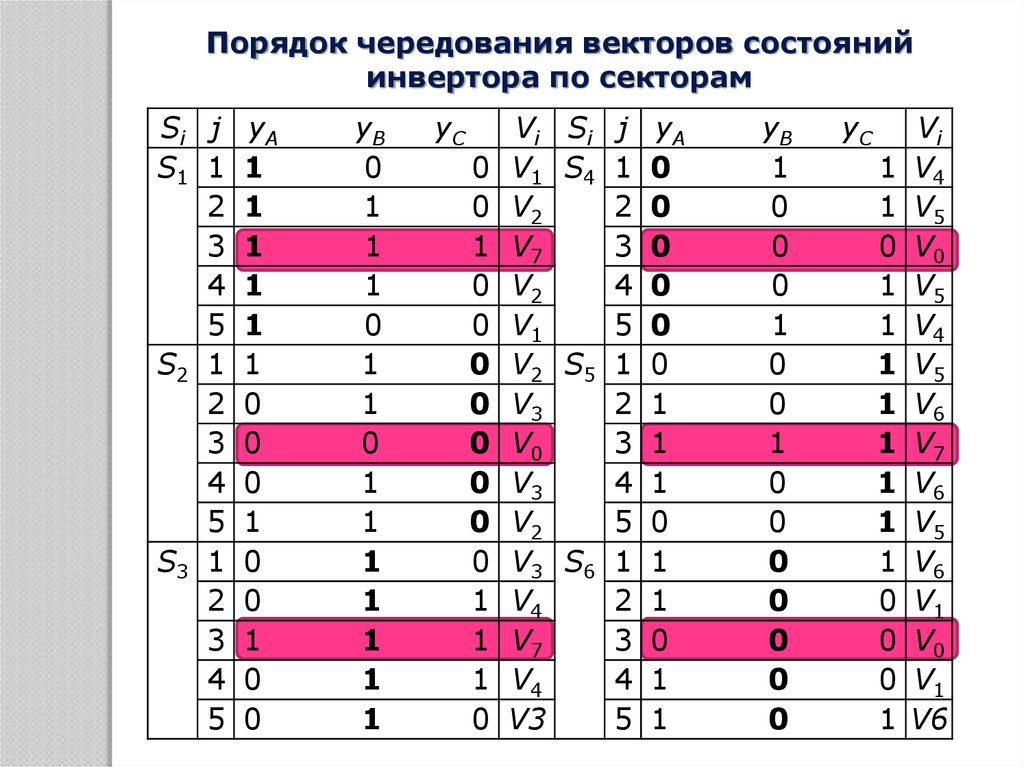
Порядок чередования векторов состояний
инвертора по секторам
Si j yA
S1 1 1
2 1
3 1
4 1
5 1
S2 1 1
2 0
3 0
4 0
5 1
S3 1 0
2 0
3 1
4 0
5 0
yB
0
1
1
1
0
1
1
0
1
1
1
1
1
1
1
yC
0
0
1
0
0
0
0
0
0
0
0
1
1
1
0
Vi
V1
V2
V7
V2
V1
V2
V3
V0
V3
V2
V3
V4
V7
V4
V3
Si j yA
S4 1 0
2 0
3 0
4 0
5 0
S5 1 0
2 1
3 1
4 1
5 0
S6 1 1
2 1
3 0
4 1
5 1
yB
1
0
0
0
1
0
0
1
0
0
0
0
0
0
0
yC
1
1
0
1
1
1
1
1
1
1
1
0
0
0
1
Vi
V4
V5
V0
V5
V4
V5
V6
V7
V6
V5
V6
V1
V0
V1
V6

30.

Микропроцессорная реализация
векторной ШИМ в МК общего назначения
Необходимы:
•таблица
чередования
векторов
состояния
или в
•генератор
треугольного
опорного
напряжения,
таблица необходимо
слов состояния
вентилей
(ССВ);
которой
задать:
Nmax, K
дел, INT1;
•два цифровых
компаратора
модулирующих
сигнала:с возможностью
прерывания по сравнению:
INT СМР1
U MA M sin(
/ 3 , INT
') СМР2;
U
•порты вывода ССВ. MB
M sin( / 3 ')
Задаем Nст, а две
таблицы значений
ступенек рассчитываем
по формулам:
K 0,( Nст / 6 1).
N 'm[ K ] A N max sin
(2 K 1)
3 N CT
N 'm[ K ]B N max sin
(2 K 1)
3
N
CT

31.

Микропроцессорная реализация
векторной ШИМ
Алгоритм реализации в МК:
1. Определяется текущее значение угла ;
2. Вычисляются сектор Sj, угол ', номер ступеньки K;
3. Из таблиц извлекаются N’m[K]A, N’m[K]B, j-я
последовательность слов состояния вентилей
(ССВ1 ССВ5);
4. Вычисляются и сохраняются соответствующие коды
модуляции:
'
N m[ K ] A MN m
[K ]A
'
N m[ K ]B MN m
[ K ]B

32.

В подпрограммах по прерыванию
необходимо выполнить следующие
задачи:
подпрограмма по INT1 в регистры сравнения
компараторов записываются коды Nm[K]A, Nm[K]B, в порт
записывается ССВ1;
подпрограмма по INTCMP1 в порт записывается ССВ2;
подпрограмма по INTCMP2 в порт записывается ССВ3;
подпрограмма по INTCMP2 в порт записывается ССВ4;
подпрограмма по INTCMP1 в порт записывается ССВ5.
Недостаток: 4 (!) дополнительных прерывания на Ts.
Эти недостатки устранены в МК со специализированными ШИМ-модулями (TMS320F2812)

33.

Расчет кода модуляции для
векторной ШИМ
Векторную ШИМ можно представить и во временной
области.
UMB
UMA
u
0
π/3
2π/3
π
Выбор вида представления способа управления
(временного или векторного) при микропроцессорной
реализации зависит от способа регулирования всей
энергетической системы, в которой присутствует АИН.

34.

1.5.6. Умножение на десятичную дробь
1. Замена умножения делением.
MS[ K ]
S[ K ]
1/ M
, где 1/М число больше единицы.
2. Разложение десятичной дроби на степени
числа 2 с отрицательным показателем.
Пример:
0,75 0,5 0,25 2 1 2 2 ,
0,45 0,25 0,125 0,0625 2 2 2 3 2 4
Q0.75 Q0.5 Q0.25 Q 1 Q 2
Разложив
дробь,умножения
получаем алгоритм
обработки когда
Эти способы
используются,
множимого: величина степеней показывает, сколько раз
дробисдвинуть
известны
и программист
заранее
может
нужно
вправо,
а число степеней
- количество
составить алгоритм их реализации.
слагаемых.

35.

Умножение на десятичную дробь
Пример:
Суть:
•восьмиразрядная
шина
данных.
Диапазон изменения
глубины
модуляции
•при
перемножении
произведение
будет
«привязывается»
к байтов
диапазону
чисел 0 …255
(код
двухбайтным
и сохраняется
в двухбайтном
регистре.
глубины модуляции
), выполняется
умножение
,в
3. Использование
особенностей
качестве
результата используется
старший
байт
целочисленного
умножения
двоичных
Представим,
что
от 0 доинкрементом).
255 соответствуют
произведения
(счисла
возможным
чисел.
десятичным дробям от 0 до
1, т.е. 255 ($FF) ~ 1.
Также известно:
•если
некоторое
однобайтное
число Q умножить на $FF, то
Данный
способ
более универсален.
в старшем байте произведения получим (Q 1), т.е. с
Единственным
условием здесь является
точностью до младшего разряда получили умножение
«привязка»
числа Q на 1; единицы глубины модуляции к
максимальному
числу
шины
данных.байте будет
•если число Q умножить
$7F,
то в старшем
(Q/2 1) и т.д.

36.

Умножение на десятичную дробь
4. Универсальный вариант
QM QN M / N M_1
N м_1
- Код, соответствующий единичной
глубине модуляции
Одно действие заменяется двумя:
умножением и делением.
Нужно строго выполнять этот порядок
выполнения операций

37.

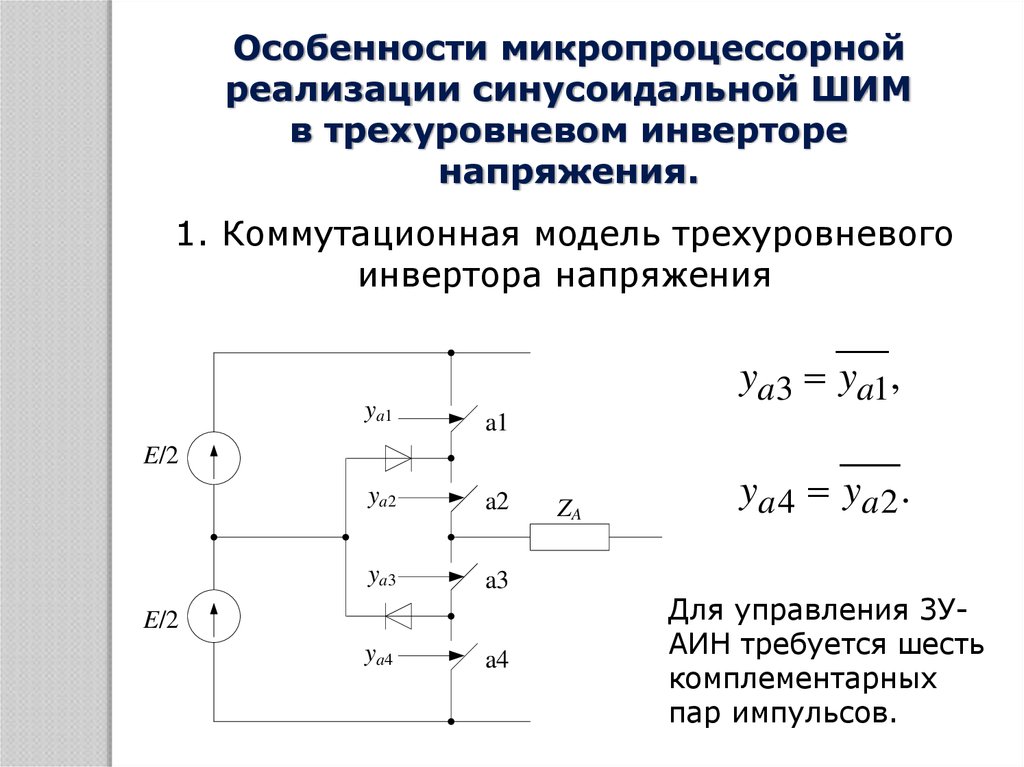
Особенности микропроцессорной
реализации синусоидальной ШИМ
в трехуровневом инверторе
напряжения.
1. Коммутационная модель трехуровневого
инвертора напряжения
ya3 ya1,
ya1
a1
ya2
a2
ya3
a3
E/2
E/2
ya4
a4
ZA
ya 4 ya 2 .
Для управления 3УАИН требуется шесть
комплементарных
пар импульсов.

38.

Особенности микропроцессорной
реализации синусоидальной ШИМ
в трехуровневом
инверторе
e (t)
e (t)
напряжения.
оп1
м
t
T
T/2
eоп2(t)
ya1 = ya3
t
2.
Форма модулирующих и опорных
t
y =y
сигналов
a2
a4
eоп1(t)
eм1(t)
t
eоп2(t)
eм2(t)
t
eоп2(t)
ya1 = ya3
t
t
ya4 = ya2
T/2
T

39.

Необходимые аппаратные средства для ЗУ-АИН
•Наличие двух специализированных ШИМ-модулей «Motion
Control»
•В ШИМ-модулях опорные сигналы должны быть между
собой синхронизированы во времени, но в то же время
противофазны друг к другу
•Один ШИМ-модуль должен работать с положительными
полуволнами, а второй – с модулями отрицательных
полуволн модулирующих сигналов

40.

Спасибо за внимание!