Изотермический процесс в реакционном объеме. (Тема 6.2)

1. Тема 6

Химический процесс на
уровне реакционного
объема

2. Тема 6.2

Изотермический процесс в
реакционном объеме
Режимы
идеального вытеснения и
периодический идеального смешения
Режим проточный идеального
смешения
Сопоставление непрерывных
изотермических процессов в РИВ и
РИС-н

3. Изотермический процесс в реакционном объеме

Отсутствуют тепловые изменения
Происходящие явления
отражаются только в состоянии
материальных потоков

4. РИВ и РИС-п

Математическая модель РИВ и РИС-п
dC
d
W C
при = 0, С = С0
Переходя к конверсии, при = 0, х = 0
C0 dx
d
W C

5. РИВ и РИС-п

Характеристическое уравнение идеального
режима (РИС-п или РИВ)
x
dx
C0
W
C
0

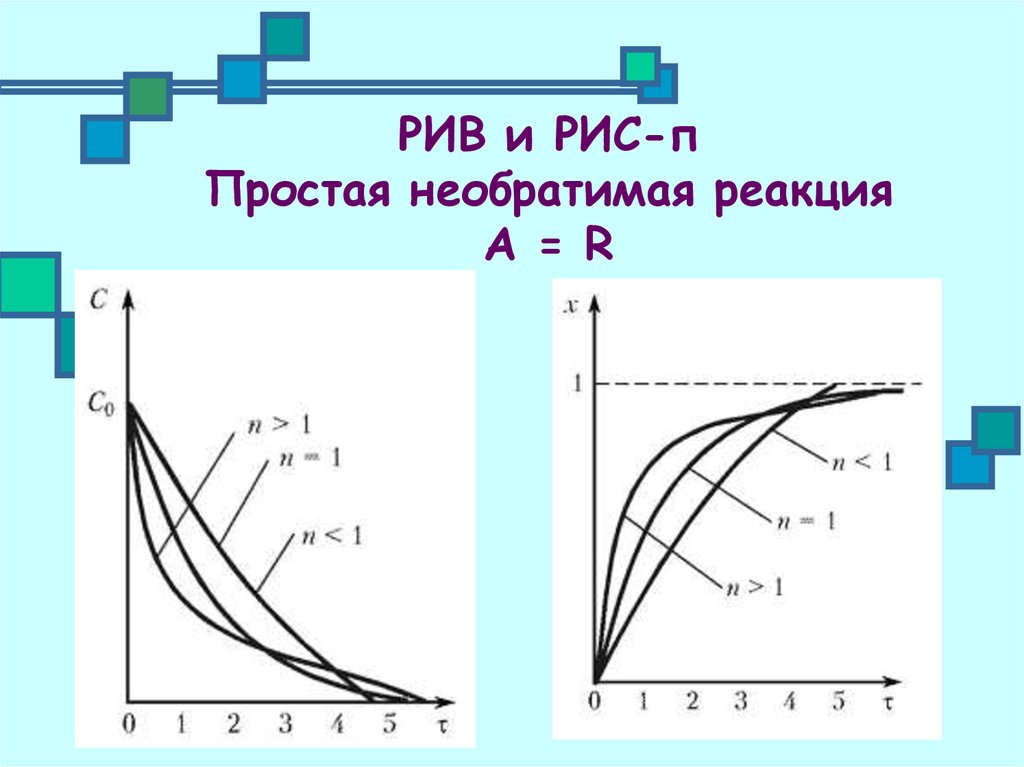
6. РИВ и РИС-п Простая необратимая реакция А = R

Кинетическое уравнение
W(C) = kCn
Модель процесса при = 0, С = С0
dC
d
kC n
при = 0, х = 0
dх
d
kC0n 1 1 x n

7. РИВ и РИС-п Простая необратимая реакция А = R

Интегрируем и получаем
1
1 n
1 n
C
C0 k
n 1
Получаем зависимость С( )
C C01 n 1 n k
1 n
1
и
C
1 n
C0
1
n 1 k n 1
1

8. РИВ и РИС-п Простая необратимая реакция А = R

Вводим конверсию вместо концентрации
1
1 n
n 1
1 1 x
kC0
1 n
Получаем зависимость х( )
1
k 1 n
1 n
x 1
1
C1 n
0
и
x 1
1
1 k n 1 C0n 1 n 1
1

9. РИВ и РИС-п Простая необратимая реакция А = R

10. РИВ и РИС-п Простая необратимая реакция А = R

Влияние
температуры
на
зависимость
С( )
Т2 Т1

11. РИВ и РИС-п Простая необратимая реакция А = R

Влияние С0 на
зависимость х( )
для реакции
порядка n
С02 С01
(сплошные линии –
при С01,
пунктирные – при
С02)

12. РИВ и РИС-п Простая необратимая реакция А = R

Анализ зависимости С( ) и х( ) показывает:
- в РИС-п - влияние условий процесса на
изменение С и х во времени,
- в РИВ – распределение С и х по длине
реакционной зоны.
Эти особенности режимов существенно
сказываются при переносе свойств
моделей на процесс в промышленном
реакторе.

13. РИВ и РИС-п Простая обратимая реакция А = R

Кинетическое уравнение (для реакций 1-го
порядка в обоих направлениях)
W(C) = k1CА – k2CR
Модель процесса при = 0, х = 0 с учетом
СА = С0(1-х) и СR = С0х
dx k 1 x k x
или
1
2
d
dx
d
k1 k1 k 2 x

14. РИС-н Простая обратимая реакция А  R

РИС-н
Простая обратимая реакция
А R
Интегрируем и получаем
ln k1 k1 k 2 x ln k1
k1 k 2
k1
k1 k 2
x
1 e
k1 k 2
или
При →∞ достигается равновесие и конверсия равна
k1
хр
k1 k 2

15. РИВ и РИС-п Простая обратимая реакция А  R

РИВ и РИС-п
Простая обратимая реакция
А R
Анализ
С0: Начальная концентрация реагента не влияет
на степень превращения
Т: k1 и k2 увеличиваются в повышением Т, но k1
увеличивает, а k2 уменьшает скорость.
Суммарный эффект определяется
интенсивностью увеличения k1 и k2, зависящей
от Е1 и Е2. При повышении Т более интенсивно
растет k реакции с большей Е.

16. РИВ и РИС-п Простая обратимая реакция А  R

РИВ и РИС-п
Простая обратимая реакция
А R
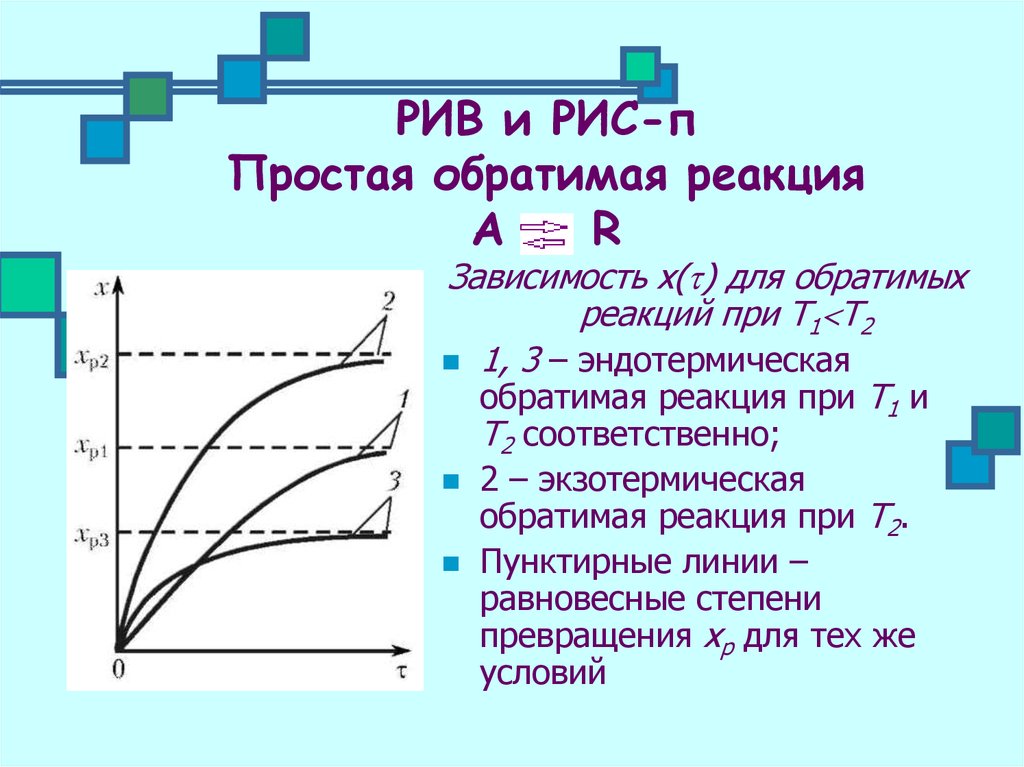
Зависимость х( ) для обратимых
реакций при Т1 Т2
1, 3 – эндотермическая
обратимая реакция при Т1 и
Т2 соответственно;
2 – экзотермическая
обратимая реакция при Т2.
Пунктирные линии –
равновесные степени
превращения хр для тех же
условий

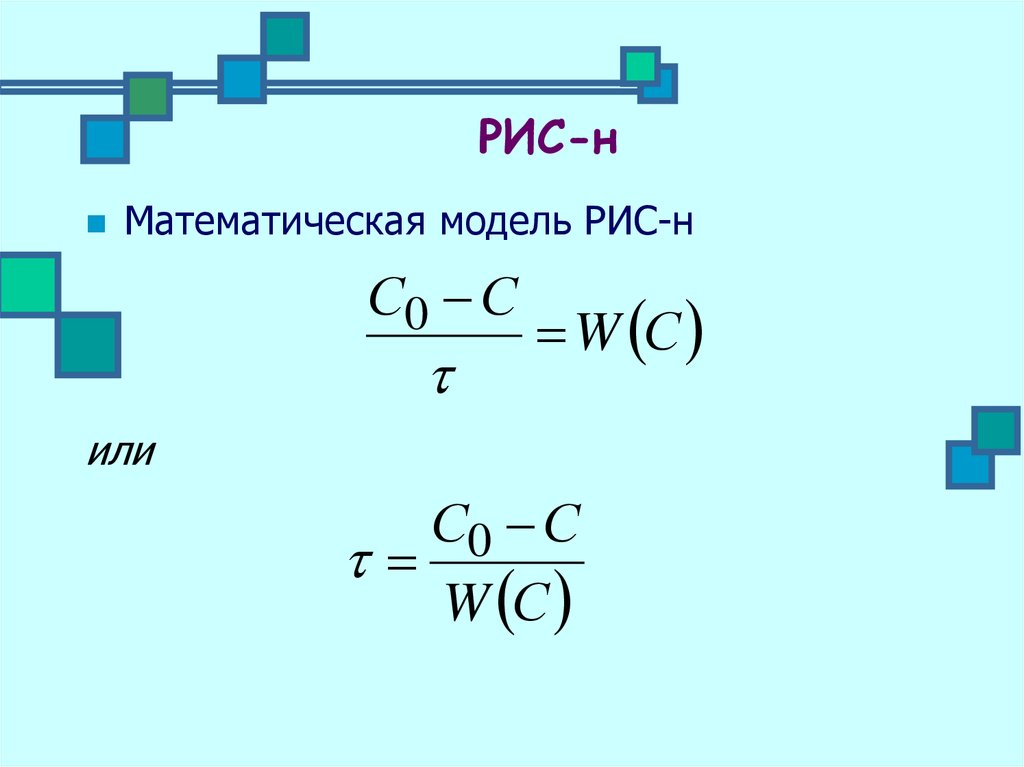
17. РИС-н

Математическая модель РИС-н
С0 С
W С
или
С0 С
W С

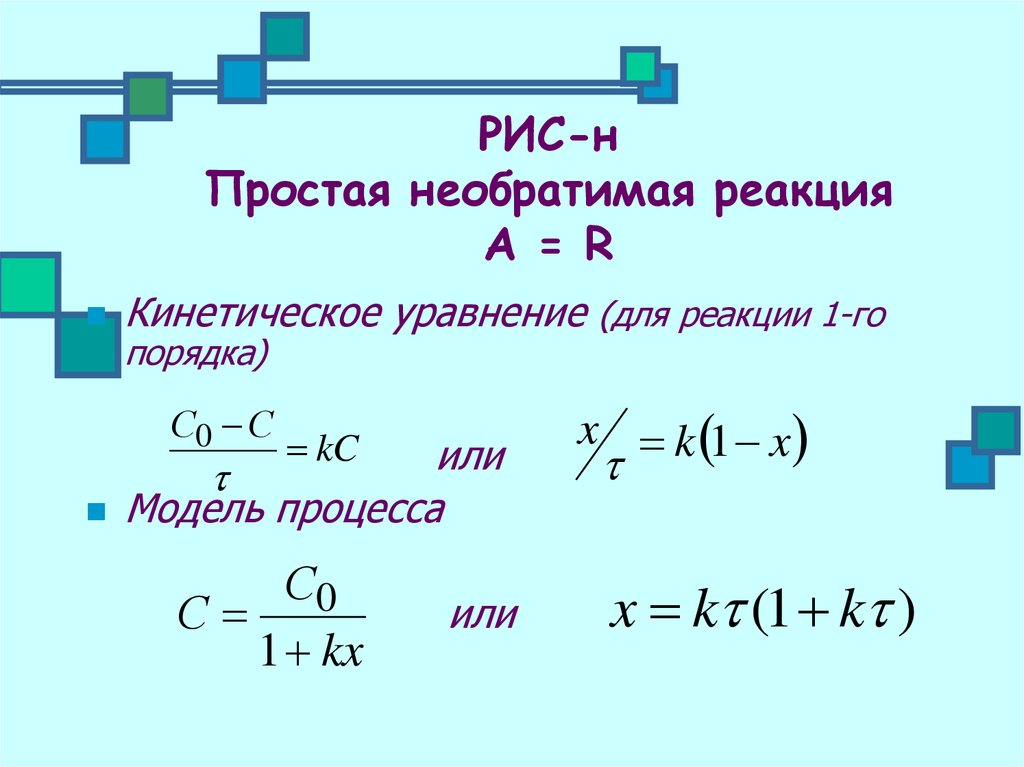
18. РИС-н Простая необратимая реакция А = R

Кинетическое уравнение (для реакции 1-го
порядка)
С0 С
kC
или
Модель процесса
С0
С
1 kx
или
x k 1 x
x k (1 k )

19. РИС-н Простая необратимая реакция А = R

При заданном значении нагрузки V0
время реакции – фиксированная
Vp
величина
,
V0
концентрация реагентов при постоянном С0
во всем объеме одинакова и равна С
(область перехода от С0 до С на входе
очень мала, ею можно пренебречь)

20. РИС-н Простая необратимая реакция А = R

Зависимость С( )
Зависимость С( )
получают
изменением Vр
при V0 = соnst , или
нагрузки V0
при Vр = соnst

21. РИС-н Простая обратимая реакция А = R

Кинетическое уравнение (для реакций 1-го порядка
в обоих направлениях)
W(C) = k1CА – k2CR
Модель процесса
С0 С
или
k1C А k 2C R или
k1
x
1 k1 k2
х k 1 x k x
2
1

22. РИС-н Простая обратимая реакция А  R

РИС-н
Простая обратимая реакция
А R
При →∞ достигается равновесие и конверсия равна
k1
хр
k1 k 2
Равновесная конверсия в РИС-н совпадает с хр в РИВ
Следовательно, зависимость х( ) и влияние на нее
условий процесса, будут такими же, как и в режиме
РИВ

23. Сопоставление РИВ и РИС-н

Зависимость
концентрации С в РИВ
и РИС-н
Из графика видно:
РИВ РИС и VРИВ < VРИС

24. Сопоставление РИВ и РИС-н

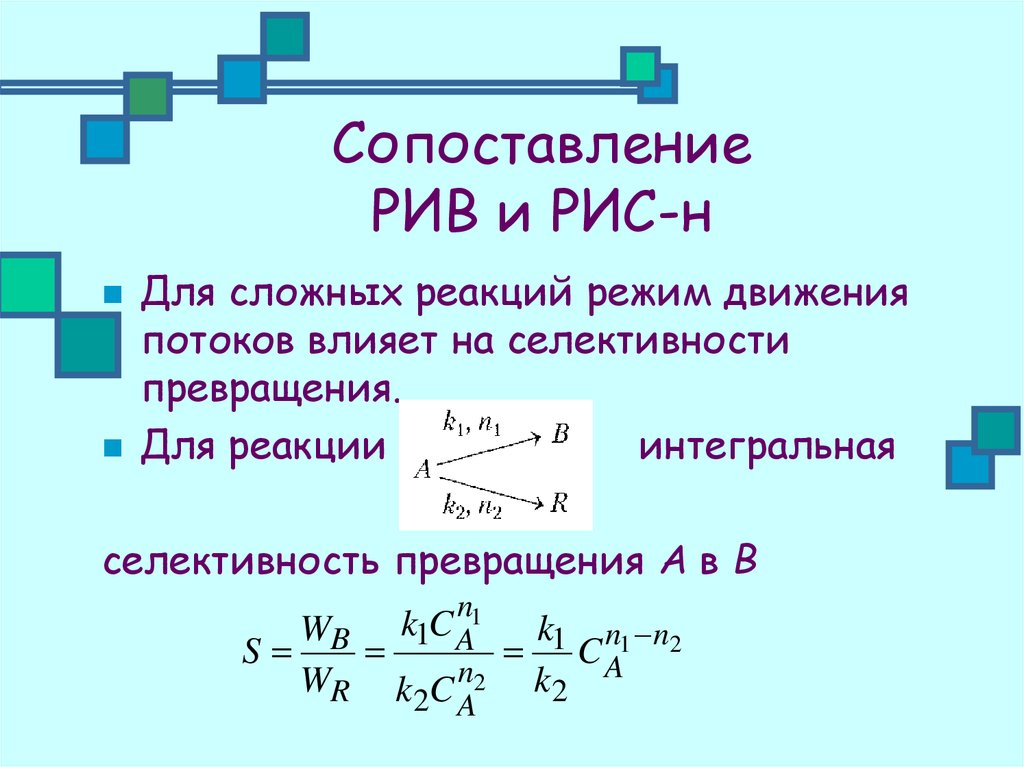
Для сложных реакций режим движения
потоков влияет на селективности
превращения.
Для реакции
интегральная
селективность превращения А в В
n
k1C A1
WB
k1 n1 n2
S
CA
n
WR k C 2 k2
2 A

25. Сопоставление РИВ и РИС-н

Следовательно, при проведении процесса
в РИВ и РИС возможны три варианта:
SРИВ = SРИС для n1 = n2;
SРИВ SРИС для n1 > n2;
SРИВ SРИС для n1 n2

26. Сопоставление РИВ и РИС-н

Таким образом, процесс в РИВ всегда
интенсивнее,
а при n1 > n2 и n1 = n2 - селективность его выше,
чем в РИС.
При n1 n2 увеличение селективности в РИВ
достигается за счет некоторого снижения
интенсивности процесса.
РИС удобен для процессов с медленной
реакцией, когда в емкостях с перемешиванием
можно обеспечить достаточно большое .