Определение и виды сортировки

1. Сортировки

2. Определение сортировки

Сортировка - процесс упорядочения множества подобных
информационных объектов в некотором определённом порядке
с целью облегчения последующего поиска нужных элементов.

3. Виды сортировки

Сортировки, в зависимости от типа сортируемого объекта,
можно разделить на 2 вида:
Сортировка файлов
Сортировка массивов

4. Сортировка массивов

• Внутренняя сортировка, или сортировка массивов,
оперирует массивами, целиком помещающимися в
оперативной памяти с произвольным доступом к любой
ячейке.
• Данные обычно упорядочиваются на том же месте без
дополнительных затрат памяти.

5. Сортировка файлов

• Внешняя сортировка, или сортировка файлов, оперирует
запоминающими устройствами большого объёма.
• Доступ к носителю осуществляется последовательным
образом: в каждый момент времени можно считать или
записать только элемент, следующий за текущим.
• Объём данных не позволяет им разместиться в ОЗУ.
• Это приводит к специальным методам упорядочения,
обычно использующим дополнительное дисковое
пространство.

6. Критерии оценки алгоритмов

• Время или вычислительная сложность— основной параметр,
характеризующий быстродействие алгоритма.
Идеальное поведение для упорядочения — O(n).
Алгоритмы сортировки, использующие только операцию
сравнения всегда нуждаются в O(n log n) сравнениях.
• Память — ряд алгоритмов требует выделения
дополнительной памяти под временное хранение данных.
Алгоритмы сортировки, не потребляющие дополнительной
памяти, относят к сортировкам на месте.

7. Свойства алгоритмов сортировки

• Устойчивость
• Естественность поведения
• Использование операции сравнения

8. 2 подхода к сортировке массивов

Устойчивость — устойчивая сортировка не меняет взаимного
расположения элементов с одинаковыми ключами
Простые способы сортировки соответствуют устойчивой
сортировке, улучшенные - неустойчивой.
Простые способы
Улучшенные способы

9. Список простых способов сортировки

Список простых, или устойчивых, способов сортировки:
• Сортировка вставками - O(n^2)
• Сортировка выбором - O(n^2)
• Пузырьковая сортировка - O(n^2)
o Гномья сортировка - O(n^2)
o Сортировка слиянием - O(n log n)
o Сортировка подсчётом - O(n+k)
o Блочная сортировка - O(n)

10. Список улучшенных способов сортировки

Список улучшенных, или неустойчивых, способов:
• Быстрая сортировка, или QuickSort - O(n log n) - O(n^2)
• Сортировка Шелла, или ShellSort - O(n log^2 n)
• Пирамидальная сортировка, или HeapSort - O(n log n)
o Сортировка расчёской, или ComsSort - O(n log n)
o Плавная сортировка, или SmoothSort - O(n log n)
o Интроспективная сортировка, или IntroSort - O(n log n)
o Терпеливая сортировка, или PatienceSort - O(n log n)
o Поразрядная сортировка - O(nk)

11. Сортировка вставками

Сортировка вставками — алгоритм сортировки, в котором
элементы исходной последовательности просматриваются по
одному, и каждый новый поступивший элемент размещается в
подходящее место среди ранее упорядоченных элементов
Разновидности:
• Простые вставки
• Вставки с барьерным элементом
• Бинарные вставки или вставки методом бинарного поиска

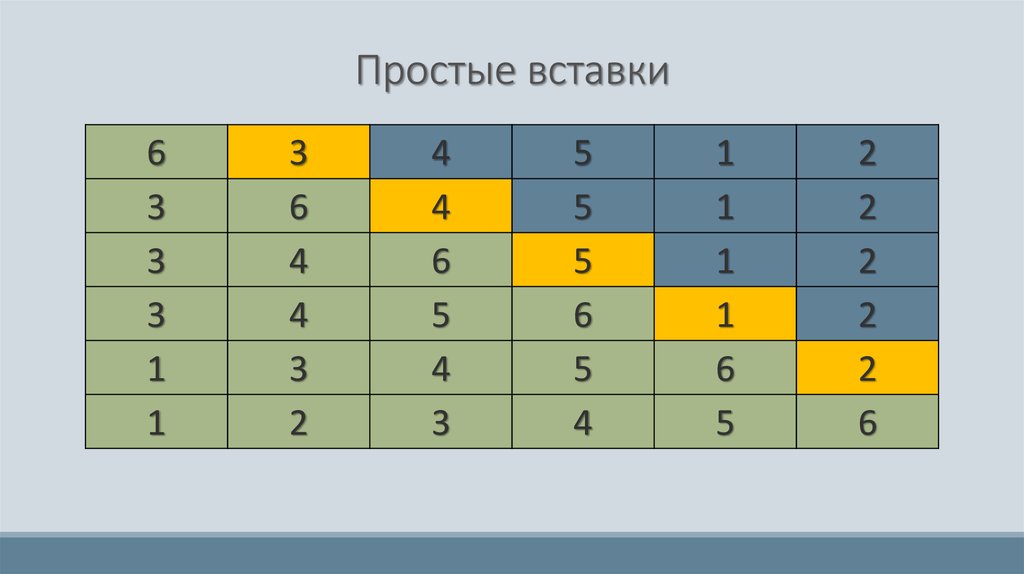
12. Простые вставки

6
3
3
3
1
1
3
6
4
4
3
2
4
4
6
5
4
3
5
5
5
6
5
4
1
1
1
1
6
5
2
2
2
2
2
6

13. Простые вставки

14. Простые вставки

Алгоритм состоит из (n-1)-го прохода, каждый из которых включает 4
действия:
• Взятие очередного i-го неотсортированного элемента и сохранение его
• Поиск позиции j в отсортированной части массива, в которой
присутствие взятого элемента не нарушит упорядоченности
• Сдвиг элементов от j-го до (i-1)-го вправо, чтобы освободить позицию
для вставки
• Вставка взятого элемента в найденную j-ую позицию

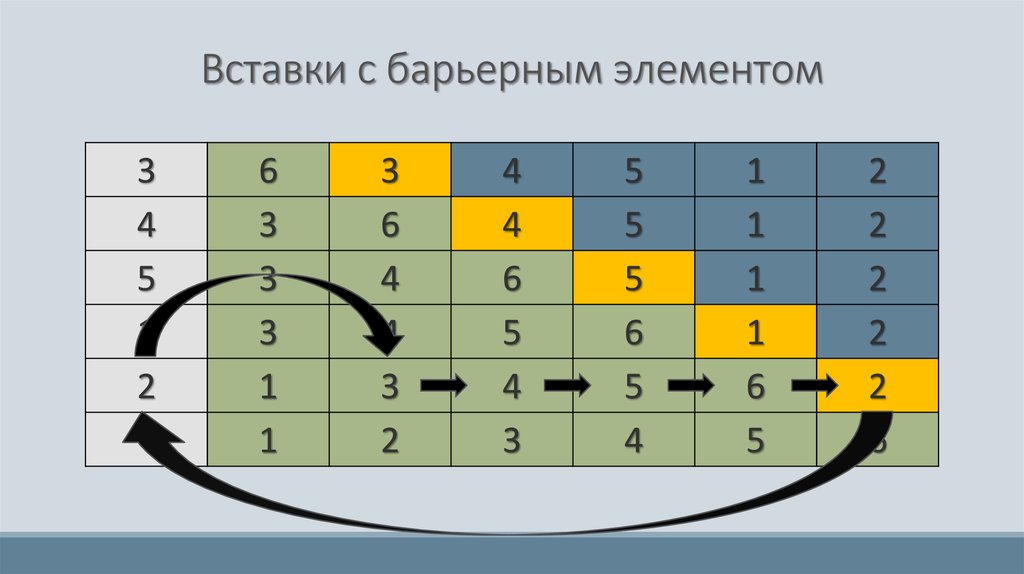
15. Вставки с барьерным элементом

3
4
5
1
2
6
3
3
3
1
1
3
6
4
4
3
2
4
4
6
5
4
3
5
5
5
6
5
4
1
1
1
1
6
5
2
2
2
2
2
6

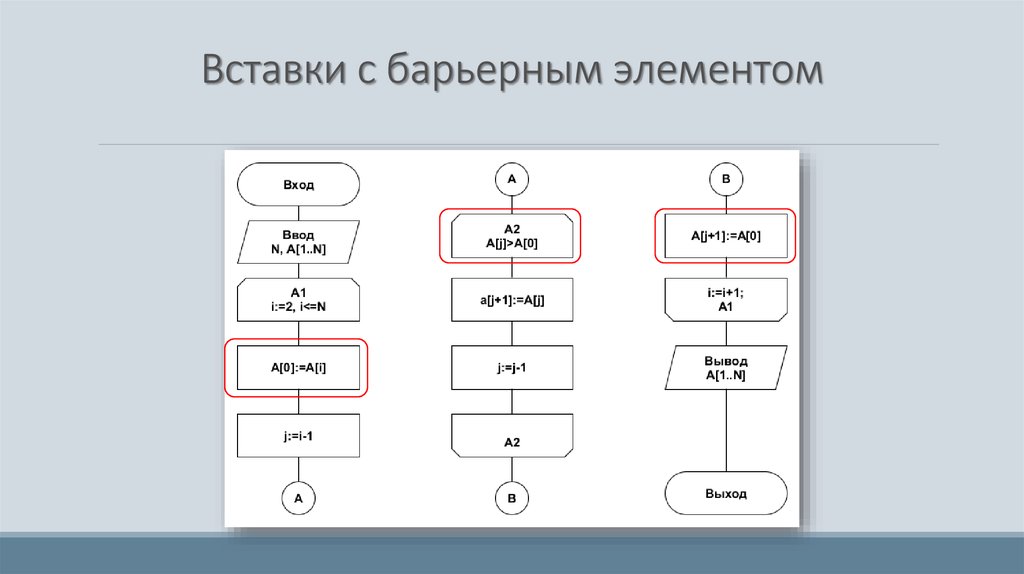
16. Вставки с барьерным элементом

17. Вставки с барьерным элементом

Введение барьерного элемента позволяет отказаться от
проверки условия выхода за пределы массива, т. к. условие
остановки при поиске места для элемента определяется
следующим правилом: слева меньшие или равные
вставляемому элементу, а справа строго большие его.

18. Метод бинарного поиска элемента

Бинарный поиск - классический алгоритм поиска элемента в
отсортированном массиве, использующий дробление
массива на половины.
5
1
LEFT
10
2
15
3
20
4
25
5
30
6
35
7
40
8
45
9
50
10
RIGHT

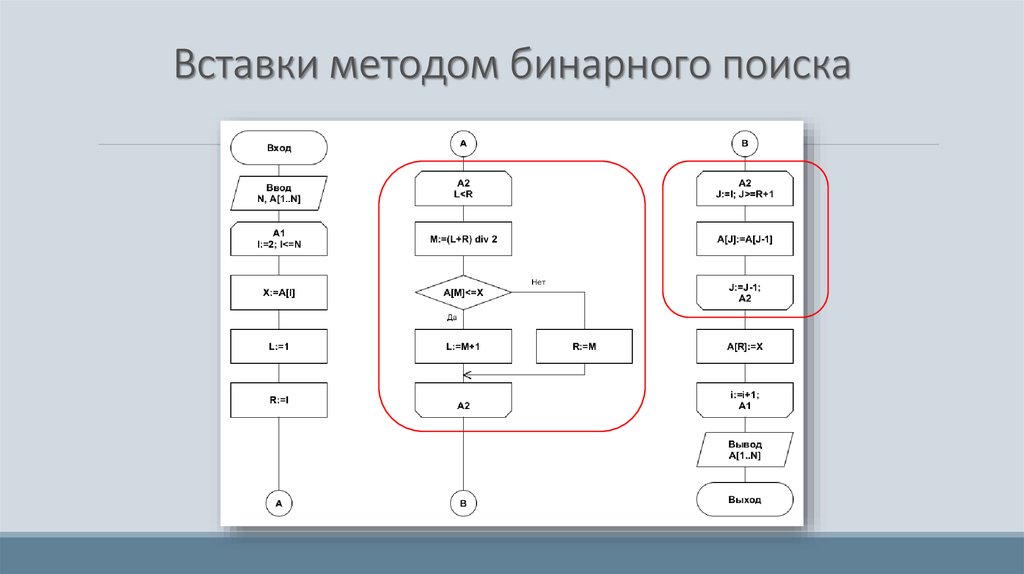
19. Вставки методом бинарного поиска

6
3
3
3
1
1
3
6
4
4
3
2
4
4
6
5
4
3
5
5
5
6
5
4
1
1
1
1
6
5
2
2
2
2
2
6

20. Вставки методом бинарного поиска

21. Вставки методом бинарного поиска

Особенности метода:
• Неестественность поведения – если элементы в
исходном массиве расположены в обратном порядке, то
потребуется минимальное количество сравнений, если
же массив уже упорядочен, то максимальное
• Данный метод не меняет количества необходимых
перестановок, а только количество сравнений

22. Сортировка выбором

Метод прямого выбора в некотором смысле
противоположен методу прямой вставки.
При прямой вставке на каждом шаге рассматривается
только один очередной элемент исходной
последовательности.
При прямом выборе для поиска одного минимального
элемента просматриваются все элементы исходной
неотсортированной последовательности.

23. Сортировка выбором

6
1
1
1
1
1
3
3
2
2
2
2
4
4
4
3
3
3
5
5
5
5
4
4
1
6
6
6
6
5
2
2
3
4
5
6

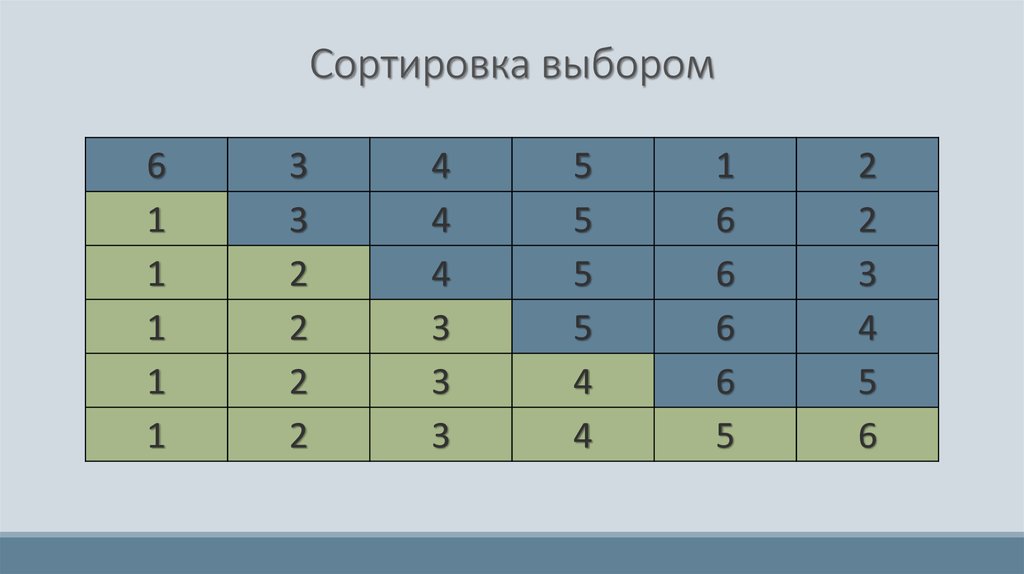
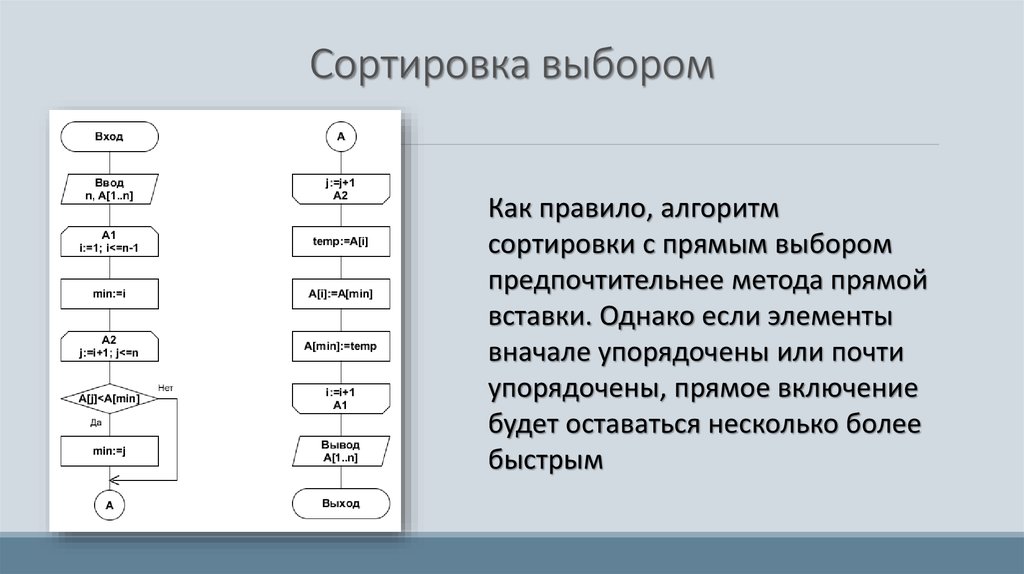
24. Сортировка выбором

Как правило, алгоритм
сортировки с прямым выбором
предпочтительнее метода прямой
вставки. Однако если элементы
вначале упорядочены или почти
упорядочены, прямое включение
будет оставаться несколько более
быстрым

25. Сортировка выбором

Порядок шагов для сортировки:
1. Выбрать минимальный элемент из всего исходного
массива и поместить его на первое место, а первый
элемент – на место минимального
2. Просматривая массив от второго элемента до конца,
найти минимальный элемент и поместить его на второе
место, а второй на место минимального.
3. Повторять эту операцию для каждого элемента кроме
последнего

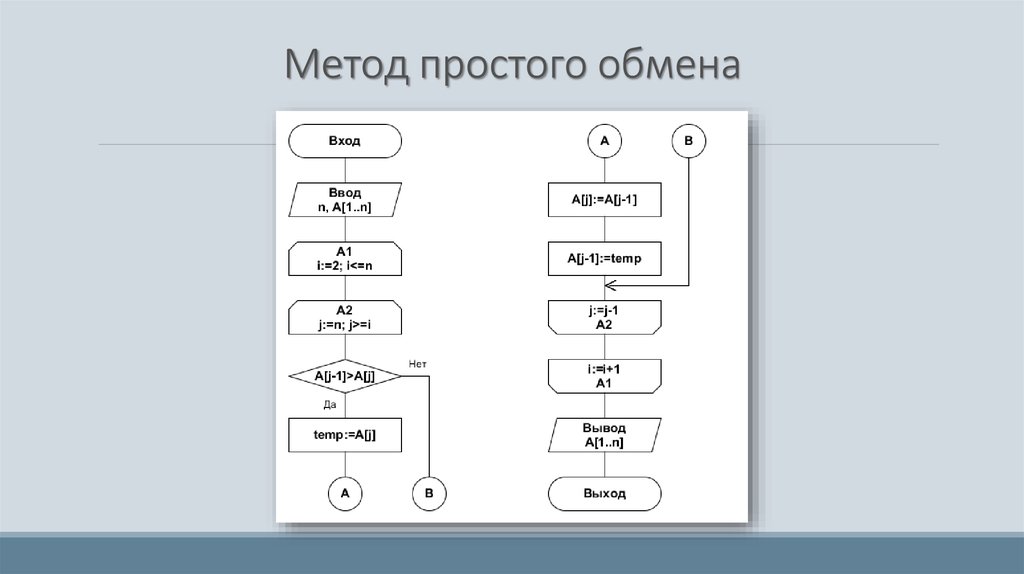
26. Методы сортировки обменом

Сущность этого метода отражена в названии. Самые «легкие» элементы
массива «всплывают», а самые «тяжелые» - «тонут». Необходимо
просмотреть весь массив и менять стоящие рядом элементы в том случае,
если они стоят не по порядку. Таким образом, наверх выталкивается самый
«легкий» элемент. Это повторяется для оставшихся элементов массива.
Разновидности:
• Метод простого обмена (Пузырёк)
• Пузырёк с флажком
• Метод «Плавающего пузырька»
• Шейкерная сортировка

27. Метод простого обмена

6
1
1
1
1
1
1
3
6
2
2
2
2
2
4
3
6
3
3
3
3
5
4
3
6
4
4
4
1
5
4
4
6
5
5
2
2
5
5
5
6
6

28. Метод простого обмена

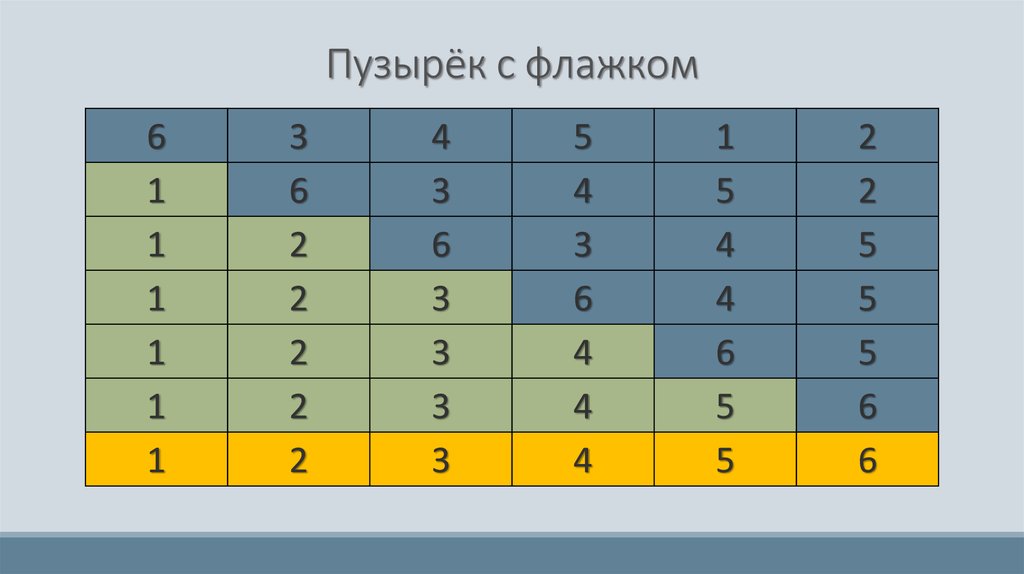
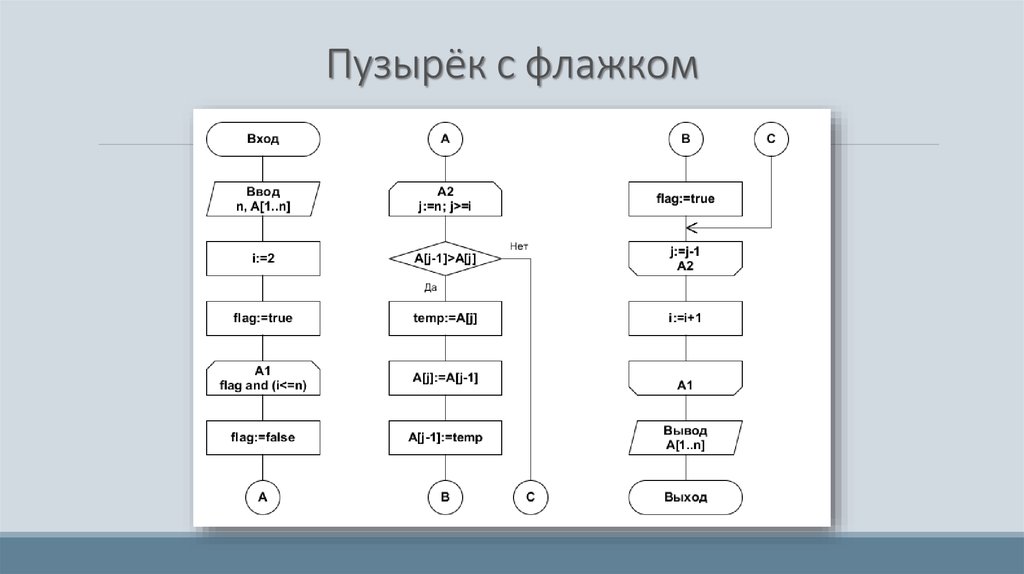
29. Пузырёк с флажком

При реализации сортировки методом обмена приходится
выполнять одиночные проходы n-1 раз. Этого можно
избежать, если перед проведением очередного прохода
проверять, была ли произведена перестановка на
предыдущем проходе. Для этого нужно ввести
вспомогательную переменную «флажок». Если
перестановки не было, значит массив упорядочен и
сортировку можно прекратить.

30. Пузырёк с флажком

6
1
1
1
1
1
1
3
6
2
2
2
2
2
4
3
6
3
3
3
3
5
4
3
6
4
4
4
1
5
4
4
6
5
5
2
2
5
5
5
6
6

31. Пузырёк с флажком

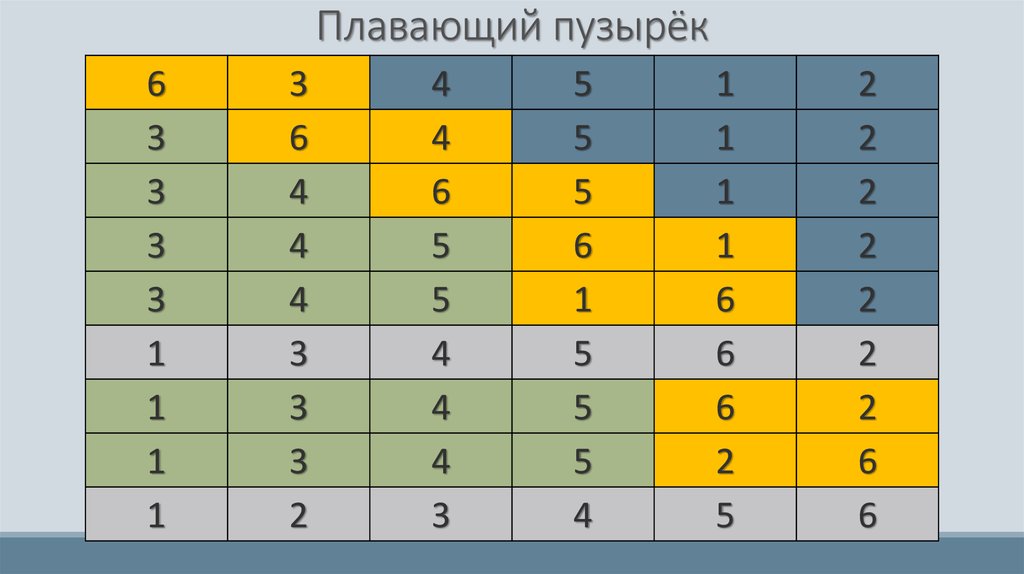
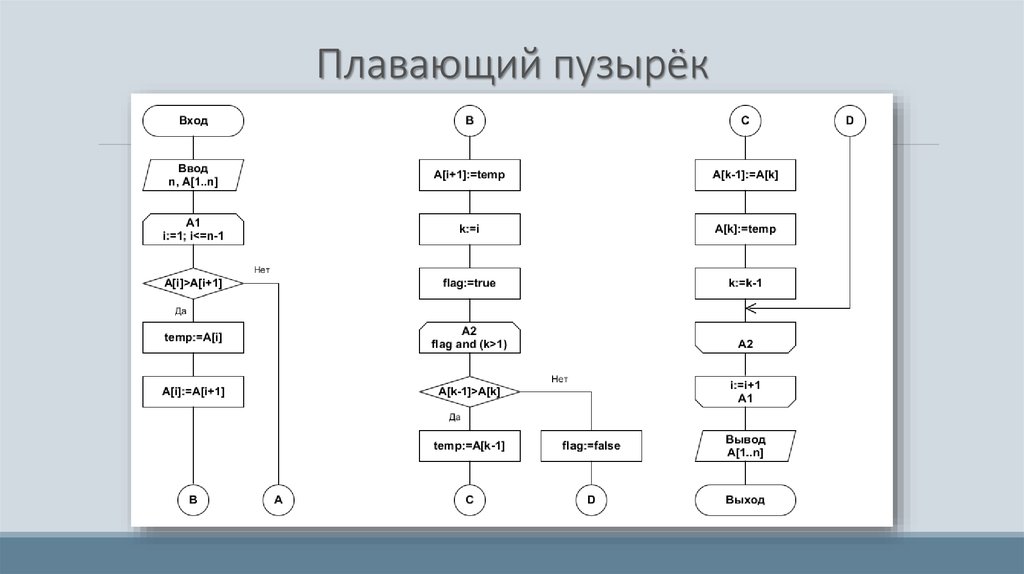
32. Плавающий пузырёк

Если на некотором шаге выполняется просмотр i-го элемента и
слева от него имеется уже упорядоченная последовательность
элементов, то в конечном счете i-й элемент займет любую позицию
от 1-й до i-й. Выполняется движение к концу массива, до тех пор,
пока не обнаружится нарушение сортирующего условия. После
соответствующего обмена элементов начинается движение в
обратном направлении до тех пор, пока выполняются
необходимые обмены элементов. Если обменов при обратном
движении уже нет, то движение продолжается с места остановки.
Описанная процедура повторяется до тех пор, пока не будет
достигнут конец массива.

33. Плавающий пузырёк

6
3
3
3
3
1
1
1
1
3
6
4
4
4
3
3
3
2
4
4
6
5
5
4
4
4
3
5
5
5
6
1
5
5
5
4
1
1
1
1
6
6
6
2
5
2
2
2
2
2
2
2
6
6

34. Плавающий пузырёк

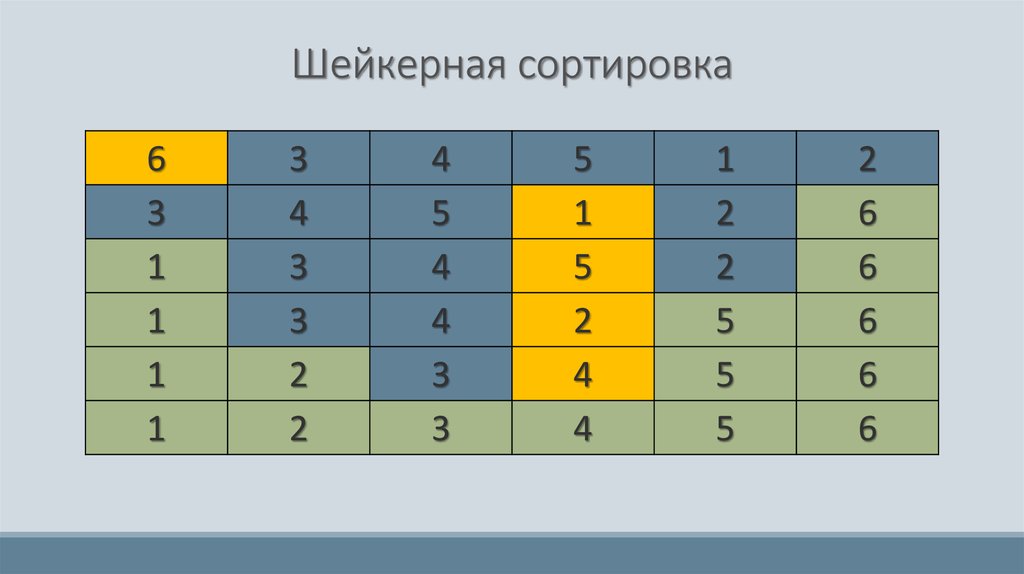
35. Шейкерная сортировка

Легко увидеть, что в алгоритме сортировки “пузырьком” “легкие
пузырьки” всплывают за один проход, а “тяжелые” – тонут за
несколько. Такая асимметрия вызвала появление новой идеи
сортировки, “пузырьком”, а именно: сортировать не в одну
сторону, а поочередно в обе, т.е. на каждом шаге осуществляется
проход как в одну сторону, так и в другую. Таким образом, на
каждом шаге “легкий пузырек” всплывает на поверхность, а
“тяжелый” – тонет.

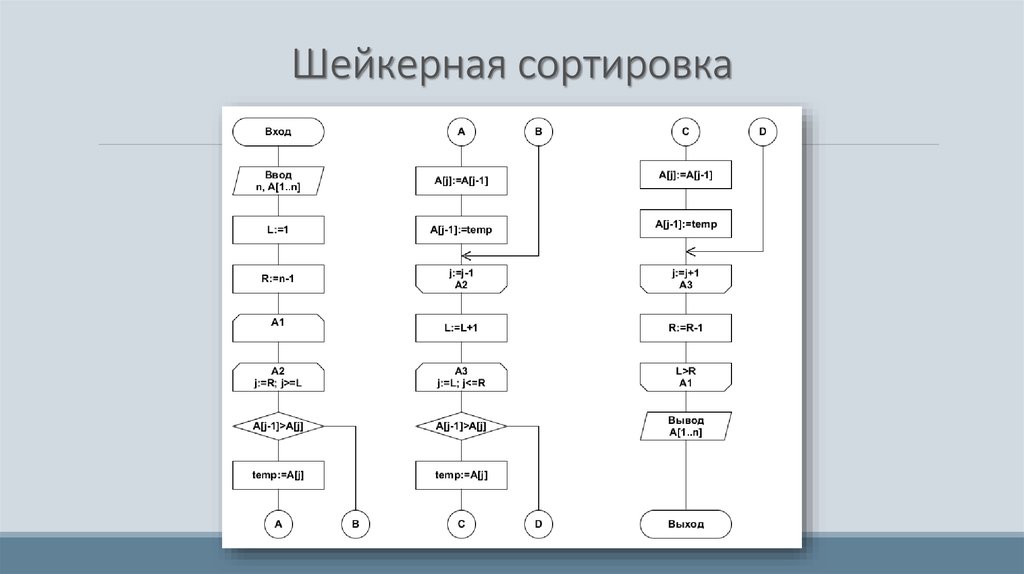
36. Шейкерная сортировка

6
3
1
1
1
1
3
4
3
3
2
2
4
5
4
4
3
3
5
1
5
2
4
4
1
2
2
5
5
5
2
6
6
6
6
6

37. Шейкерная сортировка

38. Домашнее задание

В массиве А[100], содержащем целые положительные числа,
найти сумму максимального количества чисел, при этом их
произведение не должно превышать число 300.