Основные понятия информатики

1. Основные понятия информатики

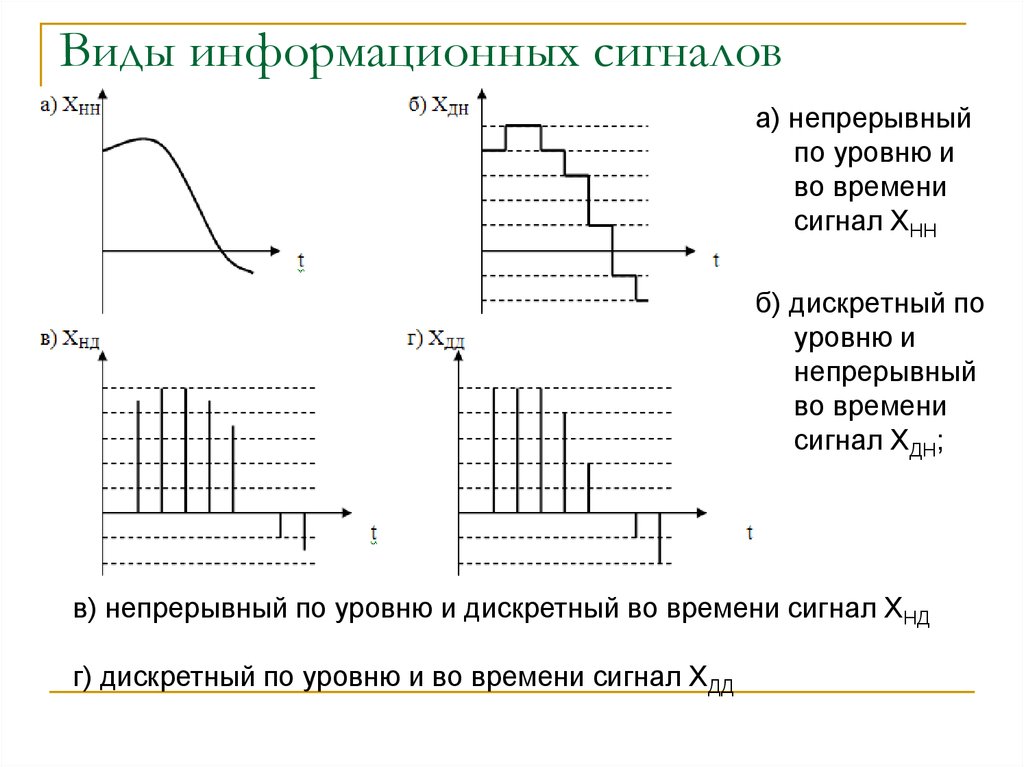
2. Виды информационных сигналов

а) непрерывный
по уровню и
во времени
сигнал ХНН
б) дискретный по
уровню и
непрерывный
во времени
сигнал ХДН;
в) непрерывный по уровню и дискретный во времени сигнал ХНД
г) дискретный по уровню и во времени сигнал ХДД

3. Понятие количества информации:

1Кб = 1024 байта = 210 (1024) байтов
1Мб = 1024 Кб = 220 (1024 1024) байтов
1Гб = 1024 Мб = 230 (1024 1024 1024)
байтов
1Тб=1024Гб= 240 (1024 1024 1024
1024) байтов

4. Системы счисления

Позиционная
Непозиционная
(0,1,2, …, 9)
(IV, VI, XIV )

5.

В общем случае запись любого числа в позиционной
системе счисления с основанием Р можно
представить в виде:
am-1Pm-1 +am-2Pm-2 + … +a1P1 + a0P0 + a-1P-1 + a-2P-2 + … +a-sP-s

6. Десятичная система счисления основание Р=10

1) десятичное число 1784 можно
представить как
1*103 + 7*102 + 8*101 + 4*100
2)десятичное число 78,14 можно
представить как
7*101 + 8*100 + 1*10-1 + 4*10-2.

7. Двоичная система счисления основание Р=2

Например
Перевести число из двоичной системы
счисления в десятичную:
101110,101 (2) =1*25 + 0*24 + 1*23 + 1*22 +1*21
+0*20 +1*2-1 + 0*2-2 + 1*2-3 =46,625(10)

8.

В вычислительных машинах применяются две
формы представления двоичных чисел:
форма с фиксированной запятой
(естественная форма)
форма с плавающей запятой (нормальная
форма)

9. С фиксированной запятой

Примеры:
+0987,12300;
+00000,11119;
-99991,00234

10. С плавающей запятой

каждое число изображается в виде двух
групп цифр: мантиссы и порядка ,
где
М – мантисса числа по модулю, она должна
быть меньше 1 (|М|<1);
r - порядок числа (r- целое число);
Р – основание системы счисления.

11. Примеры :

1) +987,12300 можно представить как
0,987123*103
М=0,987123, порядок r=3
2) +0,000119 можно представить как 0,119*10-3
М=0,119, порядок r = -3
3) -99991,0234 можно представить как
-0,999910234*105
М= -0,999910234, порядок r = 5

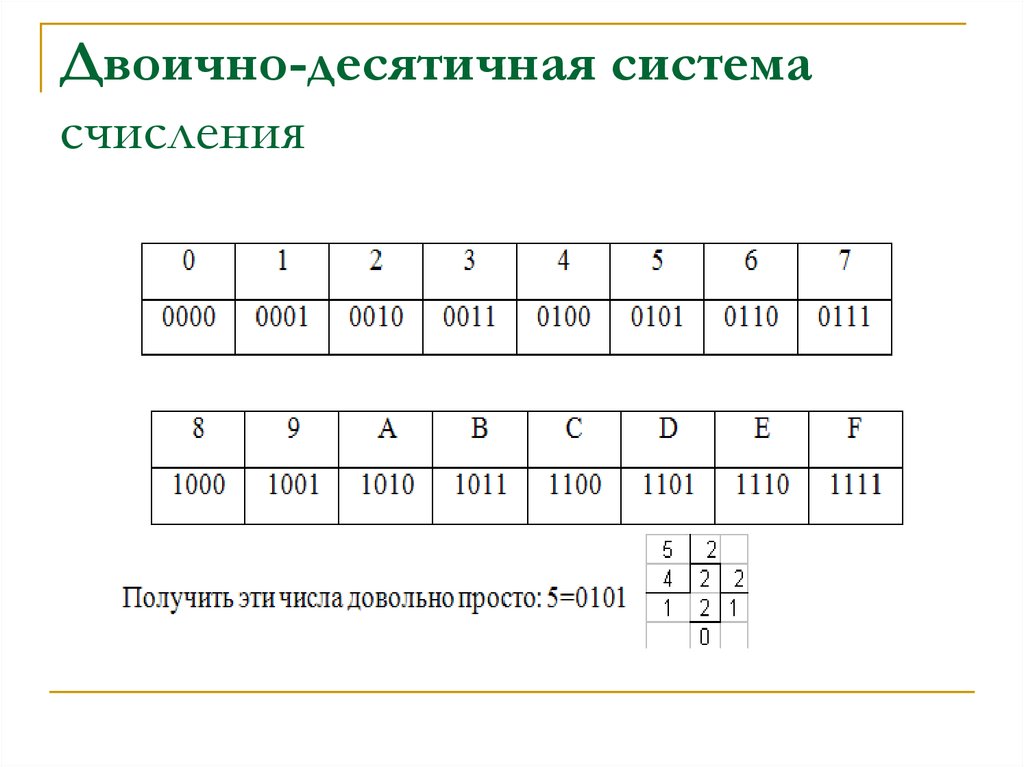
12. Двоично-десятичная система счисления

13. Шестнадцатеричная система счисления

Для изображения цифр больших 9 в
шестнадцатеричной системе счисления применяются
буквы:
А – 10, B – 11, C – 12, D – 13, E – 14, F – 15.
Например
Шестнадцатеричное число F17B в двоичной системе
выглядит так: 1111000101111011

14. Примеры перевода чисел из одной системы счисления в другую

15.

Пример1. Перевести двоичное число
10111 в десятичное
101112=1*24 + 0*23 + 1*22 +1*21 +1*20=16+4+2+1=2310

16.

Пример2. Перевести десятичное число
111 в двоичное. 111 2
110 55 2
1 54 27 2
1 26 13
1 12
1
2
6
6
0
2
3
2
1
2
1
Получилось число 1101111, т.е. 11110=11011112
Проверим это:
11011112=1*26+1*25+0*24+1*23+1*22+1*21+1*20=
= 64+32+8+4+2+1=11110

17.

Пример3. Перевести десятичное число
703 в двоично-десятичное.
На каждый десятичный разряд отводится
четыре позиции в соответствии с таблицей
7 – 0111
0 – 0000
3 – 0011
получаем, что 70310=0111 0000 00112-10

18.

Пример4. Перевести двоично-десятичное
число 1001 1000 0001 0101 в десятичное,
используя таблицу перевода.
1001 – 9
1000 – 8
0001 – 1
0101 – 6
получаем, что 1001 1000 0001 01012-10=981610

19.

Пример5. Перевести двоичнодесятичное число 1101 1111 0010 0100 в
шестнадцатеричное, используя таблицу
перевода.
1101 – D
1111 – F
0010 – 2
0100 – 4
получаем, что 1101 1111 0010 01002-10=DF2416

20. Литература:

Информатика для юристов и экономистов /
Симонович С.В. Учебник для вузов. – СПб: Питер,
2006. – 688с.
Безручко В.Т. Компьютерный практикум по курсу
"Информатика" (+CD-ROM). – гриф УМО МО РФ. - М.:
Форум (Высшее образование), 2008. – 368 с.
Информатика: Учебник / Под ред. проф. Макаровой
Н.В. – гриф УМО МО РФ. - М.: Финансы и статистика,
2007. – 768 с.