Механика материалов

1.

Белорусский государственный университет транспорта
кафедра «ЛОКОМОТИВЫ»
МЕХАНИКА МАТЕРИАЛОВ
Лекторы:
Ассистент:
д.т.н., проф. Сосновский Леонид Адамович
к.т.н., доц. Комиссаров Виктор Владимирович
асс. Таранова Е.С.
Лекции – 4 часа
Лаб. работы – 4 часа
Форма контроля знаний – экзамен
(по всем вопросам обращаться в ауд. 1415а, 1403)
ГОМЕЛЬ, 2017

2.

ЛИТЕРАТУРА
2
Основная:
1. Сосновский Л.А. Основы трибофатики: Учебное пособие для студентов технических высших
учебных заведений (допущено Министерством образования Республики Беларусь). –
Гомель: БелГУТ, 2003. – Т.1. – 246 с., – Т.2. – 234 с. (в библиотеке)
2. Сенько В.И., Сосновский Л.А. Основные идеи трибофатики и их изучение в техническом
университете. Пособие. – Гомель: БелГУТ, 2005. – 187 с. (в библиотеке)
1.
2.
3.
4.
5.
6.
7.
8.
9.
Дополнительная:
Сосновский Л.А., Комиссаров В.В. Основы трибофатики. Пособие к лекционному курсу. – Ч.1. – Гомель:
БелГУТ, 2005. – 164 с. (в продаже, БелГУТ)
Сосновский Л.А., Комиссаров В.В., Щербаков С.С. Основы трибофатики. Пособие к лекционному курсу. – Ч.2. –
Гомель: БелГУТ, 2008. – 216 с.
(в продаже, БелГУТ)
Богданович А.В., Еловой О.М., Марченко А.В., Сосновский Л.А., Тюрин С.А. Основы трибофатики.
Лабораторный практикум. – Ч.1 – Гомель: БелГУТ, 1999. – 44 с. (в библиотеке)
Сосновский Л.А., Щербаков С.С. Сюрпризы трибофатики. – Гомель: БелГУТ, 2005. – 192 с. (в библиотеке)
Sosnovskiy L.A., Sherbakov S.S. Surprises of Tribo-Fatigue. – Minsk: Magic book, 2009. – 200 p.
Слово о трибофатике. Редактор-составитель А. В. Богданович / Авт.: Ботвина Л. Р., Высоцкий М. С., Горбацевич
М. И., Грунтов П. С., Дроздов Ю. Н., Корешков В. Н., Кухарев А. В., Марченко В. А., Махутов Н. А., Павлов В.
Г., Сосновский Л. А., Старовойтов Э. И., Стражев В. И., Трощенко В. Т., Шуринов В. А., Фролов К. В., Эфрос Д.
Г. –Гомель-Минск-Москва-Киев: Rеmikа, 1996. –132 с. (в библиотеке)
Сосновский Л.А. Механика износоусталостного повреждения. – Гомель: БелГУТ, 2007. –434 с. (в библиотеке)
Сосновский Л.А. L-риск (механотермодинамика необратимых повреждений). – Гомель: БелГУТ, 2004. –317 с. (в
продаже, БелГУТ)
Фундамент и прикладн задачи тф

3.

Лекция 1
ОБЪЕМНОЕ РАЗРУШЕНИЕ:
СТАТИКА
(МЕХАНИКА МАТЕРИАЛОВ)
СОДЕРЖАНИЕ ЛЕКЦИИ:
3.1 Нагрузки.
3.2 Условие прочности. Допускаемое напряжение.
3.3 Внутренние усилия: метод сечений.
3.4 Механические свойства.
3.5 Основные типы статического разрушения.
3.6 Механические состояния. Закон Гука. Энергия деформации.
3.7 Сложное напряженное состояние.
3.8 Теории прочности. Методы расчета на прочность.

4.

3.1 НАГРУЗКА, ПРОЧНОСТЬ, ЖЕСТКОСТЬ
4
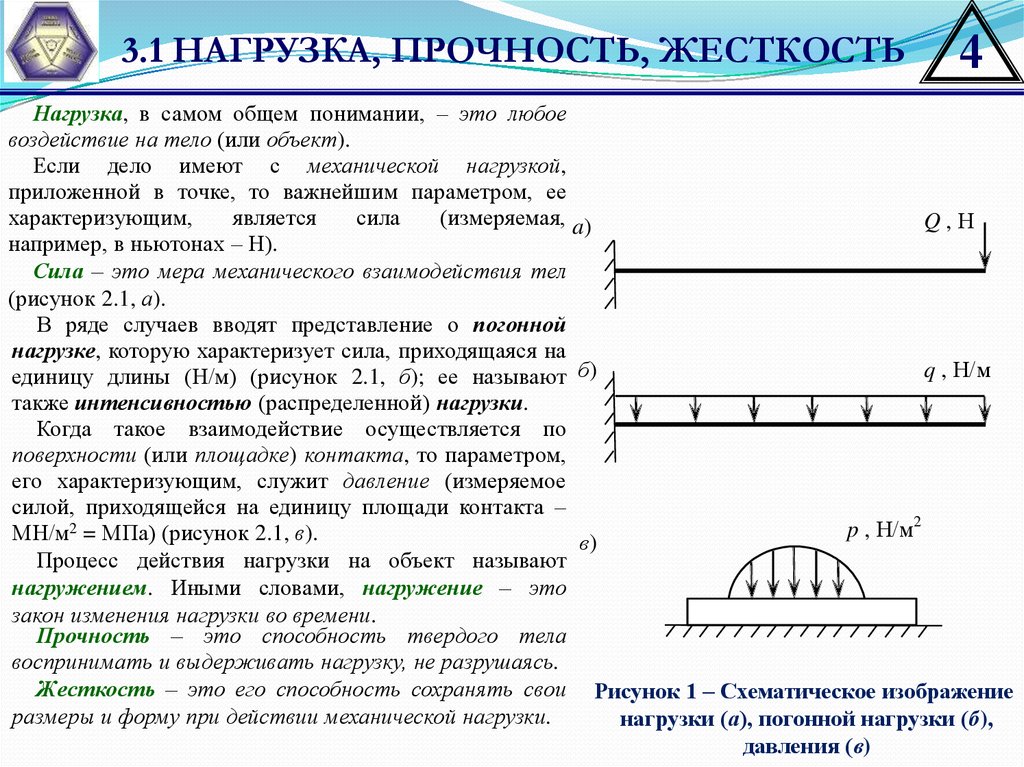
Нагрузка, в самом общем понимании, – это любое
воздействие на тело (или объект).
Если дело имеют с механической нагрузкой,
приложенной в точке, то важнейшим параметром, ее
характеризующим,
является
сила
(измеряемая, a)
Q,Н
например, в ньютонах – Н).
Сила – это мера механического взаимодействия тел
(рисунок 2.1, а).
В ряде случаев вводят представление о погонной
нагрузке, которую характеризует сила, приходящаяся на
q , Н/м
единицу длины (Н/м) (рисунок 2.1, б); ее называют б)
также интенсивностью (распределенной) нагрузки.
Когда такое взаимодействие осуществляется по
поверхности (или площадке) контакта, то параметром,
его характеризующим, служит давление (измеряемое
силой, приходящейся на единицу площади контакта –
p , Н/м2
МН/м2 = МПа) (рисунок 2.1, в).
в)
Процесс действия нагрузки на объект называют
нагружением. Иными словами, нагружение – это
закон изменения нагрузки во времени.
Прочность – это способность твердого тела
воспринимать и выдерживать нагрузку, не разрушаясь.
Жесткость – это его способность сохранять свои Рисунок 1 – Схематическое изображение
размеры и форму при действии механической нагрузки.
нагрузки (а), погонной нагрузки (б),
давления (в)

5.

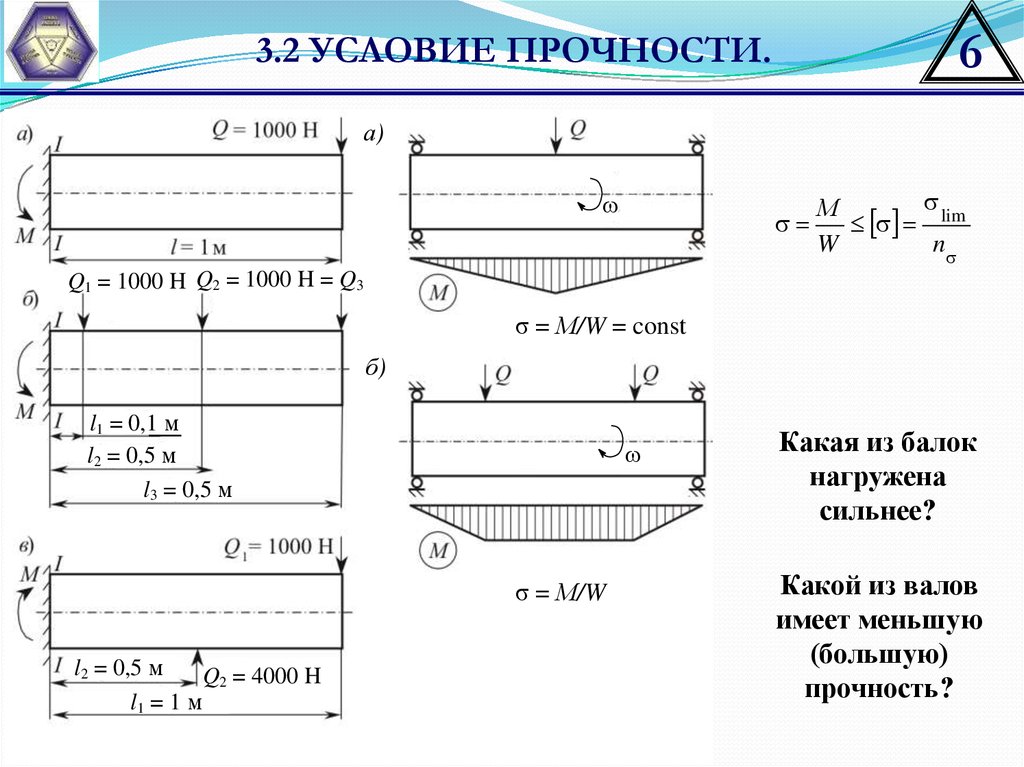
5
3.2 УСЛОВИЕ ПРОЧНОСТИ.
Условие прочности при линейном напряженном состоянии, или условие недостижения
предельного состояния, записывают так:
a)
М
Q = 1000 Н
I
I
б)
l=1м
Q1 = 1000 Н
Q 2= 600 Н= Q3
I
М
I
l 1 = 0,1 м
l3 =1 м
в)
Q1 = 1000 Н
l2 = 0,5 м
Q2 = 4000 Н
l1 = 1 м
.
(3.2)
которые называют соответственно: поверка прочности;
определение
размеров
поперечного
сечения
элемента
конструкции; выбор материала для его изготовления.
I
I
(3.1)
Используя условие (2.1) в той или иной форме, реализуют
следующие три процедуры расчетов на прочность:
max [ ] ;
W M /[ ] ;
[ ] M / W ,
l2 = 0,5 м
М
lim
.
n
Рисунок 2 – К задаче о расчете
на прочность балки при ее изгибе

6.

6
3.2 УСЛОВИЕ ПРОЧНОСТИ.
а)
М
lim
W
n
Q1 = 1000 H Q2 = 1000 H = Q3
σ = М/W = const
б)
l1 = 0,1 м
l2 = 0,5 м
l3 = 0,5 м
σ = М/W
l2 = 0,5 м
Q2 = 4000 H
l1 = 1 м
Какая из балок
нагружена
сильнее?
Какой из валов
имеет меньшую
(большую)
прочность?

7.

3.3 ВНУТРЕННИЕ УСИЛИЯ
7
Q – Qn = 0
Интенсивность внутренней силы
= Qn /A0 .
do
Сжатие
Межатомная сила
напряжение – это внутреннее усилие,
приходящееся на единицу площади (Н/м2, МПа
и др.). равнодействующая напряжений в данном
сечении и есть внутреннее усилие Qn в этом
сечении.
Рисунок 3 – К определению внутреннего
усилия в кирпиче
В
0
Растяжение d
Рисунок 4 – Изменение межатомной силы
взаимодействия
при относительном смещении двух атомов
При сжатии кирпича нагрузкой Q (см. рисунок 2.3, а)
расстояние между его атомами уменьшается на 2 10–14 см.
Смещение “всех атомов” кирпича под воздействием той
же нагрузки, то оказывается, что его сжатие (т. е.
уменьшение размера в направлении действия Q) составит
1/20000 см, что уже ощутимо.
Такая степень сжатия и возбуждает совсем не малое
результирующее внутреннее усилие Qn = 750 Н

8.

3.4 МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ
РАСТЯЖЕНИИ/СЖАТИИ
8
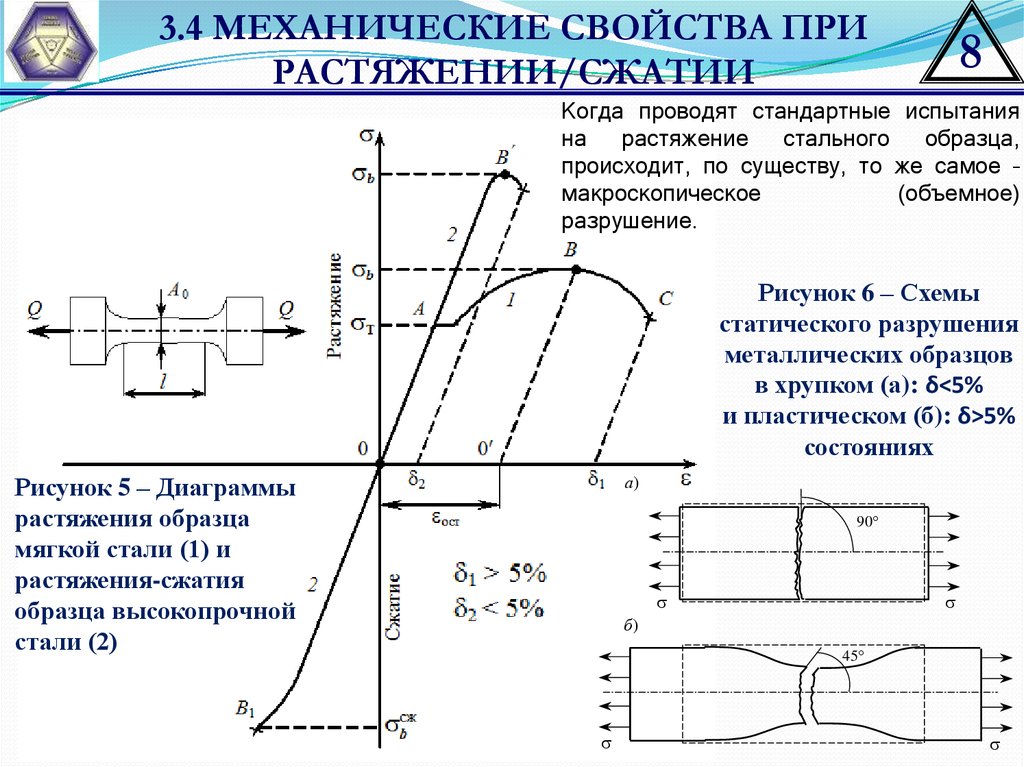
Когда проводят стандартные испытания
на
растяжение
стального
образца,
происходит, по существу, то же самое –
макроскопическое
(объемное)
разрушение.
Рисунок 6 – Схемы
статического разрушения
металлических образцов
в хрупком (а): δ<5%
и пластическом (б): δ>5%
состояниях
Рисунок 5 – Диаграммы
растяжения образца
мягкой стали (1) и
растяжения-сжатия
образца высокопрочной
стали (2)
а)
90
б)
45

9.

3.5 МЕХАНИЧЕСКИЕ СОСТОЯНИЯ.
ЗАКОН ГУКА
a)
E1
б)
9
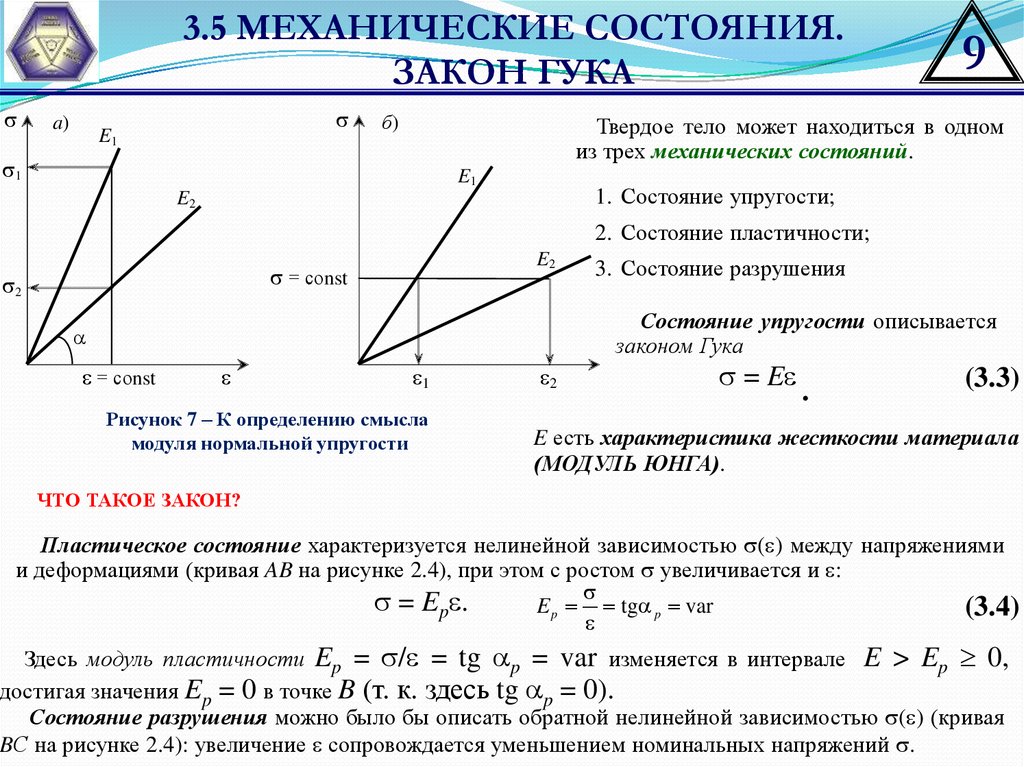
Твердое тело может находиться в одном
из трех механических состояний.
1
E1
1. Состояние упругости;
E2
2. Состояние пластичности;
E2
= соnst
2
3. Состояние разрушения
Состояние упругости описывается
законом Гука
= соnst
1
Рисунок 7 – К определению смысла
модуля нормальной упругости
2
= E
.
(3.3)
E есть характеристика жесткости материала
(МОДУЛЬ ЮНГА).
ЧТО ТАКОЕ ЗАКОН?
Пластическое состояние характеризуется нелинейной зависимостью ( ) между напряжениями
и деформациями (кривая AB на рисунке 2.4), при этом с ростом увеличивается и :
= Ep .
E p tg p var
(3.4)
Здесь модуль пластичности Ep = / = tg p = var изменяется в интервале E > Ep 0,
достигая значения Ep = 0 в точке B (т. к. здесь tg p = 0).
Состояние разрушения можно было бы описать обратной нелинейной зависимостью ( ) (кривая
BС на рисунке 2.4): увеличение сопровождается уменьшением номинальных напряжений .

10.

3.5 МЕХАНИЧЕСКИЕ СОСТОЯНИЯ.
ЗАКОН ГУКА
10
Закон Гука при сдвиге
= G ,
(3.6)
tg = a/a, << 1 и = Q/A – касательное напряжение
где относительный сдвиг
а
Q
G
a
E
2(1 )
(3.7)
G ≈ 0,4 E – МОДУЛЬ СДВИГА
Рисунок 8 – Схема чистого сдвига
Для описания трехосного напряженного состояния деформируемого твердого тела
используют интенсивность напряжения
инт
1
1 2 2 1 2 3 2 1 3 1 2
2
2
2
(3.8)
Интенсивность напряжения (3.8) связана простейшей зависимостью с октаэдрическим
касательным напряжением окт:
инт
окт
3
окт
2
1
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2
3
(3.8а)
(3.9)

11.

ОСНОВНЫЕ ВИДЫ ДЕФОРМАЦИИ
11
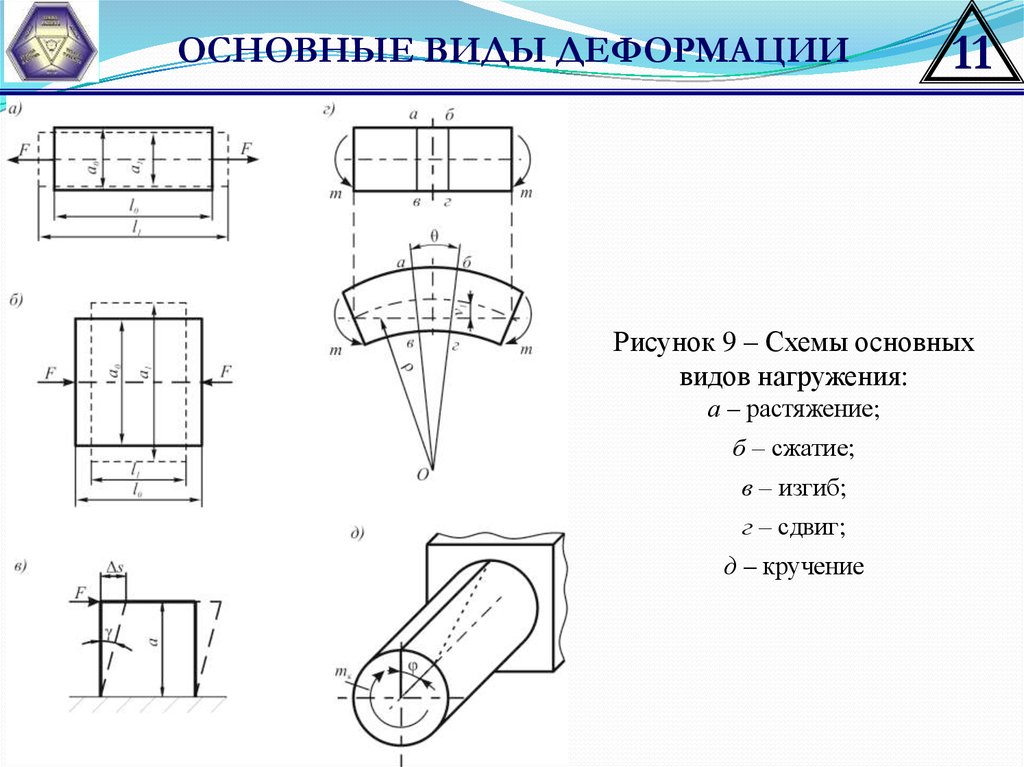
Рисунок 9 – Схемы основных
видов нагружения:
а – растяжение;
б – сжатие;
в – изгиб;
г – сдвиг;
д – кручение

12.

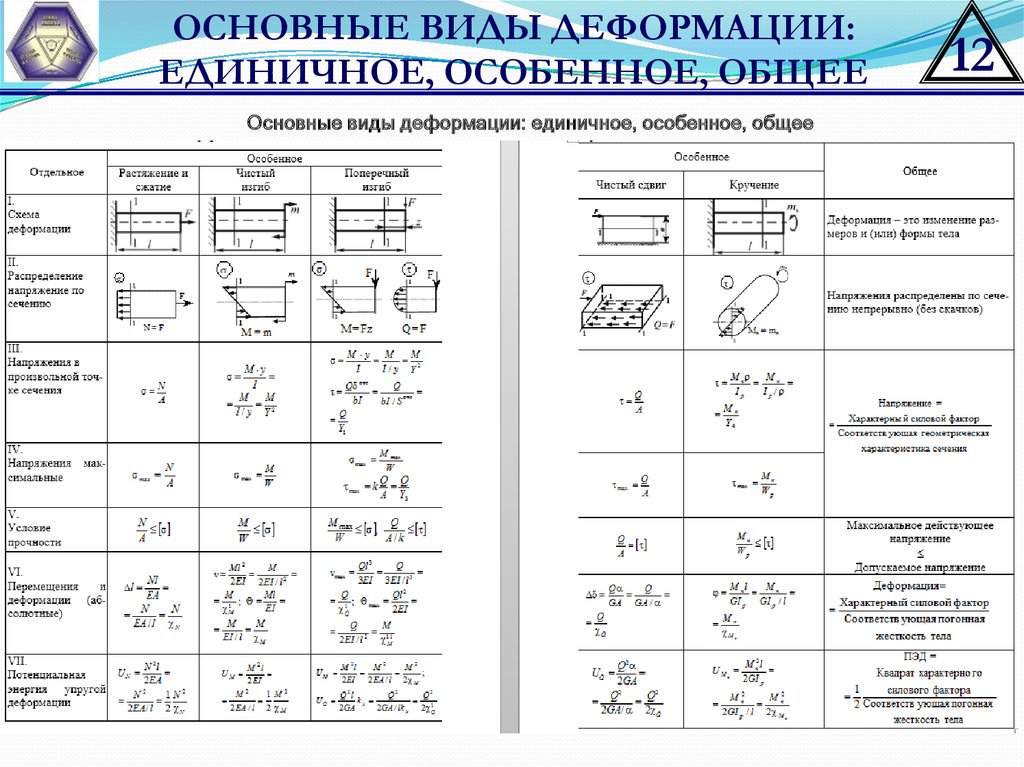
ОСНОВНЫЕ ВИДЫ ДЕФОРМАЦИИ:
ЕДИНИЧНОЕ, ОСОБЕННОЕ, ОБЩЕЕ
Основные виды деформации: единичное, особенное, общее
12

13.

ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ
НАПРЯЖЕННЫХ СОСТОЯНИЙ
Характеристики различных напряженных состояний
13

14.

ОБОБЩЕННЫЙ ЗАКОН ГУКА
14
При действии пространственной системы сил, характеризуемой главными напряжениями 1 2
3, состояние упругости описывает обобщенный закон Гука
1
1 ( 2 3 ) ;
E
1
2 2 ( 3 1 ) ;
E
1
3 3 ( 1 2 ) .
E
1
Рисунок 10 – Тензор напряжения
3
1 2G 1
ср ;
1 2
3
2 2G 2
ср ;
1 2
3
3 2G 3
ср ,
1 2
где средняя деформация
ср
1
2 3
3 1
(3.5)
(3.5а)

15.

3.6 СЛОЖНОЕ НАПРЯЖЕННОЕ
СОСТОЯНИЕ. ТЕОРИИ ПРОЧНОСТИ
15
При трехосном напряженном состоянии, которое характеризуется главными напряжениями 1
2 3, расчеты на прочность ведут по следующей схеме:
1 Теория
lim
2 проч- f ( 1, 2, 3, mj, ...) = экв
.
n
3 ности
экв
lim
(3.10)
(3.11)
n
Наиболее широкое распространение получили классические теории прочности.
экв
2 3
1 f
,
1 1
(3.12)
По первой (I), третьей (III) и четвертой (IV) теориям прочности имеем
3
III
;
экв 1 3 1 1
1
IV
экв
12 22 32 1 2 2 3 3 1
1/ 2
2 2 3 3 2 3
1
1
1 1
.
1 1
1 1 1
1
I
экв
1 ;
Пусть
(3.13)
1 2 3
эквIII ?
IV
экв ?

16.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
ТЕОРИЙ ПРОЧНОСТИ
16
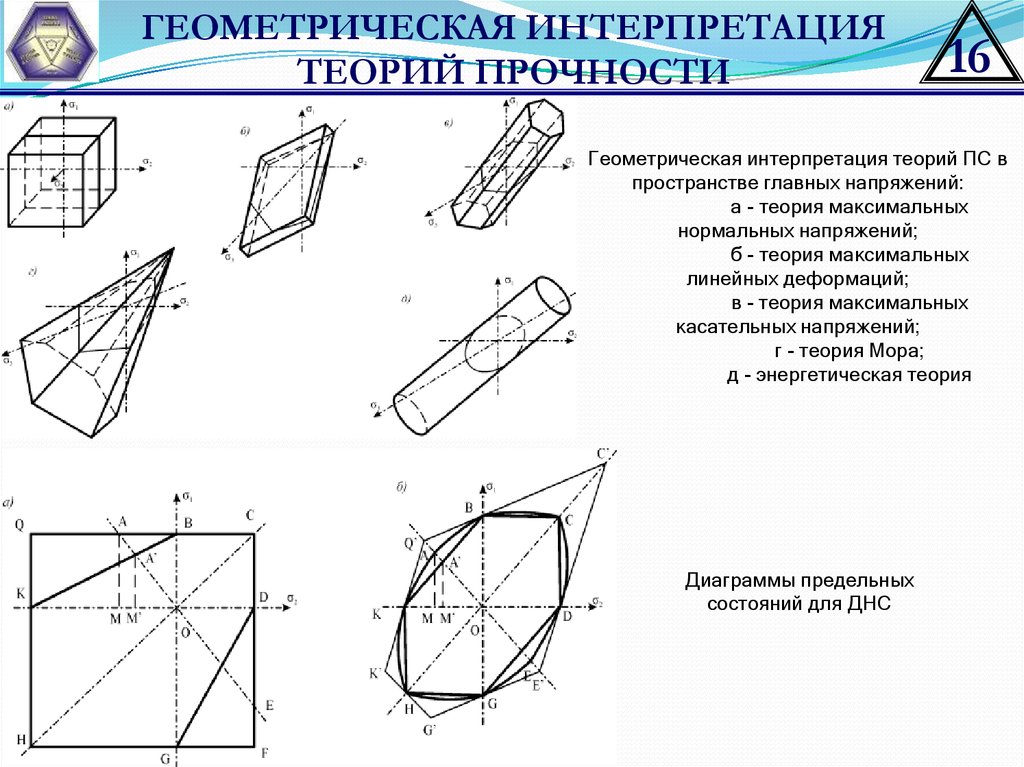
Геометрическая интерпретация теорий ПС в
пространстве главных напряжений:
а - теория максимальных
нормальных напряжений;
б - теория максимальных
линейных деформаций;
в - теория максимальных
касательных напряжений;
г - теория Мора;
д - энергетическая теория
Диаграммы предельных
состояний для ДНС

17.

ОБЗОР НЕКОТОРЫХ ТЕОРИЙ
ПРОЧНОСТИ
17
Критерии предельного состояния материалов при статическом нагружении (изотропный материал)

18.

ОБЗОР НЕКОТОРЫХ ТЕОРИЙ
ПРОЧНОСТИ
18
Критерии предельного состояния материалов при статическом нагружении (анизотропный материал)

19.

ПРИМЕР РАСЧЕТА ПРИ СЛОЖНОМ
НАПРЯЖЕННОМ СОСТОЯНИИ
19
Пример I. Определить запас прочности барабана мостового крана, в котором под действием огибающего его
каната возникают тангенциальные напряжения сжатия σ = -16 кг/мм2 (-160 МПа), максимальные напряжения
изгиба σz= ±4 кг/мм2 (±40 МПа), напряжения кручения к = 2 кг/мм2 (20 МПа). Материал барабана - серый чугун
СЧ 21-40.
Определим главные напряжения:
1
z 2 4 к2 4 16 1 4 16 2 4 22 4,2 кг 2 42МПа ;
1 z
2
2
2
2
мм
1
z 2 4 к2 4 16 1 4 16 2 4 22 16,2 кг 2 162МПа ;
3 z
2
2
2
2
мм
Интенсивность напряжений
инт 12 32 1 3 4,22 16,22 4,2 16,2 18,7
кг
187 МПа.
мм 2
Характеристики материала: предела прочности чугуна СЧ21-40 при растяжении – в 21
(210 Па), при сжатии– в 95
Эквивалентное напряжение
1
экв 1 1 1 А
1
4,2 0,75
4, 2 16, 2
18,7
1 2 3
инт
6,15
кг
мм2
0,22 18,7 1 0,22
61,5МПа ,
Коэффициент запаса прочности
n
кг
мм2
(950 МП);
в
в
кг
мм2
0,22
Так как предел прочности чугуна при сдвиге, полученный в
условиях однородного напряженного состояния, неизвестен, величину
А не представляется возможным определить расчетным путем и,
следовательно, принято его среднестатистическое значение А = 0,75.
в
21
3,4
экв 6,15
По теории максимальных нормальных деформаций
кг
экв 1 3 4,2 0,25( 16,2) 8,3 2 83МПа
в 21
мм
n
5
по теории максимальных нормальных напряжений
1 4,2
в 21
n
2,5
кг
8,3
экв 1 3 4,2 0,22( 16,2) 7,8
78
МПа
экв
мм2
Согласно теории Мора
21
n в
2,7
экв 7,8

20.

u
К РАСЧЕТУ ДОПУСКАЕМОГО
НАПРЯЖЕНИЯ
20
u
n
n
у
у
lim
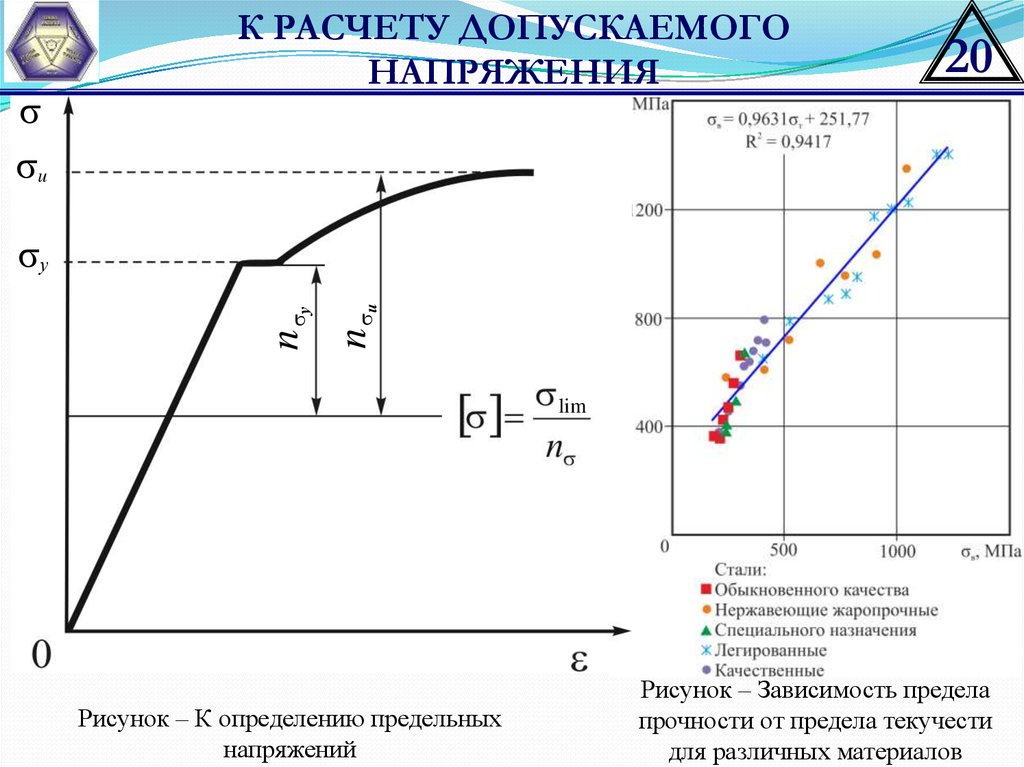
Рисунок – К определению предельных
напряжений
Рисунок – Зависимость предела
прочности от предела текучести
для различных материалов

21.

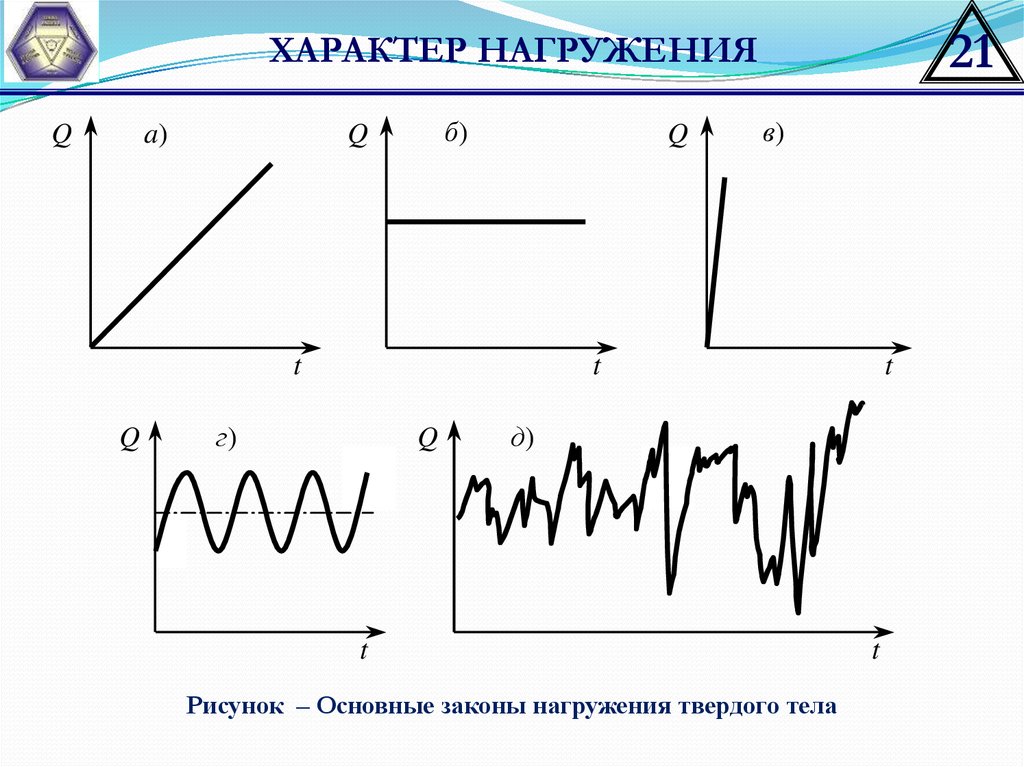
21
ХАРАКТЕР НАГРУЖЕНИЯ
a)
Q
б)
Q
Q
t
Q
в)
t
г)
Q
t
д)
t
Рисунок – Основные законы нагружения твердого тела
t