Построение сечений в многогранниках

1.

2.

3.

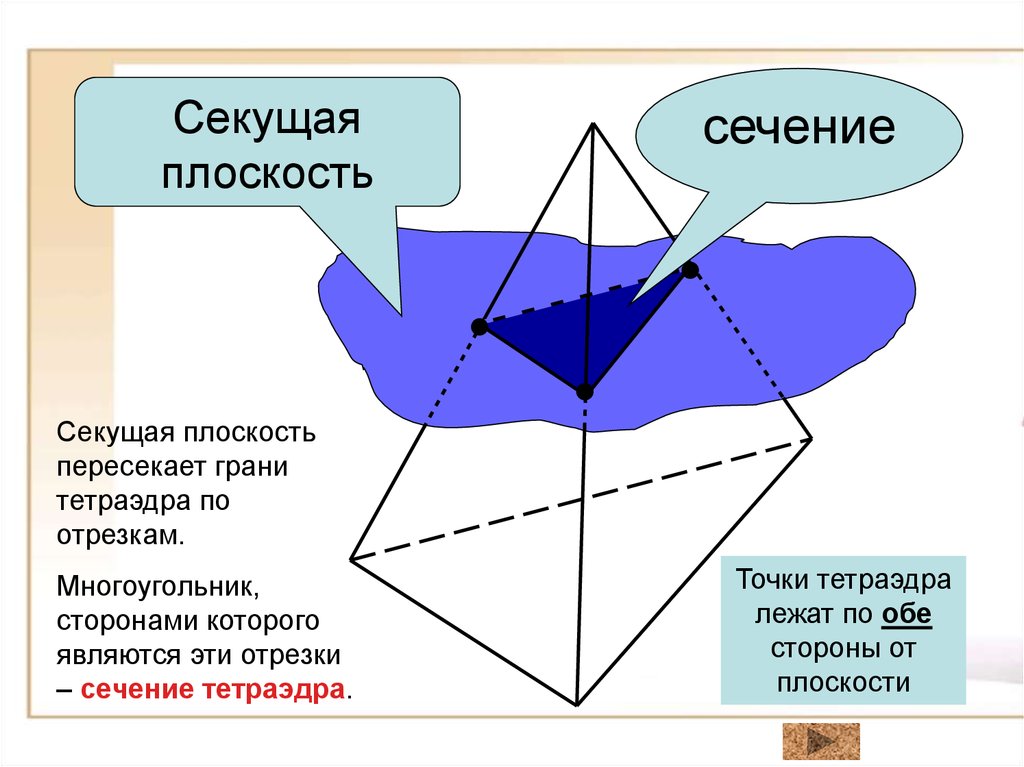
Секущая
плоскость
сечение
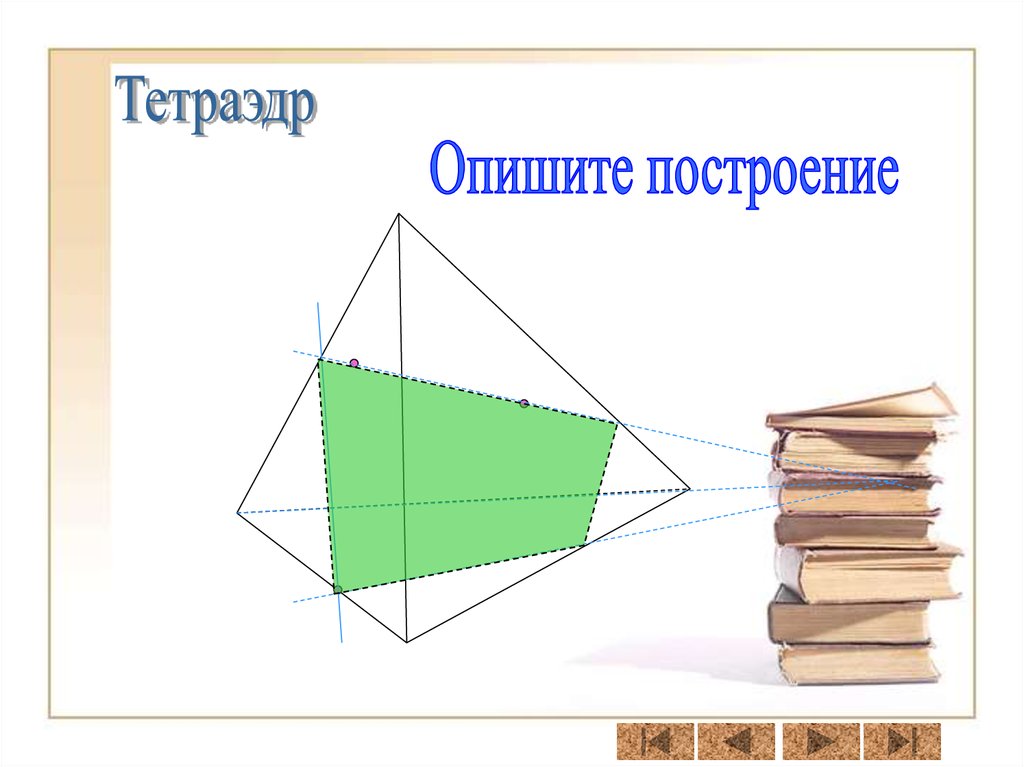
Секущая плоскость
пересекает грани
тетраэдра по
отрезкам.
Многоугольник,
сторонами которого
являются эти отрезки
– сечение тетраэдра.
Точки тетраэдра
лежат по обе
стороны от
плоскости

4.

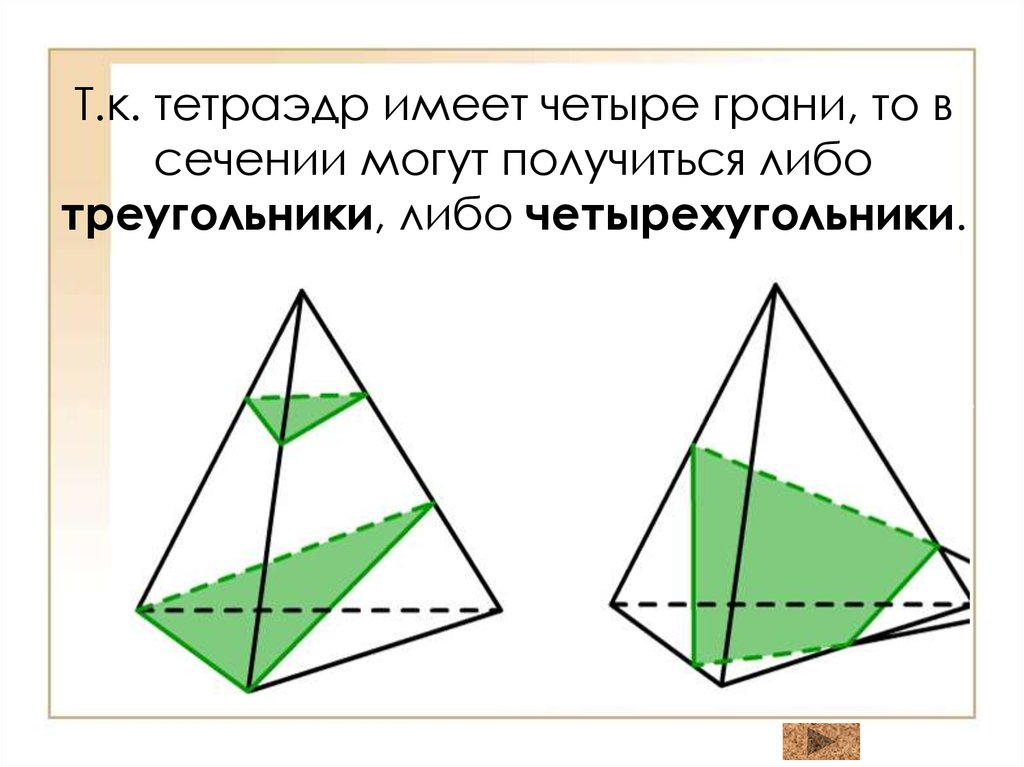
Т.к. тетраэдр имеет четыре грани, то в
сечении могут получиться либо
треугольники, либо четырехугольники.

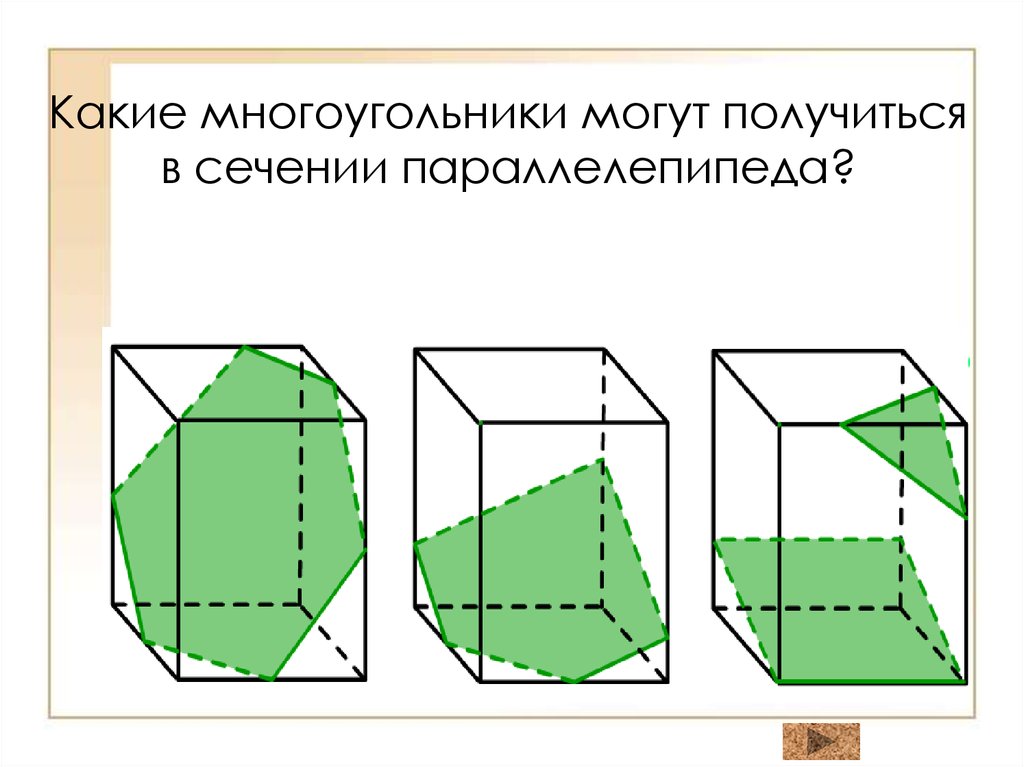
5. Какие многоугольники могут получиться в сечении параллелепипеда?

6.

ВАЖНО!
Для построения сечений ищем
отрезки, по которым секущая
плоскость пересекает каждую грань.
Можно соединять только точки,
которые лежат в одной плоскости.
Если секущая плоскость
пересекает противоположные грани,
то она пересекает их по
параллельным отрезкам.

7.

8.

9.

10.

11.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Решение 1 Решение 2
Решение 3
Решение 4
Решение 5 Решение 6
Решение 7
Решение 8
Решение 9 Решение 10 Решение 11 Решение 12
Решение 13Решение 14 Решение 15 Решение 16

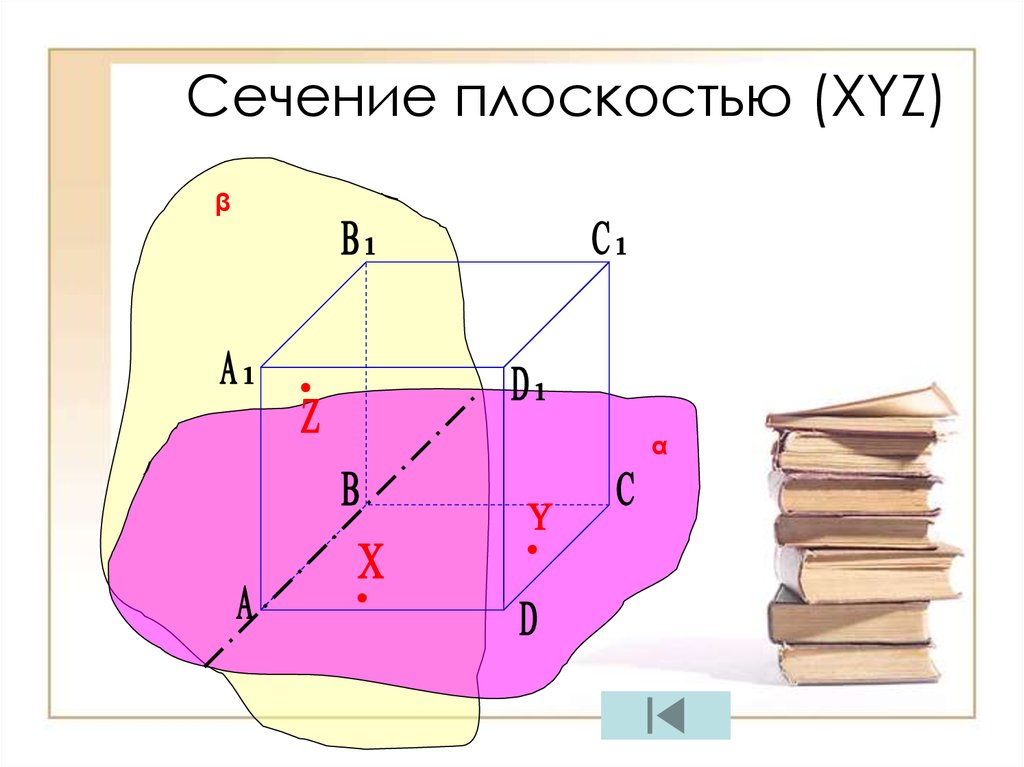
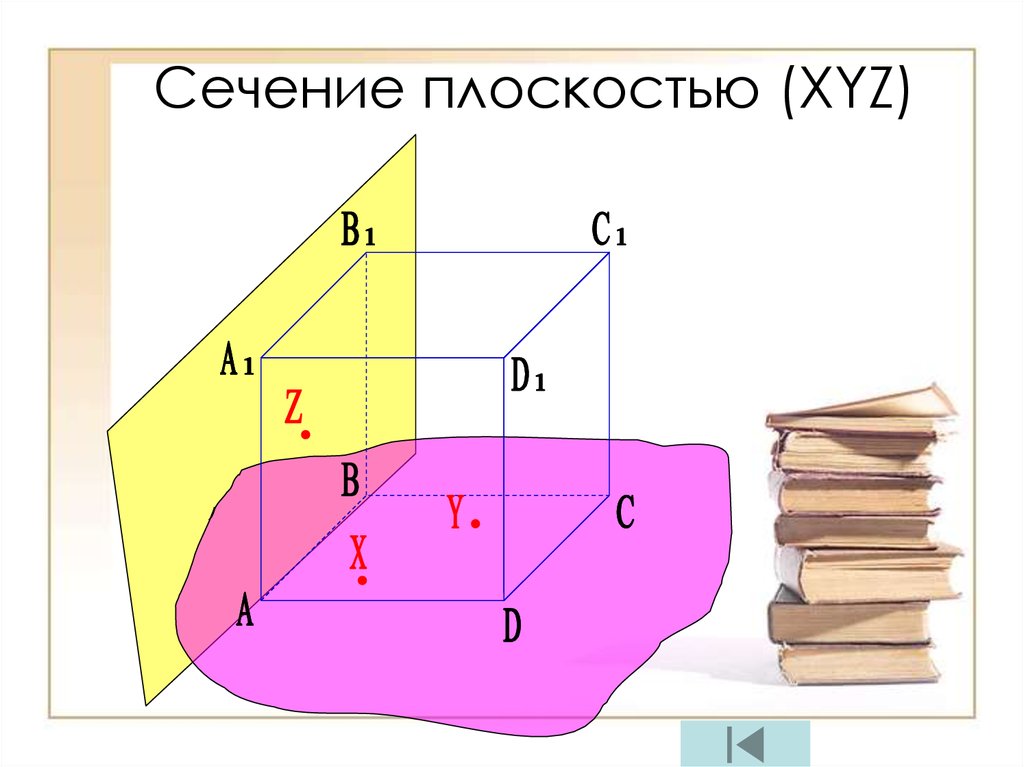
12. Сечение плоскостью (XYZ)

β
α

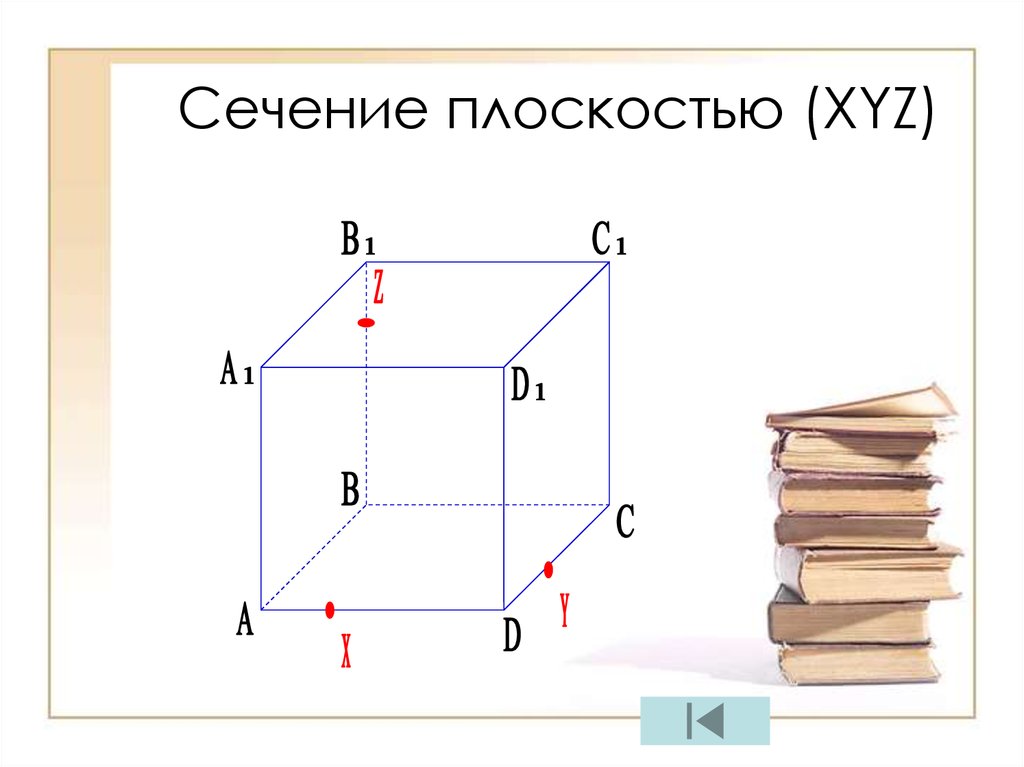
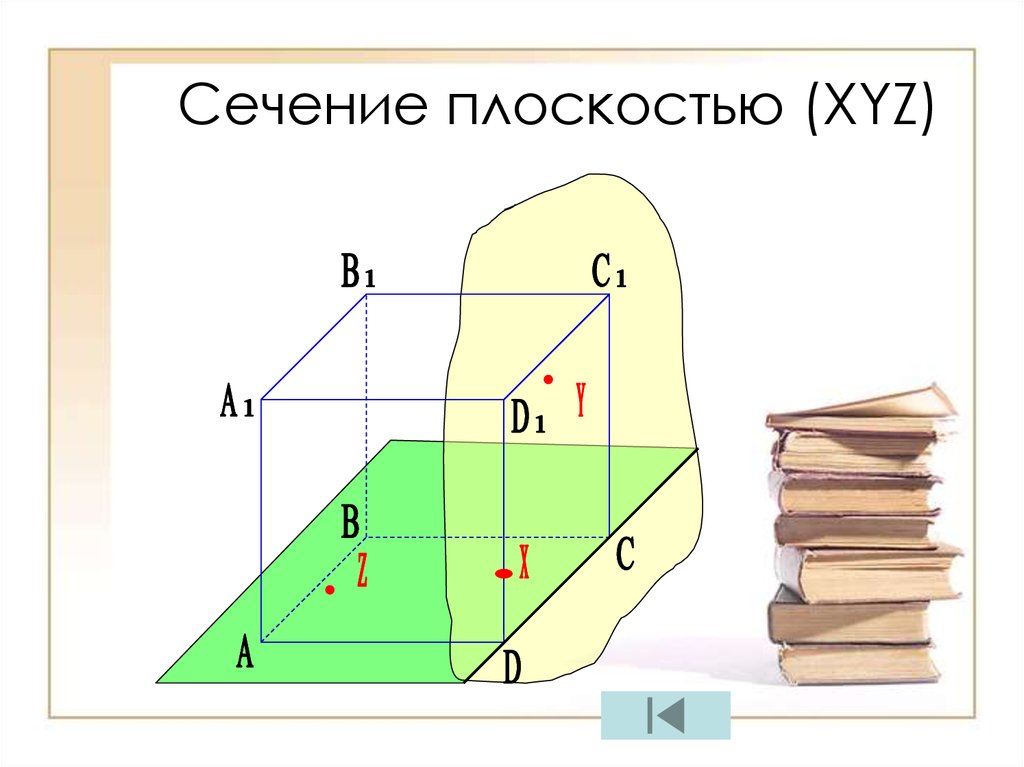
13. Сечение плоскостью (XYZ)

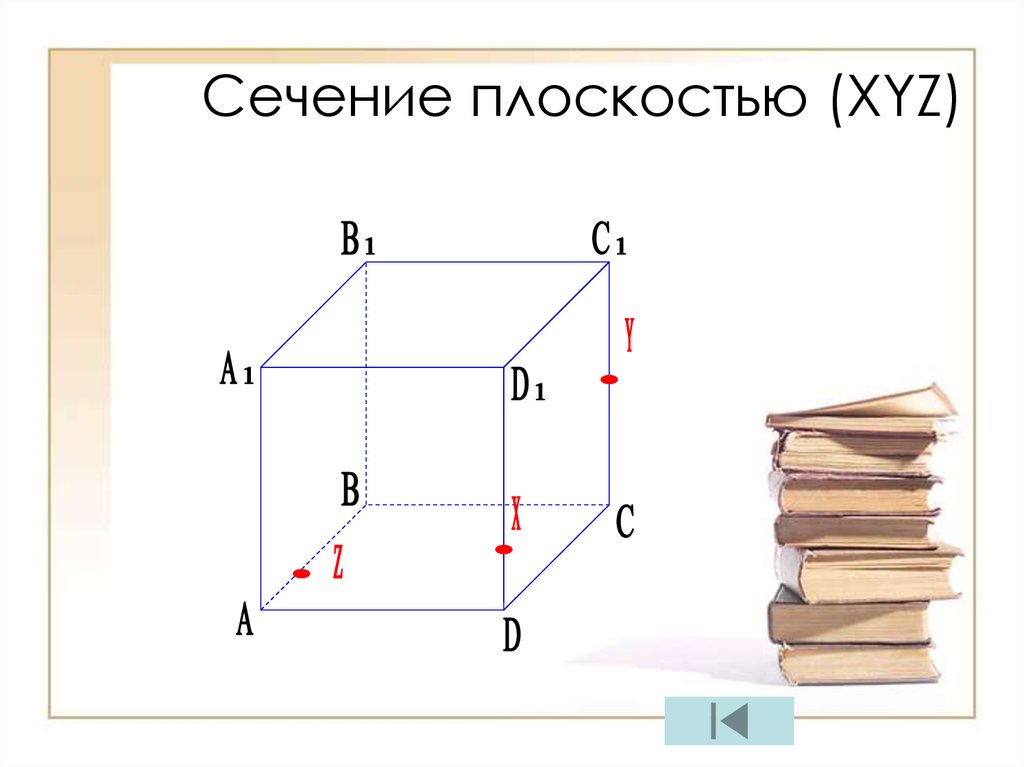
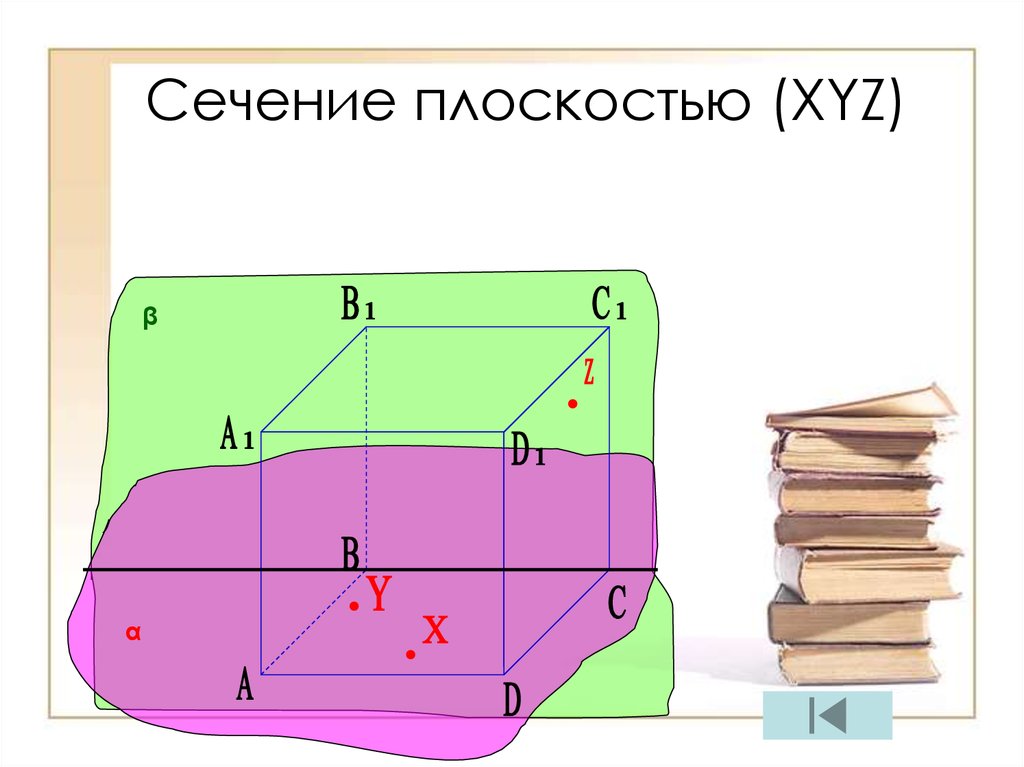
14. Сечение плоскостью (XYZ)

15. Сечение плоскостью (XYZ)

16. Сечение плоскостью (XYZ)

17. Сечение плоскостью (XYZ)

β
α

18.

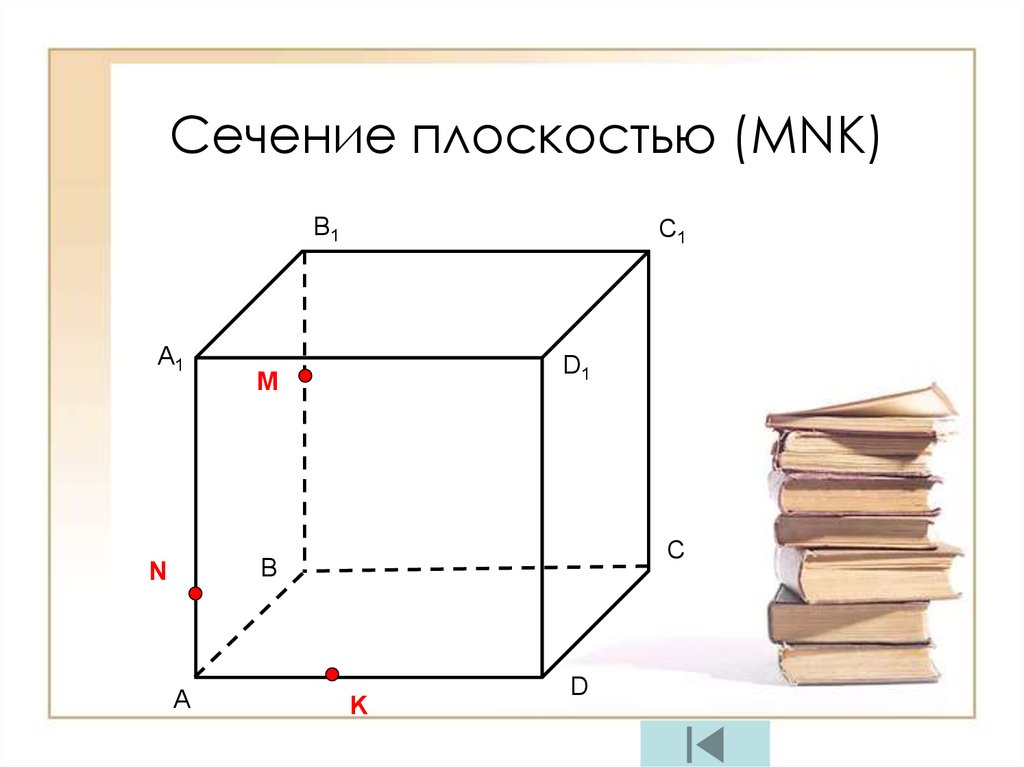
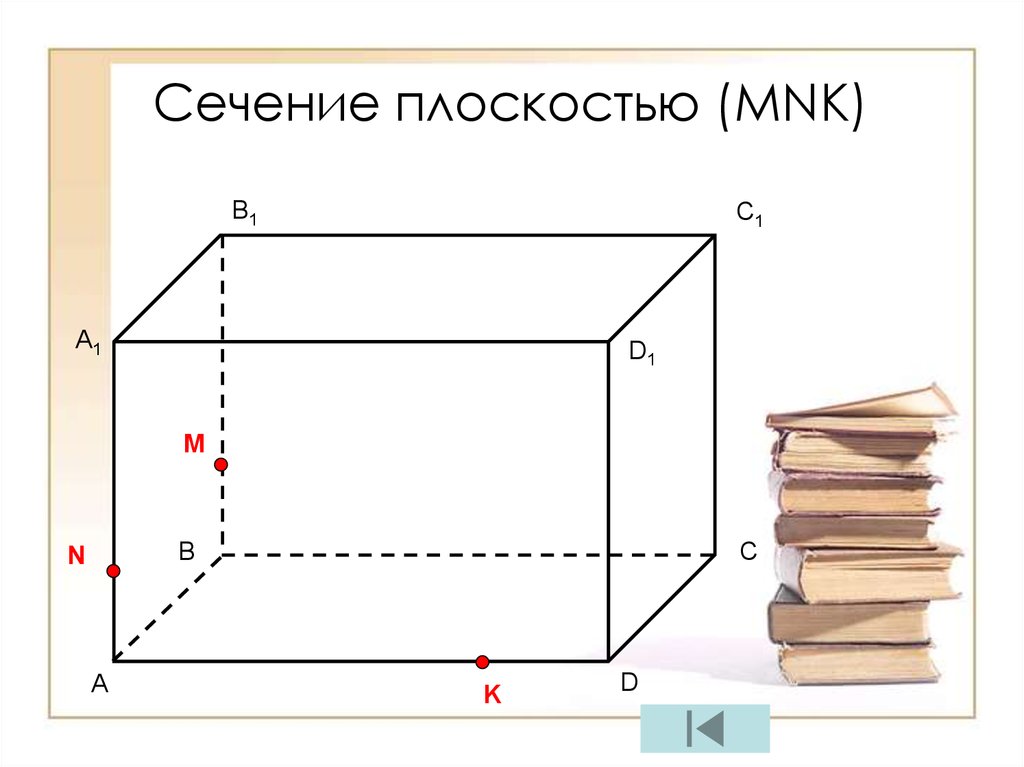
Сечение плоскостью (МNК)
B1
A1
C1
D1
M
C
B
N
A
K
D

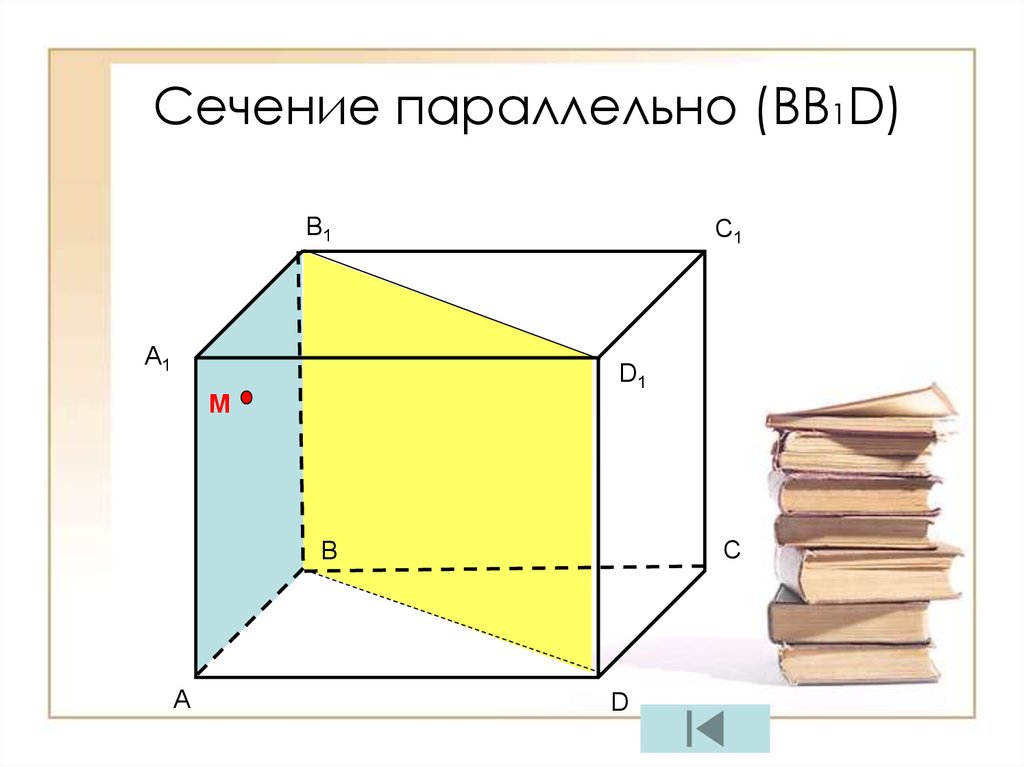
19. Сечение параллельно (ВВ1D)

B1
A1
C1
D1
M
C
B
A
D

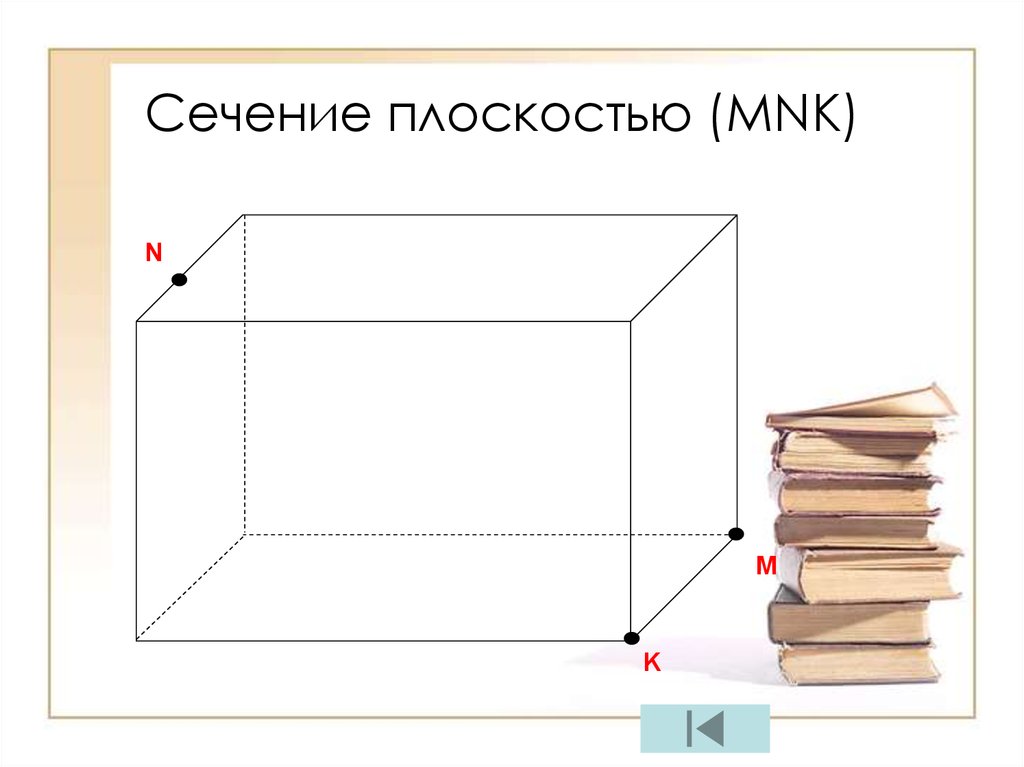
20.

Сечение плоскостью (МNК)
N
M
K

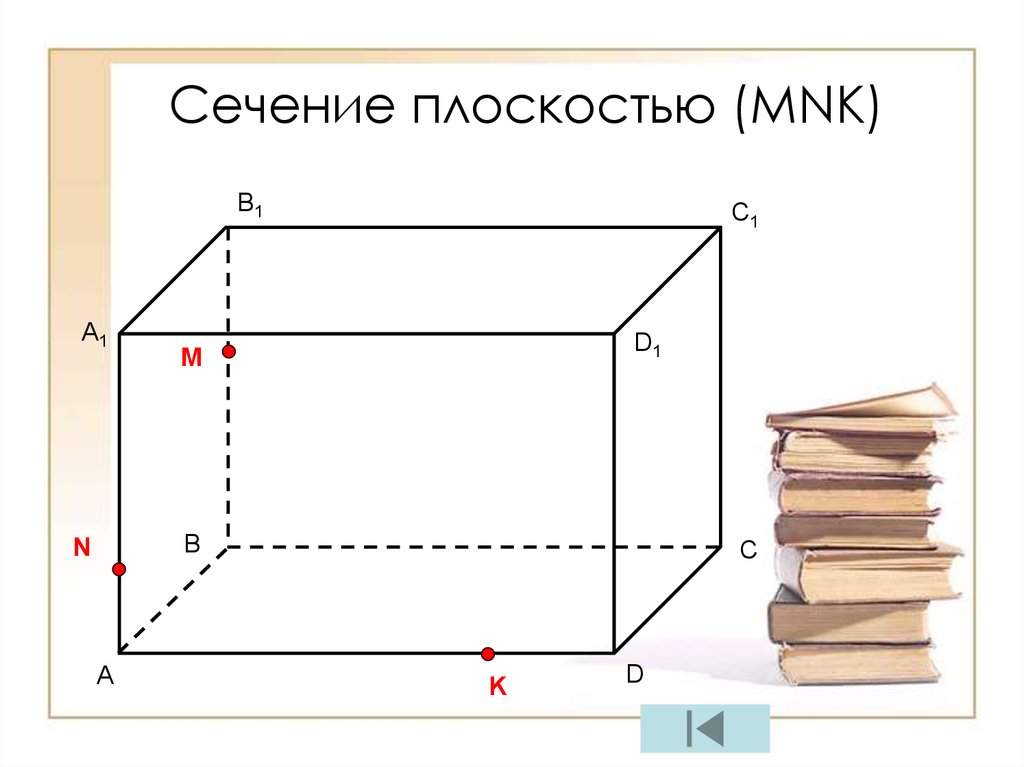
21.

Сечение плоскостью (МNК)
B1
A1
C1
D1
M
B
N
A
C
K
D

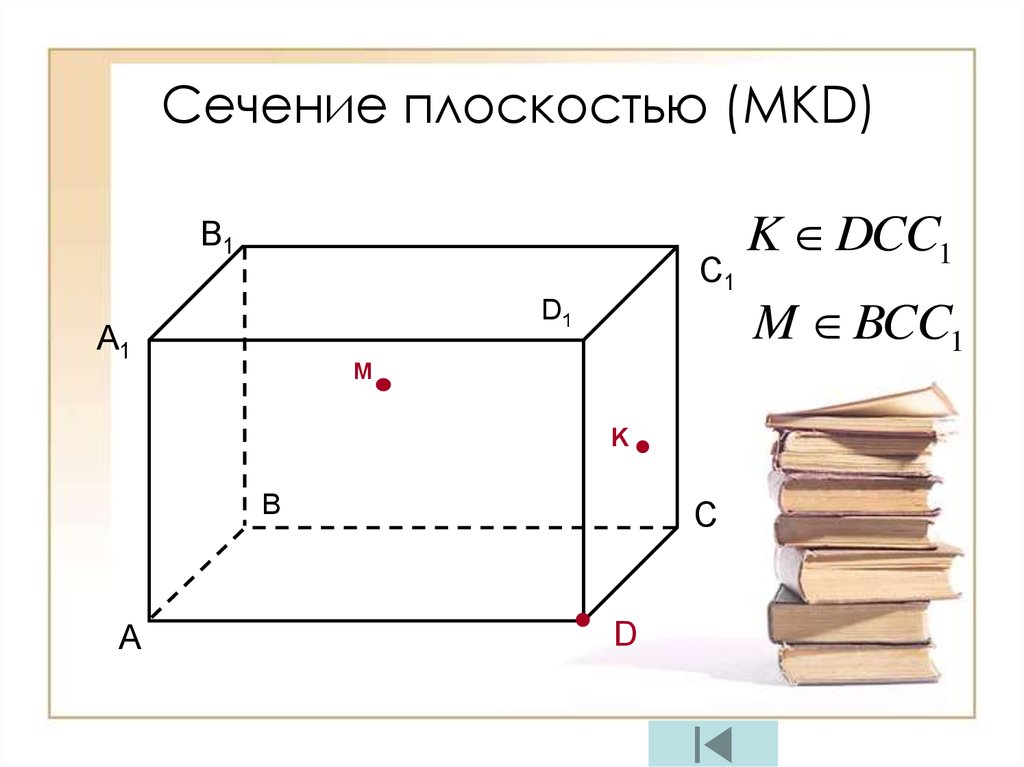
22.

Сечение плоскостью (МКD)
B1
C1
D1
A1
M
K
B
A
С
D
K DCC1
M BCC1

23.

Сечение плоскостью (МNК)
B1
C1
A1
D1
M
B
N
A
C
K
D

24.

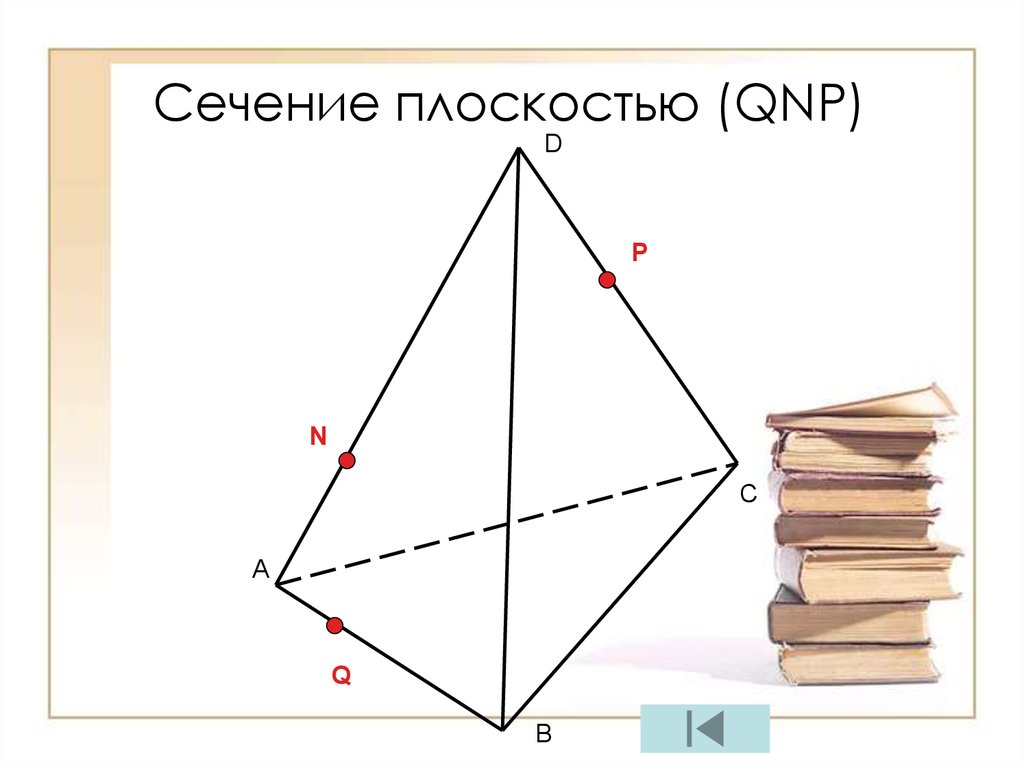
Сечение плоскостью (QNP)
D
P
N
С
А
Q
В

25.

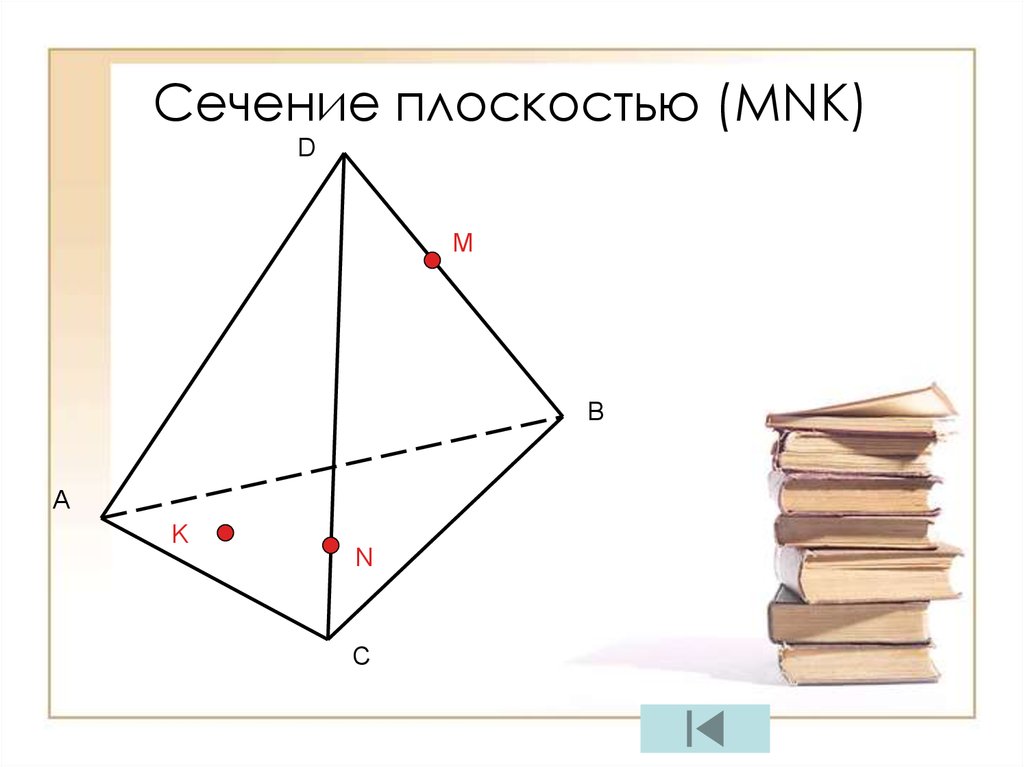
Сечение плоскостью (МNК)
D
M
B
A
K
N
C

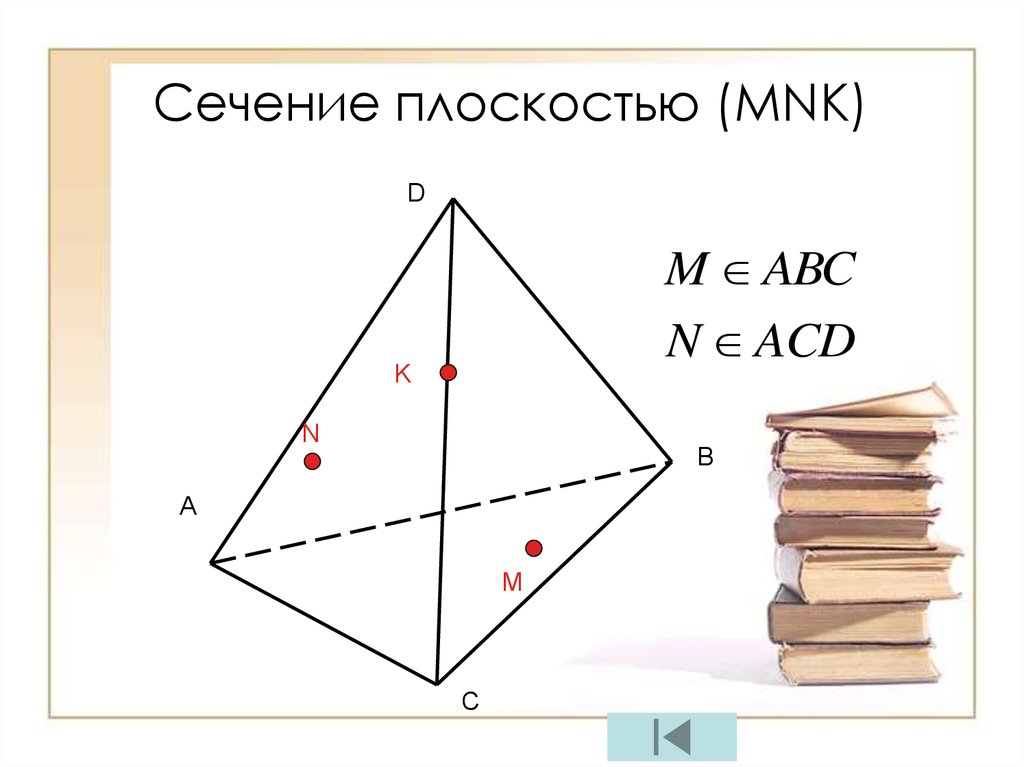
26.

Сечение плоскостью (МNК)
D
M ABC
N ACD
K
N
B
A
M
C

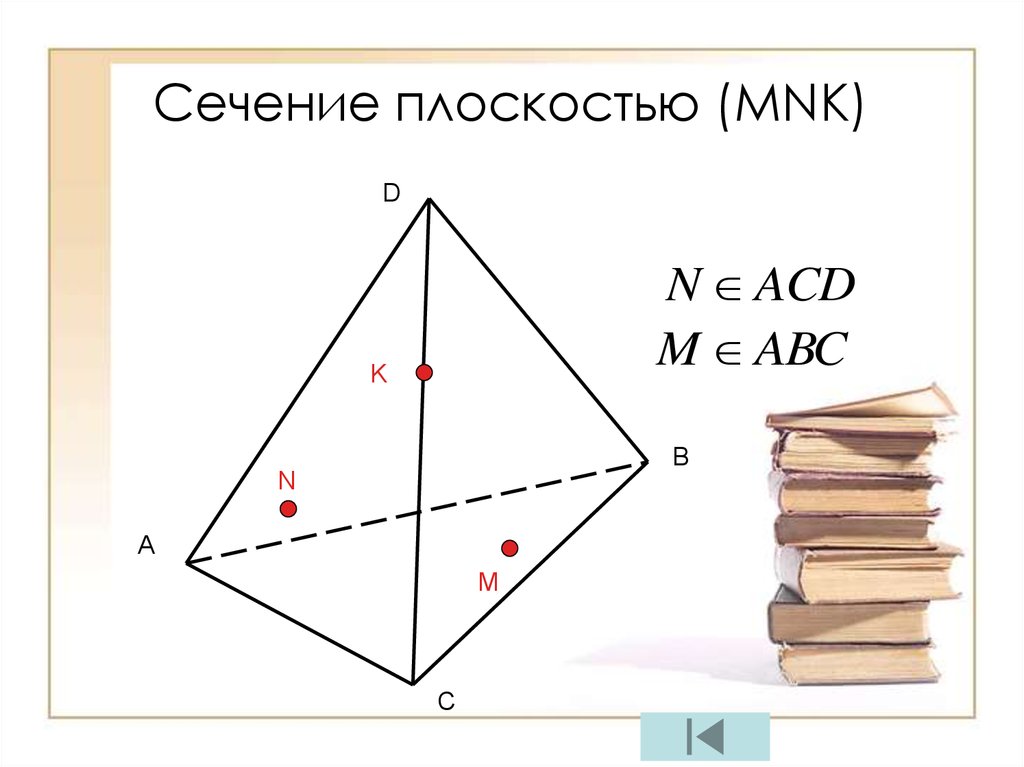
27.

Сечение плоскостью (МNК)
D
N ACD
M ABC
K
B
N
A
M
C