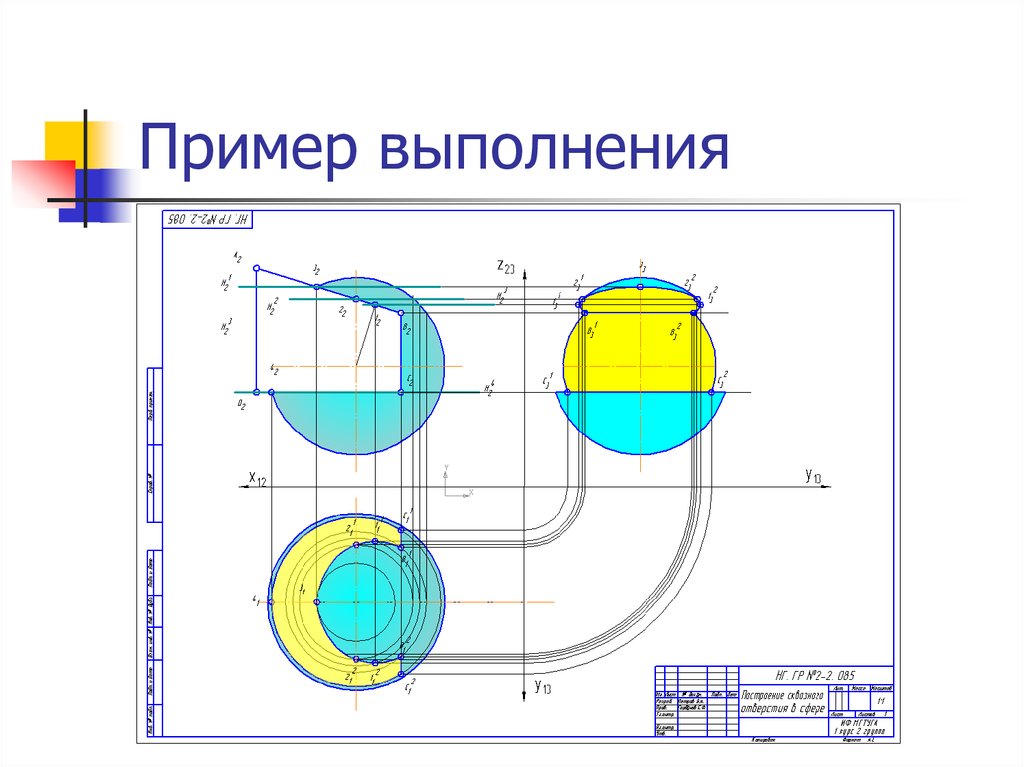
Построение сквозного отверстия в сфере

1. Контрольное домашнее задание №1

Задача №3 «Построение
сквозного отверстия в сфере»

2. Задание и выбор варианта

Построить горизонтальную и профильную
проекции сквозного четырехугольного отверстия
ABCD в сфере заданного диаметра R.
Номер задания выбирается по номеру зачетной
книжки. Предположим две последние цифры
номера зачетной книжки 85, следовательно,
координаты точек основания призматического
отверстия ABCD выбираем из пятого столбца, а
радиус сферы и координаты ее центра из восьмого
столбца (выбранные данные выделены в таблице
№1 заливкой).

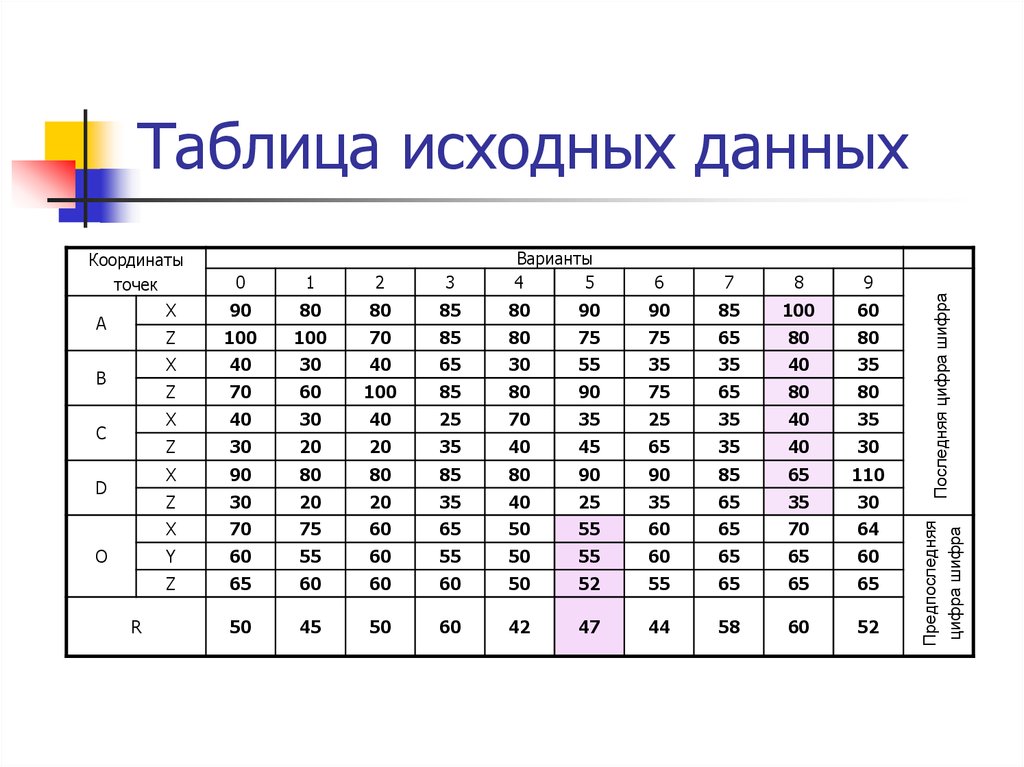
3. Таблица исходных данных

А
В
С
D
O
R
Варианты
4
5
0
1
2
3
6
7
8
9
X
90
80
80
85
80
90
90
85
100
60
Z
100
100
70
85
80
75
75
65
80
80
X
40
30
40
65
30
55
35
35
40
35
Z
70
60
100
85
80
90
75
65
80
80
X
40
30
40
25
70
35
25
35
40
35
Z
30
20
20
35
40
45
65
35
40
30
X
90
80
80
85
80
90
90
85
65
110
Z
30
20
20
35
40
25
35
65
35
30
X
70
75
60
65
50
55
60
65
70
64
Y
60
55
60
55
50
55
60
65
65
60
Z
65
60
60
60
50
52
55
65
65
65
50
45
50
60
42
47
44
58
60
52
Предпоследняя
цифра шифра
Координаты
точек
Последняя цифра шифра
Таблица исходных данных

4. Требования к оформлению задания

Задание выполняется в КОМПАС с распечаткой на цветном принтере. При
этом должны соблюдаться следующие условия:
Работа выполняется на листе чертежной бумаги формата А3 (297Х420) по
ГОСТ 2.301 – 68 г, лист располагается горизонтально, выполняется
основная надпись по ГОСТ 2.104 – 68 г (форма 1), линии на чертеже
выполняются согласно ГОСТ 2.303 – 68, надписи на чертеже выполняются
чертежным шрифтом по ГОСТ 2.304 – 81, тип А с наклоном. Исходные
данные заносятся в таблицу.
Видимые линии изображаются на чертеже сплошной основной линией,
невидимые штриховой;
Линии построения изображаются сплошной тонкой линией;
Искомые линии изображаются основной линией;
Поверхность сферы должна иметь сферическую заливку синего или
зеленого цвета. Поверхность призматического отверстия имеет плоскую
заливку желтого или оранжевого цвета. Интенсивность заливки
подбирается так, чтобы хорошо различались линии построения и
считывались обозначения точек.

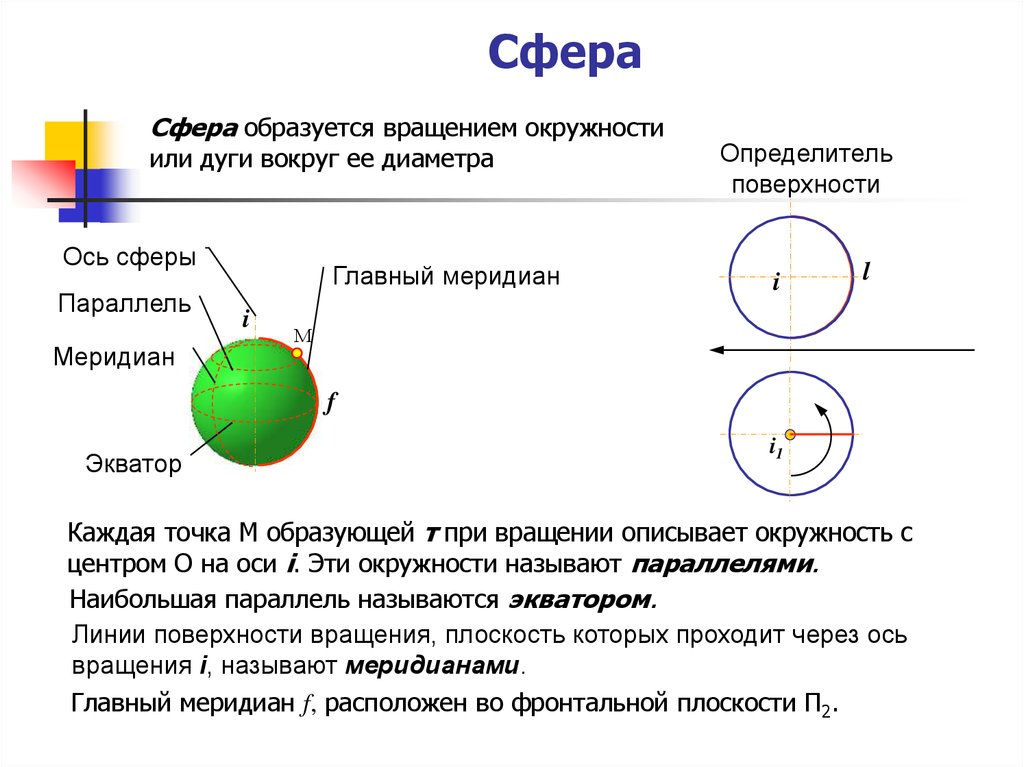
5. Сфера

Сфера образуется вращением окружности
или дуги вокруг ее диаметра
Ось сферы
Параллель
Меридиан
Главный меридиан
i
Определитель
поверхности
i
l
М
f
Экватор
i1
Каждая точка М образующей т при вращении описывает окружность с
центром О на оси i. Эти окружности называют параллелями.
Наибольшая параллель называются экватором.
Линии поверхности вращения, плоскость которых проходит через ось
вращения i, называют меридианами.
Главный меридиан f, расположен во фронтальной плоскости П2.

6. Сечения сферы плоскостью

Любая плоскость рассечет сферу по окружности. В зависимости от ее
положения относительно плоскостей проекции она проецируется в
окружность, эллипс или отрезок прямой.
- горизонтальная плоскость уровня ( П1).
Горизонтальная проекция сечения - окружность
2
2
- фронтально-проецирующая плоскость ( П2)
проходит через центр сферы. Горизонтальная проекция
сечения – эллипс оси которого пересекаются в центре
сферы.
2
x
2
d
900
- фронтально-проецирующая плоскость ( П2).
Горизонтальная проекция сечения - эллипс центр
которого расположен на перпендикуляре к
плоскости восстановленном из центра сферы.
- профильная плоскость уровня ( П3).
Горизонтальная проекция сечения – прямая
перпендикулярная оси эпюра

7. Построение горизонтальной проекции

Решаем задачу методом секущих горизонтальных плоскостей уровня.
А2
B2
12
900
z23 Грань АВ призматического отверстия задает
горизонтальную плоскость уровня 12 , которая
12
рассекает поверхность сферы по окружности
(проекции В11 и В21расположены на ней).
2
O2
D2
32
22
32
C2
22
2
X12
311
21
O1
D11
B11
11
B12
312
D12
y13
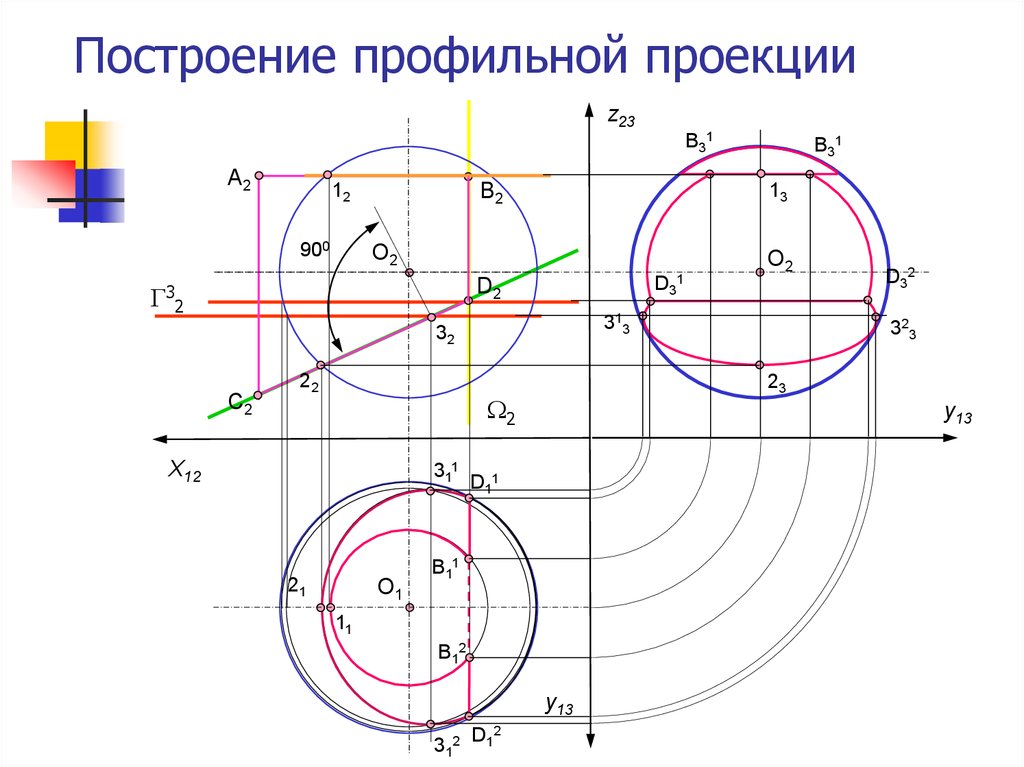
Грань BD задает профильную плоскость
уровня 2 и проецируется на П1 в линию.
Для определения положения проекций точек
D11 и D21 рассечем поверхность сферы
плоскостью уровня 22.
Грань DC задает фронтально-проецирующую
плоскость 2. Сечение проецируется на П1 в
виде эллипса.
Точка 2 определяет положение первой
вершины эллипса. Горизонтальная проекция 21
расположена на главном меридиане
Точка 3 определяет положение второй
вершины эллипса и его центра (ось эллипса
является фронтально-проецирующей прямой).
Для определения положения проекций точек
311 и 321 рассечем поверхность сферы
плоскостью уровня 32.

8. Построение профильной проекции

z23
B31
А2
B2
12
900
13
O2
D31
D2
32
22
311
21
O1
D11
11
B12
y13
D12
323
y13
B11
312
D32
23
2
X12
O2
313
32
C2
B31

9. Пример выполнения