Моделирование ВС. Обслуживание с ожиданием. (Тема 3.1.1)

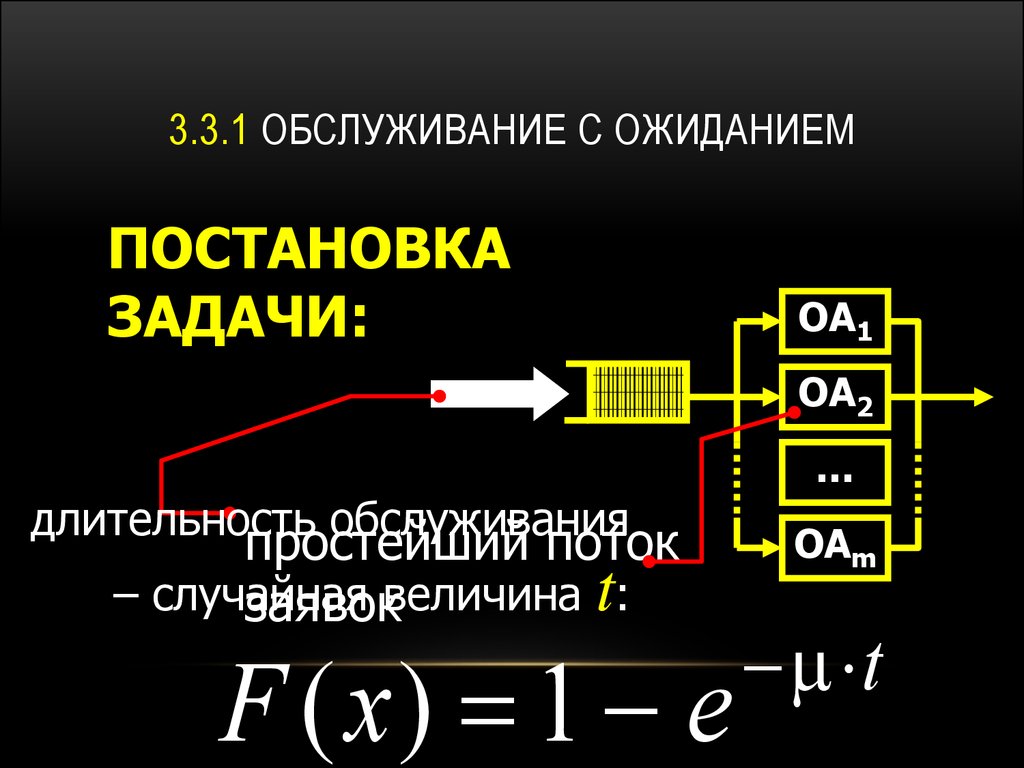
1. 3.3.1 ОБСЛУЖИВАНИЕ С ОЖИДАНИЕМ

ПОСТАНОВКА
ЗАДАЧИ:
ОА1
ОА2
длительность обслуживания
простейший поток
– случайная
заявоквеличина t:
F ( x) 1 e
…
ОАm
t

2. ПРИМЕР Исследование свойств экспоненциального распределения

ПРИМЕР ИССЛЕДОВАНИЕ СВОЙСТВ
ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Пусть Pa(t) – вероятность того, что
обслуживание, которое уже
продолжается время а, продлиться
еще не менее, чем время t.
a
0
t
t

3. Свойство экспоненциального распределения (продолжение)

СВОЙСТВО ЭКСПОНЕНЦИАЛЬНОГО
РАСПРЕДЕЛЕНИЯ (ПРОДОЛЖЕНИЕ)
Pa(t)
P0(a) = e- a
a
0
a+t
P0(a+t) =
t
- (a+t)
e
t

4. Свойство экспоненциального распределения (продолжение)

СВОЙСТВО ЭКСПОНЕНЦИАЛЬНОГО
РАСПРЕДЕЛЕНИЯ (ПРОДОЛЖЕНИЕ)
P0(a+t) = P0(a) Pa(t)
e- (a+t) = e- a Pa(t)
e- (a+t)
- t
Pa(t) =
=e
- a
e
не зависит от a

5. Распределение Эрланга (гамма-распределение с целочисленным параметром b)

РАСПРЕДЕЛЕНИЕ ЭРЛАНГА
(ГАММА-РАСПРЕДЕЛЕНИЕ С ЦЕЛОЧИСЛЕННЫМ
ПАРАМЕТРОМ B)
Плотность распределения:
0 , при t 0,
b1
f ( t ) ( t )
t
e
при
t
0,
(b-1)!
где
b – целое положительное число

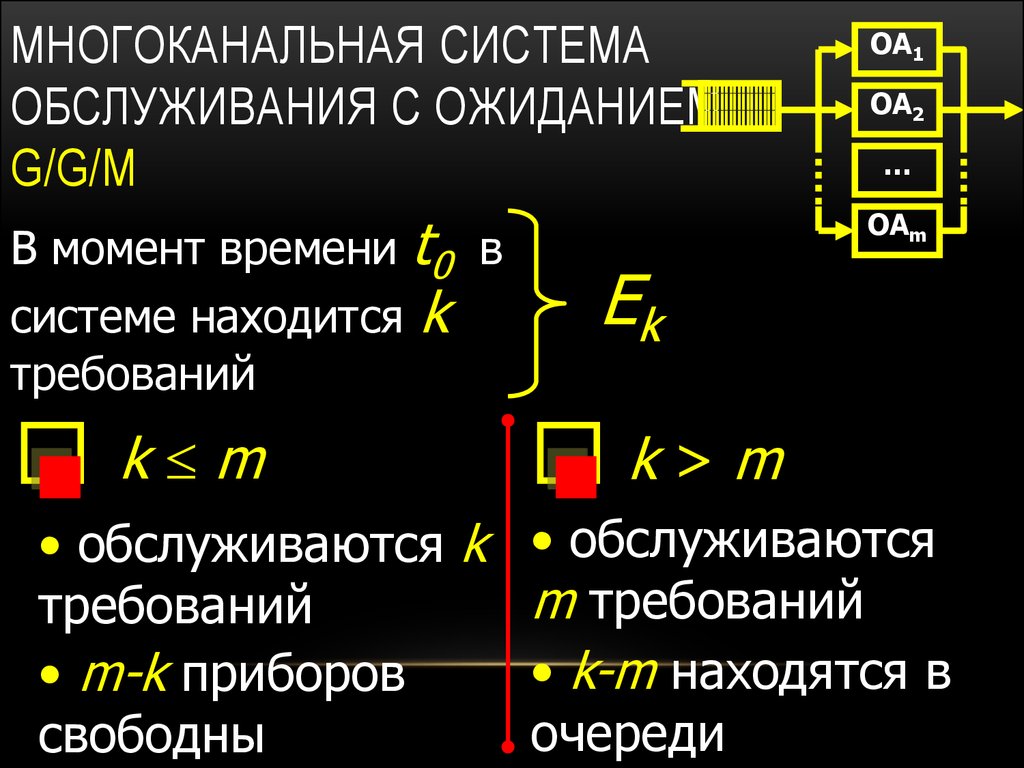
6. Многоканальная система обслуживания с ожиданием G/G/m

МНОГОКАНАЛЬНАЯ СИСТЕМА
ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ
G/G/M
ОА1
В момент времени t0 в
системе находится k
требований
ОАm
k m
ОА2
…
Ek
k>m
• обслуживаются k • обслуживаются
m требований
требований
• k-m находятся в
• m-k приборов
очереди
свободны

7. Параметры, определяющие обслуживание после t0

ПАРАМЕТРЫ, ОПРЕДЕЛЯЮЩИЕ
ОБСЛУЖИВАНИЕ ПОСЛЕ T0
моменты поступления новых заявок
длительность обслуживания заявок,
поступивших после t0
моменты окончания обслуживаний,
производящихся в момент времени t0
не зависят в вероятностном смысле от
того, как происходило обслуживание до
момента времени t0

8. Случайный процесс Маркова

СЛУЧАЙНЫЙ
ПРОЦЕСС МАРКОВА
Случайный процесс, для которого
будущее развитие зависит только
от достигнутого в данный момент
состояния и не зависит от того, как
происходило развитие в прошлом
Аналитическое моделирование СМО
применимо только к Марковским
процессам и системам

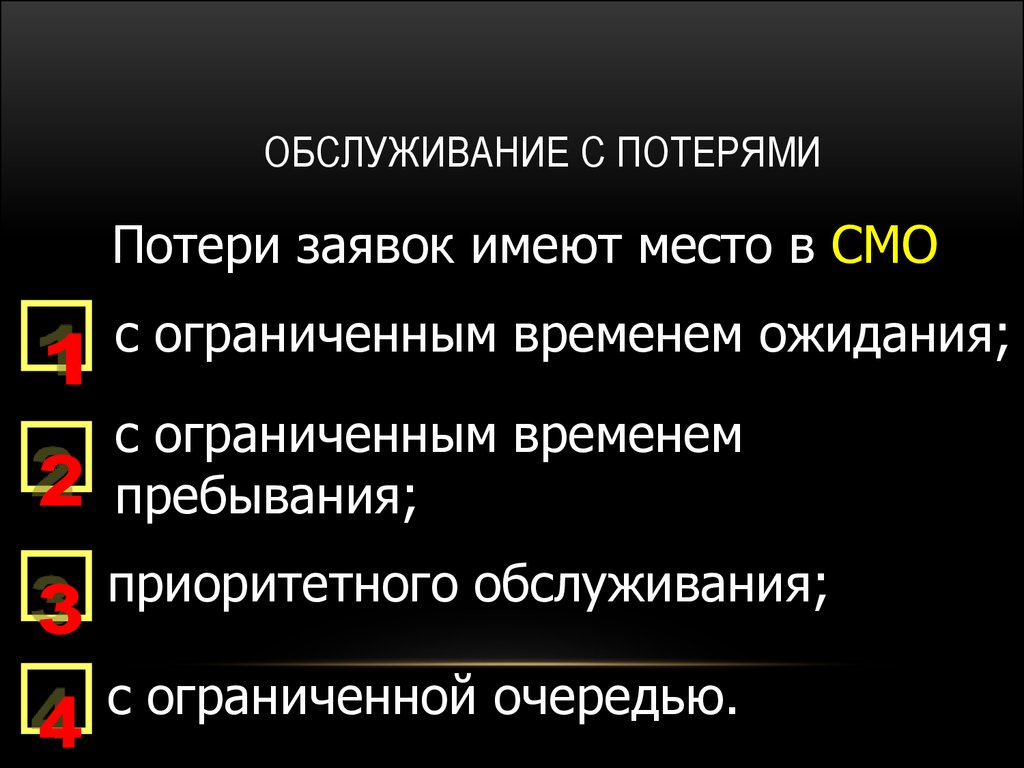
9. ОБСЛУЖИВАНИЕ С ПОТЕРЯМИ

Потери заявок имеют место в СМО
с ограниченным временем ожидания;
с ограниченным временем
пребывания;
приоритетного обслуживания;
с ограниченной очередью.

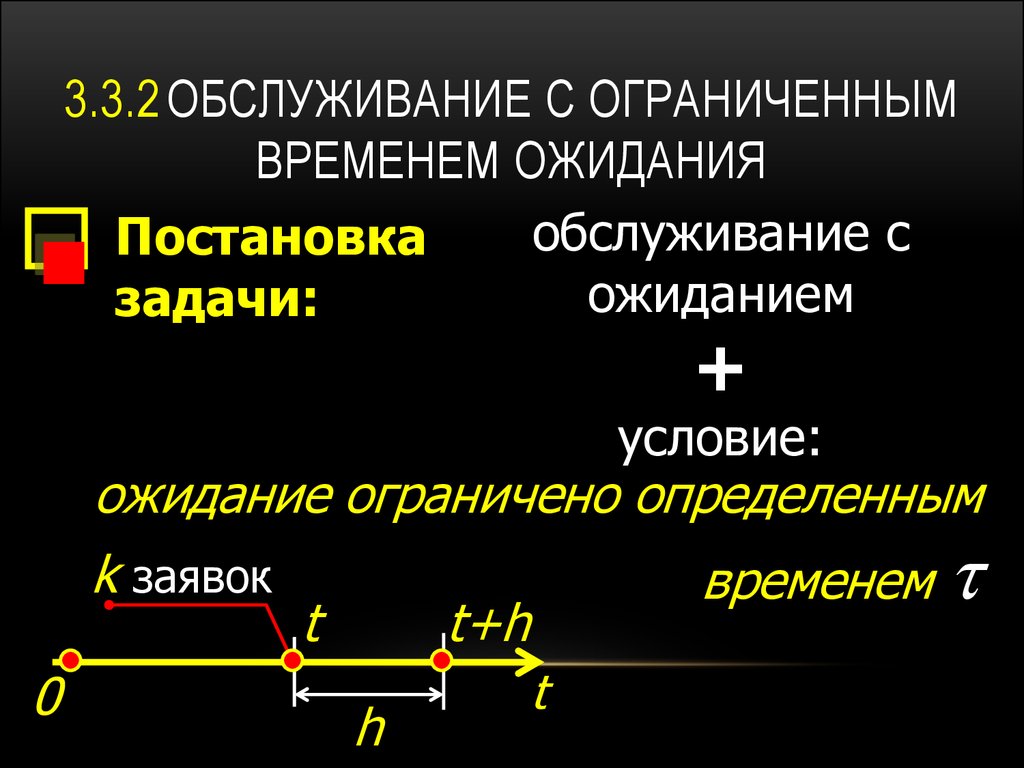
10. 3.3.2 ОБСЛУЖИВАНИЕ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ

обслуживание с
Постановка
ожиданием
задачи:
+
условие:
ожидание ограничено определенным
k заявок
временем
t
t+h
0
h
t

11. m-мерный случайный процесс (t):

M-МЕРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС (T):
(t)={ 1(t), 2(t)… m(t) }
где
i(t) – время, которое должно
протечь от момента t до
освобождения прибора с номером
от обслуживания заявок,
поступивших ранее t
i

12.

Если в момент времени t :
• аппарат с номером i свободен
и
• в системе нет заявок,
ожидающих обслуживания
i(t)=0
Заявка, поступившая в момент t,
выбирает прибор с номером i если:
i ( t ) min k ( t )
k

13.

Пусть на i-й аппарат, свободный
от обслуживания в момент
времени t=0
• заявки поступают в моменты
времени ti1 , ti2…
• необходимые для их
обслуживания длительности
времени равны соответственно
i1 , i2…

14.

i(t)
i3
i1
i4
отказ
ti1 ti2
ti3
ti4
i(ti2) >
t

15. 3.3.3 ОБСЛУЖИВАНИЕ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ

обслуживание с
Постановка
ожиданием
задачи:
+
условие:
пребывание заявки в системе
ограничено определенным временем

16.

tожидания + tобслуживания <
заявка обслужена полностью
tожидания <
tожидания + tобслуживания >
заявка потеряна с незавершенным
обслуживанием
tожидания >
чистая потеря (без затраты времени
на обслуживание)

17. ПРИМЕР Невозможность чистых потерь при дисциплине обслуживания FIFO

ПРИМЕР НЕВОЗМОЖНОСТЬ ЧИСТЫХ ПОТЕРЬ ПРИ
ДИСЦИПЛИНЕ ОБСЛУЖИВАНИЯ FIFO
Ординарный поток
раздельное поступление заявок в СМО
первая заявка
первая заявка покидает СМО
покидает
СМОобслуживание
начинается
второй заявки
t1
t1+
t2-t1 >
<
t2 t1+
вторая заявка
покидает СМО
t2+
t

18. m-мерный случайный процесс (t):

M-МЕРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС (T):
(t)={ 1(t), 2(t)… m(t) }
Ограничение:
i(t)

19.

Пусть на i-й аппарат, свободный
от обслуживания в момент
времени t=0
• заявки поступают в моменты
времени ti1 , ti2…
• необходимые для их
обслуживания длительности
времени равны соответственно
i1 , i2…

20.

До момента времени ti1
аппарат свободен от
обслуживания:
i(t) = 0
В момент времени ti1 при
поступлении заявки i(t) совершает
скачек, причем:
• если i(ti1) + i1
, то
i(ti1+0)= i(ti1)+ i1
• если i(ti1) + i1 > , то
i(ti1+0)=

21.

i(t)
tн.о2
i2
i1
i3
ti1
ti2
ti3 t2out
i(ti2)+ i2 >
i(ti2+0) =
t

22. 3.3.4 МОДЕЛИ ПРИОРИТЕТНОГО ОБСЛУЖИВАНИЯ

Постановка
задачи:
Абсолютный приоритет с
продолжением незавершенного
обслуживания
Абсолютный приоритет с потерей
незавершенного обслуживания
Абсолютный приоритет с
возобнавлением незавершенного
обслуживания

23. Приоритетное обслуживание

ПРИОРИТЕТНОЕ ОБСЛУЖИВАНИЕ
Заявки:
Первого типа
(приоритет)
• обслуживаются
независимо от
требований второго
типа
• аналитическая
модель обслуживания
с ожиданием
Второго
типа
• обслуживание
заявок первого типа
эквивалентно отказу
ОА
• математический
аппарат
моделирования СМО
с ненадежным
прибором