Перпендикулярные прямые

1.

ПЕРПЕНДИКУЛЯРНЫЕ
ПРЯМЫЕ
Игорь Жаборовский © 2011
UROKIMATEMATIKI.RU

2.

B
С
2
1
3
4
A
D
ВЕЛИЧИНА ОСТРОГО УГЛА-УГОЛ МЕЖДУ ПРЯМЫМИ

3.

B
1
С
A
D
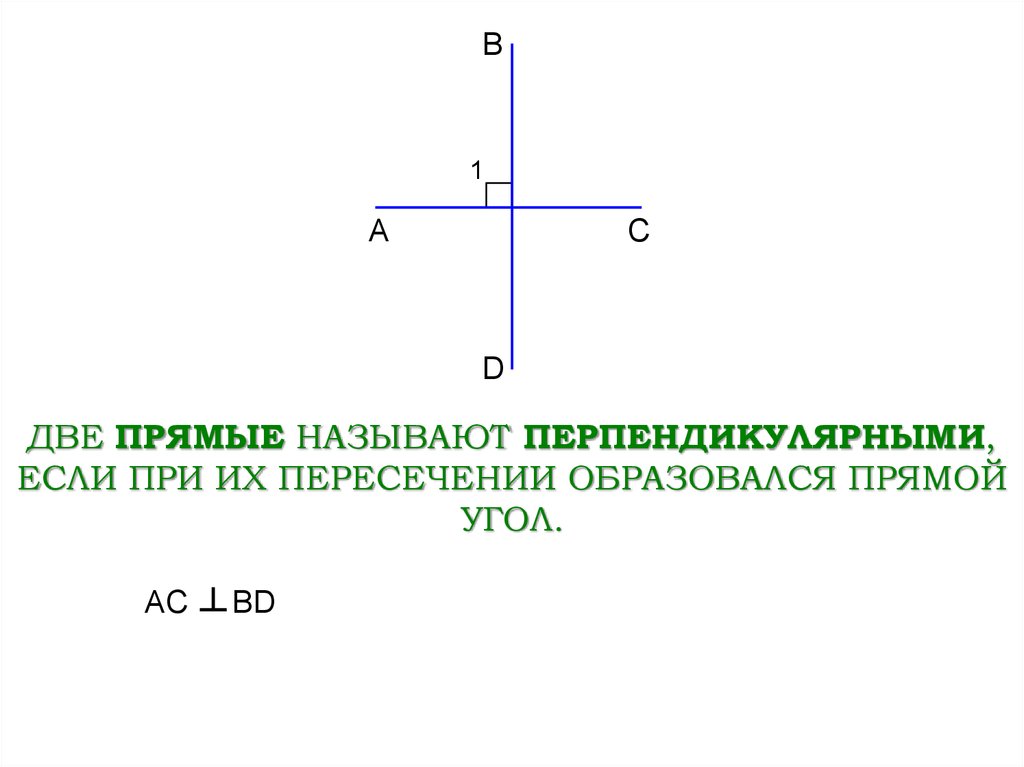
ДВЕ ПРЯМЫЕ НАЗЫВАЮТ ПЕРПЕНДИКУЛЯРНЫМИ,
ЕСЛИ ПРИ ИХ ПЕРЕСЕЧЕНИИ ОБРАЗОВАЛСЯ ПРЯМОЙ
УГОЛ.
AC ┴ BD

4.

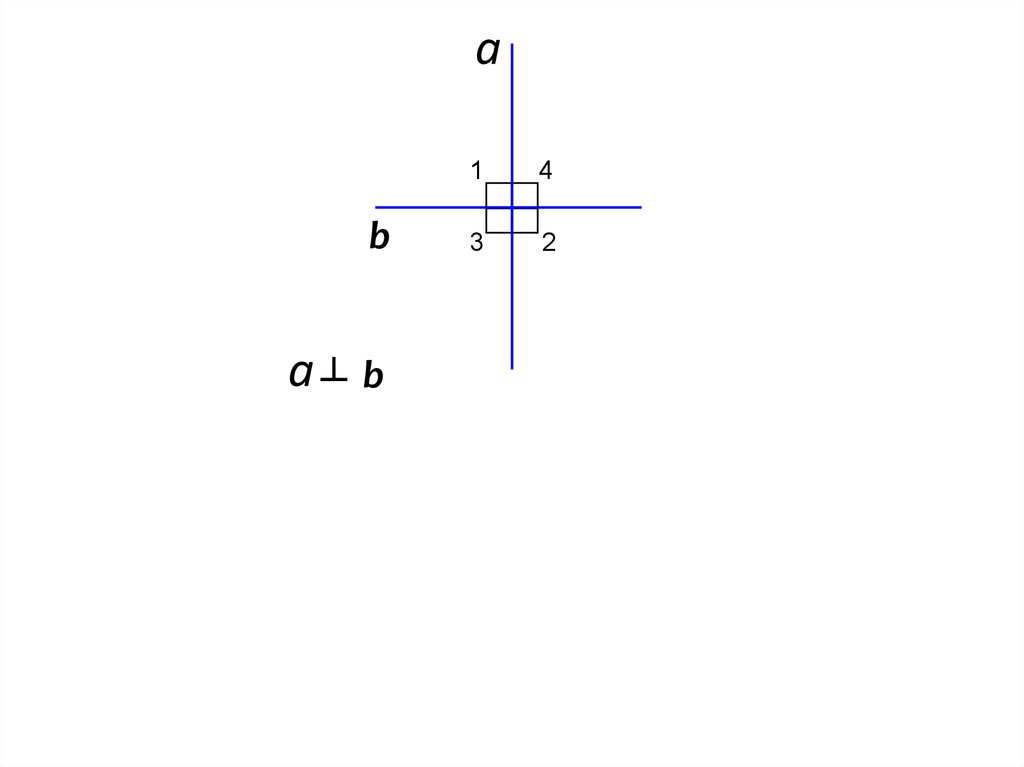
а
b
а┴
b
1
4
3
2

5.

B
1
A 1
С
1
A
С
С
A
D
B
B
D
D
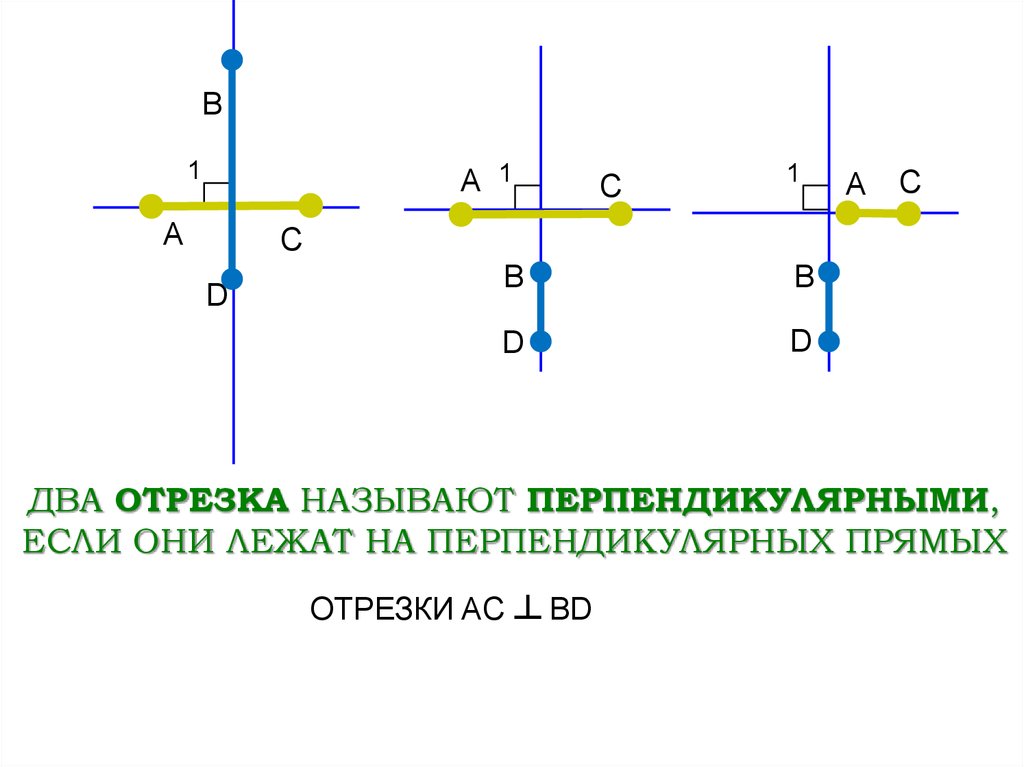
ДВА ОТРЕЗКА НАЗЫВАЮТ ПЕРПЕНДИКУЛЯРНЫМИ,
ЕСЛИ ОНИ ЛЕЖАТ НА ПЕРПЕНДИКУЛЯРНЫХ ПРЯМЫХ
ОТРЕЗКИ AC ┴ BD

6.

B
1
A 1
С
1
A
С
С
A
D
B
B
D
D
ДВА ОТРЕЗКА(ЛУЧА) НАЗЫВАЮТ
ПЕРПЕНДИКУЛЯРНЫМИ, ЕСЛИ ОНИ ЛЕЖАТ НА
ПЕРПЕНДИКУЛЯРНЫХ ПРЯМЫХ

7.

А
а
B
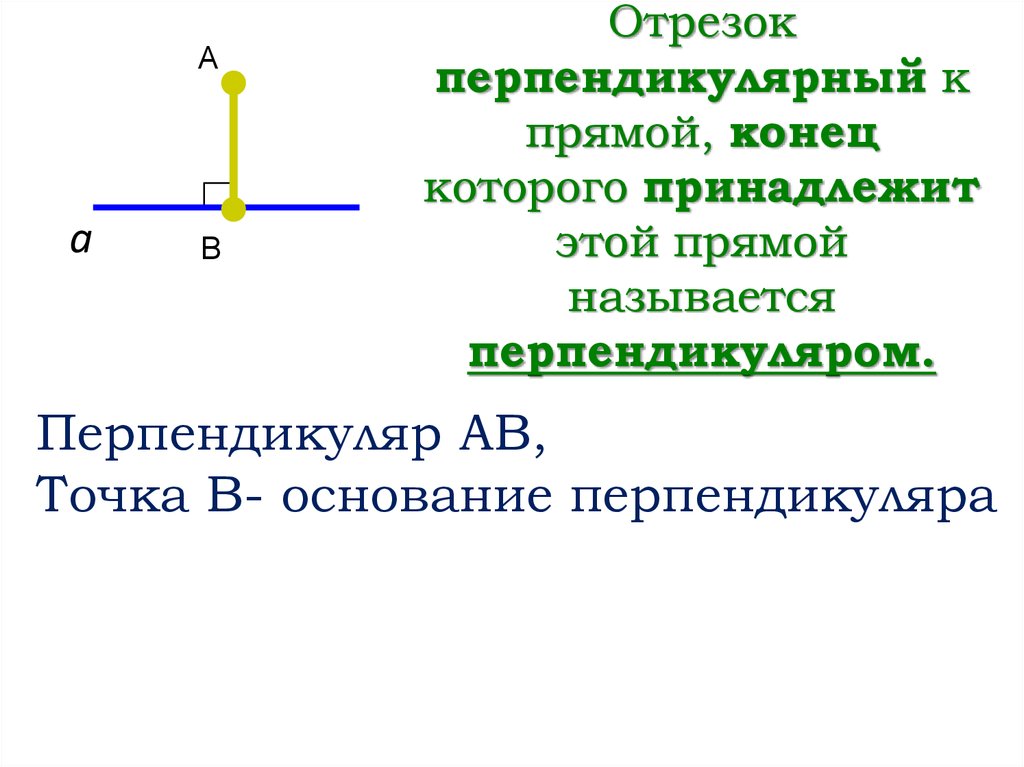
Отрезок
перпендикулярный к
прямой, конец
которого принадлежит
этой прямой
называется
перпендикуляром.
Перпендикуляр АВ,
Точка В- основание перпендикуляра

8.

А
а
А
а
B
B
А
А
а
B
а
B

9.

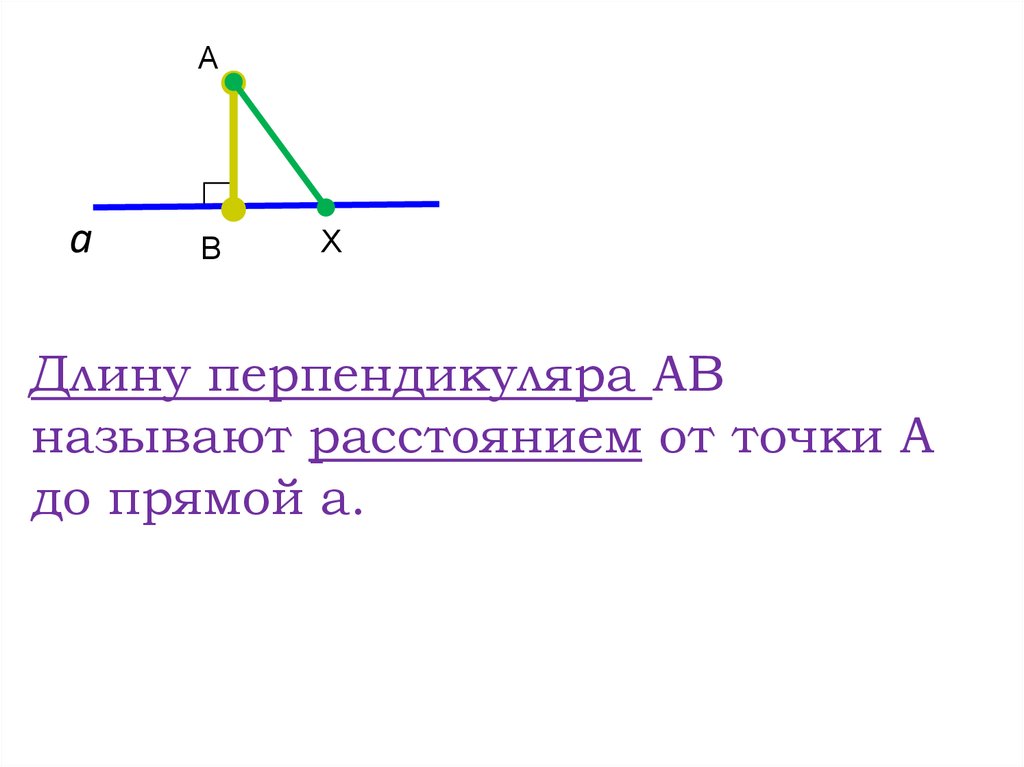
А
а
B
Х
Перпендикуляр АВ,
Точка В- основание перпендикуляра
Наклонная АХ

10.

А
а
B
Х
Длину перпендикуляра АВ
называют расстоянием от точки А
до прямой а.

11.

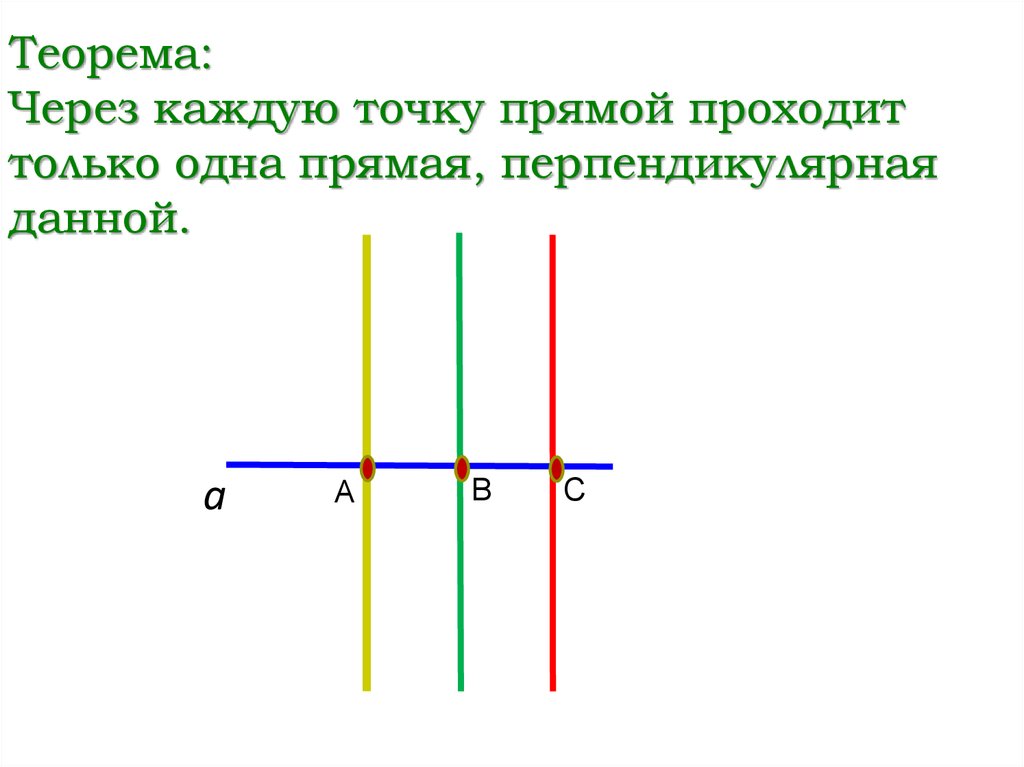
Теорема:
Через каждую точку прямой проходит
только одна прямая, перпендикулярная
данной.
а
А
B
С

12.

В
А
Игорь Жаборовский © 2011
О
UROKIMATEMATIKI.RU

13.

Теорема:
Через каждую точку прямой проходит
только одна прямая, перпендикулярная
данной.
С
Дано:
Прямая АВ
Точка М є АВ
МС ┴ АВ
B
М
А
Доказать:
прямая МС единственная

14.

С
D
А
М
B
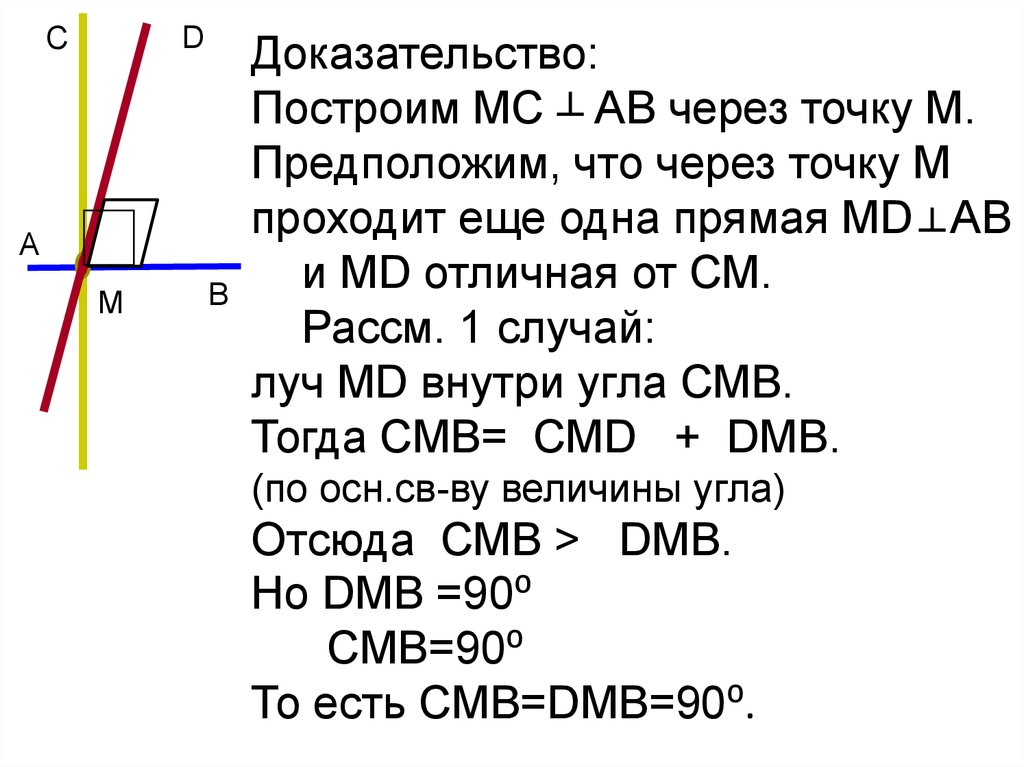
Доказательство:
Построим МС ┴ АВ через точку М.
Предположим, что через точку М
проходит еще одна прямая MD ┴ АВ
и MD отличная от СМ.
Рассм. 1 случай:
луч MD внутри угла СМВ.
Тогда СМВ= СМD + DMB.
(по осн.св-ву величины угла)
Отсюда СМВ > DMB.
Но DMB =90⁰
СМВ=90⁰
То есть CMB=DMB=90⁰.

15.

Но DMB =90⁰
СМВ=90⁰
То есть CMB=DMB=90⁰.
(угол СМВ не может быть больше угла DMB)
Следовательно, наше предположение
неверно. СМ –единственная.
(о существовании второй перпендикулярной
прямой проходящей через данную точку)

16.

С
D
Рассм. 2 случай:
луч MС внутри угла DМВ.
Тогда DМВ= СМD + CMB.
А
(по осн.св-ву величины угла)
М
B
Отсюда СМВ < DMB.
Но DMB =90⁰
СМВ=90⁰
То есть CMB=DMB=90⁰.

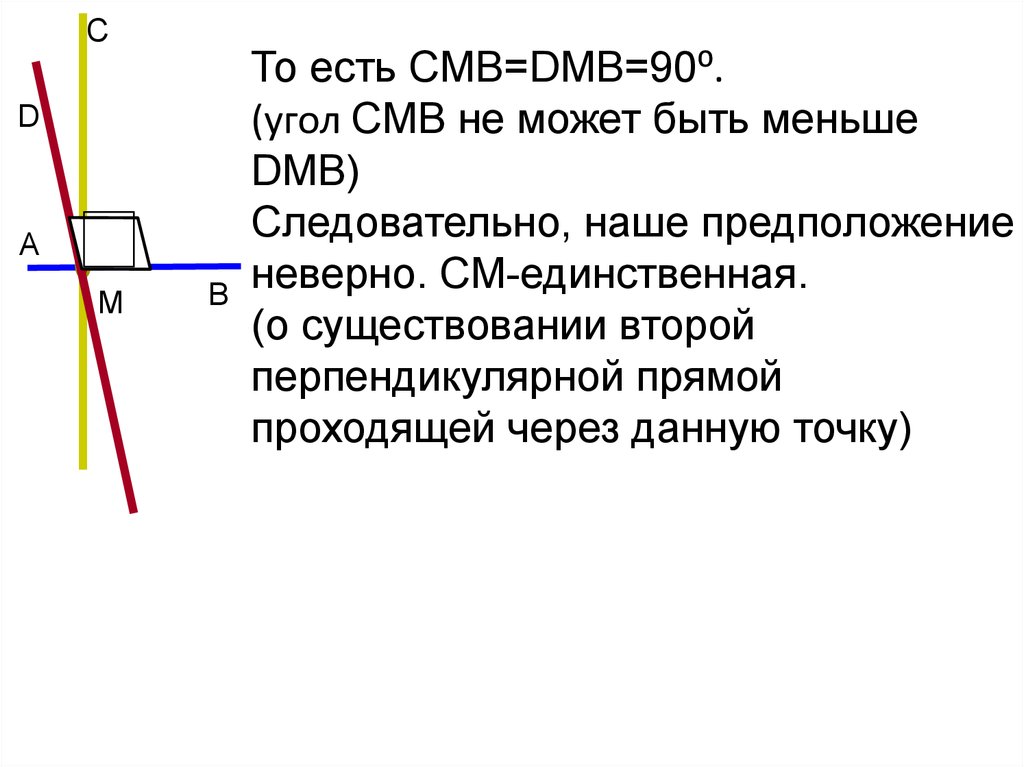
17.

С
D
А
М
B
То есть CMB=DMB=90⁰.
(угол СМВ не может быть меньше
DMB)
Следовательно, наше предположение
неверно. СМ-единственная.
(о существовании второй
перпендикулярной прямой
проходящей через данную точку)