10.21M

Category: $mathematics$ mathematics

Методика преподавания математики в 5 классе

1.

Методика преподавания
математики в 5 классе
Герасимов В.Д.
([email protected])

Основные вопросы
- Проблемы в работе с новым учебником
- Компоненты УМК для 5 класса
- Календарно-тематическое планирование
- Введение нового материала с использованием
учебного пособия и рабочей тетради
- Формирование культуры устных вычислений с
использованием математических тренажёров
- Методика обучения решению текстовых задач
- Примерное содержание самостоятельных и
контрольных работ

3.

Компоненты УМК для 5 класса:
1. Учебное пособие
2. Рабочая тетрадь
3. Сборник самостоятельных и контрольных
работ
4. Учебно-методическое пособие для учителя
5. Сборник практико-ориентированных задач
6. Планы-конспекты уроков
7. …

4.

Календарно-тематическое планирование:
возможности корректировки
Глава 1
§ 1. Как решать задачу (5 ч)…(7 ч)
§ 9. Умножение и деление натуральных чисел. Задачи на части (3
ч)…(5 ч)
Глава 3
§ 1. Дробные числа (3 ч)…(5 ч)
§ 9. Задачи на все действия с дробными числами (5 ч)
Один из уроков – введение задач на совместную работу.

5.

Темы:
«Округление натуральных чисел»
«Степень числа с натуральным показателем»
«Делители числа. Кратные числа. НОД и НОК
чисел»

6.

Тема
«Дробные числа»

7.

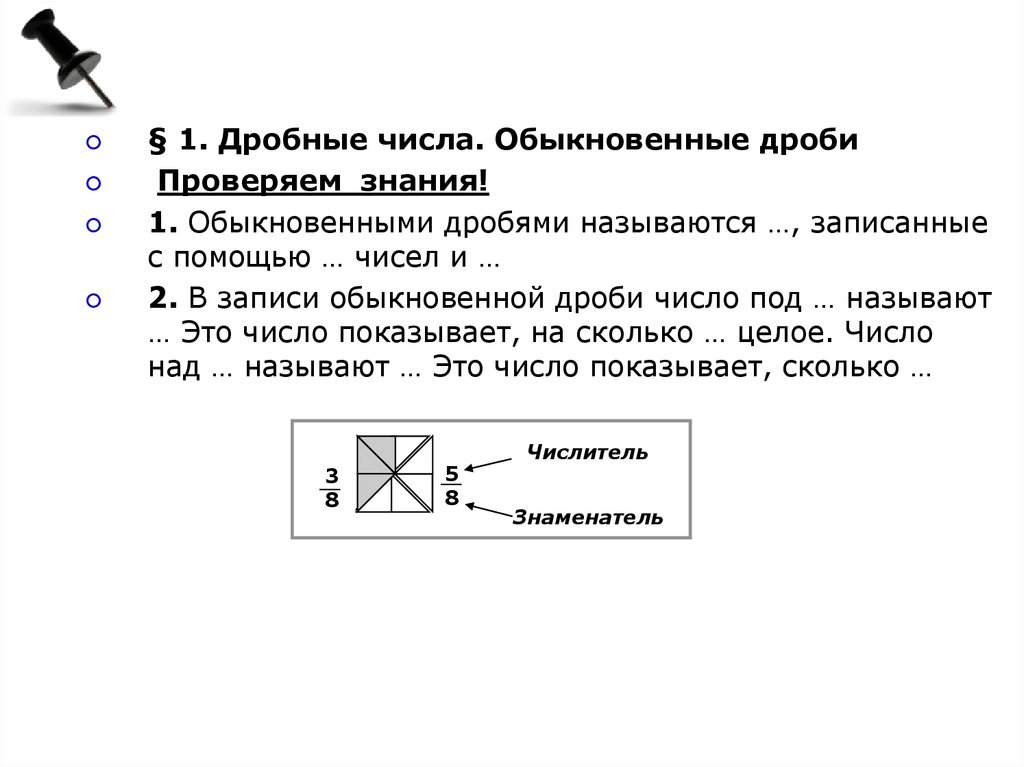
§ 1. Дробные числа. Обыкновенные дроби
Проверяем знания!
1. Обыкновенными дробями называются …, записанные
с помощью … чисел и …
2. В записи обыкновенной дроби число под … называют
… Это число показывает, на сколько … целое. Число
над … называют … Это число показывает, сколько …
3
8
5
8
Числитель
Знаменатель

8.

«Решаем самостоятельно»
1. Запишите дроби, которые соответствуют рисункам.

9.

«Решаем вместе»
2. Рассмотрите прямоугольник (целое). Выполните
задания:
а) закрасьте часть прямоугольника, которая соответствует дроби 1 ;
6
б) запишите дробь, которая соответствует другой части прямоугольника.
1
6
Решение. Дробь
1
6
?
?
означает, что прямоугольник надо разделить
на 6 равных частей и закрасить одну часть. Выполнить задание
можно разными способами:
1
6
5
6
1
6
5
6

10.

3. Рассмотрите фигуру (часть целого). Выполните
задания:
а) восстановите рисунок целого по его части и дроби, которая ей
соответствует;
б) запишите дробь, которая соответствует другой части целого.
2
6
?
?
Решение. Так как известна часть и соответствующая ей дробь, то
обращаем внимание на числитель дроби. Он показывает, что в
части целого содержится 2 равные части. Знаменатель дроби
показывает, что всего в целом 6 таких частей.
Выполнить задание можно разными способами:
2
6
4
6

11.

«Решаем самостоятельно»
4. Рассмотрите фигуру (целое). Закрасьте часть фигуры,
которая соответствует дроби. Запишите дробь, которая
соответствует другой части фигуры.
1
2
…
…
3
5
…
…
7
12
…
…
5. Рассмотрите фигуру (часть целого). Восстановите
рисунок целого по его части и дроби, которая ей
соответствует. Запишите дробь, которая соответствует
другой части фигуры.
2
3
…
…
8
12
…
…

12.

«Решаем вместе»
6. Найдите неизвестное значение величины (часть целого),
если известно, что она составляет 45 от числа 40 (целое).
Решение. В схематическом виде получаем: ? =
4
5
от 40
Отсюда вычисления: 40 : 5 · 4 = 32.
7. Найдите неизвестное значение величины (целое),
если известно, что её часть равна 40 и она составляет
всей величины.
Решение. В схематическом виде получаем: 40 =
Отсюда вычисления: 40 : 4 · 5 = 50.
4
5
4
5
от ?
от

13.

«Решаем самостоятельно»
8. Найдите неизвестное значение величины (часть целого),
4
если известно, какую дробь она составляет
от целого:
5
а) ? =
5
6
от 30
9. Найдите неизвестное значение величины (целое),
если известна её часть какую дробь она составляет от
целого:
а) 45 =
3
5
от ?
10. По схематической записи найдите неизвестное
значение величины:
а) ? =
2
5
б) 150 =
от 60
3
5
от ?

14.

«Решаем вместе»
11. В классе 28 учащихся, причём 4 всего класса
5
занимаются спортом. Сколько учащихся класса
занимаются спортом?
12. В школе отремонтировали 15 кабинетов, что составило
4
всего количества кабинетов. Сколько кабинетов в
5
школе?
17. В саду 24 дерева. 3 из них – груши, остальные –
8
яблони. Сколько груш в саду? Сколько яблонь в саду?
18. В спортзале занимались 20 мальчиков, что составляет
2 всех пятиклассников. Сколько всего пятиклассников
5
занимались в спортзале? Сколько занималось
девочек?

15.

Темы:
«Деление и дроби. Основное свойство
дроби»
«Сложение и вычитание обыкновенных
дробей»
«Сложение и вычитание смешанных чисел»

16.

Формирование культуры устных
вычислений с использованием
математических тренажёров

17.

Методика обучения решению
текстовых задач
- типология текстовых задач;
- подходы к построению модели задачи
и поиску её решения;
- проблема преемственности;
- решение задач с помощью уравнений.

18.

Основные типологии:
1) по количеству действий;
2) по соответствию числа данных и искомых;
3) по фабуле задачи;
4) по способам решения;
5) по виду отношений между значениями
величины (величин).

19.

Типология простых задач
I. Задачи на сложение и вычитание:
1) задачи, раскрывающие смысл операции сложения;
2) задачи, раскрывающие смысл операции вычитания;
3) задачи, раскрывающие связь между операциями сложения и вычитания;
4) задачи, раскрывающие смысл отношений «увеличить на» и «уменьшить на»;
5) задачи, раскрывающие смысл отношений «больше на» и «меньше на»;
II. Задачи на умножение и деление:
1) задачи, раскрывающие смысл операции умножения;
2) задачи, раскрывающие смысл операции деления;
3) задачи, раскрывающие связь между операциями умножения и деления;
4) задачи, раскрывающие смысл отношений «увеличить в» и «уменьшить в»;
5) задачи, раскрывающие смысл отношений «больше в…раз» и «меньше в…раз»;

20.

Типология простых задач
(по виду отношений между значениями величины
(величин))
В условии одно из отношений:
1) «всего (вместе)»;
2) «больше на (меньше на)»;
3) «больше в (меньше в)»;
4) «дробное отношение»;
5) «среднее арифметическое чисел»;
6) «пропорциональность».
7) «было – изменение – стало»;
8) «деление поровну (на равные части)»;
9) «геометрическая фигура»;
10) «числовые зависимости».

21.

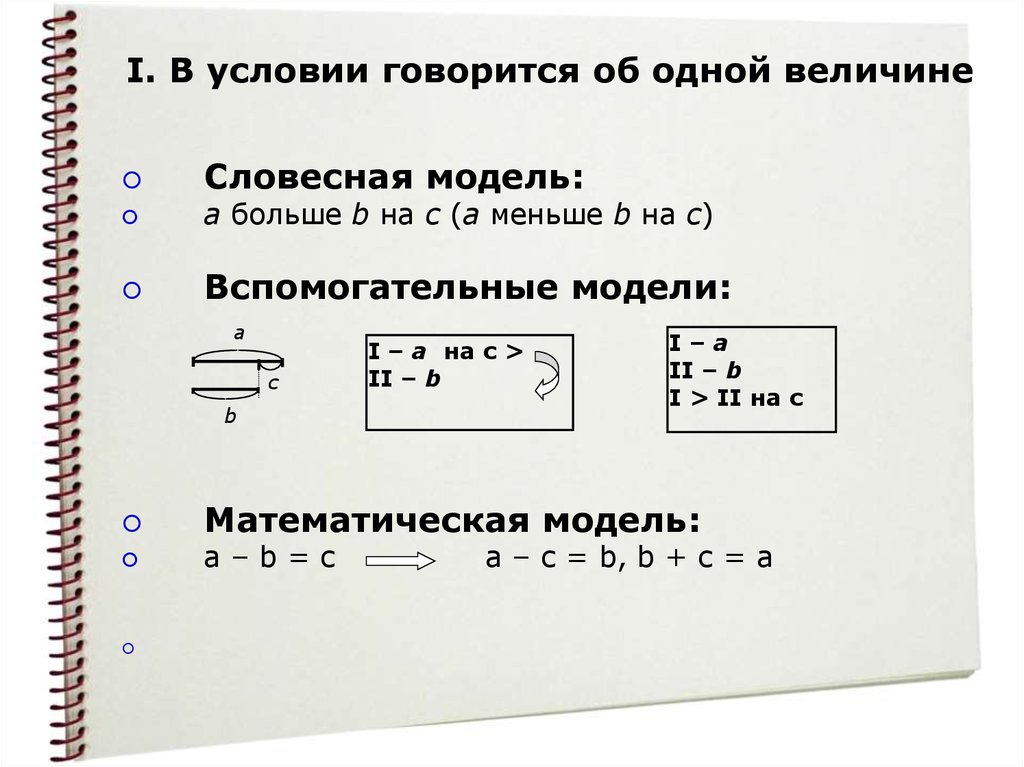
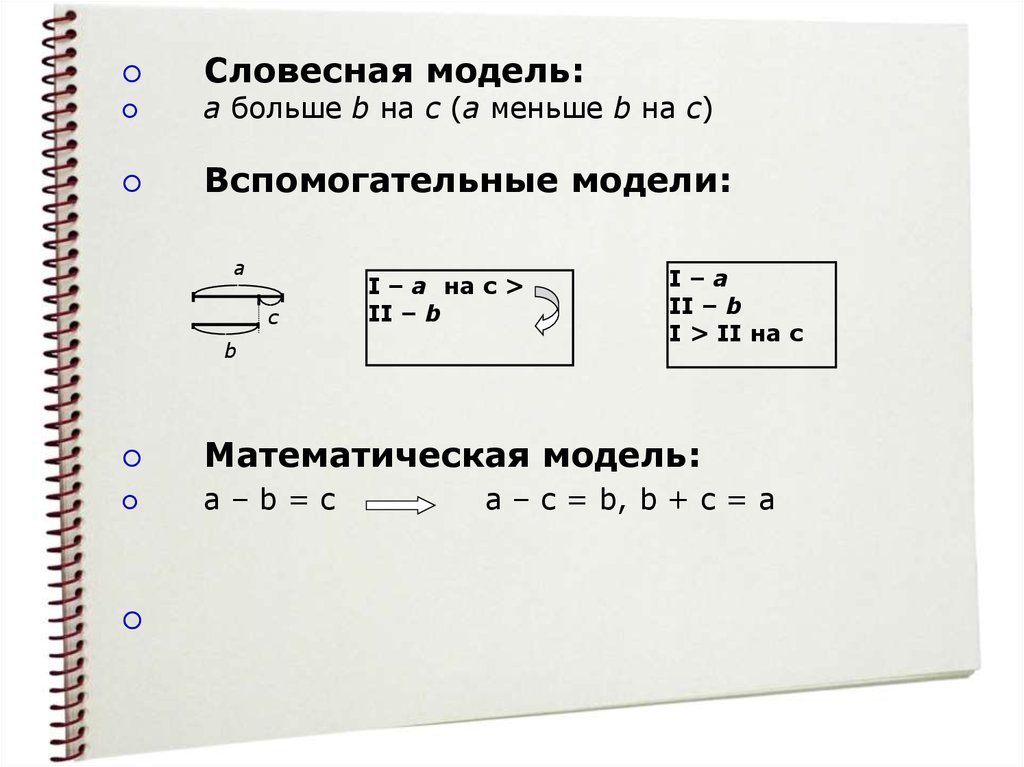
I. В условии говорится об одной величине
Словесная модель:
a больше b на с (a меньше b на с)
Вспомогательные модели:
а
с
b
I – а на с >
II – b
I–а
II – b
I > II на с
Математическая модель:
a–b=c
a – c = b, b + c = a

22.

Словесная модель:
a больше b в с раз (a меньше b в с раз)
Вспомогательные модели:
a
I – а > b в с раз
II – b
I–а
II – b
I > II в с раз
b
Математическая модель:
a:b=c
a : c = b, b · c = a

23.

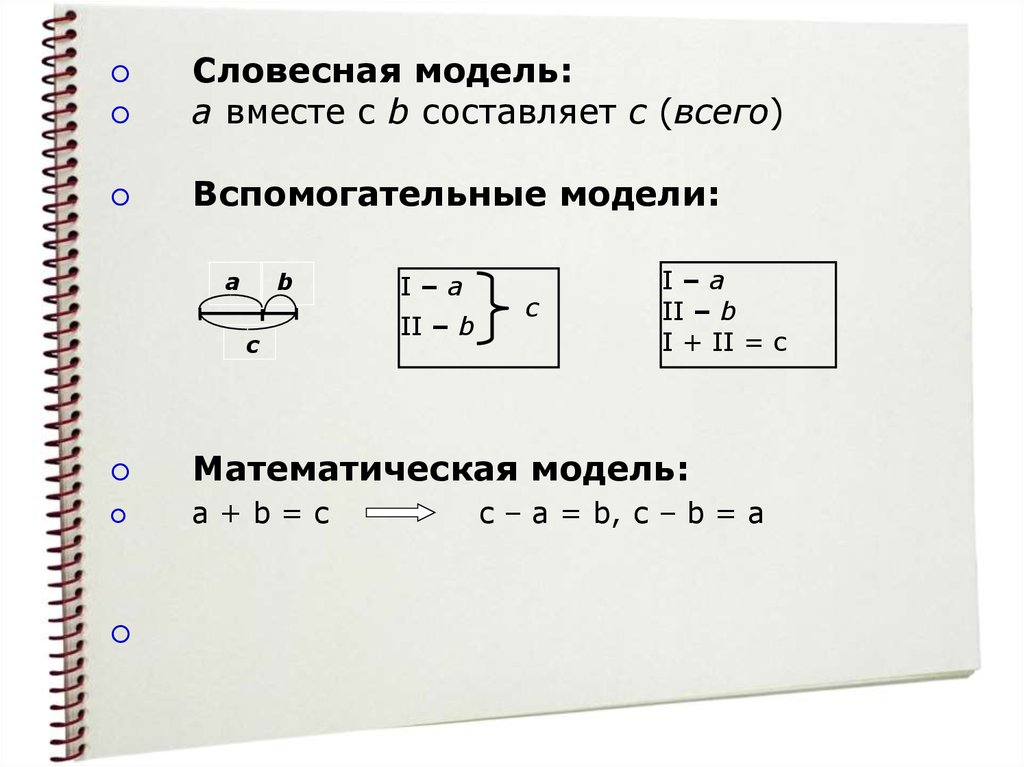
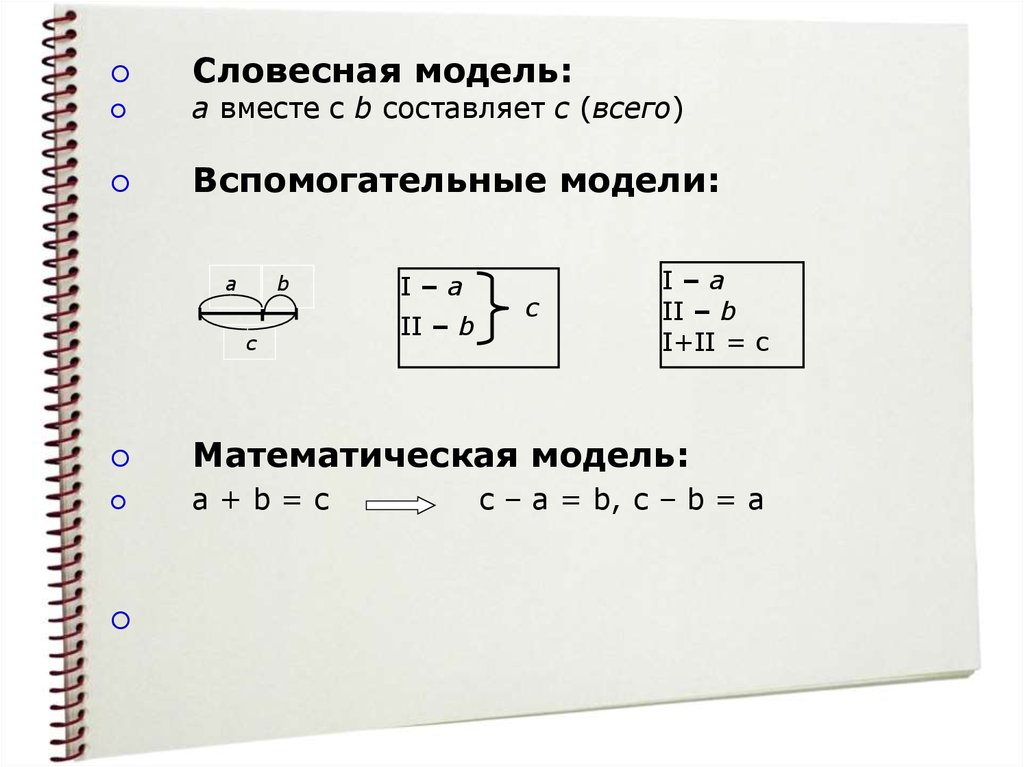
Словесная модель:
a вместе с b составляет с (всего)
Вспомогательные модели:
a
b
с
I–а
II – b
c
I–а
II – b
I + II = с
Математическая модель:
a+b=c
с – а = b, с – b = a

24.

Словесная модель:
Было а, уменьшилось на b, осталось с
Вспомогательные модели:
а
с
b
Было
а
Уменьшилось b
Стало
с
Б
а
Математическая модель:
a–b=c
И (–) С
b
с
a – c = b, b + c = a

25.

Словесная модель:
Было а, увеличилось на b, стало с
Вспомогательные модели:
а
с
b
Было
а
Увеличилось b
Стало
с
Б
а
Математическая модель:
a+b=c
И (+) С
b
с
с – а = b, с – b = a

26.

Словесная модель:
a составляет
Вспомогательные модели:
m
n
от с
c
с
m
n
а
а
b
a=
m
n
Математическая модель:
a=
m
·c
n
с=а:
m
n
,
m
=a:с
n
m
от с
n

27.

II. В условии задачи говорится о двух
величинах (геометрические величины)
Словесная модель:
Периметр P прямоугольника со сторонами a и b
Вспомогательная модель:
a
b
Математическая модель:
P = (a + b) · 2

28.

Словесная модель:
Площадь S прямоугольника со сторонами a и b
Вспомогательная модель:
a
b
Математическая модель:
S=a·b

29.

III. В условии задачи говорится о трёх
величинах (задачи на процессы)

30.

Словесная модель:
Процесс сортировки: размещение, распределение
некоторого количества объектов ОК поровну в К
групп, по К1 объектов в каждую
Вспомогательная модель:
К
1
а
К
ОК
b
c
Математическая модель:
К1 · К = ОК
К1 = ОК : К
К = ОК : К1

31.

Словесная модель:
Процесс торговли: покупка (продажа) товара
стоимостью С в количестве К единиц (массой К) и
ценой Ц
Вспомогательная модель:
Ц
а
К
С
b
c
Математическая модель:
Ц·К=С
Ц=С:К
К=С: Ц

32.

Словесная модель:
Процесс движения: прохождение
скоростью v в течение времени t
Вспомогательная модель:
v
а
t
b
s
c
Математическая модель:
v· t=s
пути
v=s: t
t=s:v
s
со

33.

Словесная модель:
Процесс работы: выполнение некоторого объёма
работы ОК в течение определённого количества
времени К с производительностью К1
Вспомогательная модель:
К
1
а
К
ОК
b
c
Математическая модель:
К1 · К = ОК
К1 = ОК : К
К = ОК : К1

34.

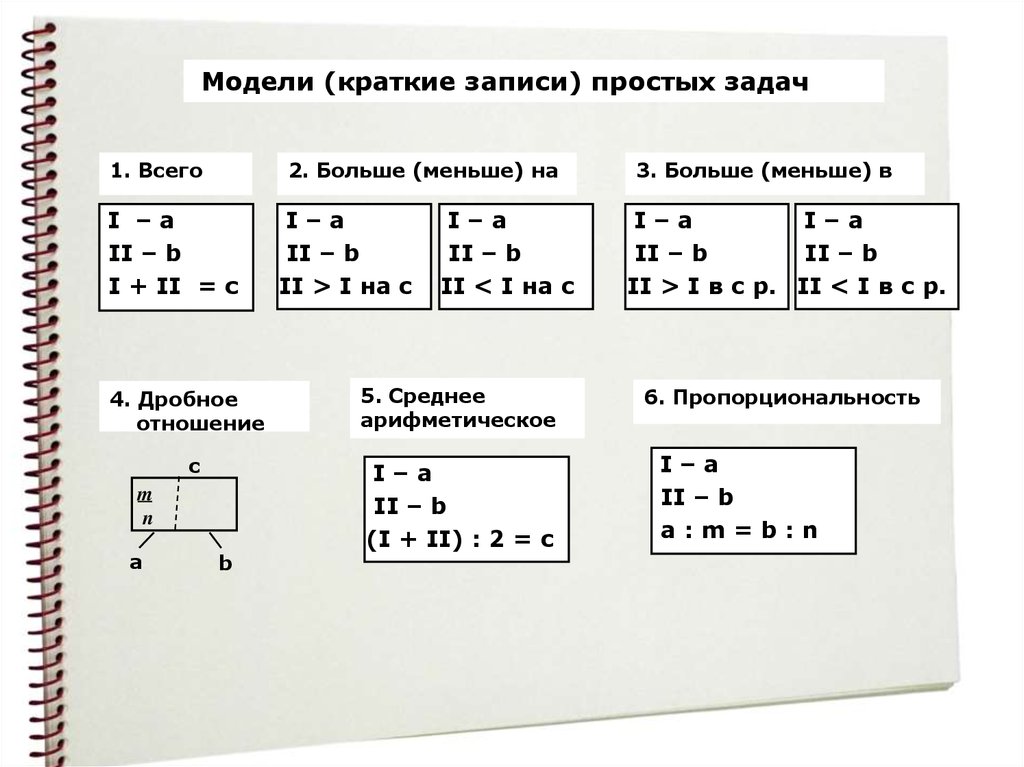
35.

Модели (краткие
записи) простых
задач
Авторская
типология
простых
задач
1. Всего
2. Больше (меньше) на
I –а
II – b
I + II = с
4. Дробное
отношение
c
m
n
а
b
I–а
II – b
II > I на c
I–а
II – b
II < I на c
5. Среднее
арифметическое
I–а
II – b
(I + II) : 2 = c
3. Больше (меньше) в
I–а
I–а
II – b
II – b
II > I в c р. II < I в c р.
6. Пропорциональность
I–а
II – b
a:m=b:n

36.

Модели (краткие записи) простых задач
7. «Было – изменение – стало»
Б
a
И (-) С
b
c
Б
И (+)
a
b
8. Процессы
К1
С
К
ОК
b
c
a
c
9. «Геометрическая фигура»
а1
а2
a
а1
a
b
а2
L = а1 + а2
L
P = 2(a + b)
a
b
b
P
a
…
b
c
P=a+b+
c
c
10. «Числовые зависимости»
x+a= b
x-a= b
x·a= b
a:x= b
…

37.

Основные типы составных задач
I. Задачи с одной величиной, в условии которых
говорится о двух и более отношениях между
значениями этой величины
II. Задачи с одной величиной, в условии которых
говорится об отношении «было-изменениестало» и других отношениях
III. Задачи на процессы
IV. Задачи с геометрическим содержанием
V. Задачи на числовые зависимости
VI. Задачи, в условии которых имеют место
разные виды отношений

38.

I. Задачи с одной величиной, в условии
которых говорится о двух и более
отношениях между значениями этой
величины
I + II =
II > I на
I
II
I + II + III =
II > I на
III < II в
I
II
III
I + II + III + IV =
II < I на
III > I + II в
IV = I + III
I
II
III
IV
Задача. Первое из неизвестных чисел составляет 140 %
второго, а отношение первого к третьему равно
14 :11 . Найти эти числа, если разность между
третьим и вторым на 40 единиц меньше числа,
составляющего 12,5 % суммы первого и второго
чисел.

39.

II. Задачи с одной величиной, в условии
которых говорится об отношении «былоизменение-стало» и других отношениях
между значениями этой величины
Б
I
II
И
(+)
(-)
С
другие отношения
Задача. Количество книг на первой полке в 3 раза
меньше, чем на другой. Если с первой полки взять 7
книг, а на вторую поставить 9, то количество книг на
первой полке будет в 5 раз меньше, чем на второй.
Сколько книг было на каждой полке первоначально?

40.

III. Задачи на процессы (в условии говорится
об отношении между тремя взаимосвязанными
величинами, а так же об отношениях между
значениями некоторых из этих величин)
К1
К
ОК
I
II
другие отношения
Задача. Несколько детей разделили поровну между собой
28 конфет. Если бы число детей было на 3 меньше,
то каждый получил бы дополнительно 3 конфеты.
Сколько было детей?

41.

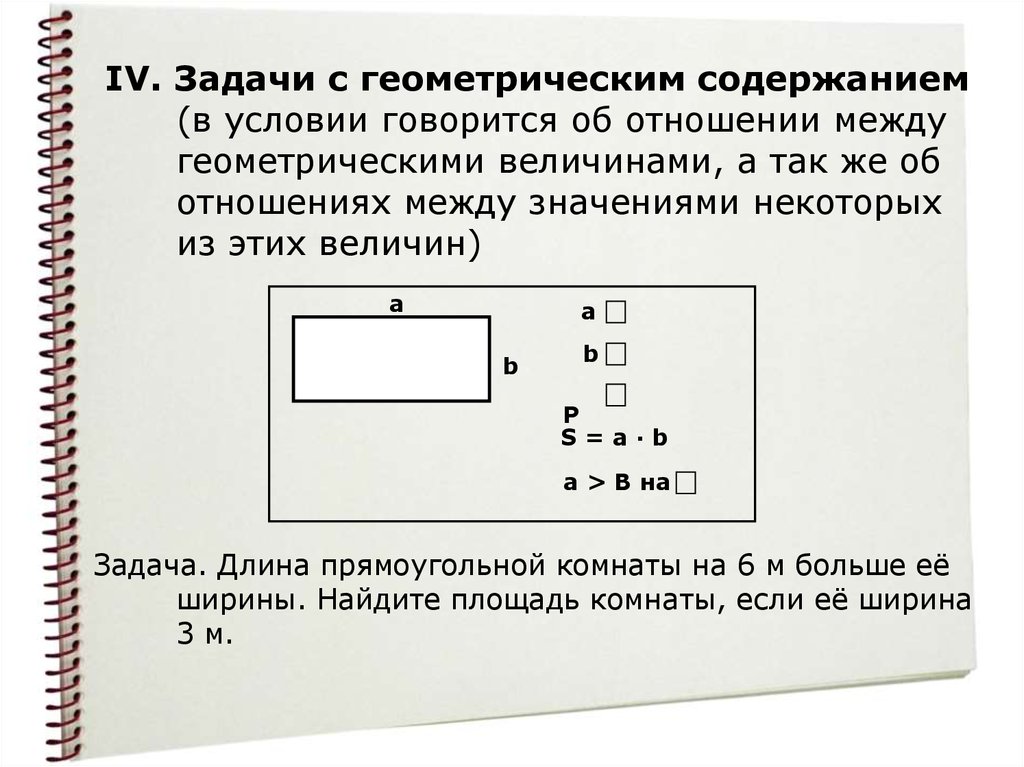
IV. Задачи с геометрическим содержанием
(в условии говорится об отношении между
геометрическими величинами, а так же об
отношениях между значениями некоторых
из этих величин)
a
a
b
b
P
S=a·b
a > B на
Задача. Длина прямоугольной комнаты на 6 м больше её
ширины. Найдите площадь комнаты, если её ширина
3 м.

42.

V. Задачи на числовые зависимости
(x – a) : b = c
a : b = с (ост. к)
a–x:b=c
a b = 10a + b
a<b в
раз
ba > ab на
a
b
Задача. 96 разделили на задуманное число и полученное
частное увеличили на 84. В результате получили
100. Найдите задуманное число.
Задача. Сумма цифр двузначного числа равна 14. Если эти
цифры поменять местами, то полученное число будет
меньше исходного на 18. Найдите первоначальное
число.

43.

VI. Задачи, в условии которых имеют место
разные отношения
(практико-ориентированные задачи)
Задача. Когда от рулона шёлка отрезали 36 м, чтобы
сшить несколько одинаковых костюмов, то ткани в
нём осталось на 8 таких же костюмов. Сколько
костюмов уже сшили, если в рулоне было 68 м
ткани?
Б
68 м
К1
?
И(–)
К
ОК
?
36 м
К1
?
С
К
8 к.
ОК
?

44.

Особенности построения рабочей
тетради и её использования для
реализации методики обучения
решению текстовых задач
2.1 Раздел «Проверяем знания!»
2.2 Раздел «Решаем вместе»
2.3 Раздел «Решаем самостоятельно»

45.

§ 1. Как решать задачу
Проверяем знания!
1. В условии задачи говорится об одной величине.
Пусть a, b и с – значения этой величины.
Расскажите:
а) какими зависимостями (отношениями) могут быть
связаны значения a, b и с;
б) как найти каждое из значений величины, зная два
других.
Таблица (часть 1). Основные виды зависимостей
(отношений) между значениями одной величины и их
модели

46.

Словесная модель:
a больше b на с (a меньше b на с)
Вспомогательные модели:
а
с
b
I – а на с >
II – b
I–а
II – b
I > II на с
Математическая модель:
a–b=c
a – c = b, b + c = a

47.

Словесная модель:
a вместе с b составляет с (всего)
Вспомогательные модели:
a
b
с
I–а
II – b
c
I–а
II – b
I+II = с
Математическая модель:
a+b=c
с – а = b, с – b = a

48.

49.

«Решаем вместе»
2. В мотке было некоторое количество метров
проволоки. После того как отрезали 19 м,
осталось 34 м. Сколько метров проволоки было
в мотке?
В условии задачи говорится об одной величине: «длине
проволоки». Рассматриваются три её значения: «было в
мотке» (значение неизвестно), «отрезали от мотка»
(значение известно – 19) и «осталось в мотке» (значение
известно – 34).
Связь между значениями величины выражена словами:
«было», «изменилось» (уменьшилось) и «стало».Модель
задачи можно сделать одним из следующих способов:

50.

?м
34 м
19 м
Было
– ?м
Отрезали – 19 м
Осталось – 34 м
Решение. 34 + 19 = 53 (м).
Ответ: 53 м.
Б
?
И (–)
19 м
С
34 м

51.

4 (№ 28). Папа с сыном принесли с рыбалки 37
рыб: щук, лещей и окуней. Окуней было на 13
больше, чем щук, а лещей и окуней вместе – 29
рыб. Сколько рыб каждого вида принесли отец и
сын?
В условии задачи говорится об одной величине:
«количестве рыб, которое принесли с рыбалки».
Рассматриваются три её значения: «количество щук»,
«количество лещей», «количество окуней»; все они
неизвестны.
Также в условии задачи речь идёт о следующих
отношениях между значениями величины: «всего
принесли с рыбалки 37 рыб», «окуней было на 13
больше, чем щук», «лещей и окуней вместе – 29 рыб».

52.

Если отношения между значениями величины перевести
на язык схематических записей, то модель задачи
можно сделать в следующем виде:
I (щуки) – ?
II (лещи) – ?
III (окуни) – ?
I + II + III = 37 р.
III > I на 13 р.
II + III = 29 р.
Решение.
1) 16 · 2 = 32 (к.) — во второй день;
2) 16 + 32 = 48 (к.) — в третий день;
3) 16 + 32 + 48 = 96 (к.)—всего или 3) 48+48=96 (к.)
Ответ: 96 кустов роз.

53.

5. Помидоры разложили в две корзины так,
что в одной из них оказалось 48 помидоров.
После того, как в эту корзину переложили из
второй 7 помидоров, в ней стало на 26
помидоров больше, чем во второй корзине.
Сколько помидоров было сначала во второй
корзине?
В условии задачи говорится о «количестве помидоров».
Разобраться, какие значения величины известны и
неизвестны, какими отношениями они связаны,
поможет составление краткой записи задачи в виде
таблицы.

54.

Обращаем внимание на слова «разложили»,
«переложили», «стало». Значит, значения величины
связаны отношением «было – изменилось – стало».
Рассматривается две ситуации: «первая корзина»,
«вторая корзина». Записываем знаки: в первую
корзину добавили помидоров – пишем знак «+», из
второй корзины забирали помидоры – пишем знак «–».
Записываем значения величины: для известных
значений – пишем число, для неизвестных – ставим
знак вопроса.
Отношение «в ней стало на 26 помидоров больше, чем
во второй корзине» записываем в соответствующем
столбике таблицы. Обводим главный вопрос задачи.

55.

Было
I 48 п.
II ? п.
Изменилось
(+) 7 п.
(-) 7 п.
Стало
?
?
I > II на 26 п.
Б
И
С
I 48 п. (+) 7 п.
?
II ? п. (-) 7 п.
?
I > II на 26 п.
Решение.
1) 48 + 7 = 55 (п.) – стало в первой корзине;
2) 55 – 26 = 29 (п.) – стало во второй корзине;
3) 29 + 7 = 36 (п.) – было во второй корзине.
Ответ: 36 помидоров.

56.

«Решаем самостоятельно»
Дополните модель задачи и решите её (6 – 11)
9 (№ 29). Сумма трёх чисел равна 55. Сумма
первого и второго равна 32, а разность третьего и
первого равна 8. Найдите эти числа.
I – …
II – …
III – …
I + II + III = …
I + II = …
III – I = …

57.

10 (№ 27). В шахматной секции занимались
мальчики и девочки, причём мальчиков было на 5
меньше, чем девочек. После того, как 8 девочек и
несколько мальчиков перешли в секцию по
плаванию, остались играть в шахматы 7 девочек и
6 мальчиков. Сколько мальчиков ушло в секцию по
плаванию?
Б
И
I (мальчики) …
(-) ?
II (девочки) …
(-) 8 д.
I < II на …
С
…
…

58.

Проверяем знания!
1. В условии задачи говорится о процессе:
а) сортировки; б) торговли; в) движения;
г) выполнения работы.
Для каждого вида процесса расскажите:
– какими тремя величинами характеризуется процесс
и как эти величины можно обозначить;
– какая зависимость (формула) связывает данные
величины;
– как найти значение каждой величины, зная
значения двух других.
Таблица (часть 3). Основные виды зависимостей
между значениями трёх величин и их модели

59.

Словесная модель:
Процесс
Вспомогательные модели:
сортировки:
размещение, распределение
некоторого количества объектов ОК поровну в К групп, по
К1 объектов в каждую
К
1
а
К
ОК
b
c
Математическая модель:
К1 · К = ОК
К1 = ОК : К, К = ОК : К1

60.

Словесная модель:
Процесс торговли: покупка (продажа) товара
стоимостью С в количестве К единиц (массой К) и
ценой Ц
Вспомогательные модели:
Ц
а
К
С
b
c
Математическая модель:
К1 · К = ОК
К1 = ОК : К, К = ОК : К1

61.

«Решаем вместе» (простые задачи)
15. Скорость поезда 74 км/ч. Какое расстояние
поезд проедет за 5 ч?
В условии задачи речь идёт о трёх величинах: «скорости
движения» (обозначается V), «времени» (обозначается t)
и «пройденном расстоянии (пути) » (обозначается S).
Число 74 – значение скорости, число 5 – значение
времени; неизвестное число – пройденный путь.
Зависимость между значениями величин – формула,
связывающая путь, время и скорость: S = V · t .
Модель задачи удобно сделать в виде таблицы:
Скорость (V)
74 км/ч
Время (t)
Расстояние (S)
5ч
? км
Можно использовать сокращённый вариант таблицы:
V
74 км/ч
t
5ч
s
?

62.

16. В 7 подъездах дома 441 квартира, в каждом
Подъезде поровну. Сколько квартир в одном
подъезде?
В условии задачи речь идёт о трёх величинах:
«количестве квартир в одном подъезде» (можно обозначить
К1), «количестве подъездов» (можно обозначить К),
«общем количестве квартир» (можно обозначить ОК).
Число 441 – целое (дом), состоящее из одинаковых частей
(подъездов); число 7 – количество подъездов; количество
квартир в подъезде неизвестно. Зависимость между
значениями величин записывается формулой: ОК = К1 · К.
Для составления модели задачи используем сокращённый
вариант таблицы таблицы:
К1
? кв.
К
ОК
7 п.
441 кв.

63.

«Решаем самостоятельно»
17. Для данного условия выберите модель, составленную с
помощью таблицы.
1) Группа школьников села в 3 одинаковых автобуса,
заполнив все сидячие места. В каждом автобусе по 45 мест.
а)
К1
45
К
?
ОК
б)
3
К1
45
К
3
ОК
в)
?
К1
?
К
3
ОК
45
2) Для секции футбола купили 8 мячей по одинаковой
цене. За покупку заплатили 120 р.
а)
Ц
120
К
8
С
3
б)
Ц
8
К
?
С
120
в)
Ц
?
К
8
С
120

64.

«Решаем самостоятельно»
Дополните модель задачи и решите её (18 – 19)
18. Лена купила несколько ручек по 3 р. за каждую,
затратив на покупку 15 р. Сколько ручек купила Лена?
Ц
…
К
…
С
…
19. Самолёт за 4 ч пролетел 2 984 км. Какова скорость
самолёта?
v
…
t
…
s
…

65.

«Решаем вместе» (составные задачи)
20. Для школы купили 2 телевизора и 4
планшета. За всю покупку заплатили 756 р. Цена
телевизора 270 р.Сколько стоит планшет?
В условии задачи речь идёт о трёх величинах: «цене
товара» (можно обозначить Ц), «количестве единиц
товара» (можно обозначить К); «стоимости всей покупки»
(обозначим С). Рассматриваются значения этих величин для
двух видов товара: «телевизоры» и «планшеты».
Зависимость между значениями величин–формула: С = Ц · К.
Обратим так же внимание на слова «за всю покупку
заплатили 756 р.». Значит, значения стоимостей товаров
связаны отношением «всего (вместе)».
Ц
I (тел.)
II (план.)
К
С
270 р
2 т.
?
? р.
4 пл.
?
I + II = 756 р.

66.

«Решаем самостоятельно»
23 (№ 24). В трёх одинаковых автобусах 78
сидячих мест. Сколько сидячих мест в шести
таких автобусах?
К1
К
ОК
I
…
3 авт.
…
II
…
…
…

67.

«Решаем самостоятельно»
25 (№ 44). Велосипедист и всадник отправились из
спортивной базы в лагерь отдыха разными дорогами.
Всадник выбрал дорогу, которая короче на 9 км, его
скоростью на 3 км/ч меньше, чем скорость
велосипедиста. Велосипедист затратил 3 часа, чтобы со
скоростью 18 км/ч преодолеть путь от спортивной базы
до лагеря отдыха. Кто их них раньше приедет в лагерь
отдыха?
v
t
I (велосип-т.)
…
3ч
…
II (всадник)
…
…
…
II < I на 3 км/ч
s
II < I на …

68.

Задачи из учебного пособия
7 (84). Необходимо налить 12 000 литров воды в бассейн.
Через первую трубу бассейн наполняется за 10 ч, через
вторую трубу – за 15 ч. За какое время можно наполнить
бассейн через две трубы?
К1
К
ОК
I
?
10 ч
12 000 л
II
…
…
…
III (вместе)
?
?
12 000 л
III = I + II

69.

Задачи из учебного пособия
7 (115). От автостанции одновременно
выехали противоположных направлениях автобус
и такси. Скорость такси 80 км/ч, а скорость автобуса
в 2 раза меньше. Через сколько часов расстояние
между ними составит 480 км?
80 км/ч
?
?
?
?
?
480 км

70.

«Решаем вместе»
6. Для приготовления напитка берут 3 части сиропа и 7
частей кипячёной воды. Сколько граммов сиропа надо
взять, чтобы получить 600 г напитка?
В задаче напиток получают из двух других продуктов (сиропа
и кипяченой воды). Перед смешиванием каждый из продуктов
как бы «делится на равные части», которые затем смешиваются
в необходимых количествах. При этом массы одной части
каждого продукта считают одинаковыми.
На модели с помощью отрезков это выглядит так:
сироп
вода
? кг
? кг
600 г

71.

Решение задач
с помощью уравнений

72.

Решение задач составлением уравнения
Задача. Петя прочитал рассказ и повесть: всего 120
страниц. Повесть занимает в 5 раз больше страниц, чем
рассказ. Сколько страниц занимает рассказ
и сколько – повесть?
Р + П = 120 c.
П > Р в 5 р.
Р– ?
П– ?
Р– ?
П– ?
Р + П = 120 c.
П > Р в 5 р.

73.

Решение задач составлением уравнения
Петя прочитал рассказ и повесть: всего 120 страниц.
Повесть занимает в 5 раз больше страниц, чем рассказ.
Сколько страниц занимает рассказ и сколько – повесть?
Р + П = 120 c.
П > Р в 5 р.
Р ? х
П ? х · 5 = 5х
5 · x + x = 120
5 · x + 1 · x = 120
x · (5 + 1) = 120
6 · x = 120
x = 120 : 6
x = 20; 5 · x = 100

74.

Решение задач составлением уравнения
Задача. В синем мешке было орехов в 4 раза больше,
чем в красном, причем в красном мешке их было на 15 кг
меньше, чем в синем. Сколько килограммов орехов было в
синем мешке?
С > К в 4 р.
К < С на 15 кг
С– ?
К–?
С– ?
К– ?
С > К в 4 р.
К < С на 15 кг

75.

Решение задач составлением уравнения
В синем мешке было орехов в 4 раза больше, чем
в красном, причем в красном мешке их было на 15 кг
меньше, чем в синем. Сколько килограммов орехов было
в синем мешке?
С > К в 4 р.
К < С на 15 кг
С ? х · 4 = 4х
К ? x
С – К = 15
4 · x – x = 15
4 · x – 1 · x = 15
x · (4 – 1) = 15
3 · x = 15
x = 15 : 3
x = 5; 4 · x = 20

76.

Решение задач составлением уравнения (6 – 7 класс)
Задача. На верхней полке в 3 раза больше книг, чем на
нижней. После того, как с верхней полки сняли 15
книг, а на нижнюю поставили 11 книг, на обеих
полках книг стало поровну. Сколько книг было на
каждой полке первоначально?
Б
I
?
в
II
н
И
С
x
(– )
15 к.
? x – 15
? 3x
(+)
11 к.
? 3x + 11
I > II в 3 р.
х – 15 = 3х + 11
I = II

77.

Решение задач на процессы составлением
уравнения
Задача. Дети выкопали на пришкольном участке 264
кг картофеля. Часть его разложили в 6 больших
сеток, а остальной картофель — в 9 маленьких.
Сколько килограммов картофеля разложили в
большие сетки, если масса маленькой сетки в 4 раза
легче массы большой?
К1
Iб
IIм
К
? x·4 = 4·х
?x
II < I в 4 р.
ОК
6 с.
9 с.
? 4·х·6=24·x
? 9·х
I + II = 264 кг
24 · х + 9 · х = 264

78.

Решение задач на процессы составлением
уравнения
Задача. Расcтояние между городами 1200 км. Поезд
на первом участке шёл со скоростью в 2 раза
меньшей, чем на втором. Какова была скорость
поезда на втором участке, если известно, что
первый участок поезд прошёл за 8 ч, а второй — за
6 ч?
V
I
II
t
?х
8ч
? 2·х
6ч
I < II в 2 р.
S
? 8·х
? 6·2х= 12·х
I + II = 1200км
8 · х + 12 · х = 1200

79.

Задачи на совместную работу (глава 3, § 9)
Задача. Один мастер может выполнить работу за 30 мин, а
второй за 20 мин. За сколько минут они могут выполнить
работу, работая вместе?
Задача. Через первую трубу бассейн можно заполнить за 30 ч,
а через вторую за 20 ч. За сколько часов наполнится
бассейн через обе эти трубы?
I
II
III
К1
?
?
?
III = I + II
К
30 ч
20 ч
?
ОК
?1
?1
?1
I = II = III =
1

80.

Задача. Работу по ремонту дома первая бригада может
выполнить за 6 дней, вторая – за 9 дней. После
нескольких дней совместной работы вторая бригада
была переведена на новый объект, а первая
завершила работу за 1 день. За сколько дней был
отремонтирован дом?
I
II
III
IV1
К1
?
?
?
III = I + II
(I + II)
IV2 (I)
К
6 д.
9 д.
?
ОК
?1
?1
?1
?
?
?
?
1 д.
?
IV1 + IV2 = ?
IV1 + IV2 =1

81.

6 – 8 классы
1(6.3.41а). Несколько детей разделили поровну между собой
28 конфет. Если бы число детей было на 3 меньше, то
каждый получил бы дополнительно 3 конфеты. Сколько
было детей?
2(6.3.11б). Из-за 10-минутной задаржки поезда в пути ему
пришлось на перегоне в 60 км увеличить скорость на 5
км/ч. Найдите первоначальную скорость поезда.
3(6.3.33а). Две наборщицы должны были набрать по 60
страниц каждая. Вторая наборщица набирала за 1 час на 2
страницы меньше, чем первая, поэтому закончила работу на
1 час позже. Сколько страниц в час набирала первая
наборщица?
4(6.5.18а). Скорость поезда увеличилась от 70 км/ч до
90 км/ч. На сколько процентов уменьшилось время,
затрачиваемое поездом на один и тот же путь?

82.

6 – 8 классы
5.
Двое рабочих, работая вместе, выполняют некоторую
работу за 8 ч. Первый из них, работая отдельно, может
выполнить всю работу на 12 ч скорее, чем второй, если
тот будет работать отдельно. За сколько часов каждый из
них, работая порознь, может выполнить работу?
6.
Бассейн заполняется водой при помощи двух труб. Когда
первая труба проработала 7 ч, включили вторую трубу.
Вместе они проработали 2 ч. За сколько часов может
наполнить бассейн каждая труба, работая отдельно, если
первой нужно на это на 4 ч больше, чем второй?
7.
Производительности двух тракторов относятся как 2 : 3.
Работая вместе, они вспашут поле за 12 ч. За сколько
часов вспашет поле каждый трактор, работая отдельно?

83.

6 – 8 классы
8. Бассейн заполняется водой при помощи двух труб. Когда
первая труба проработала 7 ч, включили вторую трубу.
Вместе они проработали 2 ч. За сколько часов может
наполнить бассейн каждая труба, работая отдельно, если
первой нужно на это на 4 ч больше, чем второй?
9.
За 3,5 ч работы один штамповочный пресс может
изготовить 42% всех заказанных деталей. Второй пресс за
9 ч работы может изготовить 60% всех деталей, а скорости
выполнения работы на третьем и на втором прессах
относятся как 6 : 5. За какое время будет выполнен весь
заказ, если все три пресса будут работать одновременно?
10. Мастер и ученик, работая вместе, заканчивают задание
на 1 час раньше, чем мастер, работая один, но на полчаса
позже, чем мастер и два ученика. За какое время
выполняют задание два мастера и ученик?