Nauczanie Łamigłówkowe
1. Nauczanie Łamigłówkowe
Wykład 32. Modelowanie: pomyślmy o problemie trochę więcej
Rozdział #3:MODELOWANIE: POMYŚLMY O PROBLEMIE
TROCHĘ WIĘCEJ
2
3. Zagadka 3.2
• Stoisz przy drzwiach, prowadzących do pustego pokoju, w którym usufitu wiszą trzy żarówki. Wszystkie trzy żarówki są wyłączone. Na
zewnętrznej ścianie pokoju, przy drzwiach są trzy przełączniki, z
których każdy włącza i wyłącza inną żarówką (zatem między każdym
przełącznikiem a każdą żarówką jest związek jeden do jednego).
Wszystkie trzy przełączniki są ustawione w pozycji „wyłączony”.
Twoim zadaniem jest ustalenie, którym przełącznikiem włącza się
którą żarówkę. Wolno Ci operować przełącznikami, ale niezależnie
od tego, co z nimi zrobisz, nie możesz zobaczyć, co się dzieje
w pokoju. Gdy jesteś usatysfakcjonowany, otwierasz drzwi
i wchodzisz do pokoju. Możesz dokładnie obejrzeć pokój i bez
wychodzenia z pokoju ani ponownego dotykania przełączników
musisz ustalić, który przełącznik jest podłączony do której żarówki.
3
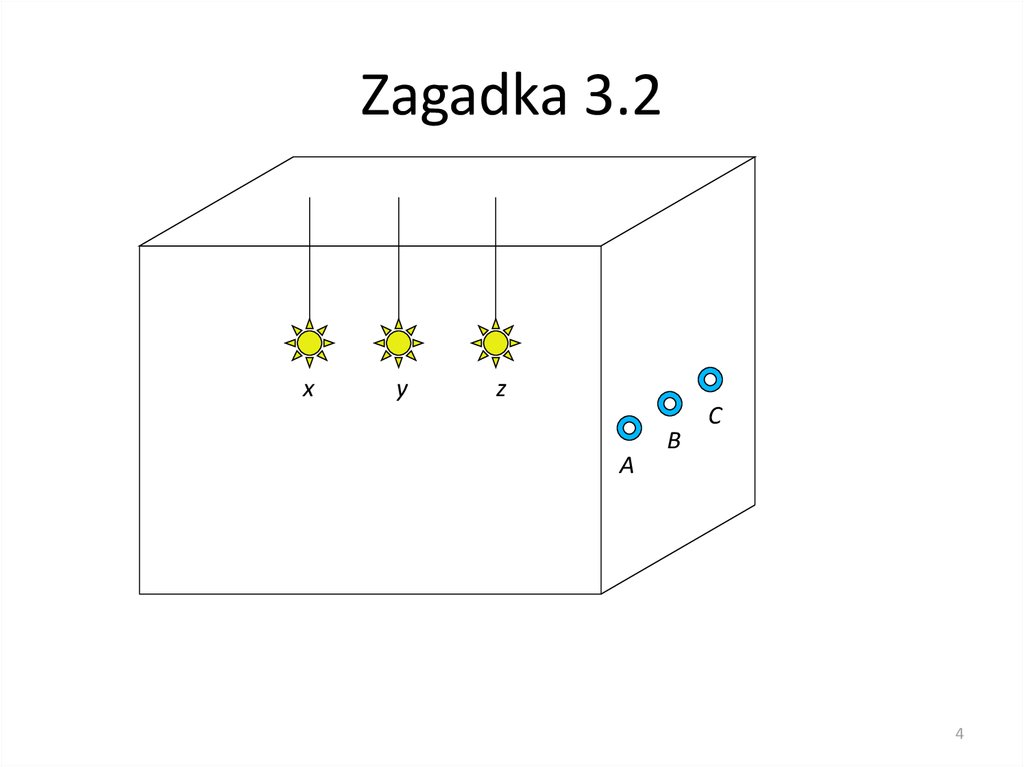
4. Zagadka 3.2
xy
z
A
B
C
4
5. Zagadka 3.2
Przełączniki:Możliwe ustawienia:
A
1
1
1
1
B
1
1
0
0
C
1
0
1
0
1 – włączony, 0 – wyłączony
0
1
1
0
1
0
0
0
1
0
0
0
• Jak ustalić, który przełącznik jest podłączony do której żarówki?
Rozwiązanie pod koniec wykładu.
5
6. Ważne spostrzeżenie
• Rozwiązywanie problemów światarzeczywistego jest procesem dwuetapowym:
Problem
Model
Rozwiązanie
Reguła# 1: bądź pewien, że rozumiesz problem oraz wszystkie
podstawowe pojęcia i wyrażenia jakie zostały użyte do jego
zdefiniowania.
6
7. Zagadka 3.3
• Jest sobie podkowa z sześcioma otworami nagwoździe:
• Wykonaj dwa prostoliniowe cięcia, które podzielą
podkowę na sześć części w taki sposób, że każda
część będzie miała jeden otwór.
Rozwiązanie pod koniec wykładu.
7
8. Reguła #3
Dokładne obliczenia i rozumowanie będąbardziej konstruktywne, jeśli zbudujesz
model dla danego problemu, definiując
jego zmienne, ograniczenia i cele.
9. Zagadka 3.1
• Pewne przedsiębiorstwo produkcyjne ma w ofercietylko dwa produkty: krzesła i stoły.
– zysk ze sprzedaży krzesła wynosi 20$.
– zysk ze sprzedaży stołu 30$.
• Wyprodukowanie krzesła wymaga jednej sztuki drewna
i trzech roboczogodzin, zaś wyprodukowanie stołu
wymaga sześciu sztuk drewna i jednej roboczogodziny.
• Proces produkcji ma pewne ograniczenia:
• W procesie produkcyjnym mamy pewne ograniczenia:
wszystkie maszyny mogą przetworzyć
288 sztuk drewna dziennie, a liczba dostępnych
każdego dnia roboczogodzin wynosi 99.
9
10. Zagadka 3.1
• Pytanie brzmi:ile krzeseł i stołów powinna produkować
firma, aby jej zysk był maksymalny?
• Zacznijmy od zbudowania modelu…
10
11. Zagadka 3.1
• Stosując regułę #3, możemy skonstruować modelproblemu, określając następujące jego elementy:
• Zmienne: są tylko dwie zmienne, x i y odpowiadające
liczbie produkowanych krzeseł i stołów.
• Ograniczenia: są dwa ograniczenia produkcji na dobę:
– 288 przetważanych jednostek drewna
– 99 roboczogodzin.
• Cele: w tym konkretnym przypadku jedynym celem jest
maksymalizacja zysku.
11
12. Zagadka 3.1
• Cel:• maksymalizacja wartości: 20$ x + 30$ y
• Np. jeśli firma będzie produkowała 10 krzeseł (x = 10) i
15 stołów (y = 15) dzienny zysk będzie wynosił:
20$ × 10 + 30$ × 15 = 200$ + 450$ = 650$.
• Oczywiście im więcej wyprodukujemy krzeseł i stołów
tym zysk będzie większy, np. jeżeli zamiast 15
wyprodukujemy 20 stołów (tj. y = 20), to dzienny zysk
będzie wynosił:
20$ × 10 + 30$ × 20 = 200$ + 600$ = 800$.
12
13. Zagadka 3.1
• Ograniczenia:– wyprodukowanie krzesła wymaga jednej sztuki drewna i
trzech roboczogodzin
– wyprodukowanie stołu wymaga sześciu sztuk drewna
i jednej roboczogodziny
– wszystkie maszyny mogą przetworzyć 288 sztuk drewna
dziennie
x + 6y ≤ 288 (drewno)
– liczba dostępnych każdego dnia roboczogodzin wynosi 99.
3x + y ≤ 99 (praca)
13
14. Zagadka 3.1
• Model:• formalny, matematyczny model zadania maksymalizacji
zysku przedsiębiorstwa może być sformułowany
następująco:
• maksymalizacja wartości: 20$ x + 30$ y
• Przy ograniczeniach:
x + 6y ≤ 288
3x + y ≤ 99
gdzie x ≥ 0 i y ≥ 0 i gdzie wartości obydwu zmiennych
mogą przyjmować wyłącznie wartości całkowite.
14
15. Zagadka 3.1
• Rozwiązanie:• może to nie takie oczywiste na pierwszy rzut oka,
ale…
x = 18 i y = 45
co daje zysk w wysokości 1710$.
• To najlepszy plan jaki możemy przyjąć – każda inna
para liczb (inna liczba krzeseł i stołów) da mniejszy
zysk.
Dojście do rozwiązania na kolejnych wykładach.
15
16. Zagadka 3.1
• Jednak przy rozwiązywaniu tego typu zadaniazawsze należy sobie zadać dodatkowe pytania:
– Czy ten model jest adekwatny do postawionego
problemu?
– Czy zawarliśmy w nim wszelką istotną informację?
Zawsze można stworzyć więcej niż jeden model dla
problemów świata rzeczywistego.
16
17. Mapa – model świata rzeczywistego
• Weźmy „idealną” mapę dla dowolnego dużegomiasta (mapa – model świata rzeczywistego),
jaka może być przydatna do różnego rodzaju
zadań planowania trasy w tym mieście.
17
18. Mapa – model świata rzeczywistego
1819. Dobry model
• Dobry model – dostatecznie dokładny, abywygenerować sensowne, konkretne rozwiązania,
ale z drugiej strony – niezbyt złożony, aby nie
okazał się zbyt trudnym do użycia.
• Dobry model powinien spełniać dwa intuicyjne
wymagania:
– powinien być na tyle ogólny, aby informacje i cechy
nieistotne dla rozwiązania problemu zostały zakryte
– powinien być na tyle szczegółowy, aby mógł dać
sensowne rozwiązanie.
19
20. Model – kwestie do rozważenia
• Jak dokładny jest model (oceniając w ramach pojęćświata rzeczywistego, który modeluje)?
• Jak trudno jest znaleźć rozwiązanie w przyjętym
modelu?
• Jak oceniany jest kompromis między precyzją modelu,
a jakością i przydatnością zwracanych rozwiązań?
• Jak często model będzie używany?
• Ile czasu zajmuje przeciętnie znalezienie rozwiązania?
• Jaki jest koszt zastosowania znalezionego rozwiązania?
20
21. Krzesła i stoły
• Czy ten model dałoby się zastosować wświecie rzeczywistym?
• maksymalizacja wartości: 20$ x + 30$ y
• Przy ograniczeniach:
x + 6y ≤ 288
3x + y ≤ 99
gdzie x ≥ 0 i y ≥ 0 i gdzie wartości obydwu zmiennych mogą
przyjmować wyłącznie wartości całkowite.
21
22. Zagadka 3.4
• Pani Brązowa obchodziła urodziny i jeden zgości zapytał ją o jej wiek. Pani Brązowa
odpowiedziała, że suma jej wieku i wieku jej
męża, pana Brązowego, wynosi 140, a
następnie dodała: „Mój mąż ma dwa razy tyle
lat, co ja miałam, kiedy mój mąż miał tyle lat,
co ja teraz”.
• Ile lat ma pani Brązowa?
22
23. Zagadka 3.4
x: wiek pani Brązowej,y: wiek pana Brązowego
Suma wieku pani Brązowej i pana Brązowego wynosi 140:
x + y = 140
Pan Brązowy ma dwa razy tyle lat, ile miała pani Brązowa, kiedy
pan Brązowy miał tyle lat, co pani Brązowa teraz :
y>x
(y – x) lat temu pan Brązowy miał tyle lat, co pani Brązowa teraz
W tamtym czasie pani Brązowa miała x – (y – x) lat
y = 2(x – (y – x))
23
24. Zagadka 3.4
x: wiek Pani Brązowej,{
y: wiek Pana Brązowego
x + y = 140
y = 2(x – (y – x))
Łatwe rozwiązanie:
x = 60
y = 80
Pani Brązowa obchodziła sześćdziesiąte urodziny.
24
25. Obserwacja
• W 1579 François Viète zapoczątkowałużywanie symboli algebraicznych – x, y, z, etc.
– do oznaczania wartości nieznanych.
• Prosta, ponad 400-letnia idea, której nadal niektórzy nie
potrafią pojąć: niech x będzie wartością nieznaną, której
szukamy; zapisz warunki zadania w postaci równania z
niewiadomą x, a następnie rozwiąż je, tym samym
otrzymując szukaną wartość.
25
26. Pieniądze i procenty
• Jan odziedziczył po zmarłym stryju 25%procent więcej pieniędzy niż jego siostra Julia.
Zamierza oddać jej część otrzymanych
pieniędzy, tak aby obydwoje odziedziczyli
po tyle samo.
• Jaki procent swoich pieniędzy powinien Jan
przekazać siostrze?
26
27. Pieniądze i procenty
• Julia odziedziczyła x.• Jan odziedziczył 1.25 x.
• Powinien dać jej 0.125 x tak, aby obydwoje
mieli po 1.125 x.
• 0.125 x to 10% wartości 1.25 x, czyli Jan
powinien dać Julii 10% swojej części pieniędzy.
27
28. Znaczenie modeli w życiu codziennym
• Znacznie mniej osób obawia się wypadkusamochodowego niż ataku terrorystycznego.
Tymczasem w wypadkach samochodowych ginie
nieporównanie więcej osób niż w wyniku ataków
terrorystycznych.
Prosty model (statystyki z 1985, USA):
• 45,000 zabitych w wypadkach
samochodowych,
• 17 zabitych przez terrorystów.
28
29. Znaczenie modeli w życiu codziennym
• Prosty probabilistyczny model pozwolizobaczyć te dane z innej perspektywy. Mamy
następujące szanse:
1 : 1,600,000 – bycia zabitym przez terrorystę,
1 : 68,000 – zakrztuszenia się na śmierć,
1 : 75,000 – zgonu w wypadku rowerowym,
1 : 20,000 – utonięcia,
1 : 5,300 – zgonu w wypadku samochodowym
29
30. Znaczenie modeli w życiu codziennym
• Wiele osób nadinterpretowuje „niezwykłe” związki postaci:• Krzysztof Kolumb odkrył Nowy Świat w 1492 roku, a Włoch
Enrico Fermi odkrył nowy świat przestrzeni atomów w 1942 roku.
• Sekretarka prezydenta Kennedy’ego nazywała się Lincoln, natomiast
sekretarka prezydenta Lincolna nazywała się Kennedy.
• Każde słowo w imieniu Ronald Wilson Reagan (były prezydent USA)
ma 6 liter (stąd skojarzenie z “666”).
• Znany pisarz Mark Twain urodził się w 1835 roku, w dniu w którym pojawiła
się na niebie kometa Halleya, a zmarł w 1910 roku, w dniu ponownego
pojawienia się komety w pobliżu Ziemi.
• Życia Thomasa Jeffersona i Johna Adamsa, dwóch ojców-założycieli Stanów
Zjednoczonych, którzy mieli wielki wkład w powstanie
i podpisanie Deklaracji Niepodległości 4 lipca 1776 roku, zakończyły się w tym
samym dniu. Obaj zmarli 4 lipca 1826 roku, dokładnie w 50 lat po podpisaniu
najważniejszego dokumentu w dziejach USA.
30
31. Znaczenie modeli w życiu codziennym
• Proste modele mogą nas chronić przed tendencjądo drastycznego niedoceniania częstości
występowania zbiegów okoliczności wokół nas i
nadawania takim „niezwykłym” sytuacjom
znaczenia magicznego…
• Ilu z nas miało jakąś ciocię, babcię lub kuzynkę,
której przyśnił się poważny wypadek
samochodowy z udziałem przyjaciela lub
bliskiego krewnego, a kilka godzin później taki
wypadek faktycznie się zdarzył?
31
32. Znaczenie modeli w życiu codziennym
• Zbudujmy prosty model.• Załóżmy, że prawdopodobieństwo tzw. proroczego snu
wynosi 1:10000.
• Oznacza to, że takie zdarzenie jest niezwykle rzadkie –
szanse na „nieproroczy” sen są jak 9999 do 10000.
• Ponadto przyjmijmy, ze sny są zdarzeniami niezależnymi,
tzn. że wystąpienie bądź nie snu proroczego jednego nie
dnia, nie ma żadnego wpływu na wystąpienie bądź nie snu
proroczego następnego dnia.
• Te założenia są ważne dla modelu, który zamierzamy
zbudować.
• A teraz policzmy…
32
33. Znaczenie modeli w życiu codziennym
• Prawdopodobieństwo wyśnienia jednego „nieproroczego”snu wynosi:
0.9999
• Prawdopodobieństwo wyśnienia dwóch kolejnych
„nieprorocznych” snów wynosi:
0.9999 × 0.9999
• Prawdopodobieństwo wyśnienia trzech kolejnych
„nieprorocznych” snów wynosi:
0.9999 × 0.9999 × 0.9999
(zasada mnożenia prawdopodobieństw zdarzeń niezależnych)
33
34. Znaczenie modeli w życiu codziennym
• Prawdopodobieństwo wyśnienia n „nieproroczych” snówwynosi:
0.9999n
• Jeżeli ktoś miewa sny każdej nocy, to prawdopodobieństwo
wyśnienia n = 365 „nieproroczych” snów (całego roku bez
proroczych snów) wynosi:
0.9999365 ≈ 0.964
• Wniosek 1: Około 96.4% ludzi, którzy śnią każdej nocy, nie
będzie miało żadnego proroczego snu przez cały rok.
34
35. Znaczenie modeli w życiu codziennym
• Wniosek 2: Około 3.6% ludzi, którzy śnią każdej nocy,będzie miało w ciągu roku przynajmniej jeden proroczy
sen.
3.6% przekłada się na miliony ludzi na świecie…
• Zwróćmy też uwagę, że nawet zmniejszając
prawdopodobieństwo wystąpienia proroczego snu do
poziomu 1 : 1000 000, liczba osób, którym proroczy sen
może się przytrafić jest nadal całkiem pokaźna.
35
36. Znaczenie modeli w życiu codziennym
• Zbiegi okoliczności zdarzają się na świecie dużoczęściej, niż wydaje się to wielu osobom.
• Kluczowa umiejętność: odróżnianie zdarzeń
specyficznych od powszechnych.
• Jakie jest prawdopodobieństwo, że w grupie słuchaczy
są dwie osoby, które mają urodziny tego samego dnia?
• Jakie jest prawdopodobieństwo, że w gupie jest druga
osoba, która obchodzi urodziny 24 stycznia?
36
37. Znaczenie modeli w życiu codziennym
• Kluczowa umiejętność: odróżnianie zdarzeńspecyficznych od powszechnych.
• Jeżeli mamy koło (a la koło fortuny) z namalowanymi
26 literami i zakręcimy nim 100 razy, to
prawdopodobieństwo, że w powstałej sekwencji
ułoży się słowo PIES albo KOT jest raczej niewielkie.
Ale prawdopodobieństwo, że ułoży się jakiekolwiek
słowo jest już dość spore.
37
38. Znaczenie modeli w życiu codziennym
Przykład:• Sekwencja pierwszych liter nazw kolejnych
miesięcy – w języku angielskim:
JFMAMJJASOND
38
39. Znaczenie modeli w życiu codziennym
Przykład:• Sekwencja pierwszych liter nazw kolejnych
miesięcy – w języku angielskim:
JFMAMJJASOND
39
40. Znaczenie modeli w życiu codziennym
Przykład:• Sekwencja pierwszych liter nazw kolejnych
miesięcy – w języku angielskim:
JFMAMJJASOND
• Sekwencja pierwszych liter nazw planet
– w języku angielskim:
MVEMJSUNP
40
41. Znaczenie modeli w życiu codziennym
Przykład:• Sekwencja pierwszych liter nazw kolejnych
miesięcy – w języku angielskim:
JFMAMJJASOND
• Sekwencja pierwszych liter nazw planet
– w języku angielskim:
MVEMJSUNP
41
42. Znaczenie modeli w życiu codziennym
• Inny (pouczający) przykład…• Jeden z przyjaciół Zygmunta Freuda, Wilhelm
Fliess (chirurg) wymyślił i w 1897 roku ogłosił
teorię biorytmów – metodę oceny kondycji
osoby opartą na założeniu, że różne aspekty
ludzkiego życia podlegają ustalonym,
okresowym cyklom, które rozpoczynają się
w chwili narodzin.
42
43. Znaczenie modeli w życiu codziennym
• Fliess uważał, że dwie liczby 23 i 28reprezentują długości takich cykli,
odpowiednio dla mężczyzn i kobiet.
• Zauważył on, że te dwie liczby, 23 i 28, mają
„szczególną” własność: dodanie do siebie ich
wielokrotności pozwala na uzyskanie dowolnej
liczby całkowitej, np.:
21 = 7 × 23 + ( 5 × 28)
43
44. Znaczenie modeli w życiu codziennym
• Freud był pod tak wielkim wrażeniem tegoodkrycia, że nie tylko mocno wspierał
popularyzację teorii biorytmów, ale również był
przekonany, że umrze w wieku 51 lat (suma 23 i
28).
• Fakt: tę „szczególną” własność mają dwie
dowolne liczby względnie pierwsze (np. 21 i 25)…
A Freud zmarł w wieku 83 lat…
44
45. Pamiętaj o regule #3
Dokładne obliczenia i rozumowanie będąbardziej konstruktywne, jeśli zbudujesz
model dla danego problemu, definiując
jego zmienne, ograniczenia i cele.
46. Praca domowa #3a
• Cena biletu do parku rozrywki została obniżona; wrezultacie park odnotował 50-procentowy wzrost
liczby odwiedzających. W tym samym czasie zyski
ze sprzedaży biletów wzrosły o 20%.
O jaki procent została zredukowana cena biletu?
• Zbuduj model tego problemu, wskaż istotne
zmienne i podaj równania, które doprowadzą do
rozwiązania.
46
47. Praca domowa #3b
• Abacki, Babacki i Cabacki postanowili we własnym gronierozegrać zawody lekkoatletyczne. Było kilka dyscyplin, w
których startowali i w każdym z przypadków zwycięzca
otrzymywał g punktów, drugi – s punktów, a ostatni, tj.
trzeci – b punktów. Oczywiście g > s > b > 0. Ustalono też,
że wszystkie trzy wartości: g, s i b są liczbami całkowitymi.
• Zawody zakończyły się i w żadnej z dyscyplin nie było
remisów. Abacki zdobył 22 punkty, natomiast Babacki i
Cabacki zebrali po 9 punktów każdy. Babacki wygrał skok w
dal.
Kto był drugi w wyścigu na 400 metrów?
• Zbuduj model tego problemu, wskaż istotne zmienne i
podaj równania, które doprowadzą do rozwiązania.
47
48. Zagadka 3.2
• Stoisz przy drzwiach, prowadzących do pustego pokoju,w którym u sufitu wiszą trzy żarówki. Wszystkie trzy
żarówki są wyłączone. Na zewnętrznej ścianie pokoju,
przy drzwiach są trzy przełączniki, z których każdy
włącza i wyłącza inną żarówką (zatem między każdym
przełącznikiem a każdą żarówką jest związek jeden do
jednego). Wszystkie trzy przełączniki są ustawione w
pozycji „wyłączony”. Twoim zadaniem jest ustalenie,
którym przełącznikiem włącza się którą żarówkę.
48
49. Zagadka 3.2
• Rozwiązanie: wzbogacenie standardowegomodelu (włączony/wyłączony) o czynnik
temperatury!
• Ustawiamy dwa przełączniki (np. A i B) w
pozycji „włączony”, pozostawiając trzeci
przełącznik (tzn. C) w pozycji „wyłączony”.
Czekamy 5 minut, ustawiamy przełącznik A w
pozycji „wyłączony” i wchodzimy do pokoju.
49
50. Zagadka 3.3
• Jest sobie podkowa z sześcioma otworami nagwoździe:
• Wykonaj dwa prostoliniowe cięcia, które podzielą
podkowę na sześć części w taki sposób, że każda
część będzie miała jeden otwór.
50
51. Zagadka 3.3
Rozwiązanie:Cięcie 1
Cięcie 2
51

















































 psychology
psychology