Similar presentations:
Основи випромінювання електромагнітних хвиль
1. Розділ 7 ОСНОВИ ВИПРОМІНЮВАННЯ ЕЛЕКТРОМАГНІТНИХ ХВИЛЬ
LOGO1
2. Зміст
Add your company sloganЕлементарний електричний випромінювач
7.1 (диполь Герца, електричний вібратор)
7.2 Магнітний елементарний випромінювач
7.3 Елементарний щілинний випромінювач
7.4 Елемент Гюйгенса
7.5 Висновки
7.5
7.6 Контрольні питання та завдання
LOGO
2
3. 7.1Елементарний електричний випромінювач (диполь Герца, електричний вібратор) 7.1.1 Загальні положення
Add your company slogan7.1Елементарний електричний випромінювач (диполь Герца,
електричний вібратор)
7.1.1 Загальні положення
Як випромінювач, Герц використовував
вібратор з іскровим проміжком, який збуджує
коливання (диполь Герца).
Довжина цього вібратора значно менша
довжини хвилі ( l ), тому значення сили та
фази вздовж всієї довжини випромінювача
однакові.
Тобто диполь Герца – це короткий, в
порівнянні з довжиною хвилі, вібратор, й
можна вважати, що відстань від точки
спостереження до будь-якої точки диполю
однакова. Умовно можна вважати, що заряди
скоцентровані на кінцях стрижня, тому його й
називають диполем. Теорія сучасних антен
створена на основі цього пристрою.
Рисунок 7.1 - Складники електромагнітного поля диполя Герца
Визначимо формули, які описують вектори і у довільній точці простору. Будемо вважати, що вібратор збуджують
гармонічним сигналом. Нехай диполь Герца розташований відносно декартової системи координат. Напруженість
поля в будь-якій точці простору може бути визначена за таким алгоритмом: . З’ясуємо докладніше.
LOGO
3
4.
Add your company sloganLOGO
4
5.
Add your company sloganЗа значенням густини струму визначаємо з урахуванням, що векторний потенціал є таким, що запізнюється
(або в комплексній формі (для гармонічного сигналу):
Вектор визначимо через векторний потенціал:
A
4
V
r
J t
v
dV
r
Am
4
(7.1)
J m e j r
r dV
(7.1а)
Електричне поле знайдемо з першого рівняння Максвелла для діелектричного середовища:
Hm
1
rot Am
(7.2)
Оскільки об'єм , що охоплений струмом малий, густина струму всередині цього об'єму – величина незмінна.
Згадаємо, що , тобто відстань від довільної точки вібратора до довільної точки простору – точки спостереження,
теж величина незмінна. Тому рівняння надамо у вигляді
rotH
.
E
1
rot H m j E m E m j
rot H m
t
(7.3)
Вібратор скеровано вздовж осі Z. Тому:
Am
4
0,
.
I m le j r
4
r
V
J m e j r
dV
r
4
V
J m e j r
dS dl
r
4
l
I m e j r
dl
r
(7.1б)
Amx 0,
Amy
Amz
(7.4)
LOGO
5
6.
Add your company slogan;
Задачу розв'язуємо за допомогою вектора
I m le j r
Радіальна складова: Amr Amz cos
cos
4 r
I le j r
sin
Меридіальна складова: Am Amz sin m
4 r
.
Am Amr 1r Am 1 Am 1
(7.5)
(7.5а)
Азимутна складова: Am 0
Внаслідок колової симетрії вібратора
(7.5б)
Amr
0 Am 0
1 (r Am ) Amr
H m 1 H m 1
.
r r
Тобто випливає, що напруженість магнітного поля має тільки азимутну складову H
H m
I m l re j r
sin
4 r r r
I m l 2e j r
4
e j r
I m l
1
j r I m l 1 j r
cos
sin
j sin sin e
j e
r
4 r r 2
r
4 r
2
1
1
I m l 2 j r
j
sin
e
j
sin .
2 2
4
2
r
2
r
r r
(7.6)
LOGO
6
7.
В сферичній системі координат:Em
1
1
j
1r
r sin
1 1
1
r sin
E mr
E m
E m 0
E m
I m lZ w 2e j r
4
H
mr
Add your company slogan
H m sin
H m
r H m
r H m
1
H
mr
1
r
r
r
.
(7.7)
H m sin
1
.
j
r sin
(7.8)
r H m
r H m
1
1
ej2 ;
j
r
r
r
r
(7.9)
2
j
2
r
2
r
j
2 r
3
sin
(7.10)
Випливає, що в залежності від співвідношення між довжиною хвилі та відстанню від диполя до довільної точки у
просторі їх можна спростити, якщо умовно поділити простір зайнятий полем на дві області (зони): ближню зону
(зона індукції) й дальню зону (зона випромінювання) за ознаками:
якщо: r - ближня зона,
2
(7.11)
(7.11а)
якщо : r
- дальня зона.
2
LOGO
7
8. 7.1.2 Ближня зона (зона індукції)
Add your company slogan7.1.2 Ближня зона (зона індукції)
.
В ближній зоні r rгр 2
1
2 r
Тобто у виразах доданками
2 r
H m
n
з меншими степенями n можна знехтувати
I m l 2
2
Iml
sin
sin .
2 2
4 2 r
4 r 2
2
(7.12)
j
I ml 2
I ml
I ml
3
2
cos
j
cos
e
cos .
3 3
3
3
2 2 r
2 r
2 r
3
Emr j
j
I ml 2
I ml
I ml
2
sin
j
sin
e
sin .
4 2 r
4 r 3
4 r 3
У ближній зоні напруженість магнітного поля є в фазі зі струмом.
3
(7.13)
3
Em j
(7.14)
В ближній зоні відбувається обмін енергією між електричним та магнітним полями, тому цю зону ще називають
зоною коливань або зоною індукції.
Визначимо коефіцієнт пропорційності між складовими E та H в ближній зоні:
I m l sin 4 r 2
j
1
Z бз
j
,
3
4 r
sin
r j r
H m
Iml
1
Z бзE
(7.16)
r
E
E m
(7.15)
LOGO
8
9.
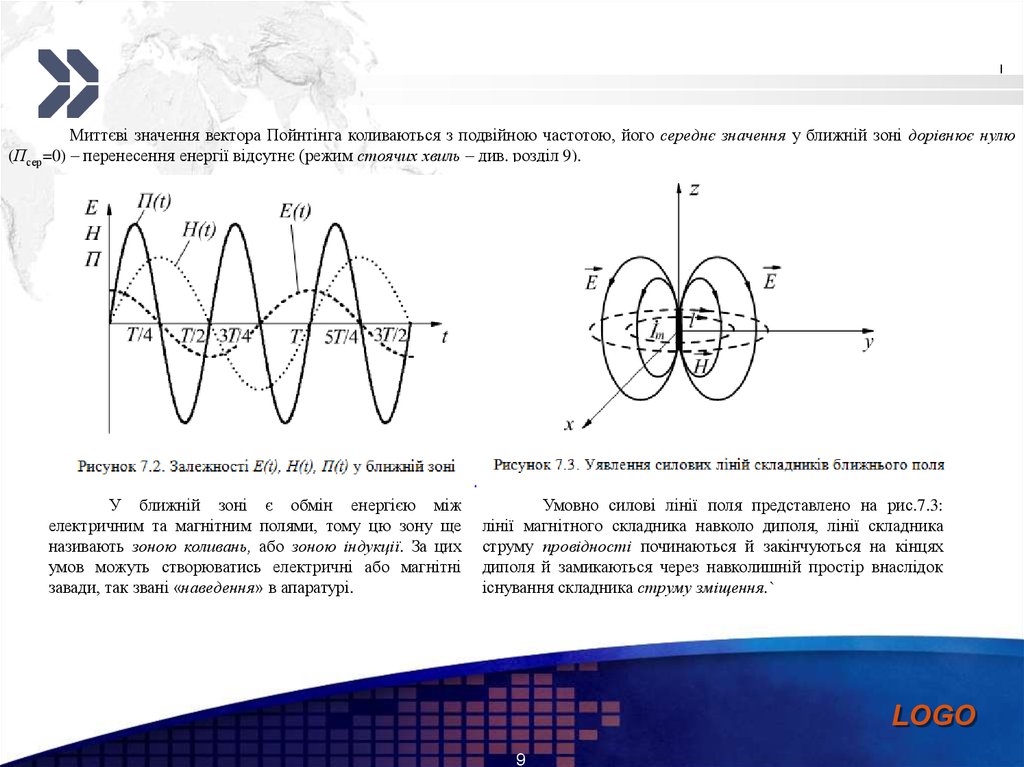
Add your company sloganМиттєві значення вектора Пойнтінга коливаються з подвійною частотою, його середнє значення у ближній зоні дорівнює нулю
(Псер=0) – перенесення енергії відсутнє (режим стоячих хвиль – див. розділ 9).
У ближній зоні є обмін енергією між
електричним та магнітним полями, тому цю зону ще
називають зоною коливань, або зоною індукції. За цих
умов можуть створюватись електричні або магнітні
завади, так звані «наведення» в апаратурі.
Умовно силові лінії поля представлено на рис.7.3:
лінії магнітного складника навколо диполя, лінії складника
струму провідності починаються й закінчуються на кінцях
диполя й замикаються через навколишній простір внаслідок
існування складника струму зміщення.`
LOGO
9
10.
Add your company sloganLOGO
10
11. 7.1.3 Дальня зона (зона випромінення)
Add your company slogan7.1.3 Дальня зона (зона випромінення)
.
,
Як вже зазначено в дальній зоні r
тобто 2 r 1
2
n
j r
В такій ситуації доданками 2 r з більшими степенями n можна знехтувати, а запізнення, яке відображає множник e
слід враховувати.
Тоді вирази для складових електромагнітного поля в дальній зоні матимуть вигляд:
I m l e j r
j
sin
4 r
H m
(7.17)
E m
I m l 2e j r
j
sin
4 r
E mr
(7.18)
I m l e j r
cos
2 r 2
(7.18а)
середнє значення вектора Пойнтінга cep 0 , отже, в дальній зоні існує процес перенесення електромагнітної енергії.
Визначимо хвильовий імпеданс:
E
j I m l 2 sin 4 r
1
Z дзE m
H m
f
j I m l sin 4 r
(7.19)
9
7
У вільному просторі 0 4 10 Гн / м, 0 1 / 36 10 Ф / м
Z wE0 120 377Ом
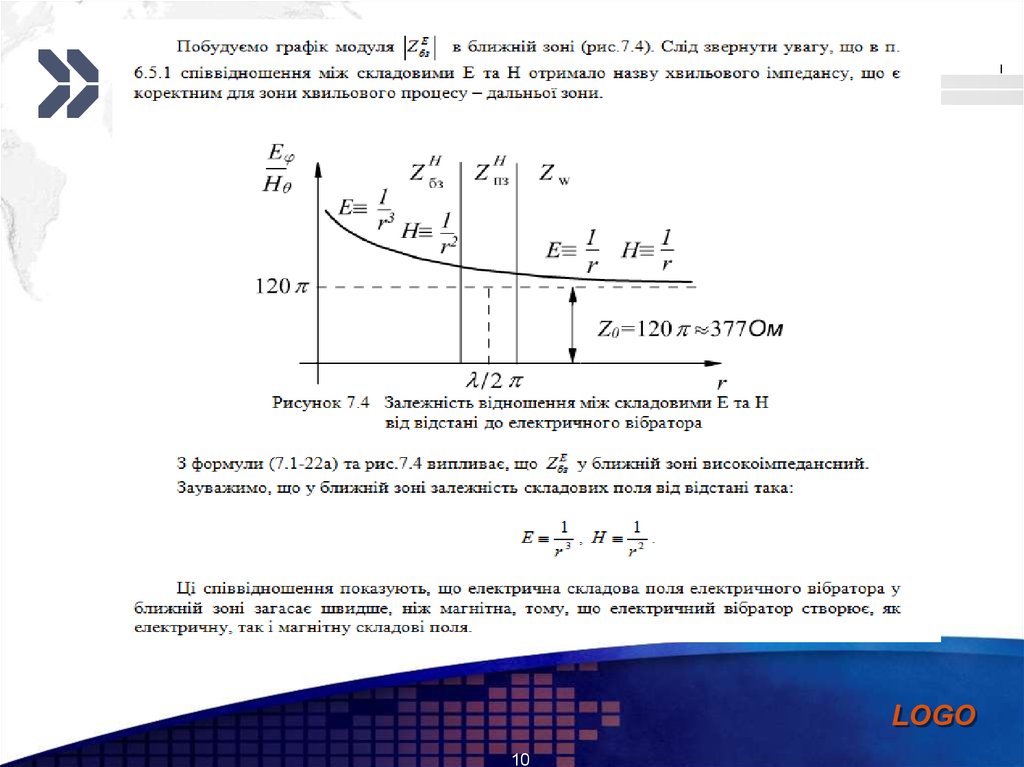
Зауважимо, що у дальній зоні виконуються такі співвідношення:
1
1
E
H
r
r
LOGO
11
12.
Add your company sloganLOGO
12
13. 7.1.4 Проміжна зона
Add your company sloganОзнакою цієї зони є те, що поле випромінювання, дальнє, та реактивне (зв'язуюче), ближнє поле
характеризуються значеннями однакового порядку.
Рисунок 7.7 - Стадії формування електромагнітного
поля: а-д силові лінії; е-к часові діаграми струму в
диполі
LOGO
13
14.
Add your company sloganУмовно для диполя Герца лінії електричного поля представлені таким чином:
Рисунок 7.8 – Силові лінії складових поля: а – магнітного ; б – електричного
LOGO
14
15. 7.1.5. Діаграма спрямованості випромінювача
Add your company slogan7.1.5. Діаграма спрямованості випромінювача
В загальному випадку діаграма спрямованості – це геометричне місце точок
однакового
значення фізичної величини, в залежності від напряму. В курсі “Технічна електродинаміка” цьому
терміну надано такий зміст.
Діаграма спрямованості – це графічне зображення залежності амплітуд векторів поля
випромінювання в дальній зоні від кута спостереження.
Випромінювач, електричний вібратор, не випромінює електромагнітне поле вздовж своєї осі, а
вздовж осі перпендикулярній до осі вібратора випромінення максимальне. Відповідно до можна
записати в меридіанній площині Em Emax sin
В азимутальній площині для складової H – діаграма спрямованості – круг Введемо безрозмірну функцію –
нормовану характеристику, що визначає діаграму спрямованості в меридіанній площині:
F ( , )
Em
sin
Emax
(7.20)
Побудуємо її об'ємне графічне зображення, що має назву нормованої діаграми спрямованості. Оскільки в
горизонтальній площині Em не залежить від , то діаграма має вигляд тороїда
LOGO
15
16.
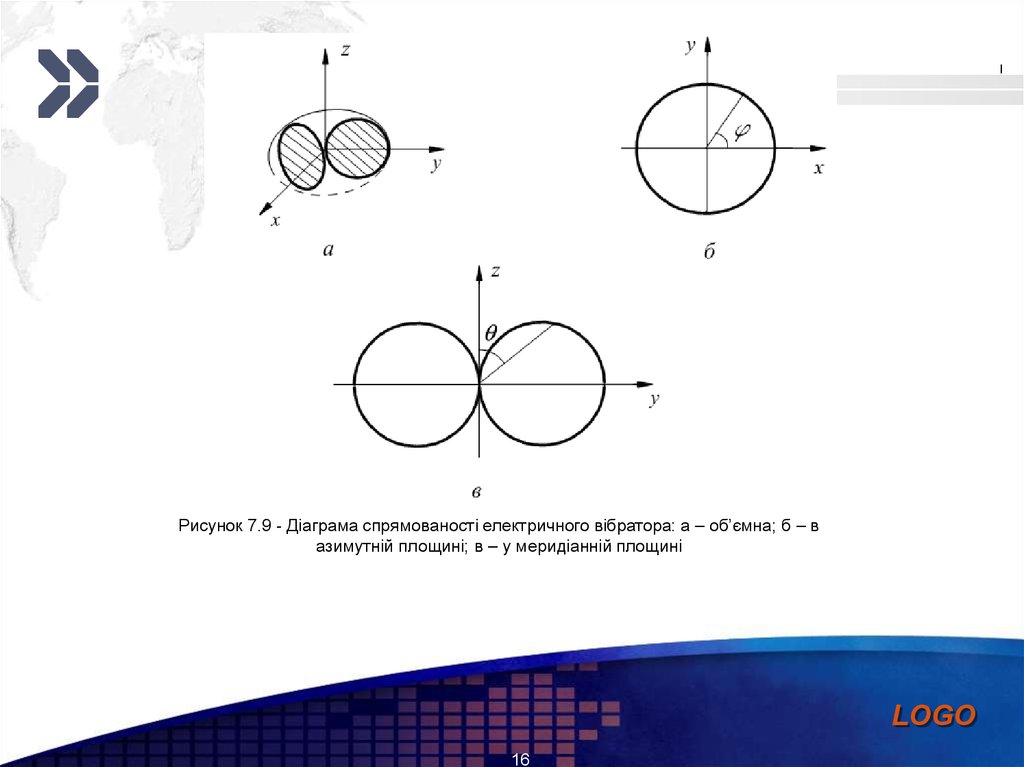
Add your company sloganРисунок 7.9 - Діаграма спрямованості електричного вібратора: а – об’ємна; б – в
азимутній площині; в – у меридіанній площині
LOGO
16
17.
Add your company sloganРисунок 7.10 – Діаграма спрямованості диполя Герца
LOGO
17
18. 7.1.6. Потужність та опір випромінювання диполя Герца
Add your company slogan7.1.6. Потужність та опір випромінювання
диполя Герца
Як вже відомо, потужність хвильового процесу визначють інтегруванням вектора Пойнтінга:
Розглянемо детальніше вектор Пойнтінга і потужність випромінювання.
( I m l )2
1
2
Re E H
Z w sin 1r
2 2
2
8r
Пcep
P Псер dS
sin
s
d
0
2
P
3
0 0
P П dS
(7.21)
S
dS r 2 sin d d
(7.22)
(7.23)
4
3
(7.24)
(7.25)
( I m l )2 sin 3 Z w
Z w ( I ml ) 2
d d
8 2
3 2
I m2 R
На підставі виразу для електричної потужності, можна записати: P
2
R
де - опір випромінювання.
2 Z w l
2P
R 2
3
Im
2
Хвильовий імпеданс у вільному просторі Z w
l
R 80
(7.26)
0
120
0
2
2
(7.27)
LOGO
18
19. 7.2. Магнітний елементарний випромінювач 7.2.1. Метод вирішення задач
Add your company slogan7.2. Магнітний елементарний випромінювач
7.2.1. Метод вирішення задач
Поле, що утворює елементарний магнітний випромінювач, можна дослідити за методикою аналогічною
електричному диполю. Елементарний магнітний випромінювач створимо як аналог електричного вібратора але з
магнітним струмом ІM.
Тобто можливо на підставі принципу переставної двоїстості виконати відповідні заміни:
(7.28)
H E I I
E H
E H
r
М
r
На показано електричний вібратор Герца, але з магнітним струмом ІM, який створює силові лінії електромагнітного
поля.
Рисунок 7.11- Елементарний магнітний випромінювач: а – з фіктивним магнітним
струмом ІM; б – з реальним електричним струмом (рамка зі струмом)
LOGO
19
20.
Add your company sloganТаким чином систему рівнянь складових електромагнітного поля магнітного елементарного випромінювача для
загального вигляду можна отримати для складових електромагнітного поля , E H r H , на підставі заміни таким
чином:
2
I mM l 2 j r
E m
e j
sin ,
(7.29)
2 r 2 r
4
H mr
I
l 3e j r
mM
2
H m
I l 3e j r
mM
4
3
2
j
cos ,
2 r
2 r
2
j
2 r 2 r
j
2 r
3
(7.30)
sin .
(7.31)
В природі магнітний струм не існує, тому реальний магнітний елементарний випромінювач – це рамка з
електричним струмом.
I
mM
Для отримання відповідних формул необхідно виконати заміну фіктивного магнітного
струму
в лінійному вібраторі
I
довжиною , реальним електричним струмом m в рамці площею S, тобто I mM l j I m S .
(7.32)
Враховуючи перепишемо рівняння складових електромагнітного поля магнітного елементарного випромінювача для
електричного струму:
2
j I m S 2 j r
(7.33)
E m
e j
sin ,
2 r 2 r
4
2
3
3 j r
(7.34)
j I m S e
H mr
j
cos
,
2
2 r
2 r
H m
j I m S 3e j r
4
2
j
2 r 2 r
j
2 r
3
sin .
(7.35)
LOGO
20
21. 7.2.2. Ближня зона
Add your company slogan7.2.2. Ближня зона
Наведемо формули, що отримані на основі принципу „переставної двоїстості”, за умов ближньої зони r 2
E
Визначимо співвідношення
H
(7.36)
(7.39)
(7.37)
(7.40)
(7.38)
(7.41)
H
для магнітного випромінювача: Z бз
E m
j r (7.42)
H
Z бз r
(7.43)
H m
H
Параметр Z бз електромагнітного випромінювача низькоімпедансний.
Рисунок 7.12 - Залежність відношення між складовими E та H
від відстані до магнітного випромінювача
LOGO
21
22. 7.2.3. Дальня зона
Add your company slogan7.2.3. Дальня зона
Наведемо формули, які отримані на основі принципу „переставної двоїстості” за умови дальньої зони r 2
Визначимо хвильовий опір
Zw
E
H
(7.43)
(7.46)
(7.44)
(7.47)
(7.45)
(7.48)
LOGO
22
23. 7.2.4. Потужність та опір випромінювання елементарного магнітного випромінювача
Add your company slogan7.2.4. Потужність та опір випромінювання
елементарного магнітного випромінювача
(7.49)
(7.50)
LOGO
23
24. 7.3. Елементарний щілинний випромінювач 7.3.1. Метод вирішення задач
Add your company slogan7.3. Елементарний щілинний випромінювач
7.3.1. Метод вирішення задач
Поряд з розглянутими раніше диполем Герца та магнітним елементарним випромінювачем існує, так званий,
елементарний щілинний випромінювач. Ця випромінююча система є бескінечною ідеально провідною площиною,
в якій прорізано щілину довжиною l та шириною
Рисунок 7.13 - Елементарний щілинний випромінювач.
LOGO
24
25.
Add your company slogan(7.51)
(7.52)
(7.53)
(7.54)
(7.55)
LOGO
25
26. 7.3.2 Потужність та опір випромінювання елементарного щілинного випромінювача
Add your company slogan7.3.2 Потужність та опір випромінювання
елементарного щілинного випромінювача
Усереднений за період коливальний вектор Пойнтінга має єдину складову, направлену по радіальному орту:
2
U Щm
(l ) 2 sin 2
1
Псрr E H
(7.56)
2
8 2 r 2 Z w
Потужність, що випромінюється елементарним щілинним вібратором, знаходимо шляхом інтегрування Псрr по поверхні S
сфери достатньо великого радіуса, точки якої розміщені в дальній зоні випромінювача:
P Псрr dS
S
2
U Щm
(l )2
8 2 Z w
2
0
0
3
d sin d
2
U Щm
(l )2
3 Z w
(7.57)
Оскільки потужність випромінювання є пропорційною квадрату напруги в щілині, то:
P
де R Щ
2
UЩ
m
(7.58)
2RЩ
- величина, що вимірюється в омах і називається опором випромінювання щілинного випромінювача.
RЩ
3 Z w
45( )2
2
2(l )
l
(7.59)
LOGO
26
27. 7.4 Елемент Гюйгенса
Add your company slogan(7.60)
LOGO
27
28.
Add your company sloganОкремі точки характеристик наведено у таблиці 7.3
Кути
cosθ
1+cosθ
0
1
2
π/2
0
1
π
-1
0
3π/2
0
1
Таблиця 7.3.Данні характеристики спрямованості елемента Гюйгенса
Рисунок 7.15 – Діаграма спрямованості елемента Гюйгенса
Рисунок 7.14 – До визначення елемента Гюйгенса
LOGO
28
29. 7.5. Висновки
Add your company sloganLOGO
29
30.
Add your company sloganLOGO
30
31. 7.6. Контрольні запитання та завдання
Add your company slogan7.6. Контрольні запитання та завдання
LOGO
31
32.
Add your company sloganLOGO
32





























 physics
physics








