Арифметические операции в системах счисления. (10 класс)

1. Ум заключается не только в знании, но и в умении прилагать знание в дело Аристотель

2. 1 – 10 2 - 5 3 - 4 4 - 1 5 - 2 6 - 8 7 - 3

1 – 10
2-5
3-4
4-1
5-2
6-8
7-3

3.

Укажите,
какие
числа
записаны
Какой
цифрой
заканчивается
четное
Какое
минимальное
основание
должна иметь
с ошибками
и аргументируйте
двоичное
число?
система
счисления,
если в ней ответ:
1237,быть
30064записаны
, 12ААС09
Какой
цифрой
заканчивается
нечетное
20, 13476
721, 201, 1201
могут
числа:
10,
двоичное число?

4. Арифметические операции в системах счисления

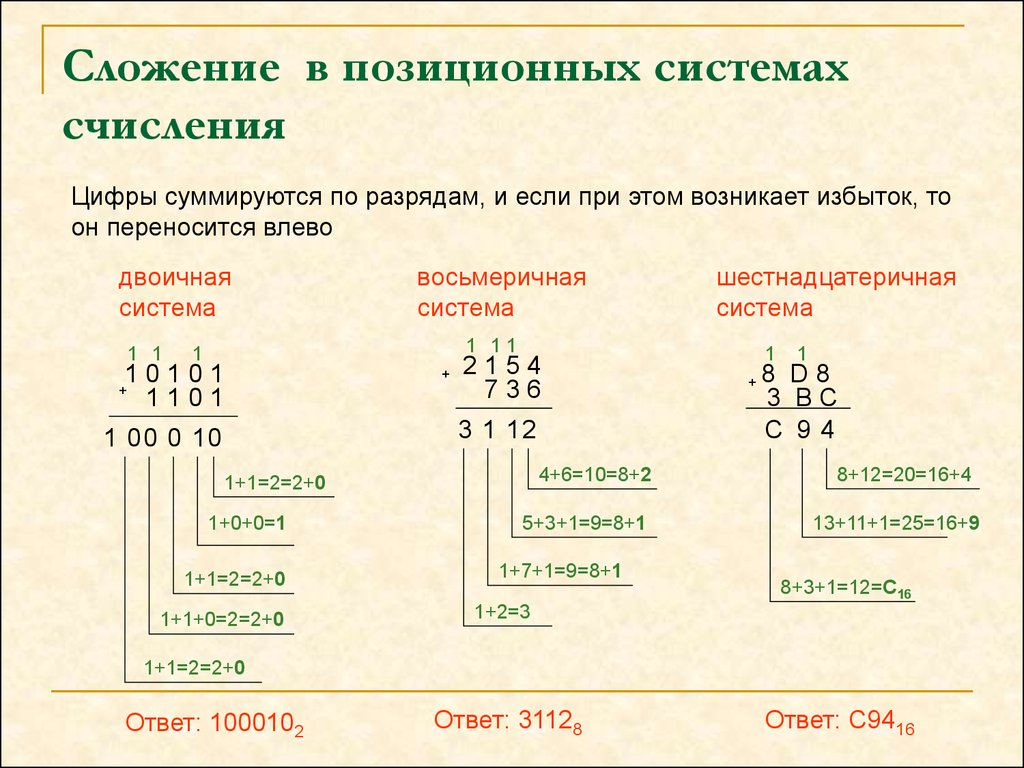
5. Сложение в позиционных системах счисления

Цифры суммируются по разрядам, и если при этом возникает избыток, то
он переносится влево
двоичная
система
1 1
восьмеричная
система
шестнадцатеричная
система
1 11
1
10101
1101
+
+
2154
736
3 1 12
1 00 0 10
4+6=10=8+2
1+1=2=2+0
1+0+0=1
1+1=2=2+0
1+1+0=2=2+0
5+3+1=9=8+1
1+7+1=9=8+1
1
+
1
8 D8
3 BC
C 94
8+12=20=16+4
13+11+1=25=16+9
8+3+1=12=C16
1+2=3
1+1=2=2+0
Ответ: 1000102
Ответ: 31128
Ответ: C9416

6.

Примеры:
1011012
+ 111112
1001100
1110112
+ 110112
1010110

7.

Примеры
3 5 38
+ 7 3 68
1311
1 3 5 38
+ 7 7 78
2352

8.

Пример:
С В А16
+ A 5 916
1713

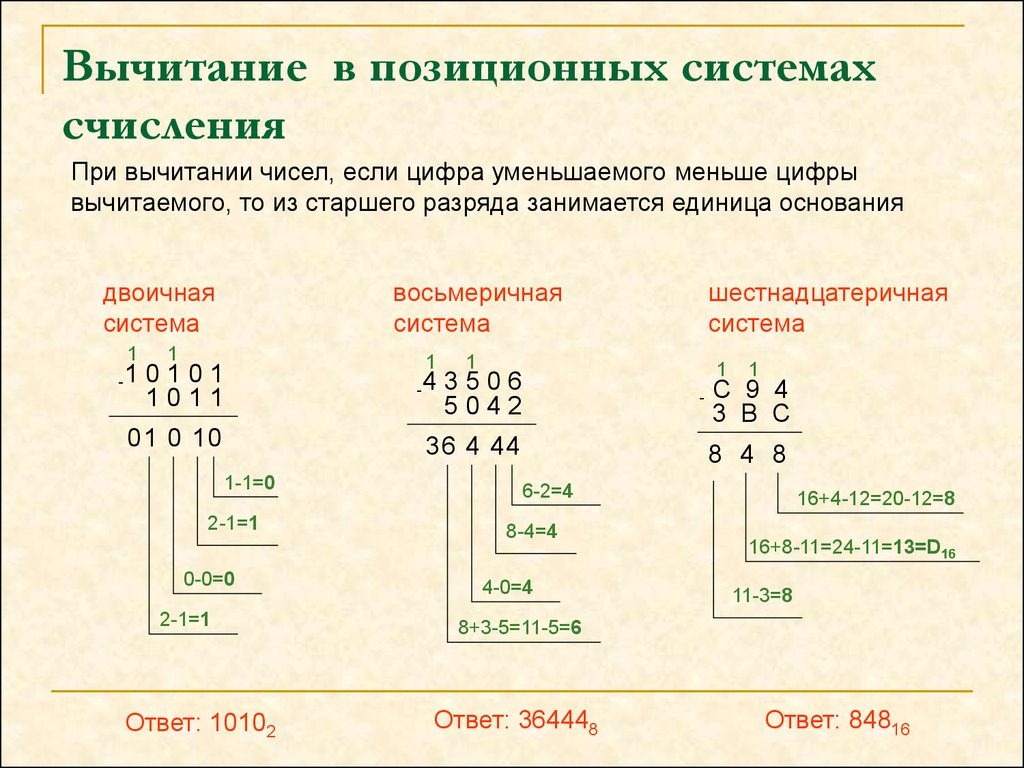
9. Вычитание в позиционных системах счисления

При вычитании чисел, если цифра уменьшаемого меньше цифры
вычитаемого, то из старшего разряда занимается единица основания
двоичная
система
1
восьмеричная
система
1
1
-1 0 1 0 1
1011
-
01 0 10
1
1
43506
5042
2-1=1
0-0=0
2-1=1
Ответ: 10102
1
- С 9 4
3 В С
36 4 44
1-1=0
шестнадцатеричная
система
8 4 8
6-2=4
8-4=4
4-0=4
16+4-12=20-12=8
16+8-11=24-11=13=D16
11-3=8
8+3-5=11-5=6
Ответ: 364448
Ответ: 84816

10.

Примеры:
1011012
– 111112
1110
1100112
– 101012
11110

11.

Примеры
–
6 6 28
1 5 68
504
1 1 5 68
– 6 6 28
274

12.

Пример:
А 5 916
– 1 В А16
89F

13. Умножение в позиционных системах счисления

При умножении многозначных чисел в различных позиционных системах
применяется алгоритм перемножения чисел в столбик, но при этом
результаты умножения и сложения записываются с учетом основания
системы счисления
двоичная
система
восьмеричная
система
2 2
4
1
х1
1011
1101
1
11011
1 1 1 0 1 1
11011
101011111
11
1+1+1=3=2+1
х
163
63
531
1262
3∙3=9=8+1
1 3 3 56∙3=18=16+2=8∙2+2
1
1
6∙3+1=19=16+3=2∙8+3
6∙6+2=38=32+6=4∙8+6
1∙3+2=5
6+5=11=8+3
6∙1+4=10=8+2
1+1+1=3=2+1
1+1=2=2+0
Ответ: 1010111112
Ответ: 133518

14. Деление в позиционных системах счисления

Деление в любой позиционной системе производится по тем же правилам,
как и деление углом в десятичной системе. При этом необходимо
учитывать основание системы счисления.
двоичная
система
восьмеричная
система
100011
1110
1110
1 0 ,1
1 11 0
1110
0
Ответ: 10,12
13351
1262
163
63
5 31
531
0
Ответ: 638

15.

Примеры:
11012
1112
1011011
111102:1102= 101

16.

Пуск –Все программы – Стандартные –
Калькулятор – Вид: инженерный

17. Домашнее задание

Параграф 2.8
№ 2.25

18.

Сегодня на уроке самым
познавательным для меня
было …
Меня удивило, что …
Полученные сегодня на уроке
знания я могу применить …