Similar presentations:
Математическое и физическое моделирование. Тепловые испытания в системе комплексного моделирования
1.
Лекция 2. Математическое и физическое моделирование.Тепловые
испытания
в
системе
комплексного
моделирования. Взаимосвязь теории и эксперимента.
2.
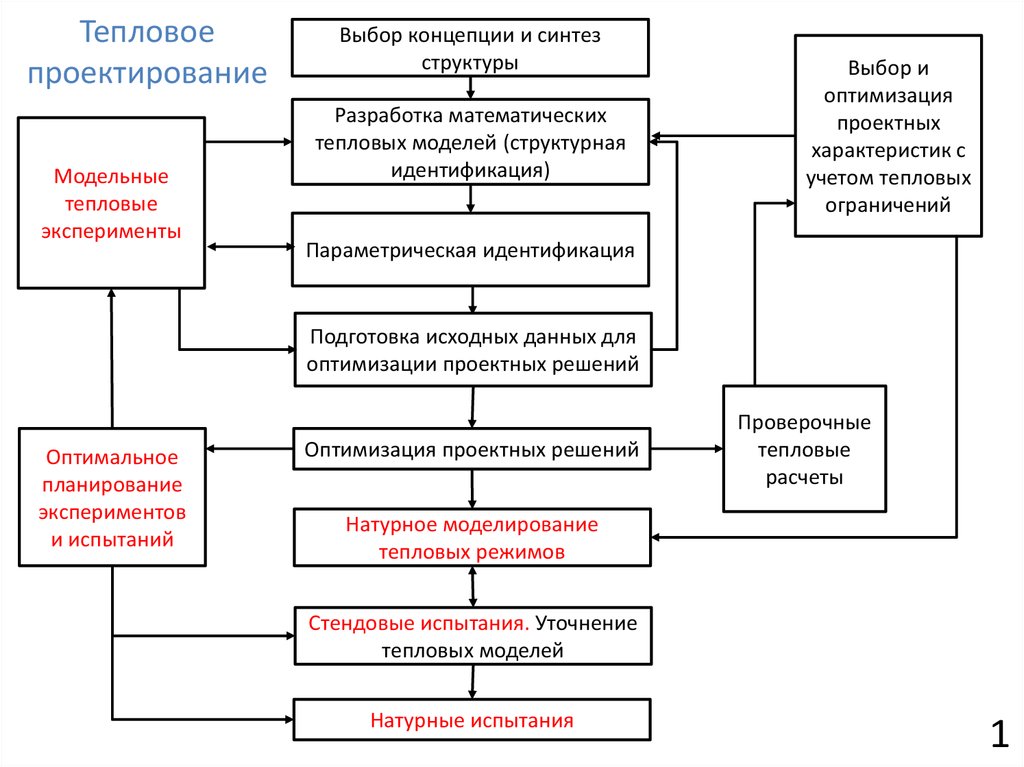
Тепловоепроектирование
Модельные
тепловые
эксперименты
Выбор концепции и синтез
структуры
Разработка математических
тепловых моделей (структурная
идентификация)
Выбор и
оптимизация
проектных
характеристик с
учетом тепловых
ограничений
Параметрическая идентификация
Подготовка исходных данных для
оптимизации проектных решений
Оптимальное
планирование
экспериментов
и испытаний
Оптимизация проектных решений
Проверочные
тепловые
расчеты
Натурное моделирование
тепловых режимов
Стендовые испытания. Уточнение
тепловых моделей
Натурные испытания
1
3.
Задачи математической физики(моделирование)
Начально-краевые
(содержат ГУ и НУ)
Краевые
(содержат только ГУ)
Задачи Коши
(содержат только НУ - ОДУ)
квазилинейное (линейность функции по всем частным производным) дифференциальное
уравнение в частных производных второго порядка с двумя независимыми переменными:
1. 0 эллиптическое
2
2
2
a ( x, y ) 2 2b( x, y )
c( x, y ) 2 F ( x, y , ,
,
)
b 2 ac 2. 0 параболическое
x
x y
y
x y
3. 0 гиперболическое
1. стационарные процессы
2. нестационарные процессы
3. колебания
2
4.
Задачи математической физики(моделирование)
Прямые (определение температур,
давлений, скоростей)
Обратные (оптимальное
управление нагревом тела,
оптимизация ТЗП)
Обобщенная постановка обратных задач
1. Разработка концепции системы (например, тепловой защиты).
2. Выбор математических моделей теплопереноса.
3. Разработка и создание физических моделей элементов системы.
4. Проведение модельных экспериментов.
5. Параметрическая идентификация модели.
6. Оценка внешнего теплового воздействия на объект.
7. Выбор оптимальных проектных параметров.
8. Создание опытных образцов исследуемых объектов.
9. Проведение полномасштабных испытаний.
10. Уточнение характеристик математической модели.
11. Итерационный процесс.
3
5.
Параметрическая идентификацияu – искомая величина (константа/вектор/функция), элемент пространства U;
y – переменная состояния процесса, принадлежит пространству Y, зависит от x;
f – известная величина (входные данные).
Для задач, описываемых уравнениями с частными производными:
- эллиптического типа y=y(x, u)../.. - параболического или гиперболического y=y(x, t, u)
Gu=y;
f=By.
Тогда постановка обратной задачи:
f=BGu=A(w)u,
где w, u – совокупности величин из некоторых теплофизических характеристик, ГУ и т.д.
f составлен из дискретных по времени измерений.
Исследуемый
процесс
Идентифицируемая
модель
Алгоритмы
решения
задач
u
A(w)u
Данные
измерений
Обработка
экспериментальной
информации
f
Сравнение f и
A(w)u
Соответ
ствие?
Нет
Да
Идентифицируемая
модель
4
6.
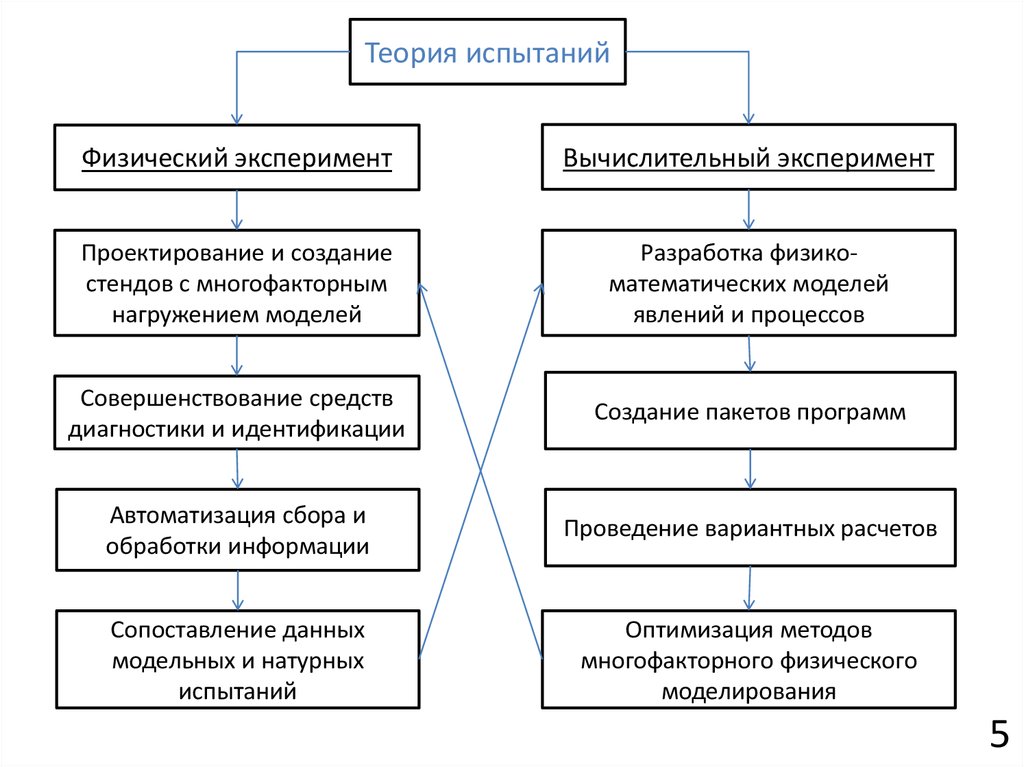
Теория испытанийФизический эксперимент
Вычислительный эксперимент
Проектирование и создание
стендов с многофакторным
нагружением моделей
Разработка физикоматематических моделей
явлений и процессов
Совершенствование средств
диагностики и идентификации
Создание пакетов программ
Автоматизация сбора и
обработки информации
Проведение вариантных расчетов
Сопоставление данных
модельных и натурных
испытаний
Оптимизация методов
многофакторного физического
моделирования
5
7.
Этапы проведения испытания1. Планирование
испытания
2. Проведение
испытания
3. Анализ
полученных данных
1.1 Подобие и
моделирование
1.2. Математическое
планирование
эксперимента
3.1. Статистическая
обработка данных
эксперимента
6





 physics
physics








