An efficient probabilistic context-free. Parsing algorithm that computes prefix probabilities

1. Probabilistic Earley Parsing

Charlie Kehoe, Spring 2004
Based on the 1995 paper by Andreas Stolcke:
An Efficient Probabilistic Context-Free
Parsing Algorithm that Computes Prefix
Probabilities

2. Overview

What is this paper all about?
Key ideas from the title:
Context-Free Parsing
Probabilistic
Computes Prefix Probabilities
Efficient

3. Context-Free Parsing

The ball is heavy.
Parser
The
ball
is
heavy

4. Context-Free Parsing

The ball is heavy.
Grammar
Parser
The
ball
is
heavy

5. Context-Free Parsing

The ball is heavy.
Grammar
Parser
The
ball
is
Lexicon
heavy

6. Context-Free Parsing

What if there are multiple legal parses?
Example: “Yair looked over the paper.”
How does the word “over” function?
S
NP
S
NP
VP
VP
or
PP
N
V
NP
N
V
P
Yair
looked over the paper
Yair
looked over the
NP
paper

7. Probabilistic Parsing

Use probabilities to find the most likely parse
Store typical probabilities for words and rules
In this case:
S
NP
S
NP
VP
VP
or
PP
N
V
NP
N
V
P
Yair
looked over the paper
P = 0.99
Yair
looked over the
P = 0.01
NP
paper

8. Prefix Probabilities

How likely is a partial parse?
S
NP
S
NP
VP
VP
or
PP
N
V
NP
N
V
P
Yair
looked over …
Yair
looked over …
NP

9. Efficiency

The Earley algorithm (upon which Stolcke
builds) is one of the most efficient known
parsing algorithms
Probabilities allow intelligent pruning of the
developing parse tree(s)

10. Parsing Algorithms

How do we construct a parse tree?
Work from grammar to sentence (top-down)
Work from sentence to grammar (bottom-up)
Work from both ends at once (Earley)
Predictably, Earley works best

11. Earley Parsing Overview

Start with a root constituent, e.g. sentence
Until the sentence is complete, repeatedly
Predict: expand constituents as specified in the
grammar
Scan: match constituents with words in the input
Complete: propagate constituent completions up
to their parents
Prediction is top-down, while scanning and
completion are bottom-up

12. Earley Parsing Overview

Earley parsing uses a chart rather than a tree
to develop the parse
Constituents are stored independently,
indexed by word positions in the sentence
Why do this?
Eliminate recalculation when tree branches are
abandoned and later rebuilt
Concisely represent multiple parses

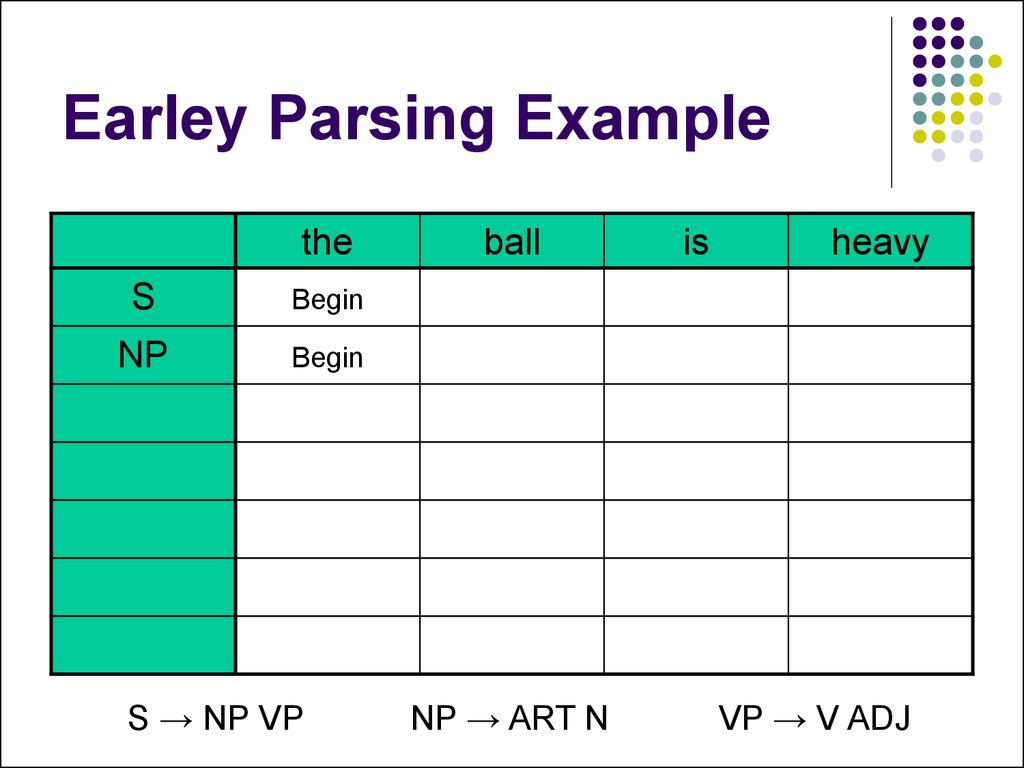
13. Earley Parsing Example

the
S
ball
is
heavy
Begin
S → NP VP
NP → ART N
VP → V ADJ

14. Earley Parsing Example

the
S
Begin
NP
Begin
S → NP VP
ball
NP → ART N
is
heavy
VP → V ADJ

15. Earley Parsing Example

the
S
Begin
NP
Pending
ART
Scan
S → NP VP
ball
NP → ART N
is
heavy
VP → V ADJ

16. Earley Parsing Example

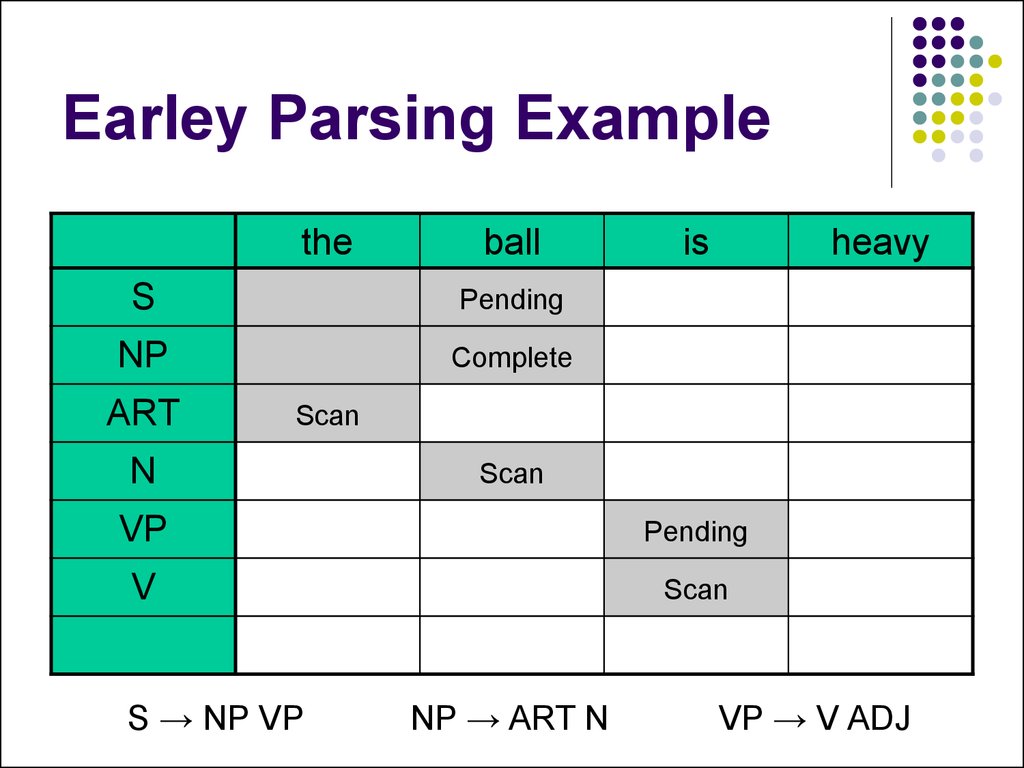
the
S
is
heavy
Begin
NP
ART
ball
Complete
Scan
N
S → NP VP
Scan
NP → ART N
VP → V ADJ

17. Earley Parsing Example

the
ball
S
Pending
NP
Complete
ART
is
heavy
Scan
N
S → NP VP
Scan
NP → ART N
VP → V ADJ

18. Earley Parsing Example

the
ball
S
Pending
NP
Complete
ART
is
heavy
Scan
N
Scan
VP
S → NP VP
Begin
NP → ART N
VP → V ADJ

19. Earley Parsing Example

the
ball
S
Pending
NP
Complete
ART
is
heavy
Scan
N
Scan
VP
Pending
V
Scan
S → NP VP
NP → ART N
VP → V ADJ

20. Earley Parsing Example

the
ball
S
Pending
NP
Complete
ART
is
heavy
Scan
N
Scan
VP
Complete
V
Scan
ADJ
S → NP VP
Scan
NP → ART N
VP → V ADJ

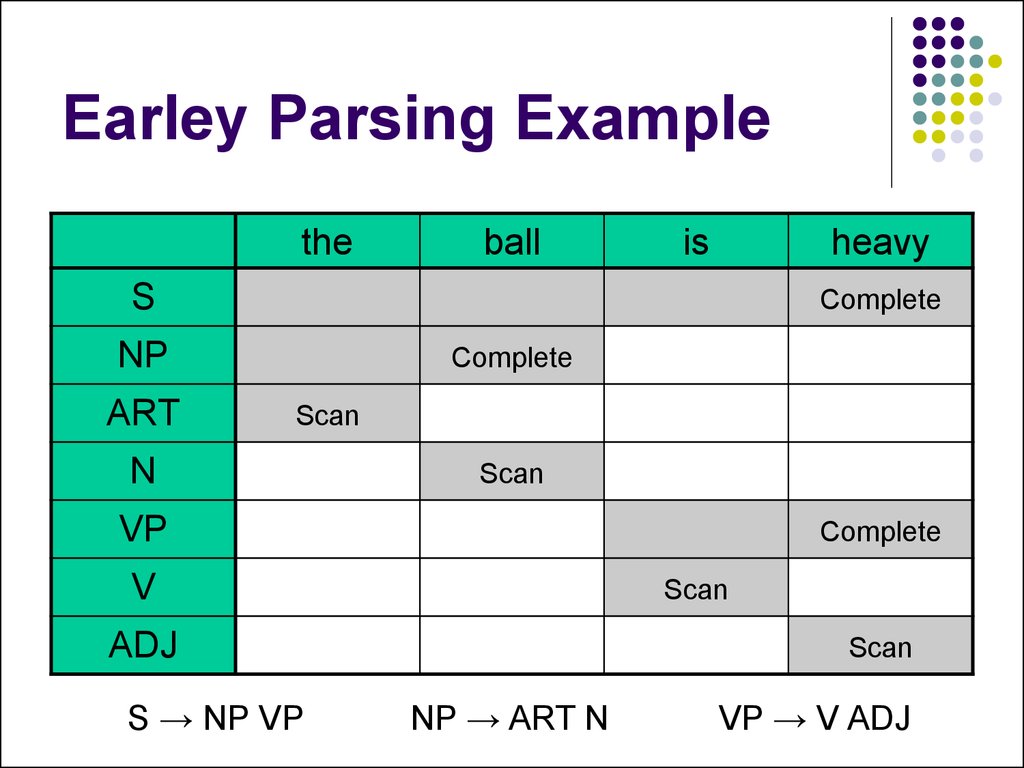
21. Earley Parsing Example

the
ball
is
heavy
S
Complete
NP
ART
Complete
Scan
N
Scan
VP
Complete
V
Scan
ADJ
S → NP VP
Scan
NP → ART N
VP → V ADJ

22. Probabilistic Parsing

How do we parse probabilistically?
Assign probabilities to grammar rules and
words in lexicon
Grammar and lexicon “randomly” generate all
possible sentences in the language
P(parse tree) = P(sentence generation)

23. Probabilistic Parsing

Terminology
Earley state: each step of the processing that a
constituent undergoes. Examples:
Starting sentence
Half-finished sentence
Complete sentence
Half-finished noun phrase
etc.
Earley path: a sequence of linked states
Example: the complete parse just described

24. Probabilistic Parsing

Can represent the parse as a Markov chain:
NP
ART N
Begin
S
Begin
Predict S
S
NP VP
Begin
NP
Done
NP Half
Done
Scan “the”
Scan “ball”
S Half
Done
Complete NP
Predict NP
NP
PN
Begin
etc.
(path abandoned)
Markov assumption (state probability is
independent of path) applies, due to CFG

25. Probabilistic Parsing

Every Earley path corresponds to a parse tree
P(tree) = P(path)
Assign a probability to each state transition
Prediction: probability of grammar rule
Scanning: probability of word in lexicon
Completion: accumulated (“inner”) probability of
the finished constituent
P(path) = product of P(transition)s

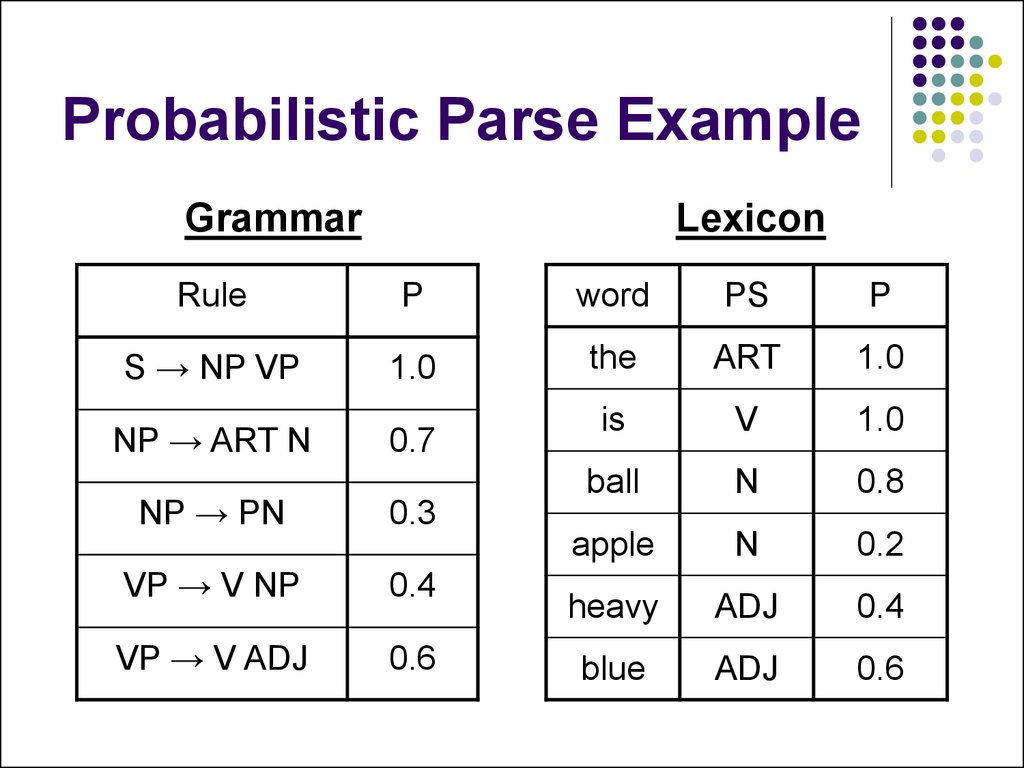
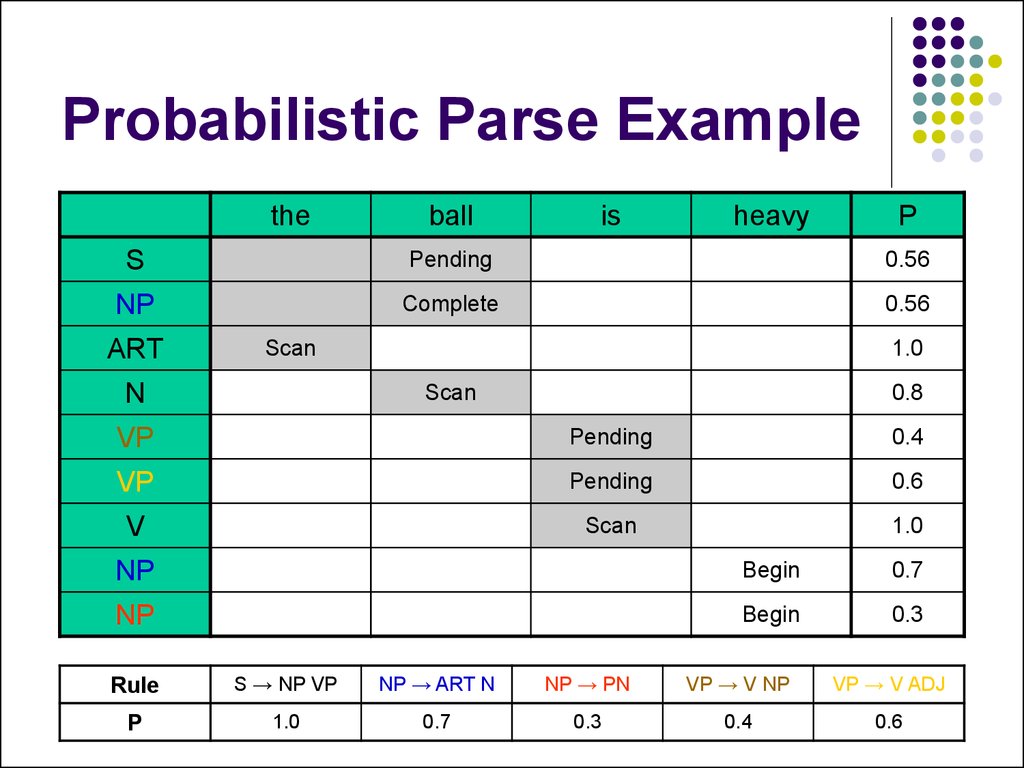
26. Probabilistic Parse Example

Grammar
Lexicon
Rule
P
word
PS
P
S → NP VP
1.0
the
ART
1.0
is
V
1.0
ball
N
0.8
apple
N
0.2
heavy
ADJ
0.4
blue
ADJ
0.6
NP → ART N
0.7
NP → PN
0.3
VP → V NP
0.4
VP → V ADJ
0.6

27. Probabilistic Parse Example

the
ball
is
heavy
P
S
Begin
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6
1.0

28. Probabilistic Parse Example

the
ball
is
heavy
P
S
Begin
1.0
NP
Begin
0.7
NP
Begin
0.3
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

29. Probabilistic Parse Example

the
ball
is
heavy
P
S
Begin
1.0
NP
Pending
0.7
NP
Failed
0.3
ART
Scan
1.0
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

30. Probabilistic Parse Example

the
S
is
heavy
Begin
NP
ART
ball
1.0
Complete
0.56
Scan
N
P
1.0
Scan
0.8
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

31. Probabilistic Parse Example

the
ball
is
heavy
P
S
Pending
0.56
NP
Complete
0.56
ART
Scan
N
1.0
Scan
0.8
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

32. Probabilistic Parse Example

the
ball
is
heavy
P
S
Pending
0.56
NP
Complete
0.56
ART
Scan
N
1.0
Scan
0.8
VP
Begin
0.4
VP
Begin
0.6
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

33. Probabilistic Parse Example

the
ball
is
heavy
P
S
Pending
0.56
NP
Complete
0.56
ART
Scan
N
1.0
Scan
0.8
VP
Pending
0.4
VP
Pending
0.6
V
Scan
1.0
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

34. Probabilistic Parse Example

the
ball
is
heavy
P
S
Pending
0.56
NP
Complete
0.56
ART
Scan
N
1.0
Scan
0.8
VP
Pending
0.4
VP
Pending
0.6
V
Scan
1.0
NP
Begin
0.7
NP
Begin
0.3
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

35. Probabilistic Parse Example

the
ball
is
heavy
P
S
Pending
0.56
NP
Complete
0.56
ART
Scan
N
1.0
Scan
0.8
VP
Pending
0.4
VP
Pending
0.6
V
Scan
1.0
NP
Failed
0.7
NP
Failed
0.3
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

36. Probabilistic Parse Example

the
ball
is
heavy
P
S
Pending
0.56
NP
Complete
0.56
ART
Scan
N
1.0
Scan
VP
0.8
Failed
VP
0.4
Complete
V
Scan
ADJ
0.24
1.0
Scan
0.4
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

37. Probabilistic Parse Example

the
ball
is
S
NP
ART
heavy
P
Complete
0.1344
Complete
0.56
Scan
N
1.0
Scan
0.8
VP
Complete
V
Scan
ADJ
0.24
1.0
Scan
0.4
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

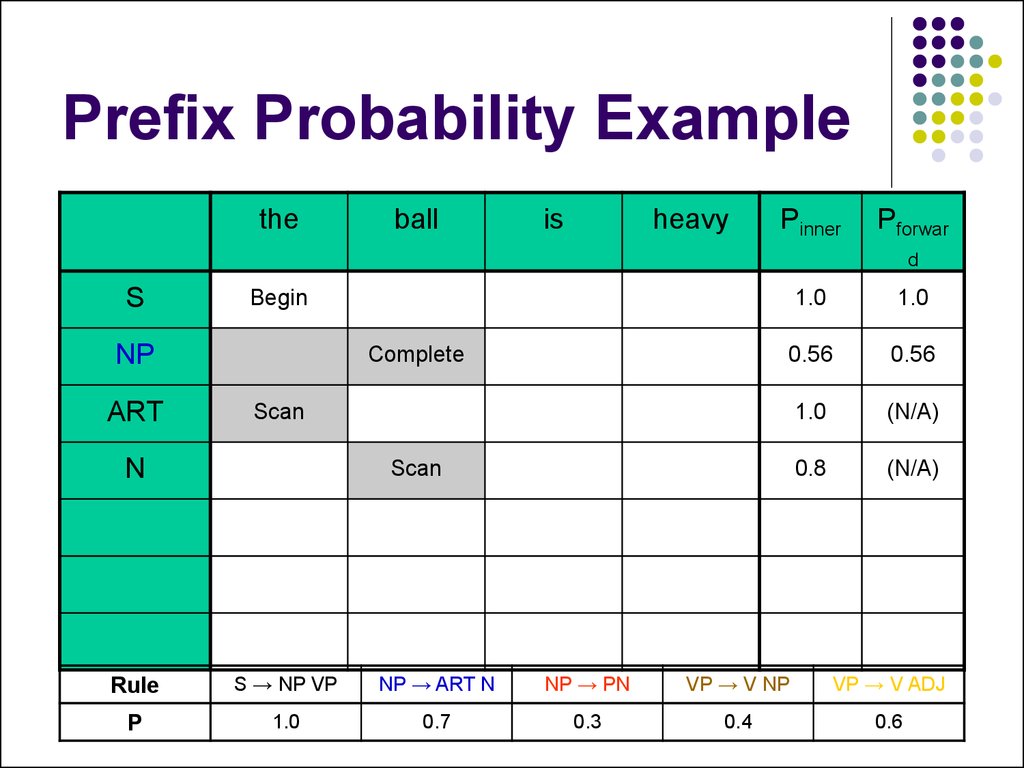
38. Prefix Probabilities

Current algorithm reports parse tree
probability when the sentence is completed
What if we don’t have a full sentence?
Probability is tracked by constituent (“inner”),
rather than by path (“forward”)

39. Prefix Probabilities

Solution: add a separate path probability
Same as before, but propagate down on
prediction step
This is the missing link to chain the path
probabilities together

40. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Begin
1.0
1.0
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

41. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Begin
1.0
1.0
NP
Begin
0.7
0.7
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

42. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Begin
1.0
1.0
NP
Pending
0.7
0.7
ART
Scan
1.0
(N/A)
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

43. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Begin
NP
ART
Complete
1.0
1.0
0.56
0.56
1.0
(N/A)
0.8
(N/A)
Scan
N
Scan
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

44. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Pending
0.56
0.56
NP
Complete
0.56
0.56
1.0
(N/A)
0.8
(N/A)
ART
Scan
N
Scan
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

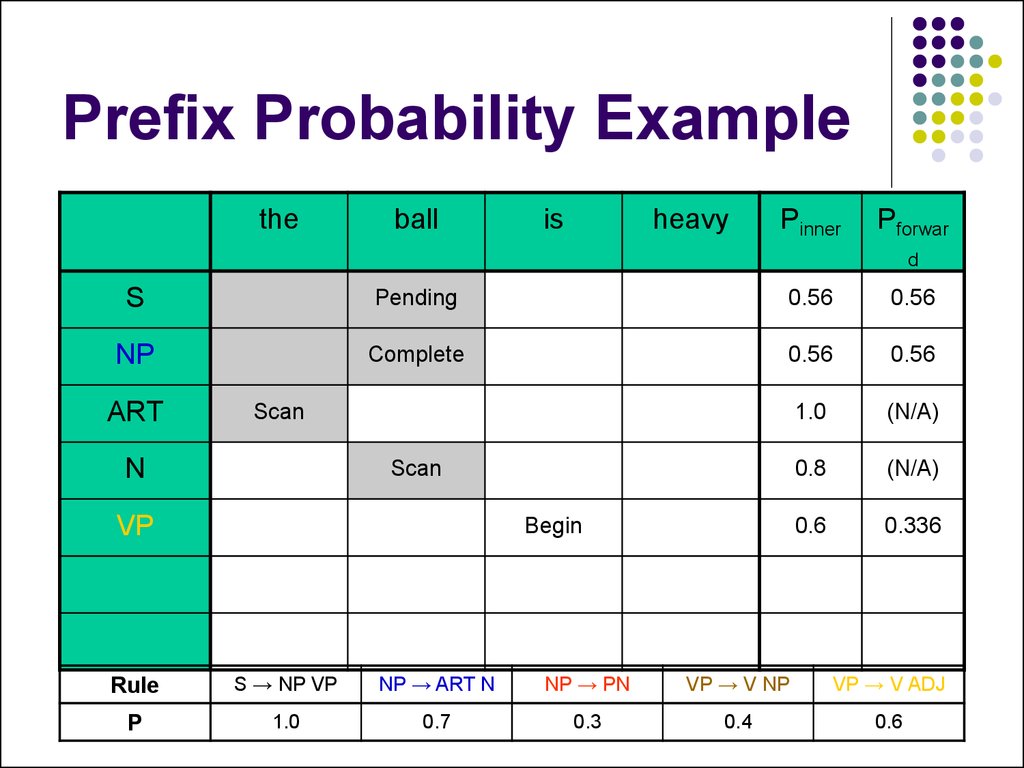
45. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Pending
0.56
0.56
NP
Complete
0.56
0.56
1.0
(N/A)
0.8
(N/A)
0.6
0.336
ART
Scan
N
Scan
VP
Begin
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

46. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Pending
0.56
0.56
NP
Complete
0.56
0.56
1.0
(N/A)
0.8
(N/A)
ART
Scan
N
Scan
VP
Pending
0.6
0.336
V
Scan
1.0
(N/A)
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

47. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Pending
0.56
0.56
NP
Complete
0.56
0.56
1.0
(N/A)
0.8
(N/A)
0.24
0.1344
1.0
(N/A)
0.4
(N/A)
ART
Scan
N
Scan
VP
Complete
V
Scan
ADJ
Scan
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

48. Prefix Probability Example

the
ball
is
heavy
Pinner
Pforwar
d
S
Complete
NP
ART
Complete
0.1344
0.1344
0.56
0.56
1.0
(N/A)
0.8
(N/A)
0.24
0.1344
1.0
(N/A)
0.4
(N/A)
Scan
N
Scan
VP
Complete
V
Scan
ADJ
Scan
Rule
S → NP VP
NP → ART N
NP → PN
VP → V NP
VP → V ADJ
P
1.0
0.7
0.3
0.4
0.6

49. Summary

Use Earley chart parser for efficient parsing,
even with ambiguous or complex sentences
Use probabilities to choose among multiple
possible parse trees
Track constituent probability for complete
sentences
Also track path probability for incomplete
sentences