Similar presentations:
מהי לוגיקה
1.
מהי לוגיקה?• תורת ההיגיון
• תורת ההיסק מתארת טיעונים תקפים -טיעונים
ששומרים על אמיתות .תקפות היא תכונה מבנית
(תחבירית) של טיעונים
• תנאיי-קדם ללוגיקה :שפה בעלת תחביר
וסמנטיקה.
תחביר – מבנה של ביטוים בשפה.
סמנטיקה – פשר (משמעות) של הביטויים ,הקשר
שבין השפה לבין מה שהיא מדברת עליו.
2.
לוגיקה במדעי המחשב•
•
•
•
מחשב מחקה יכולת שכלית (היגיון)
תוכנית מחשב – סוג של הוכחה .תורת
התכנות -לוגיקה שימושית .אימות תוכנה.
תכנות לוגי.
בינה מלאכותית
3.
טיעונים• אם רכבת מאחרת וגם אין מוניות זמינות בתחנה,
אז אלי מאחר לפגישה .אבל אלי לא איחר לפגישה
למרות שרכבת איחרה .לכן היו מוניות זמינות
בתחנה.
• אם יורד גשם ולטלי אין מטריה איתה ,אז היא
מצטננת .טלי לא הצטננה למרות שהיה גשם .לכן
לטלי הייתה מטריה.
מבנה הטיעון:
אם pוגם לא ,qאז .rלא rו .p-לכן .q
(p ¬q(→r, ¬r p├ q
4.
תחשיב הפסוקיםנדון בפסוקיי חיווי ,אשר יש להם בדיוק אחד משני
ערכים :אמת ( )Trueאו שקר (.)False
.1קנדה היא מדינה.
.2משה הוא כלב
.3סגור את הדלת!
|X| = X .4
.5משפט זה הוא שקר.
מפסוקים יסודיים ניתן לבנות פסוקים מורכבים
בתוספת מילות חיבור כגון :ו ,או ,לא ,וכו':
קנדה היא מדינה ומשה הוא כלב.
5.
קשרים לוגיים•
•
•
•
•
שלילה (" : ¬P )negationלא ."P
קוניונקציה ( ,conjunctionגימום) P" P Q:ו.“Q -
דיסיונקציה ( ,disjunctionאיווי) P” : P Qאו .“Q
אימפליקציה ( ,implicationאימוז) P→Q
"אם Pאז .“Q
:
שקילות (P↔Q )equivalence
" Pאם ורק אם .“Q
:
6.
תחבירהגדרה :נוסחא נקראת בנויה היטב ( well-formed
)formulaאם ניתן ליצור אותה לפי החוקים הבאים:
.1כל פסוק אטומי p,q,...הוא נוסחא בנויה היטב.
.2קבוע הוא נוסחא בנויה היטב.
.3אם Aו B -הן נוסחאות בנויות היטב ,אז גם ((¬A
) (A B), (A B), (A B), (A Bהן נוסחאות
בנויות היטב.
.4כל נוסחא בנויה היטב ניתן ליצור במספר סופי של
צעדים ע"י שימוש בחוקים .1-3
7.
פסוקים מורכביםדוגמא)¬)¬p(( ,(p q) ,((p q) (¬p(( ,))¬p( q) :
((p q)), (p q r), ( p
ולא
משפט( .קריאה יחידה) כל נוסחה שייכת בדיוק
לאחד מהסוגים הבאים:
.1פסוק אטומי.
(¬A( .2עבור נוסחה אחת ויחידה .A
(A ○ B) .3עבור קשר בינארי ○ אחד ויחיד
ונוסחאות יחידות Aו( .B-בלי הוכחה)
8.
אינדוקציה על נוסחאותאם תכונה Pנכונה לכל הפסוקים האטומיים ,ומהנחה
ש P-נכונה לנוסחאות Aו B-נובע ש P-נכונה ל-
( ,(A B), (A B), (A B), (A B), (¬Aאזי P
נכונה לכל נוסחא בנויה היטב.
הסכם :אפשר להשמיט סוגריים חיצוניות וסוגריים
עבור ¬ .לדוגמא נרשום ¬P Qבמקום )((¬P( Q
9.
הצרנה•
•
•
•
זהו מקס או שההוא מוריץ ואני ליצןp q r :
אני אגיע הביתה ואביא תותים אם לא ירד גשם.
אם לא יובל ולא איל יעברו את הבחינה ,גם חגי לא
יעבור.
לא כולם (מהשלושה) יכשלו.
10.
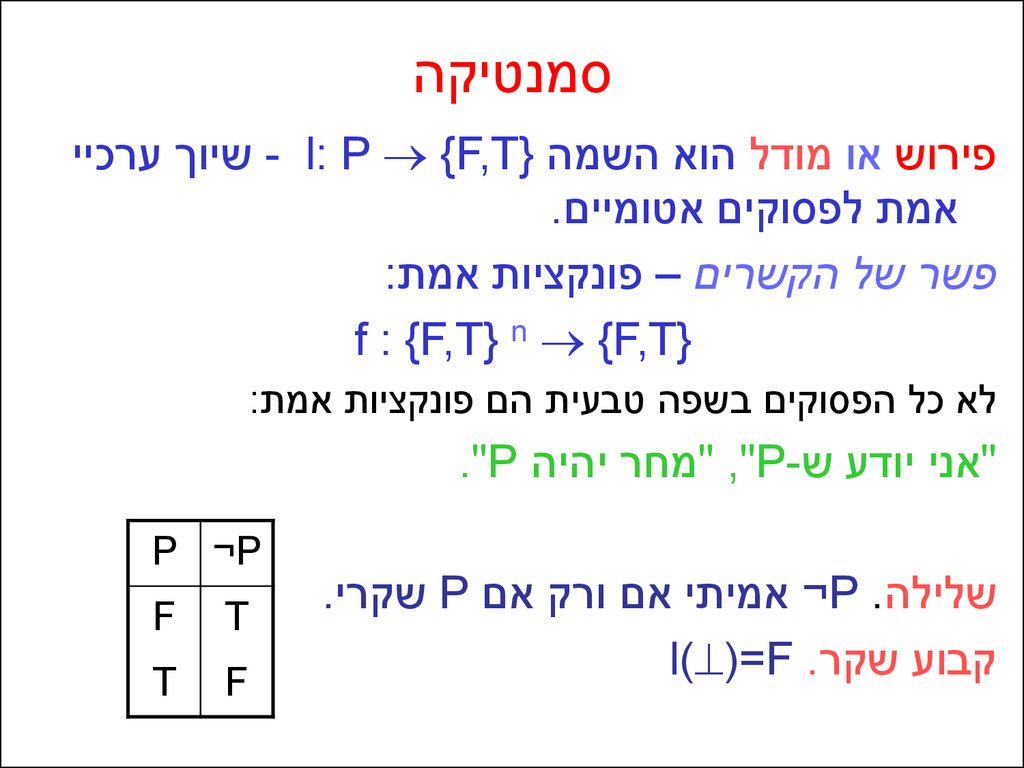
סמנטיקהפירוש או מודל הוא השמה } - l: P {F,Tשיוך ערכיי
אמת לפסוקים אטומיים.
פשר של הקשרים – פונקציות אמת:
}f : {F,T} n {F,T
לא כל הפסוקים בשפה טבעית הם פונקציות אמת:
"אני יודע ש" ,"P-מחר יהיה ."P
שלילה ¬P .אמיתי אם ורק אם Pשקרי.
קבוע שקרl( )=F .
P ¬P
T
F
F
T
11.
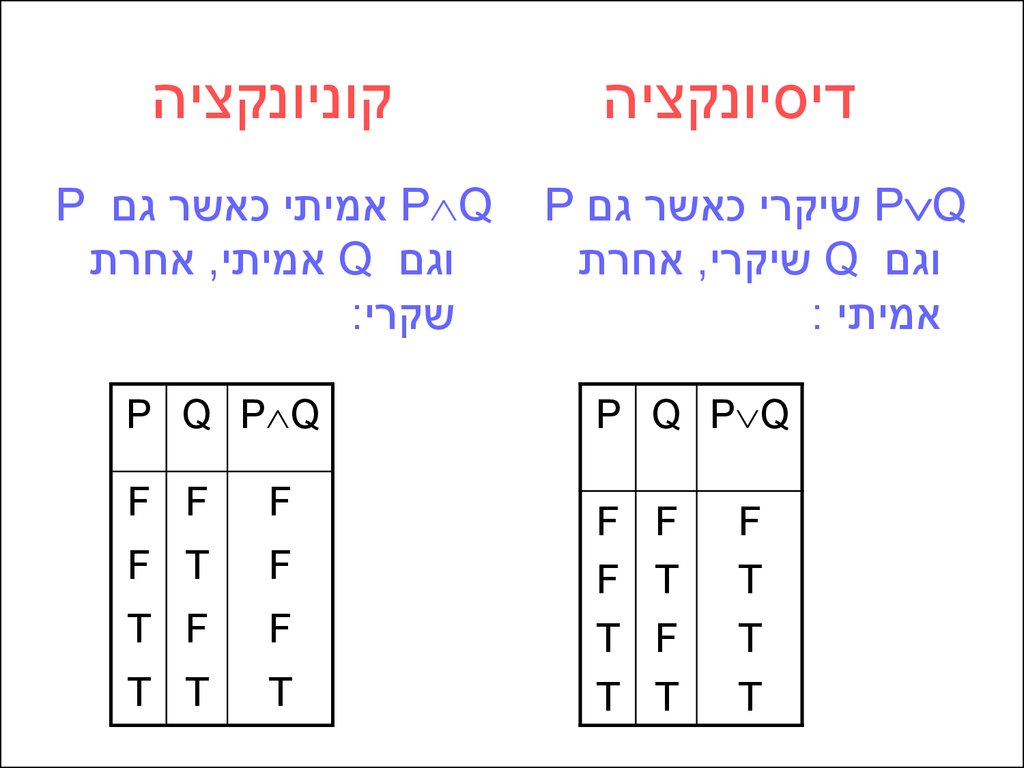
דיסיונקציה P Qשיקרי כאשר גם P
וגם Qשיקרי ,אחרת
אמיתי :
קוניונקציה
P Qאמיתי כאשר גם P
וגם Qאמיתי ,אחרת
שקרי:
P Q P Q
P Q P Q
F
F
T
T
F
F F
F
F T
F
T F
T
T T
F
T
T
T
F
T
F
T
12.
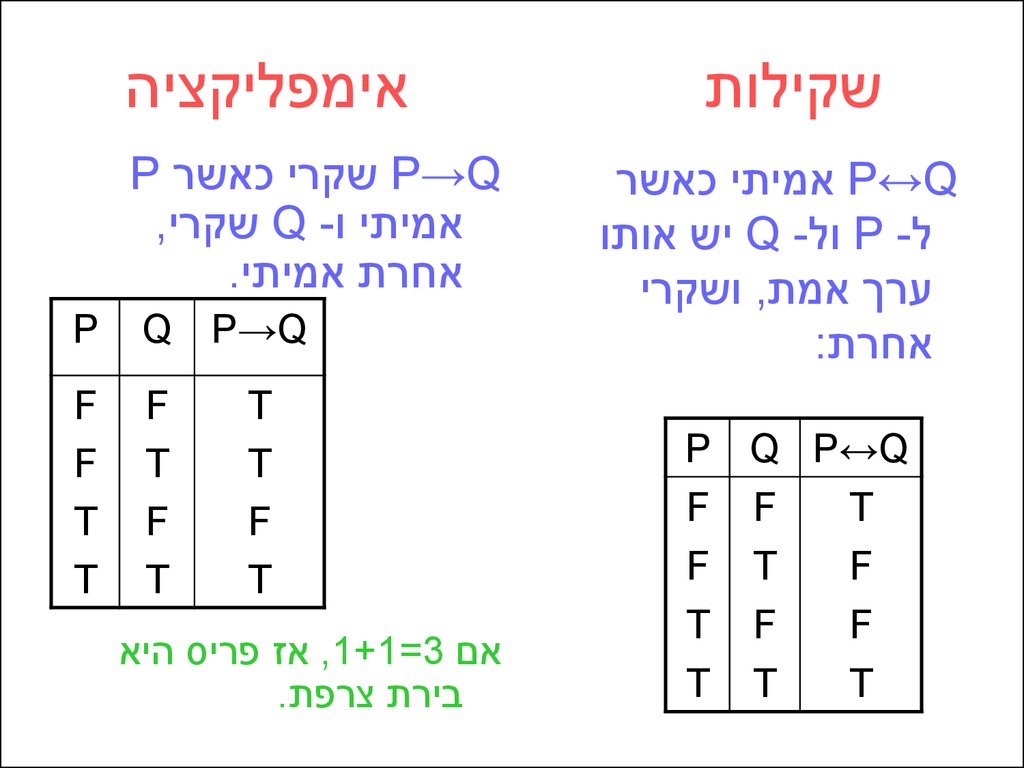
שקילות P↔Qאמיתי כאשר
ל P -ול Q -יש אותו
ערך אמת ,ושקרי
אחרת:
P Q P↔Q
F F
T
F T
F
T F
F
T T
T
אימפליקציה
P→Qשקרי כאשר P
אמיתי ו Q -שקרי,
אחרת אמיתי.
Q P→Q
P
F
T
F
T
F
F
T
T
T
T
F
T
אם ,1+1=3אז פריס היא
בירת צרפת.
13.
יחס ספיקותהגדרה( .הרחבה של פירוש לפסוקים מורכבים)
• l( )=F
• l(¬A(=Tאם ורק אם l(A)=F
• l(A B)=Tאם ורק אם l(A)=l(B)=T
• l(A B)=Tאם ורק אם l(A)=Tאו l(B)=T
• l(A B)=Tאם ורק אם l(A)=Fאו l(B)=T
• l(A↔B)=Tאם ורק אם )l(A)=l(B
פירוש lמספק ,Aאו lהוא מודל של ,Aאם l(A)=T
עובדה .ערך האמת של פסוק מורכב היא פונקציה של ערכי האמת של
הפסוקים אטומיים שלו (קריאה יחידה!).
14.
בעיות ספיקות ותקפות• נוסחה נקראת ספיקה (או עקבית) אם יש לה
מודל .נוסחה לא ספיקה נקראת סתירה.
בעיית ספיקות ( :)SAT problemהאם (ומתיי)
הנוסחה ספיקה? SATהיא בעיית .NP
• נוסחה Aנקראת תקפה ,או טאוטולוגיה ,אם כל
פירוש הוא מודל של .A
בעיית תקפות :האם נוסחה Aתקפה?
Aהיא טאוטולוגיה אם ורק אם ¬Aהיא לא ספיקה.
15.
טבלאות אמתטבלת אמת של פסוק מורכב
מתארת את ערכי האמת של
הפסוק עבור כל פרוש.
אם הפסוק מורכב מm -
פסוקים אטומיים ,אזי יש ,2m
צרופים ובטבלת האמת שלו
תהיינה 2mשורות.
p q ¬ p q
F F T F T F
F T T F T T
T F F T F F
T T F T T T
2 1 3 1
16.
טאוטולוגיות וסתירותנוסחה המקבלת ערך אמת Tלכל הצבה עבור המשתנים שלה
היא טאוטולוגיה.
נוסחה המקבלת ערך Fלכל הצבה כזאת היא סתירה.
p p
p ¬p
¬p
p
T
F
T
F
T
F
F
T
ניתן להוכיח טאוטולוגיות וסתירות בשיטת השלילה.
דוגמא:
)(A B) →(¬A B
17.
שקילות של פסוקיםשני פסוקים נקראים שקולים אם יש להם אותם
מודלים .פסוקים שקולים מהבאים אותה טענה.
נסמן את השקילות ב . -בדוגמא.A A A :
משפט :נוסחאות Aו B -שקולות אם ורק אם A B
היא טאוטולוגיה.
הוכחה נובעת מן ההגדרות [נמק].
18.
טבלת אמת ל¬)p q) (¬p ¬q( -)q
¬
p
¬( q)
(p
¬
q
p
F
T
F
T
1
T
F
T
F
2
T
T
T
F
3
F
F
T
T
1
F
T
F
T
1
F
F
F
T
2
F
F
T
T
1
T
T
T
F
3
F
T
F
T
F
F
T
T
T
T
F
F
2
T
T
T
T
4
תוך שימוש בשקילויות יסודיות ניתן להוכיח שקילויות
חדשות בלי להשתמש בטבלאות אמת.
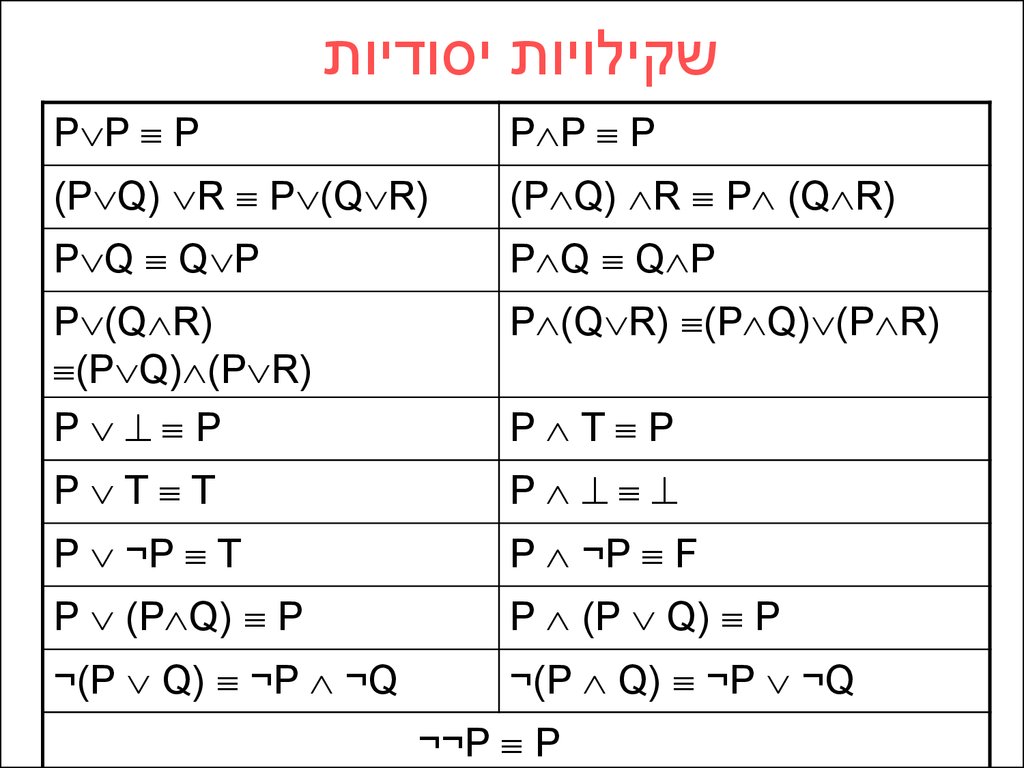
19.
שקילויות יסודיותP P P
P P P
(P Q) R P (Q R)
(P Q) R P (Q R)
P Q Q P
P Q Q P
P (Q R)
(P Q) (P R)
P P
P (Q R) (P Q) (P R)
P T T
P
P ¬P T
P ¬P F
P (P Q) P
P (P Q) P
¬(P Q) ¬P ¬Q
¬(P Q) ¬P ¬Q
P T P
¬¬P P
20.
שלמות פונקציונאליתp
q
r
A
T
T
T
F
T
T
F
T
T
F
T
F
T
F
F
F
F
T
T
T
F
T
F
F
F
F
T
F
F
F
F
F
מגדירהA(p1,…,pn) כל נוסחה
,l לכל:מקומית-n פונקצית אמת
g(l(p1),…,l(pn))=l(A)
.דוגמה
(p q ¬r( (¬p q r)
21.
משפת (שלמות פונקציונאלית) .לכל פונקצית אמתקיימת נוסחה המגדירה אותה.
הוכחה .תהיה fפונקצית אמת -nמקומית .נגדיר
}Hf={(a1,a2,…,an) {F,T}n :f(a1,…,an)=T
לכל ) x=(a1,a2,…,anנשייך נוסחה
ř1 ř2… řn = Ax
כך ש ři :הוא riאם ,T=aiאחרת řiהוא .¬riאז
פירוש lמספק את Axאם"ם )).]?[ x=(l(r1),...,l(rn
נגדיר Af= Ax1 Ax2 … Axkעבור כל xiמ.Hf -
אז ,לכל פירוש l(Af)=T ,lאם"ם קיים x Hfכך ש
)) ,]?[ x=(l(r1),...,l(rnז"א ).f(l(r1),…,l(rn))=l(Af
22.
קבוצות שלמות של קשריםהגדרה :קבוצה של קשרים שבאמצעותם ניתן לתאר
כל פונקצית אמת נקראת קבוצה שלמה.
)P Q (P Q) (Q P
P Q ¬P Q
P Q ¬P Q
(P Q ¬)¬P ¬Q
(P Q ¬)¬P ¬Q
מסקנה {¬, }, {¬, }, {¬, } .הן קבוצות שלמות
של קשרים[ .נמק]
23.
קבוצות לא שלמות של קשריםלמה { , , , } .היא קבוצה לא שלמה של
קשרים.
הוכחה .להבדיל מ ,¬p-כל נוסחה הבנויה מ-
} { , , , היא אמיתית כאשר כל הפסוקים
האטומיים שלה אמיתיים[ .באינדוקציה על מספר
הקשרים בנוסחה].
למה { ,¬} .היא קבוצה לא שלמה של קשרים.
[להוכיח]
24.
קבוצות קשרים שלמותP
F
F
T
T
Q
F
T
F
T
P Q
T
T
T
F
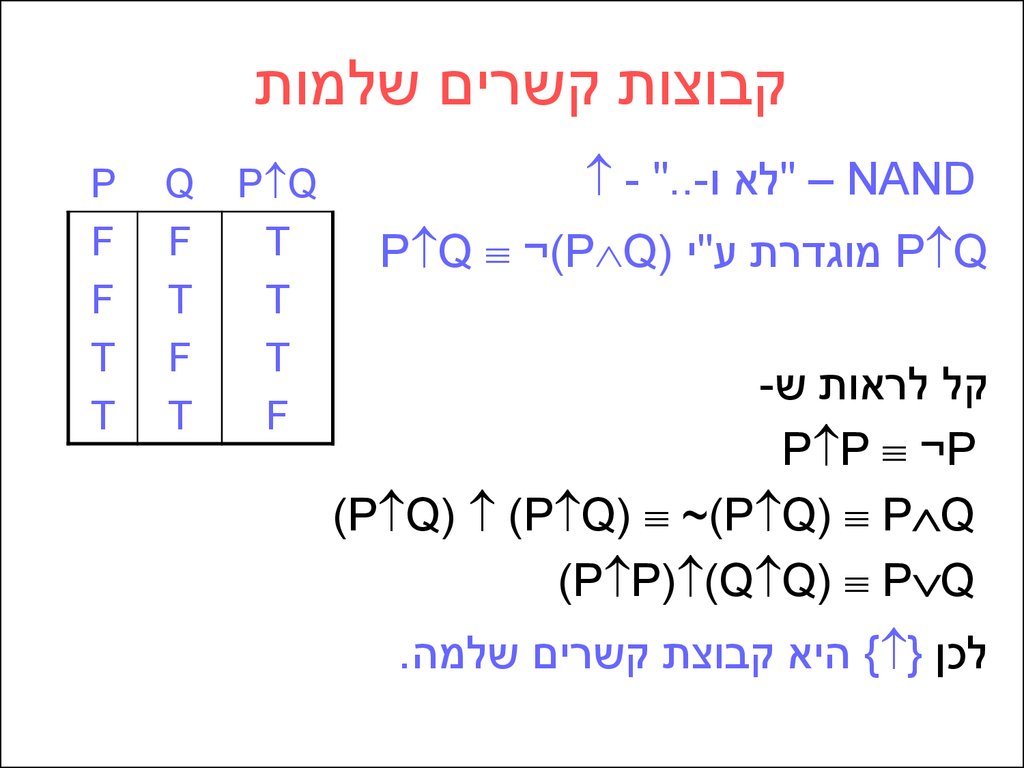
- "..- – "לא וNAND
P Q ¬)P Q) מוגדרת ע"יP Q
-קל לראות ש
P P ¬P
(P Q) (P Q) ~(P Q) P Q
(P P) (Q Q) P Q
.{ היא קבוצת קשרים שלמה } לכן
25.
קבוצות קשרים שלמותP
F
F
T
T
Q
F
T
F
T
P Q
T
F
F
F
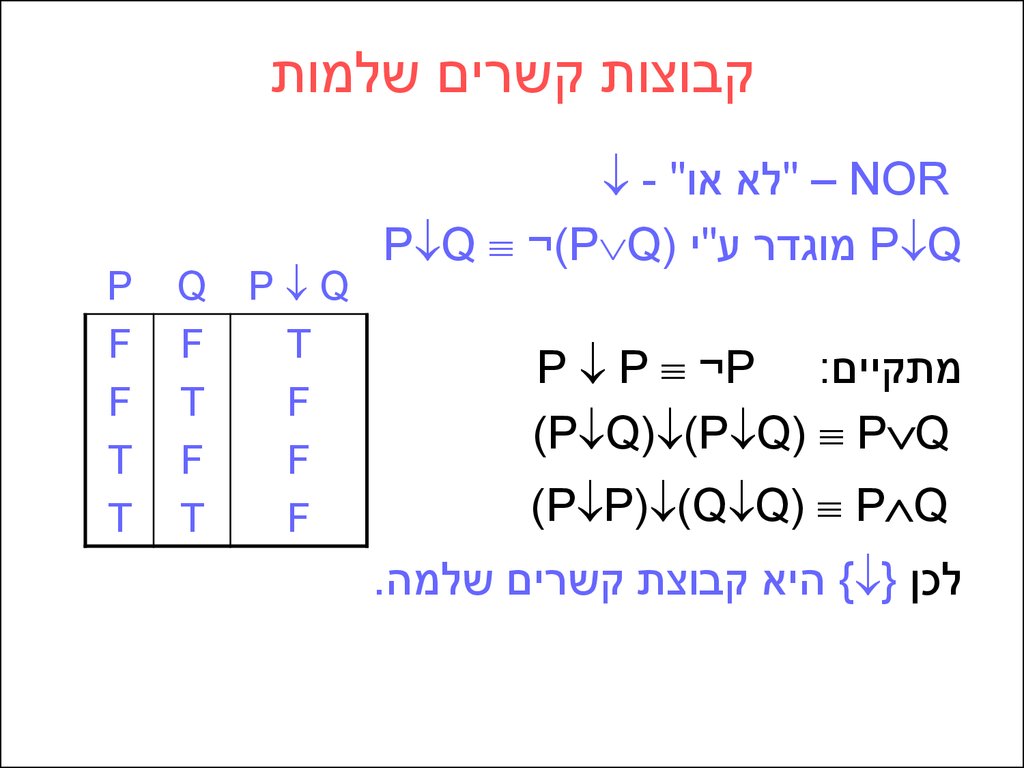
- " – "לא אוNOR
P Q ¬)P Q) מוגדר ע"יP Q
P P ¬P :מתקיים
(P Q) (P Q) P Q
(P P) (Q Q) P Q
.{ היא קבוצת קשרים שלמה } לכן
26.
)gates( שעריםa
a
b
¬a
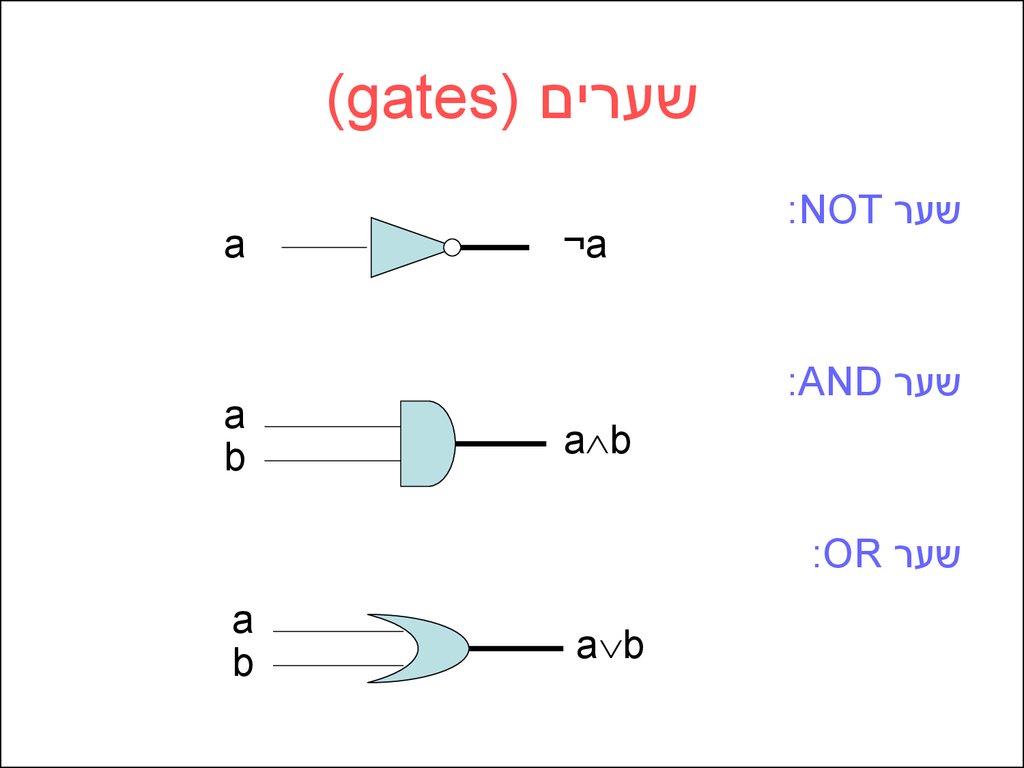
:NOT שער
:AND שער
a b
:OR שער
a
b
a b
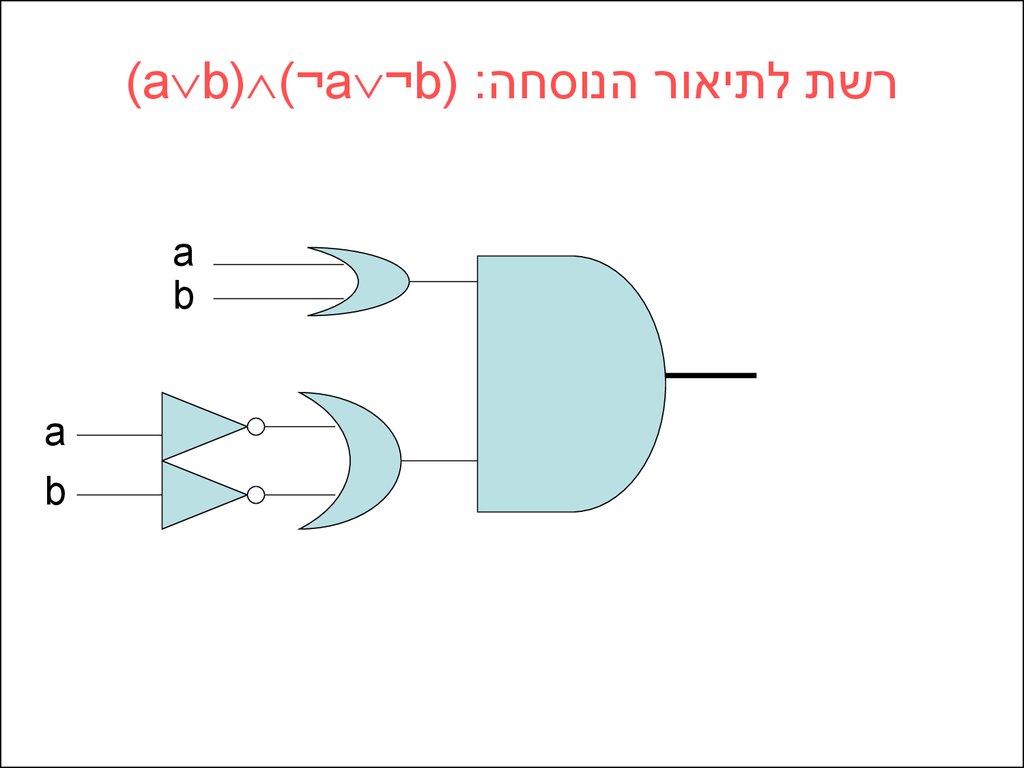
27.
רשת לתיאור הנוסחה(a b) (¬a ¬b( :a
b
a
b
28.
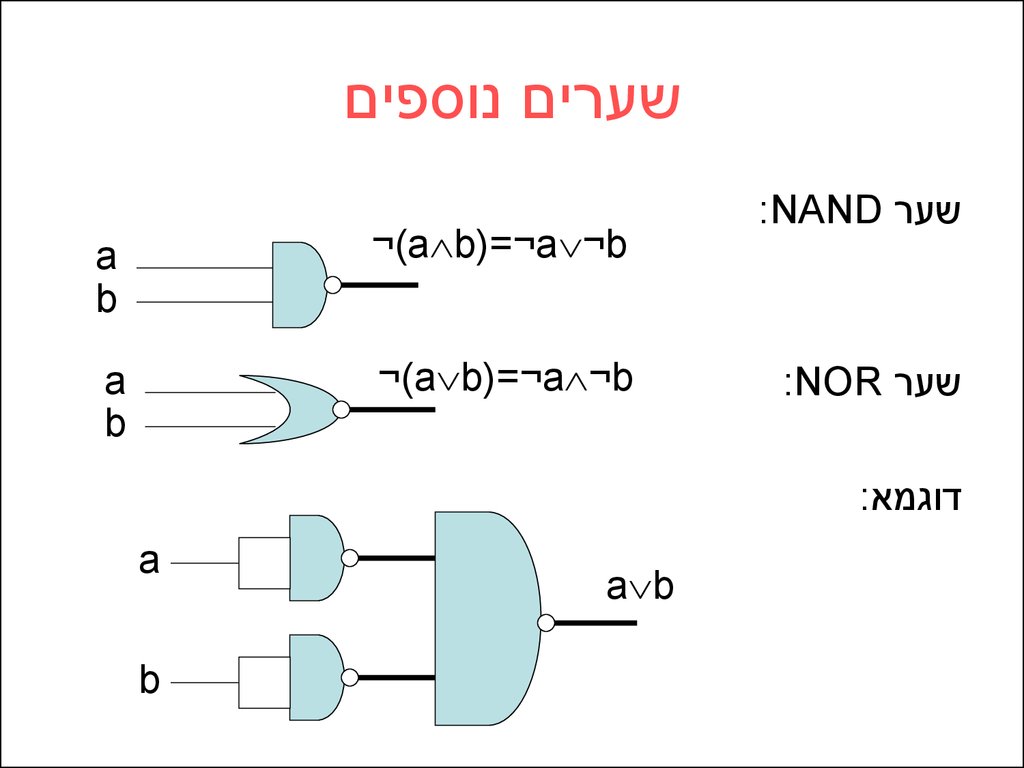
שערים נוספיםa
b
¬)a b)=¬a ¬b
a
b
¬)a b)=¬a ¬b
:NAND שער
:NOR שער
:דוגמא
a
b
a b
29.
צורות נורמאליותאם pהוא פסוק אטומי ,אז pו ¬p-הם ליטרלים.
הגדרה .נוסחה בצורה דיסיונקטיבית נורמאלית )(DNF
היא דיסיונקציה של קוניונקציות של ליטרלים.
דוגמא(p ¬q r) (r p) (r ¬q ¬p( :
מסקנה .1כל נוסחה שקולה לנוסחה בצורת .DNF
הוכחה .אם fהיא פונקצית אמת המוגדרת ע"י נוסחה B
,אז הנוסחה Afשבנינו בהוכחת משפת שלמות
פונקציונאלי שקולה ל , B-והיא בצורת .DNF
30.
דואליותהגדרה :תהי Aנוסחה שמכילה , , , ,Tו ¬ -בלבד.
נוסחה דואלית ל A -מתקבלת ממנה בהחלפת כל ב -
וכל ב , -כל Tב -וכל בT-
נוסחה
נוסחה דואלית
(P Q) R
(P Q) R
((¬)P Q) (P (¬Q ¬S(( ¬)P Q) (P (¬Q ¬S
למת עזר .השלילה של נוסחה שקולה לנוסחה דואלית שבה
כל משתנה מוחלף בשלילה שלו[ .למה?]
דוגמא¬))P Q) R) ¬(P Q) ¬R (¬P ¬Q( ¬R :
31.
צורות נורמליות -המשךפסוקית ( )clauseהיא דיסיונקציה של ליטרלים:
r ¬q ¬p
הגדרה .נוסחה בצורה קוניונקטיבית נורמאלית
) (CNFהיא קוניונקציה של פסוקיות.
דוגמא(p ¬q r) (r p) (r ¬q ¬p( :
מסקנה .2כל נוסחה שקולה לנוסחה בצורת .CNF
הוכחה .נניח ש f -היא פונקצית אמת המוגדרת ע"י
נוסחה , ¬Bו Af -היא הנוסחה המקבילה ב-
.DNFאז ¬Afשקולה ל ,B-וניתן להפוך ¬Af
לנוסחה דואלית בצורת .]?[CNF
32.
CNFp q
¬p ¬q
A
F
T
T
F
q
F
T
F
T
p
F
F
T
T
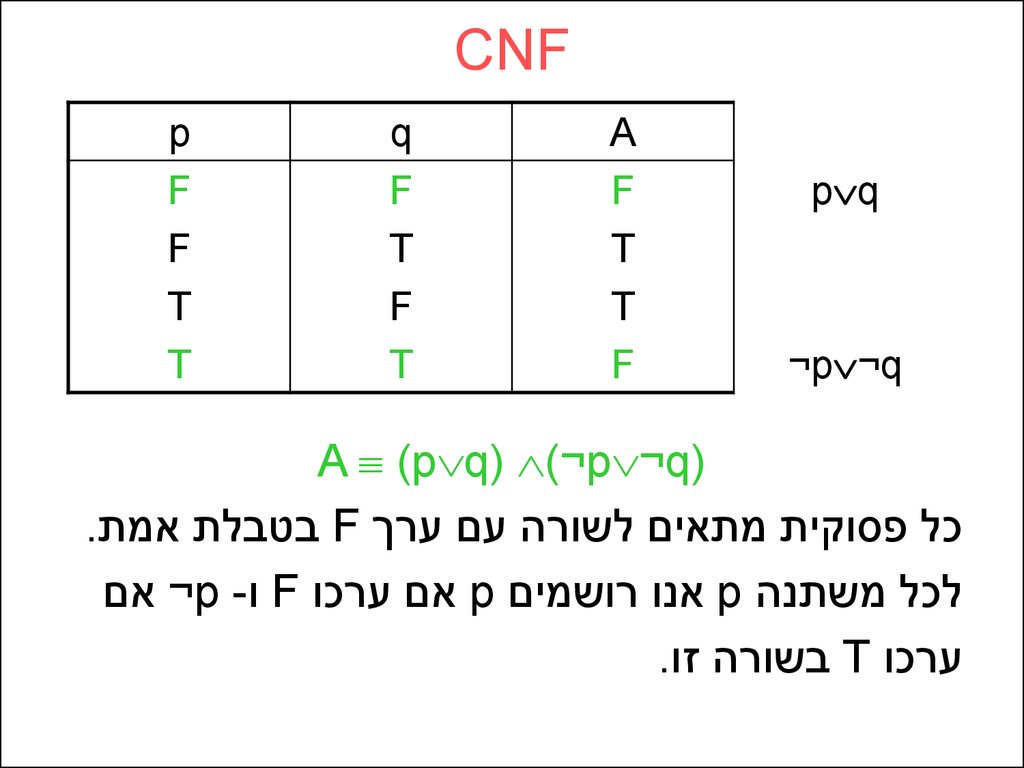
)A (p q) (¬p ¬q
כל פסוקית מתאים לשורה עם ערך Fבטבלת אמת.
לכל משתנה pאנו רושמים pאם ערכו Fו ¬p -אם
ערכו Tבשורה זו.
33.
CNF- וDNF אלגוריתמים לבניית; - ו • סילוק
(NNF • הכנסת שלילה פנימה (צורת
. או • פריסה של
((p q) ¬)q r)) s
.דוגמה
¬))p q) ¬)q r)) s
(¬)p q) (q r)) s
((¬p ¬q( (q r)) s
(¬p ¬q s) ((q r) s)
(¬p ¬q s) (q s) (r s)
34.
פסוקיות הורןפסוקית הורן ) (Horn clauseהיא פסוקית שמכילה
לא יותר מליטרל חיובי אחד.
) p ¬q1 ... ¬qn ( (q1 ... qn) p
) ¬q1 ... ¬qn ( (q1 ... qn)
)p ( T p
נוסחת הורן היא קוניונקציה של פסוקיות הורן.
35.
אלגוריתם הכרעה לנוסחאות הורןאלגוריתם HORNלהכרעת ספיקות:
נסמן אטומים בנוסחת הורן לפי כללים הבאים:
.1נסמן Tאם הוא קיים בנוסחה.
.2אם יש פסוקית (Q1 ... Qn) Pבנוסחה כך
שכל Qiבו מסומן ,נסמן גם Pונחזור ל ,2-אחרת
נעבור ל.3-
.3הנוסחה היא ספיקה אם ורק אם לא מסומן.
36.
משפט .אלגוריתם HORNמכריע בעיית ספיקות לנוסחאותהורן.
הוכחה .אם בנוסחת הורן Aיש nאטומים ,האלגוריתם מסיים
בלא יותר מ (n+1)-צעדים .נוכיח:
כל Pמסומן הוא אמיתי בכל מודל של Aבאינדוקציה על מספר
הצעדים של האלגוריתם .בסיס (צעד T :)1אמיתי בכל מודל.
אם בפסוקית (Q1 ... Qn) Pכל Qiמסומן ,אז גם הפסוקית
וגם כל ( Qiבהנחת אינדוקציה) חייבים להיות אמיתיים בכל
מודל של .Aלכן גם Pחייב להיות אמיתי בכל מודל של .]?[A
(א) אם מסומן A ,לא ספיקה ,כי לא יכול להיות אמיתי.
(ב) אם לא מסומן ,נגדיר פירוש lשבו האטומים המסומנים,
ורק הם ,אמיתיים .נניח ש l-הוא לא מודל של .Aאז קיימת
פסוקית (Q1 ... Qn) Pשל Aשהיא שקרית ב.l -אבל זה
אפשרי רק כאשר כל Qiאמיתי (מסומן) ו P-שקרי (לא מסומן)
– סתירה[?] .לכן lהוא מודל של Aומכאן Aספיקה.


























 informatics
informatics

