419.06K

Category:

economics

Микроэкономическое моделирование технологии производства и процессов потребления

1.

Тема 1.
Микроэкономическое моделирование
технологии производства
и процессов потребления

Аксиомы рациональности поведения потребителя
Обычно от ординалистской, или порядковой, функции
предпочтений экономического субъекта требуют, чтобы
она представляла собой отношение полного предпорядка
(или т.н. «слабое упорядочение»), т.е. удовлетворяла
следующим свойствам рационального выбора.
Первое свойство – это сравнимость любых возможных
вариантов организации хозяйственной деятельности, или
полнота данного множества: для любых вариантов x1 и x2
верно
либо
Второе свойство – это транзитивность отношения
упорядоченности: если для любых наборов x1, x2 и x3
и
, то

3.

Теорема Дебре
Теорема Дебре в слабой форме
Если множество X качественно сравнимых наборов благ, которое
должно быть замкнутым подмножеством пространства
действительных чисел, представляет собой отношение полного
предпорядка, т.е. удовлетворяет свойствам рациональности, и в
добавление к этому данный индикатор потребительских
предпочтений обладает свойствами непрерывности и строгой
глобальной ненасыщаемости, то ему соответствует количественная,
числовая функция полезности, которая при этом будет
непрерывной.
Теорема Дебре в сильной форме
Если множество X качественно сравнимых наборов благ, которое
должно быть замкнутым подмножеством пространства
действительных чисел, представляет собой отношение полного
предпорядка и данный ординалистский индикатор потребительских
предпочтений является непрерывным, то ему соответствует
непрерывная кардиналистская функция полезности.

4.

Отдача от масштаба и делимость производства 1, 1
Эквивалентные понятия:
Отдача от масштаба
Делимость
производства
Возрастающая
f x K , x L f x K , x L
f x K , x L f x K , x L Несовершенная
Постоянная
f x K , x L f x K , x L
f x K , x L f x K , x L «Пропорциональная»
Убывающая
f x K , x L f x K , x L
f x K , x L f x K , x L Совершенная
Эквивалентность возрастающей отдачи от масштаба и
несовершенной делимости производства:
f x K , x L f x K , x L
1
1; K xK , L xL
f K , L
f K , L
f K , L f K , L

5.

Отдача от масштаба и поведение средних издержек
TC(y)=TC(xK,xL)
y=f(x)
Факторизация издержек:
TC ( y ) TC f x K , x L TC x K , x L pK x K pL x L
x=(xK,xL)
Линейная однородность функции издержек от затрат факторов:
TC f xK , xL TC xK , xL pK xK pL xL
pK xK pL xL TC xK , xL TC f xK , xL
Возрастающая отдача от масштаба производства:
1
f x K , x L f x K , x L
Издержки – это возрастающая функция от объема производства:
TC f x K , x L TC f x K , x L TC f xK , x L
Итак, при положительном эффекте масштаба: TC y TC y
Средние издержки – убывающая функция объема производства:
TC y TC y TC y
AC y
AC y
y
y
y

6.

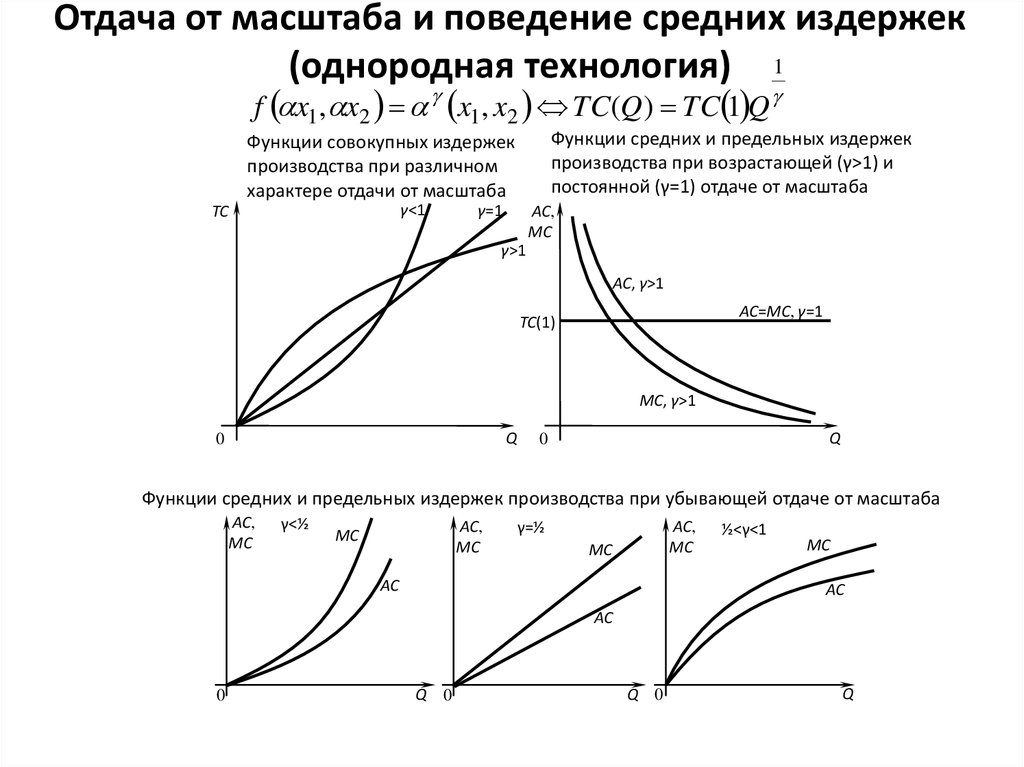
Отдача от масштаба и поведение средних издержек
(однородная технология)
Функция называется однородной степени γ, если для нее выполняется равенство
f(αx1,αx2)=αγf(x1,x2), где α, γ – положительные действительные константы.
При γ>1 следует положительный эффект масштаба и несовершенная делимость
производства; γ=1 дает постоянную отдачу от масштаба и пропорциональную
делимость; а в случае γ<1 наблюдается отрицательный эффект масштаба и
совершенная делимость хозяйственных операций.
Теорема Эйлера об однородных функциях: f ( x1 , x2 ) x1 f ( x1 , x2 ) x2 f ( x1 , x2 )
x1
x2
Домножим левую и правую части равенства на множитель Лагранжа λ:
f ( x1 , x2 )
f ( x1 , x2 )
x1
x2 f ( x1 , x2 )
x1
x2
Используем условия минимизации издержек: p1x1+p2x2=λγf(x1,x2).
В силу того, что множитель Лагранжа λ в задаче минимизации издержек
представляет собой их предельную величину, получаем дифференциальное
dTC
уравнение:
TC (Q)
Q
dQ
1
Его решением является функция издержек TC(Q) TC 1 Q

7.

Отдача от масштаба и поведение средних издержек
(однородная технология) 1
Справедливо и обратное утверждение. Пусть TC(Q) TC 1 Q
Функция издержек линейно однородна относительно затрат факторов:
TC(αx1,αx2)=p1αx1+p2αx2=α(p1x1+p2x2)=αTC(x1,x2)
1
1
В нашем случае: TC x1 , x2 TC(1) f x1, x2 TC x1, x2 TC(1) f x1 , x2 .
1
1
Итак: TC(1) f x1 , x2 TC(1) f x1 , x2 . Следовательно, f(αx1,αx2)=αγf(x1,x2).
1
Таким образом, функция издержек имеет степенной вид TC(Q) TC 1 Q
тогда и только тогда, когда производственная функция является однородной
степени γ: f(αx1,αx2)=αγf(x1,x2).

8.

Отдача от масштаба и поведение средних издержек
(однородная технология) 1
f x1 , x2 x1 , x2 TC(Q ) TC 1 Q
Функции средних и предельных издержек
производства при возрастающей (γ>1) и
постоянной (γ=1) отдаче от масштаба
Функции совокупных издержек
производства при различном
характере отдачи от масштаба
γ<1
TC
γ=1
AC,
MC
γ>1
AC, γ>1
AC=MC, γ=1
TC(1)
MC, γ>1
Q
0
Q
0
Функции средних и предельных издержек производства при убывающей отдаче от масштаба
AC,
MC
γ<½
AC,
MC
MC
AC,
MC
γ=½
MC
AC
½<γ<1
MC
AC
AC
0
Q 0
Q 0
Q

9.

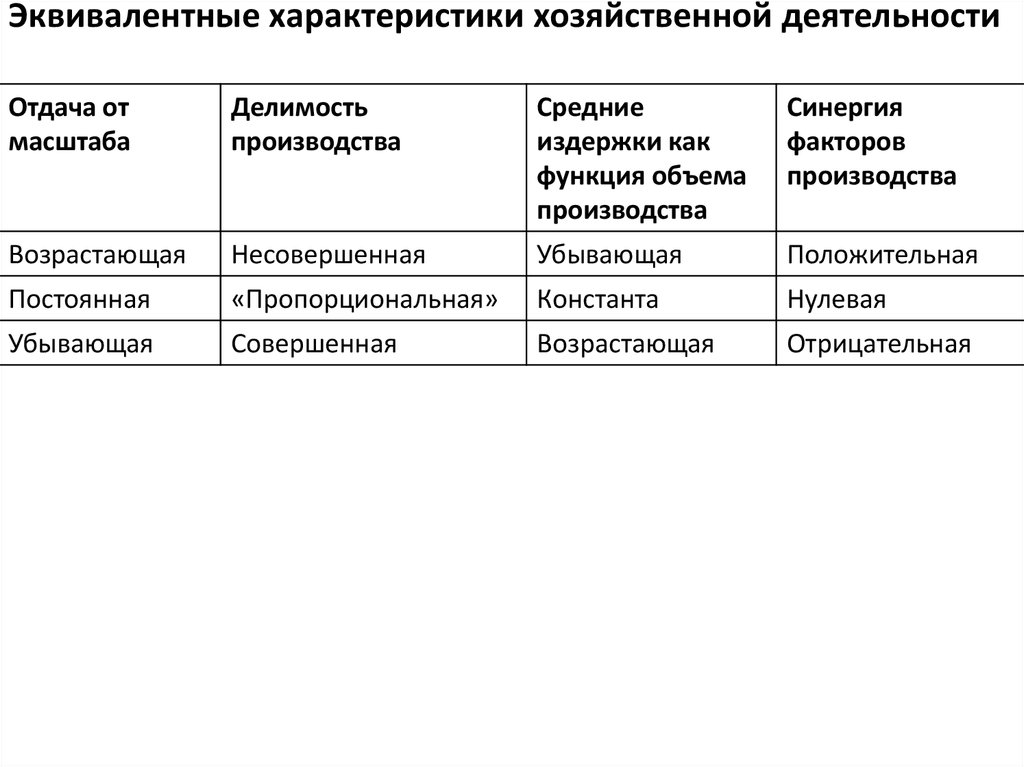
Эквивалентные характеристики хозяйственной деятельности
Отдача от
масштаба
Делимость
производства
Средние
издержки как
функция объема
производства
Синергия
факторов
производства
Возрастающая
Несовершенная
Убывающая
Положительная
Постоянная
«Пропорциональная»
Константа
Нулевая
Убывающая
Совершенная
Возрастающая
Отрицательная

10.

Выпуклые функции
(η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2)
y=f(x)
Y
В пространстве R X
(η,x2)
f(x1)=
множество
gr , x R X f ( x )
f(x2)=η
(f(x), x) называется графиком
f(x)
XK множество
(η,x1)
epigr , x R X f ( x )
называется надграфиком
x2
множество
0
opigr q, x R X f ( x ) q
x=λx1+(1–λ)x2
называется подграфиком,
x1
или технологическим
XL
множеством функции
f : X R
Множество x f ( x ) q, q R называется изоквантой (кривой
безразличия)
Множество x f ( x ) q, q R называется верхним лебеговским
Множество x f ( x ) , R называется нижним лебеговским
для функции f : X R

11.

Выпуклые функции
Y
f(x1)=
f(x2)=η
y=f(x)
(η,x2)
(η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2)
Множество X называется
выпуклым, если для
произвольных векторов x1 и
(f(x), x)
x2 из X любой вектор x,
f(x)
XK лежащий на соединяющем их
(η,x1)
отрезке, так же принадлежит
x2
этому множеству:
x1, x2 X x x1 (1 ) x2 X ,
0
R, [0,1]
x=λx1+(1–λ)x2
Функция f : X R называется
x1
Функция f : X R
выпуклой, если ее надграфик –
XL это выпуклое множество:
является выпуклой тогда
и только тогда, когда ее
f x1 (1 ) x2 f x1 (1 ) f x2 ;
второй дифференциал
x1, x2 X , R, [0,1]
неотрицателен:
2
2
2
f
x
,
x
f
x
,
x
f xK , xL 2
2
K L
K L
d2y
dx
2
dx
dx
dxL 0
K
K
L
2
2
x K x L
x K
x L

12.

Выпуклые функции
y=f(x)
(η,x2)
Y
f(x1)=
f(x2)=η
f(x)
(η,x1)
Следовательно, функция
f : X R является выпуклой
(f(x), x) тогда и только тогда, когда
XK главные миноры ее матрицы
Гессе
x2
0
x=λx1+(1–λ)x2
(η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2)
x1
XL
2 f xK , xL 2 f xK , xL
2
x K x L
x K
2 f x , x 2 f x , x
K L
K L
2
x
x
x
L K
L
- неотрицательные:
f xK , xL
f xK , xL f xK , xL f xK , xL
0,
2
2
2
x
x
x K
x K
x L
K
L
2
2
2
2
2

13.

Выпуклые функции
y=f(x)
(η,x2)
Y
f(x1)=
f(x2)=η
f(x)
(η,x1)
x2
0
x=λx1+(1–λ)x2
x1
Функция f : X R
является строго выпуклой
тогда и только тогда, когда
ее второй дифференциал
положителен:
(η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2)
Функция f : X R
(f(x), x) называется строго выпуклой,
XK если ее надграфик – это
выпуклое множество и при
этом для любых двух точек ,
принадлежащих графику
функции, никакая внутренняя
точка соединяющего их
отрезка не принадлежит
XL
графику :
f x1 (1 ) x2 f x1 (1 ) f x2 ;
x1, x2 X , R, (0,1)
2
2
2
f
x
,
x
f
x
,
x
f xK , xL 2
2
K L
K L
d2y
dx
2
dx
dx
dxL 0
K
K
L
2
2
x K x L
x K
x L

14.

Выпуклые функции
y=f(x)
(η,x2)
Y
f(x1)=
f(x2)=η
f(x)
(η,x1)
Следовательно, функция
f : X R является строго
(f(x), x) выпуклой тогда и только
XK тогда, когда главные миноры
ее матрицы Гессе
x2
0
x=λx1+(1–λ)x2
(η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2)
x1
XL
2 f xK , xL 2 f xK , xL
2
x K x L
x K
2 f x , x 2 f x , x
K L
K L
2
x
x
x
L K
L
- положительные:
f xK , xL
f xK , xL f xK , xL f xK , xL
0,
2
2
2
x
x
x K
x K
x L
K
L
2
2
2
2
2

15.

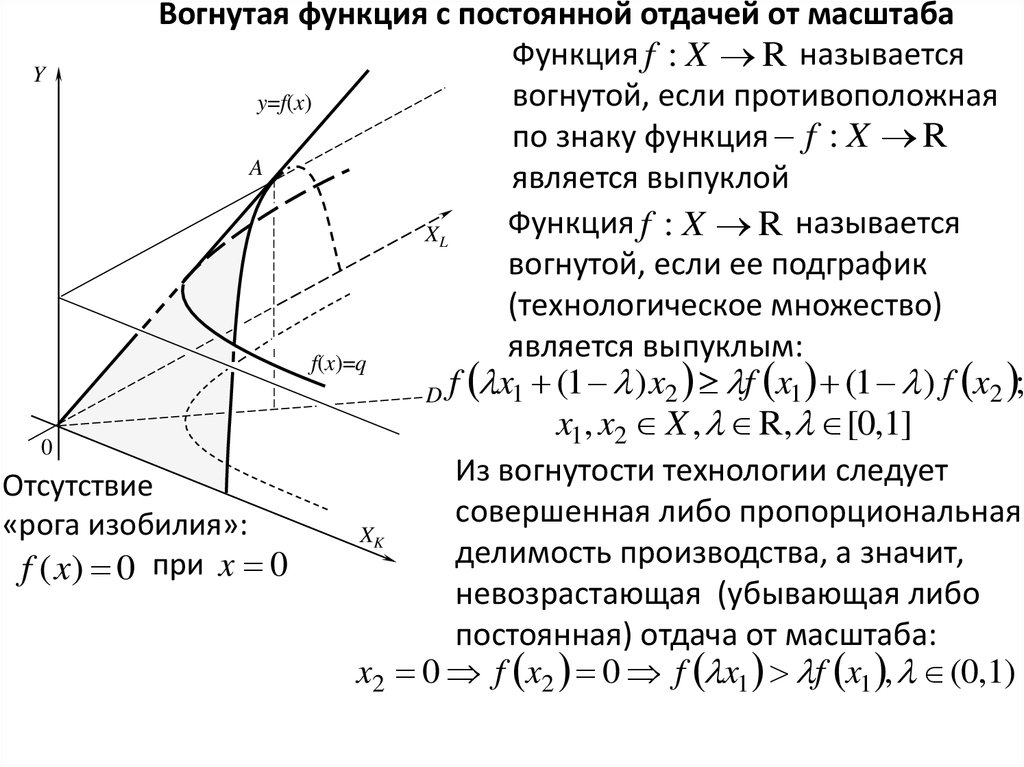
Вогнутая функция с постоянной отдачей от масштаба
Функция f : X R называется
Y
вогнутой, если противоположная
y=f(x)
по знаку функция f : X R
A
является выпуклой
Функция f : X R называется
XL
вогнутой, если ее подграфик
(технологическое множество)
является выпуклым:
f(x)=q
D f x1 (1 ) x2 f x1 (1 ) f x2 ;
x1, x2 X , R, [0,1]
0
Из вогнутости технологии следует
Отсутствие
совершенная либо пропорциональная
«рога изобилия»:
XK
делимость производства, а значит,
f ( x) 0 при x 0
невозрастающая (убывающая либо
постоянная) отдача от масштаба:
x2 0 f x2 0 f x1 f x1 , (0,1)

16.

Y
0
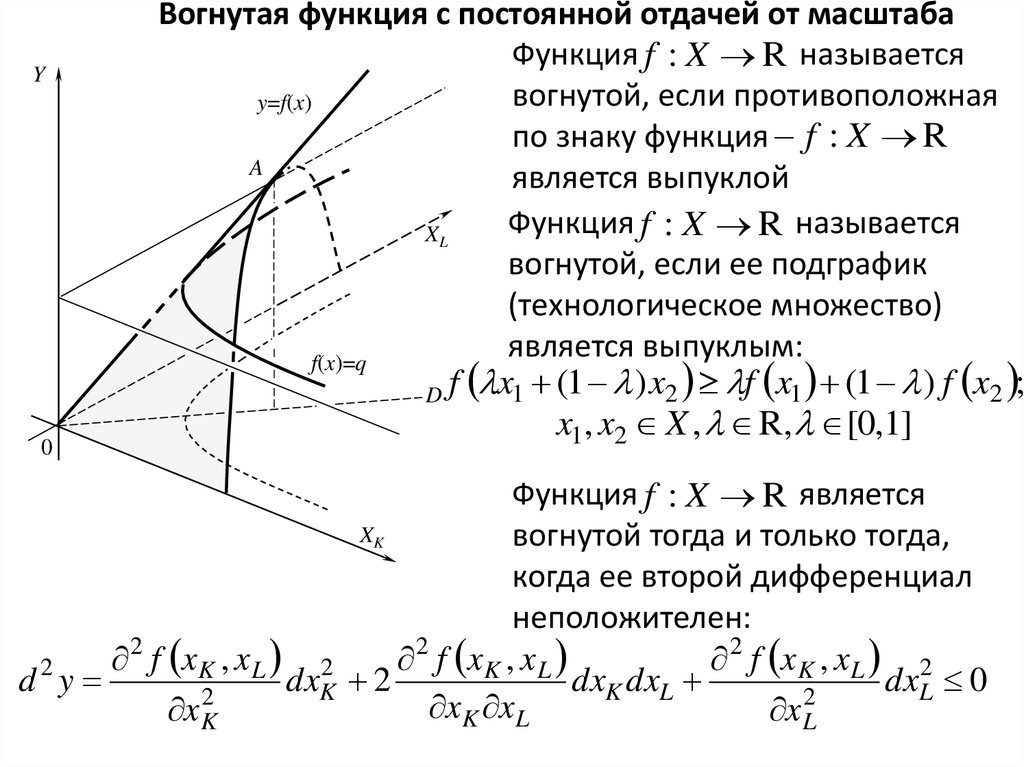
Вогнутая функция с постоянной отдачей от масштаба
Функция f : X R называется
вогнутой, если противоположная
y=f(x)
по знаку функция f : X R
A
является выпуклой
Функция f : X R называется
XL
вогнутой, если ее подграфик
(технологическое множество)
является выпуклым:
f(x)=q
D f x1 (1 ) x2 f x1 (1 ) f x2 ;
x1, x2 X , R, [0,1]
XK
Функция f : X R является
вогнутой тогда и только тогда,
когда ее второй дифференциал
неположителен:
2
2
2
f
x
,
x
f
x
,
x
f xK , xL 2
2
2
K L
K L
d y
dxK 2
dxK dxL
dxL 0
2
2
x K x L
x K
x L

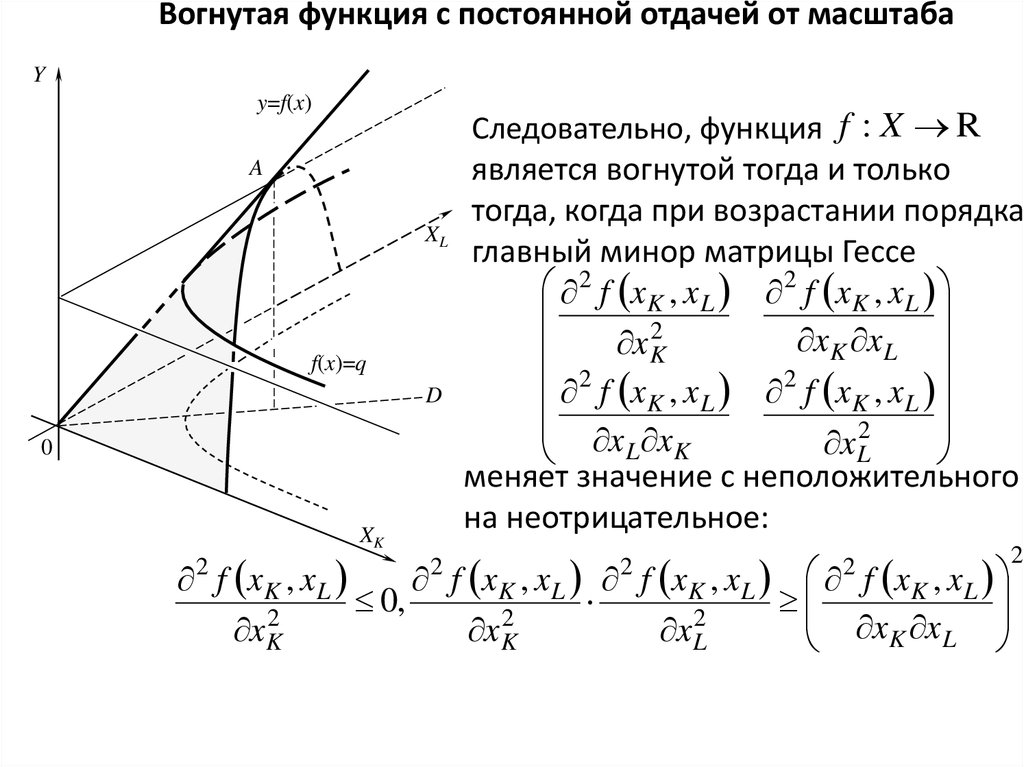
17.

Вогнутая функция с постоянной отдачей от масштаба
Y
y=f(x)
A
XL
f(x)=q
D
0
XK
Следовательно, функция f : X R
является вогнутой тогда и только
тогда, когда при возрастании порядка
главный минор матрицы Гессе
2 f xK , xL 2 f xK , xL
2
x K x L
x K
2 f x , x 2 f x , x
K L
K L
2
x
x
x
L
K
L
меняет значение с неположительного
на неотрицательное:
f xK , xL
f xK , xL f xK , xL f xK , xL
0,
2
2
2
x
x
x K
x K
x L
K
L
2
2
2
2
2

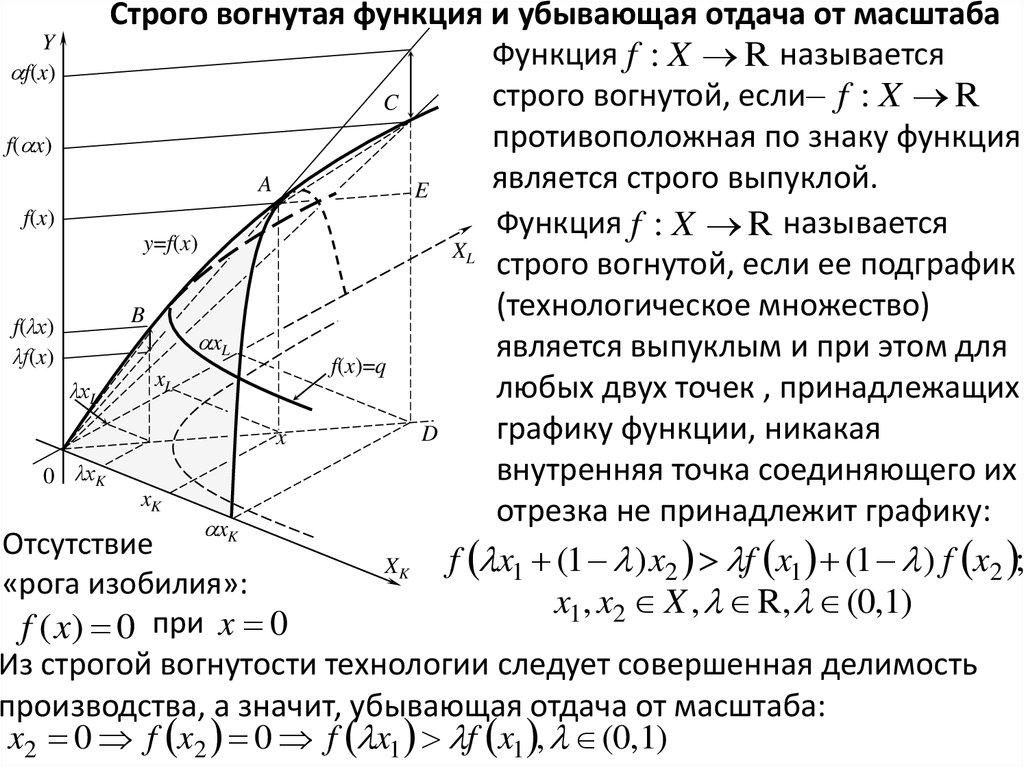
18.

Строго вогнутая функция и убывающая отдача от масштаба
Y
Функция f : X R называется
f(x)
строго вогнутой, если f : X R
C
противоположная по знаку функция
f( x)
является строго выпуклой.
A
E
f(x)
Функция f : X R называется
y=f(x)
XL
строго вогнутой, если ее подграфик
(технологическое множество)
B
f(λx)
xL
является выпуклым и при этом для
λf(x)
f(x)=q
xL
любых двух точек , принадлежащих
λxL
графику функции, никакая
D
x
внутренняя точка соединяющего их
0 λxK
xK
отрезка не принадлежит графику:
xK
Отсутствие
f x1 (1 ) x2 f x1 (1 ) f x2 ;
XK
«рога изобилия»:
x1, x2 X , R, (0,1)
f ( x) 0 при x 0
Из строгой вогнутости технологии следует совершенная делимость
производства, а значит, убывающая отдача от масштаба:
x2 0 f x2 0 f x1 f x1 , (0,1)

19.

Строго вогнутая функция и убывающая отдача от масштаба
Y
Функция f : X R называется
f(x)
строго вогнутой, если ее подграфик
C
(технологическое множество)
f( x)
является выпуклым и при этом для
A
E
f(x)
любых двух точек , принадлежащих
y=f(x)
XL
графику функции, никакая
внутренняя точка соединяющего их
B
f(λx)
xL
отрезка не принадлежит графику:
λf(x)
f(x)=q
xL
λxL
f x1 (1 ) x2 f x1 (1 ) f x2 ;
D
x
x1, x2 X , R, (0,1)
0 λxK
Функция f : X R является
xK
строго вогнутой тогда и только
xK
тогда, когда ее второй
XK
дифференциал отрицателен:
2
2
2
f
x
,
x
f
x
,
x
f xK , xL 2
2
2
K L
K L
d y
dxK 2
dxK dxL
dxL 0
2
2
x K x L
x K
x L

20.

Строго вогнутая функция и убывающая отдача от масштаба
Y
f(x)
C
f( x)
A
E
f(x)
y=f(x)
2 f xK , xL 2 f xK , xL
xL
2
f(x)=q
x K x L
x K
xL
2 f x , x 2 f x , x
K L
K L
D
x
2
x
x
x
L K
L
xK
меняет значение с отрицательного
xK
на положительное:
XK
2
2
2
2
2
f xK , xL
f xK , xL f xK , xL f xK , xL
0,
2
2
2
x
x
x K
x K
x L
K
L
B
f(λx)
λf(x)
λxL
0 λxK
XL
Следовательно, функция f : X R
является строго вогнутой
тогда и только тогда, когда
при возрастании порядка
главный минор матрицы Гессе

21.

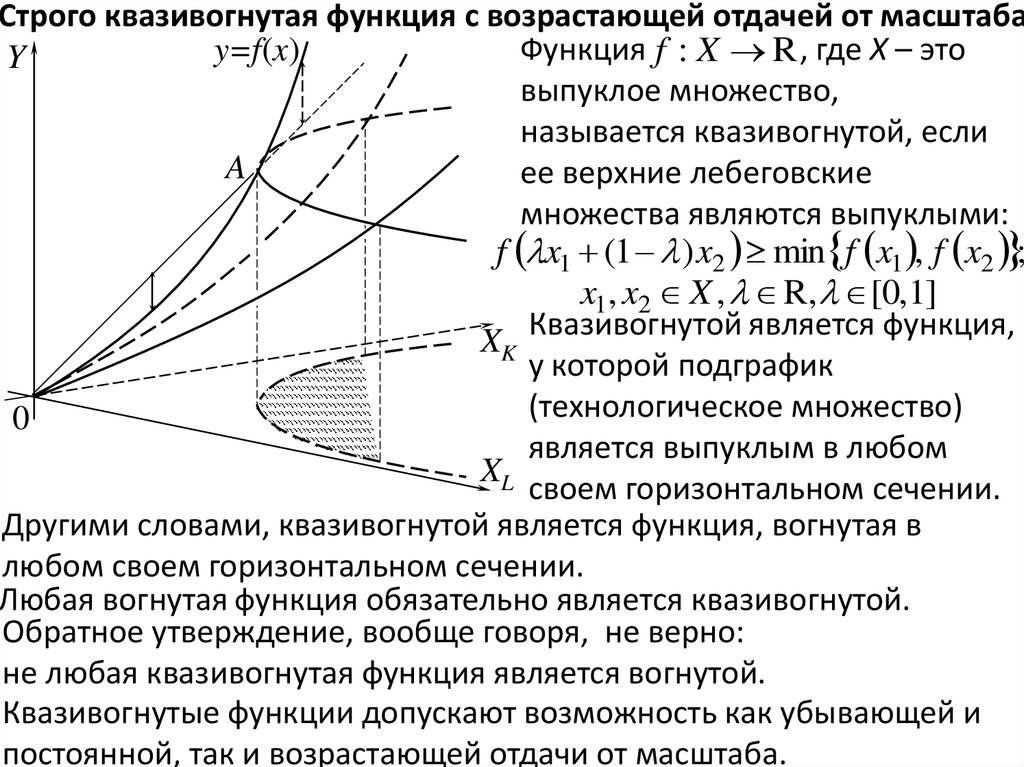
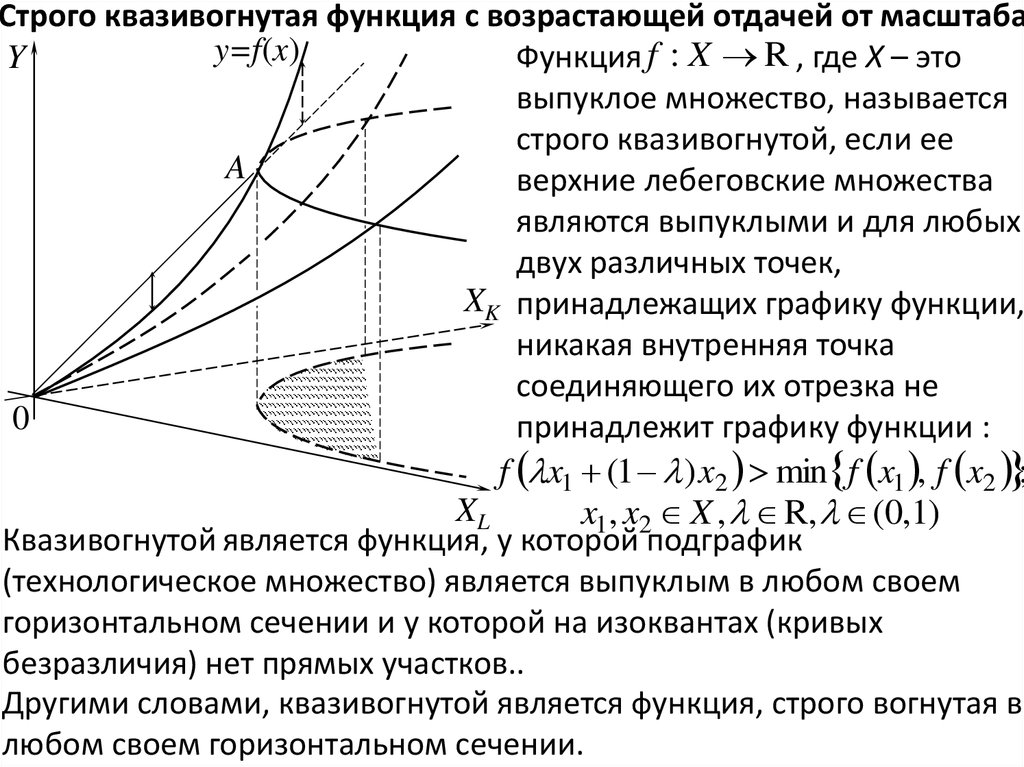
Строго квазивогнутая функция с возрастающей отдачей от масштаба
Функция f : X R , где X – это
y=f(x)
Y
выпуклое множество,
называется квазивогнутой, если
A
ее верхние лебеговские
множества являются выпуклыми:
f x1 (1 ) x2 min f x1 , f x2 ;
x1, x2 X , R, [0,1]
Квазивогнутой является функция,
XK
у которой подграфик
(технологическое множество)
0
является выпуклым в любом
XL
своем горизонтальном сечении.
Другими словами, квазивогнутой является функция, вогнутая в
любом своем горизонтальном сечении.
Любая вогнутая функция обязательно является квазивогнутой.
Обратное утверждение, вообще говоря, не верно:
не любая квазивогнутая функция является вогнутой.
Квазивогнутые функции допускают возможность как убывающей и
постоянной, так и возрастающей отдачи от масштаба.

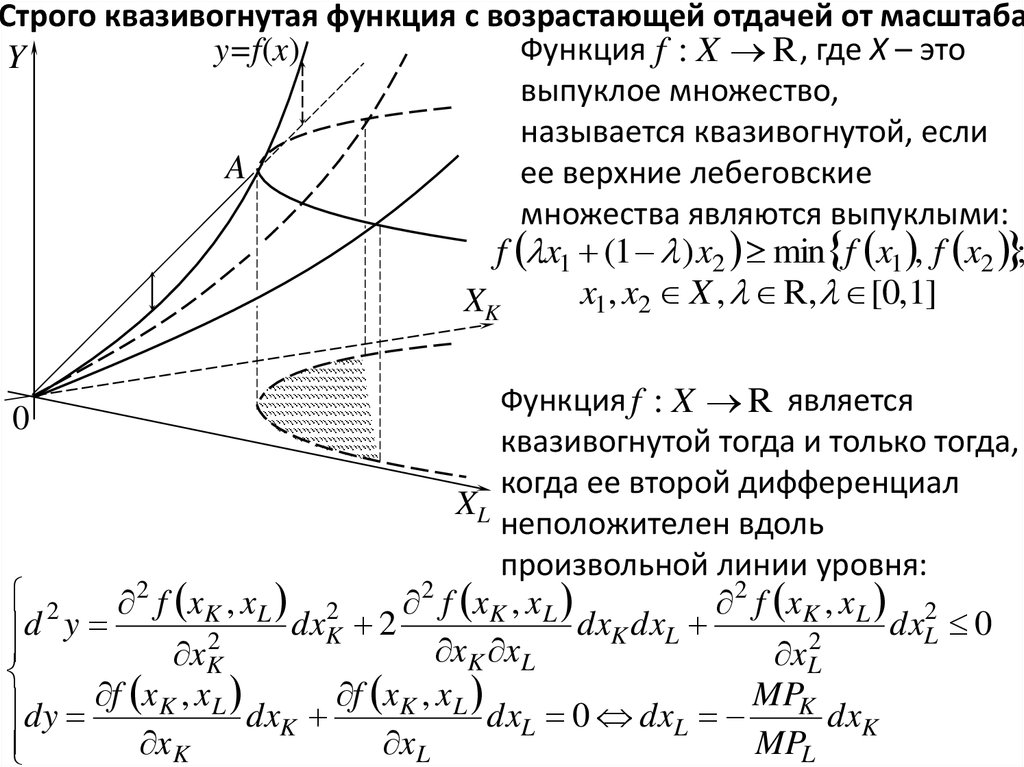
22.

23.

24.

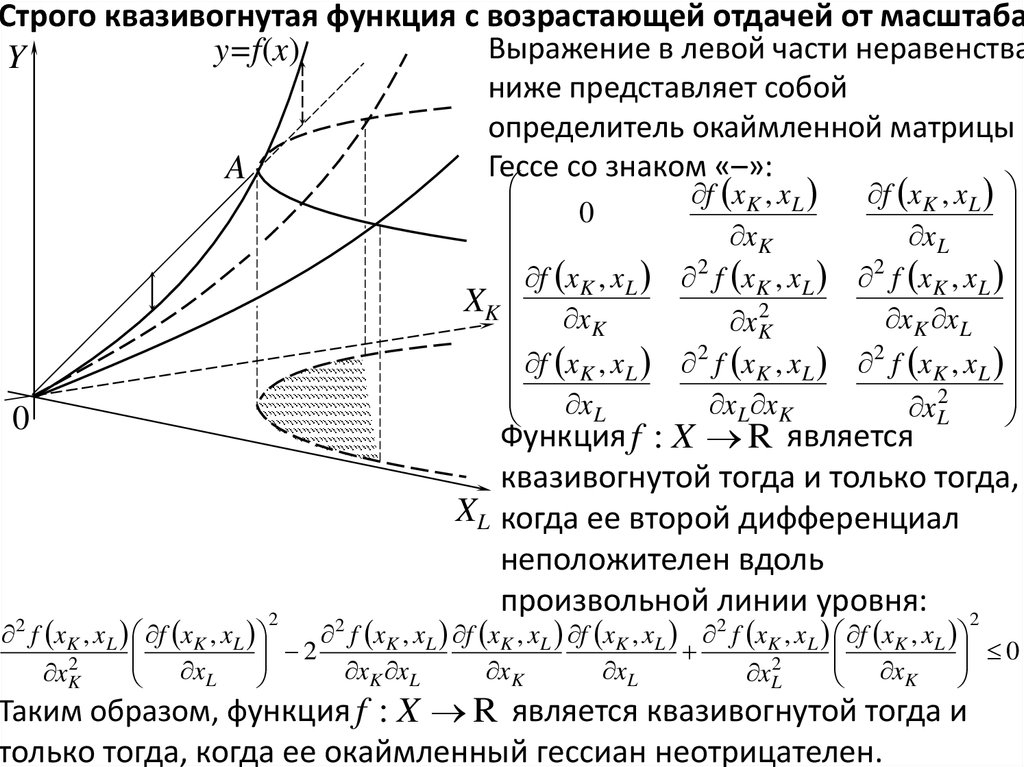
Строго квазивогнутая функция с возрастающей отдачей от масштаба
Выражение в левой части неравенства
y=f(x)
Y
ниже представляет собой
определитель окаймленной матрицы
Гессе со знаком «–»:
A
f
x
,
x
f
x
,
x
K
L
K
L
0
x K
x L
f x , x 2 f x , x 2 f x , x
K L
K L
K L
XK
x K x L
x K2
x K
f x , x 2 f x , x 2 f x , x
K L
K L
K L
2
x L
x L x K
x L
0
Функция f : X R является
квазивогнутой тогда и только тогда,
XL когда ее второй дифференциал
неположителен вдоль
произвольной линии уровня: 2
2
2
2
f xK , xL f xK , xL
f xK , xL f xK , xL f xK , xL 2 f xK , xL f xK , xL
2
0
xK2
xL
xK xL
xK
xL
xL2
xK
Таким образом, функция f : X R является квазивогнутой тогда и
только тогда, когда ее окаймленный гессиан неотрицателен.

25.

Строго квазивогнутая функция с возрастающей отдачей от масштаба
y=f(x)
Функция f : X R , где X – это
Y
выпуклое множество, называется
строго квазивогнутой, если ее
A
верхние лебеговские множества
являются выпуклыми и для любых
двух различных точек,
XK принадлежащих графику функции,
никакая внутренняя точка
соединяющего их отрезка не
0
принадлежит графику функции :
f x1 (1 ) x2 min f x1 , f x2 ;
XL
x1, x2 X , R, (0,1)
Квазивогнутой является функция, у которой подграфик
(технологическое множество) является выпуклым в любом своем
горизонтальном сечении и у которой на изоквантах (кривых
безразличия) нет прямых участков..
Другими словами, квазивогнутой является функция, строго вогнутая в
любом своем горизонтальном сечении.

26.

Строго квазивогнутая функция с возрастающей отдачей от масштаба
y=f(x)
Функция f : X R , где X – это
Y
выпуклое множество, называется
строго квазивогнутой, если ее
A
верхние лебеговские множества
являются выпуклыми и для любых
двух различных точек,
XK принадлежащих графику функции,
никакая внутренняя точка
соединяющего их отрезка не
0
принадлежит графику функции :
f x1 (1 ) x2 min f x1 , f x2 ;
XL
x1, x2 X , R, (0,1)
Любая строго вогнутая функция обязательно является строго
квазивогнутой.
Обратное утверждение, вообще говоря, не верно: не любая строго
квазивогнутая функция является строго вогнутой.
Строго квазивогнутые функции допускают возможность любого типа
(убывающего, постоянного и возрастающего) эффекта масштаба.

27.

Строго квазивогнутая функция с возрастающей отдачей от масштаба
y=f(x)
Y
A
XK
0
XL
Функция f : X R является
строго квазивогнутой тогда и
только тогда, когда ее второй
дифференциал отрицателен
вдоль произвольной линии
уровня:
2
2 f xK , xL 2
2 f xK , xL
2 f xK , xL 2
dxK 2
dxK dxL
dxL 0
d y
2
2
x K x L
x K
x L
dy f x K , x L dxK f x K , x L dxL 0 dxL MPK dxK
x K
x K
MPL

28.

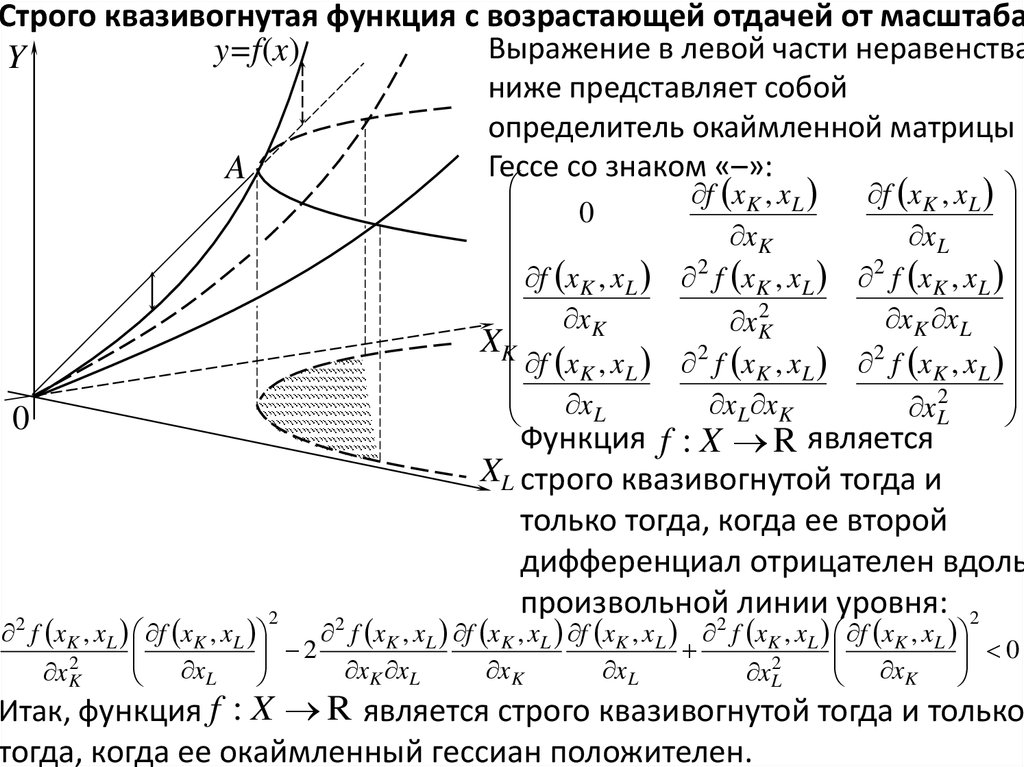
Строго квазивогнутая функция с возрастающей отдачей от масштаба
Выражение в левой части неравенства
y=f(x)
Y
ниже представляет собой
определитель окаймленной матрицы
Гессе со знаком «–»:
A
f
x
,
x
f
x
,
x
K
L
K
L
0
x K
x L
f x , x 2 f x , x 2 f x , x
K L
K L
K L
x K x L
x K2
x K
XK
f x K , x L 2 f x K , x L 2 f x K , x L
2
x L
x L x K
x L
0
Функция f : X R является
XL строго квазивогнутой тогда и
только тогда, когда ее второй
дифференциал отрицателен вдоль
произвольной линии уровня: 2
2
2
2
f xK , xL f xK , xL
f xK , xL f xK , xL f xK , xL 2 f xK , xL f xK , xL
2
0
xK2
xL
xK xL
xK
xL
xL2
xK
Итак, функция f : X R является строго квазивогнутой тогда и только
тогда, когда ее окаймленный гессиан положителен.

29.

Строго квазивогнутая функция с возрастающей отдачей от масштаба
y=f(x)
Свойства неоклассических
Y
производственных функций
(функций полезности):
A
y f xK , xL C 2
XK
0
f x K , x L
f x K , x L
0,
0
x K
x L
2 f xK , xL
2 f xK , xL
0,
0
2
2
x K
x L
2 f xK , xL 2 f xK , xL
0
x K x L
x L x K
XL
f xK , x L
f xK , xL
dy
dx
dxL 0
Вдоль изокванты:
K
x K
xL
dxL
MPK
0
Следовательно:
dxK y const
MPL
2 f x K , x L f x K , x L
2 f x K , x L f x K , x L f x K , x L 2 f x K , x L f x K , x L
2
2
2
x
x
x
x
x
x
x K
x L
L
K L
K
L
K
2
d
dxK
dxL
dxK
y const
f x K , x L
x
L
3
2
0

English Русский Rules