Similar presentations:
Комбинаторика. Свойства сочетаний. (Лекция 11)
1. Комбинаторика
12. Сочетания
• Определение 1• k-сочетанием множества А называется неупорядоченный набор
попарно различных элементов множества А длины k. Другими
словами k-сочетание – это k-элементное подмножество
множества А
A a; b; c . 2- сочетания: {a; b};{a; c};{b; c}
• Пример:
• Число k- сочетаний n-элементного множества обозначается C nk
и вычисляется по формуле
C nk
n!
k!(n k )!
2
3. Свойства сочетаний
1) С nk C nn kДоказательство:
Сnk
Сnn k
n!
k!(n k )!
n!
n!
(n k )!(n (n k ))! (n k )! k!
Cnk Cnn k
2) C nk 11 C nk 1 C nk
Доказательство:
Сnk 11
(n 1)!
(n 1)!
(k 1)!(n 1 (k 1))! (k 1)!(n k )!
Сnk 1 Cnk
n!
n!
n!(n k ) n!(k 1)
n!(n 1)
(n 1)!
(k 1)!(n k 1)! k!(n k )!
(k 1)!(n k )!
(k 1)!(n k )! (k 1)!(n k )!
3
4. Свойства сочетаний
n(а b) C nk a n k b k
n
3) Бином Ньютона:
k 0
Доказать самостоятельно (5 баллов)
Следствия из бинома Ньютона:
n
Равенство
C
k 0
k
n
2n
n
Равенство
( 1)
k 0
k
получается из бинома Ньютона при a b 1
C nk 0 получается из бинома Ньютона при a 1, b 1
4
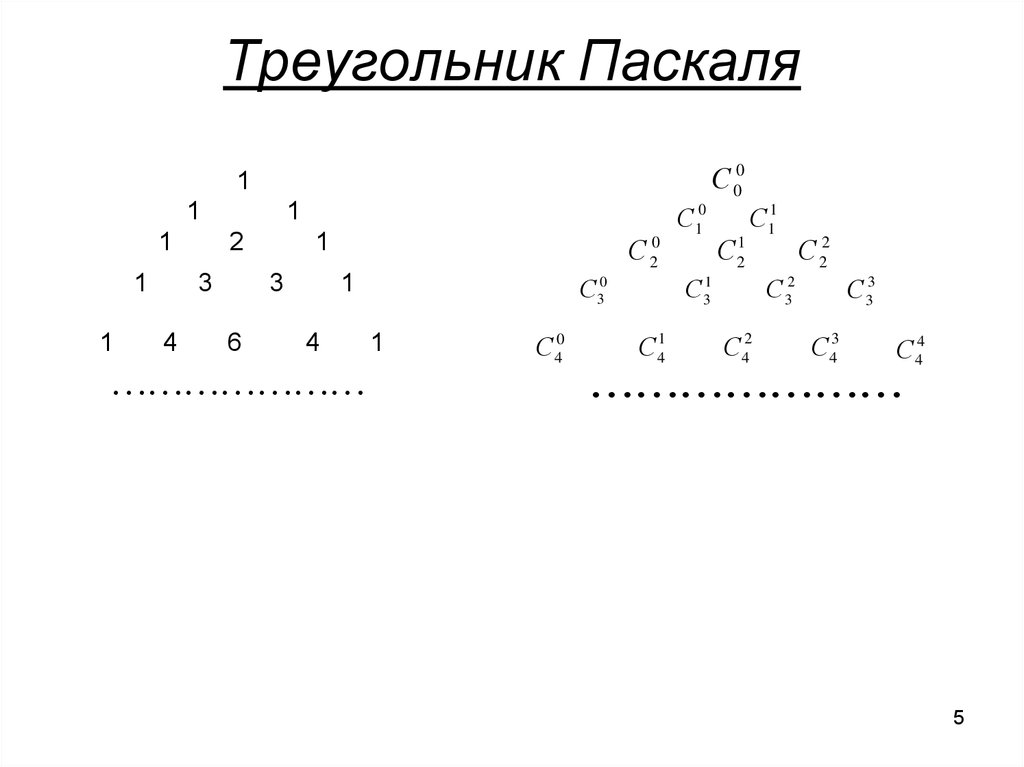
5. Треугольник Паскаля
С 001
1
1
1
1
1
2
3
4
1
3
6
С 20
1
4
С30
1
С40
С10
С 21
С11
С 31
С41
С 22
С 32
С42
С 33
С43
С44
5
6. Сочетание с повторениями
• Определение 5k-сочетанием с повторениями n элементного множества,
называется неупорядоченный набор элементов данного
множества длины k.
• Пример: А= a; b; c
2 сочетания с повторениями: a; b ; b; c ; a; c ; a; a ; b; b ; c; c
Число k-сочетание с повторениями n – элементного множества
обозначается:
C nk
6
7. Сочетания с повторениями
ТеоремаЧисло k-сочетание с повторениями n – элементного множества вычисляется
по формуле:
C nk C nk k 1
Доказательство:
Лемма. Число наборов из m нулей и n единиц равно
Cnn m
Закодируем k - сочетания с повторениями наборами из 0 и 1, отделяя нулями
группы элементов одного типа. Количество 1 равно k, а количество нулей
(n-1). Число таких кодов равно
Ckk n 1
7
8.
Сводная таблицаУпорядоченный
С повторениями
Аnk n k
P n (n1 , n2 ,..., nk )
Без повторений
Неупорядоченный
Ank
(n1 n2 ... nk )!
n1! n2 ! ... nk !
n!
n (n 1) (n k 1)
n k !
C nk C nk k 1
n!
C
k!(n k )!
k
n
Ann Pn n!
8
9. Задачи
• 1) В почтовом отделении продают 10 сортов открыток. Сколькимиспособами можно купить в нем 8 различных открыток? Сколькими
способами можно купить 8 открыток?
С108
С10 C108 8 1
8
10!
10! 10 9
45
8!(10 8)! 8! 2!
2
17!
17! 10 11 12 13 14 15 16 17
10 11 13 17 24310
8!(17 8)! 8! 9!
1 2 3 4 5 6 7 8
9
10. Задачи
• 2)Сколькими способами можно раздать 7 одинаковыхапельсинов между тремя детьми?
• Решение. Так как апельсины одинаковые, их вообще
нельзя использовать в качестве 7 различных элементов
множества.
Рассмотрим множество, состоящее из троих детей. Будем
выбирать детей для апельсинов. Используем формулу
числа сочетаний с повторениями, так как одному ребенку
может достаться несколько апельсинов, а может не
достаться ни одного.
7
3
C С77 3 1 С97
9! 8 9
36
7!2!
2
11. Задачи
• 3) Сколькими способами можно раздать 5 одинаковых апельсинов,3 банана, 7 яблок между 4 людьми?
С 4 С 4 С 4 С85 С63 С107
5
3
7
8! 6! 10! 6 7 8 4 5 6 8 9 10
56 20 120 134400
5!3! 3!3! 7!3!
6
6
6
11
12. Задачи
• 4) Сколькими способами можно закодировать дверь?1
10
C10
C102 C103 C104 C105 C106 C107 C108 C109 C10
210 1 1023
• 5) Сколько существует трехзначных чисел?
A10 A10 103 102 900
3
2
• 6) Абонент забыл последние 3 цифры телефонного номера.
Помня, что эти цифры различны, он набирает номер наугад.
Сколько номеров ему нужно перебрать, если он невезучий
человек?
A103
10!
8 9 10 720
10 3 !
12
13. Задачи
• 7)В группе 8 юношей и 9 девушек. Сколькимиспособами можно выбрать группу студентов,
состоящей из 4 юношей и 3 девушек?
• Решение. Четырех юношей выберем из 8, троих
девушек – из 9. По правилу умножения получим
С84 С93
8! 9!
70 84 5880
4!4! 3!6!
14. Задачи
• 8)Используя бином Ньютона, раскрыть скобки( a b) 5
.
• Решение.
(a b)5 C50 a 5b 0 C51a 4b1 C52 a 3b 2 C53a 2b3 C54 a1b 4 C55 a 0b5
a 5 5a 4b 10a 3b 2 10a 2b3 5ab 4 b5
15. Задачи
• 9) Сколькими способами можно распределить 5 одинаковыхпринтеров, 3 телефонных аппарата, 7 мониторов между 4
фирмами?
• Решение. Распределим сначала принтеры, затем телефонные
аппараты, и, наконец, мониторы. Используя правило умножения,
получим
С 4 С 4 С 4 С85 С63 С107
5
3
7
8! 6! 10! 6 7 8 4 5 6 8 9 10
56 20 120 134400
5!3! 3!3! 7!3!
6
6
6














 mathematics
mathematics








