Рассеяние характеристик прочности и нагруженности. Оценка показателей надежности: модель нагрузка-прочность

1.

Белорусский государственный университет транспорта
кафедра «ЛОКОМОТИВЫ»
ОСНОВЫ ТЕОРИИ НАДЕЖНОСТИ
Лектор: д.т.н., профессор Сосновский Леонид Адамович
к.т.н., доцент Комиссаров Виктор Владимирович
п.з.: ассистент Таранова Елена Сергеевна
Лекции – 18 часов
Практические занятия – 12 часов
Форма контроля знаний – зачет
(по всем вопросам обращаться на кафедру ауд. 1403,
а также в лабораторию ауд. 1415а)
ГОМЕЛЬ, 2017

2.

ЛИТЕРАТУРА
2
Основная:
1. Сосновский, Л.А. Элементы теории вероятностей, математической статистики и теории
надёжности / Л.А. Сосновский. – Гомель; БелГУТ, 1994. – 146 с. (в НТБ БелГУТа).
2. Шевченко Д.Н. Основы теории надежности : учеб.-методич. пособие для студ. техн. спец./
Д.Н. Шевченко; под ред. Л.А. Сосновского. – Гомель: БелГУТ, 2010. – 250 с. (в НТБ БелГУТа)
3. Богданович А.В. Оценка основных показателей надежности и риска невосстанавливаемых
изделий / А.В. Богданович, О.М. Еловой, Л.А. Сосновский. – Гомель : БелГУТ, 1995 г. – 95 с.
(в НТБ БелГУТа)
Дополнительная:
1. Сосновский, Л.А. Вероятностные методы расчета на прочность при линейном и сложном напряженных
состояниях в 2-х частях: Метод. указания по изучению курса «Сопротивление материалов»/ Л.А. Сосновский. –
Гомель: БелИИЖТ, 1984. – 74с. (в НТБ БелГУТа).
2. Сосновский, Л.А. L-риск (механотермодинамика необратимых повреждений) / Л.А. Сосновский. – Гомель:
БелГУТ, 2004. – 317 с.
3. Сосновский, Л.А. Комплексная оценка надежности силовых систем по критериям сопротивления усталости и
износостойкости (основы трибофатики): Метод. указания по изучению курса «Надежность транспортных
систем, машин и сооружений» для студентов транспортных вузов / Л.А. Сосновский. – Гомель: БелИИЖТ, 1988.
–56 с. (в НТБ БелГУТа ).
4. Богданович, А.В. Оценка надежности простого коленчатого вала. Надежность по критериям трибофатики:
Пособие по курсу «Основы теории надежности» / А.В. Богданович, О.М. Еловой, Л.А. Сосновский. – Гомель:
БелГУТ, 2002. – Ч.2.–30 с. (в методическом кабинете кафедры – 5 экз.).
5. Сосновский, Л.А. Показатель безопасности и оперативная характеристика риска / Л.А. Сосновский. – Гомель,
БелИИЖТ, 1991. (в НТБ БелГУТа).

3.

ПЛАН ЛЕКЦИЙ
3
Лекция 1. Надежность в технике
Лекция 2. Отказы и их причины. Статистический анализ
Лекция 3. Оценка показателей надежности: модель отказов
Лекция 4. Рассеяние характеристик прочности и нагруженности
Лекция 5. Оценка показателей надежности: модель нагрузка-прочность (часть1)
Лекция 6. Оценка показателей надежности: модель нагрузка-прочность (часть2)
Лекция 7. Схемная надежность
Лекция 8. Надежность трибофатической системы
Лекция 9. Концепция риска. Оценка безопасности.

4.

Лекция 4
РАССЕЯНИЕ ХАРАКТЕРИСТИК
ПРОЧНОСТИ И НАГРУЖЕННОСТИ.
ОЦЕНКА ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ:
МОДЕЛЬ НАГРУЗКА-ПРОЧНОСТЬ

5.

4.1 Рассеяние характеристик
прочности и нагруженности
а)
5
б)
Рисунок 1 – Результаты испытания на растяжение материалов
в хрупком (а) и вязком (б) состояниях

6.

4.1 Рассеяние характеристик
прочности и нагруженности
Рисунок 2 - Эмпирические функции распределения пределов текучести и
прочности, относительного сужения и истинного сопротивления разрыву
стали Х18Н9
6

7.

4.1 Рассеяние характеристик
прочности и нагруженности
7
Рисунок 3 - Результаты статических
испытаний образцов
хромистомолибденовой стали (Ф.
Бастенэр, М. Бастьем, Ж. Помэ)
Рисунок 4 - Эмпирическая функция
распределения пределов выносливости
стали 3Х13

8.

4.1 Рассеяние характеристик
прочности и нагруженности
8
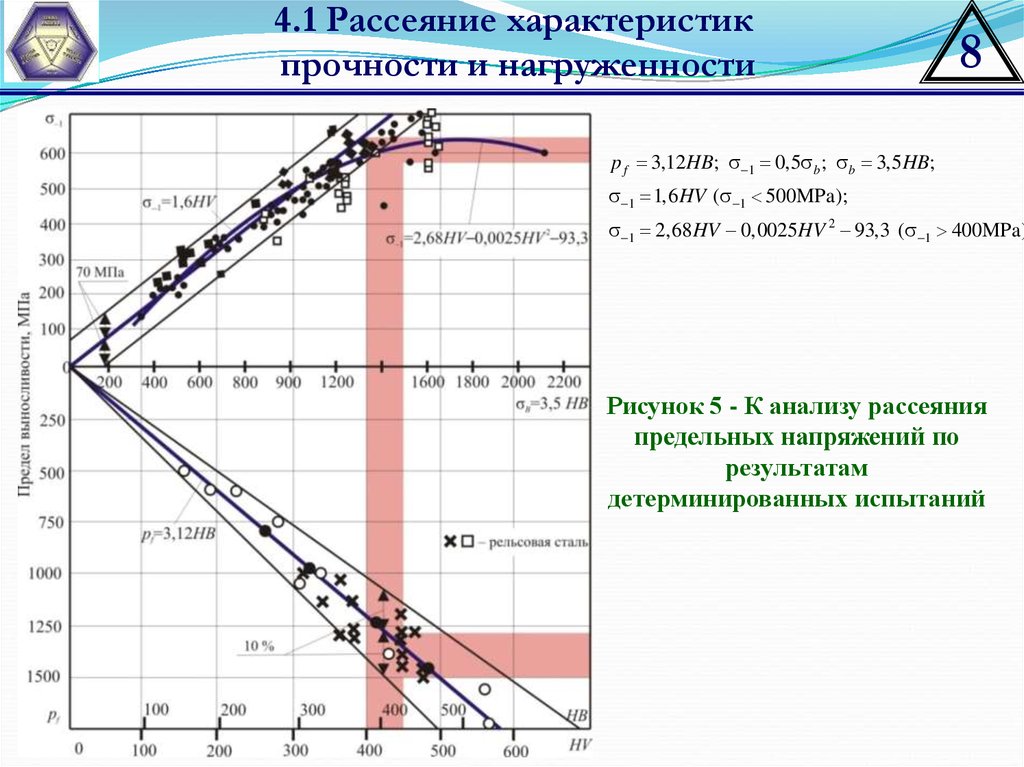
p f 3,12 HB; 1 0,5 b ; b 3,5 HB;
1 1,6 HV ( 1 500MPa);
1 2,68HV 0,0025HV 2 93,3 ( 1 400MPa)
Рисунок 5 - К анализу рассеяния
предельных напряжений по
результатам
детерминированных испытаний

9.

Модель нагрузка-прочность.
Постановка задачи
9
Условие прочности, или условие не достижения предельного состояния,
записывают так
[ ] */n,
R
(1)
R– расчетное сопротивление материала (в строительстве).
Если недопустим переход в пластическое состояние, то σ* = σy ;
при опасности хрупкого разрушения σ* = σu;
в условиях циклического нагружения σ* = σR .
Рассмотрим взаимодействие случайных процессов нагруженности
σ(t) и несущей способности σ*(t) детали или элемента сооружения с
целью
выяснения
предельного
условий
состояния
прочностной надежности.
и,
возникновения
следовательно,
недопустимого
установления
их

10.

Модель нагрузка-прочность.
Постановка задачи
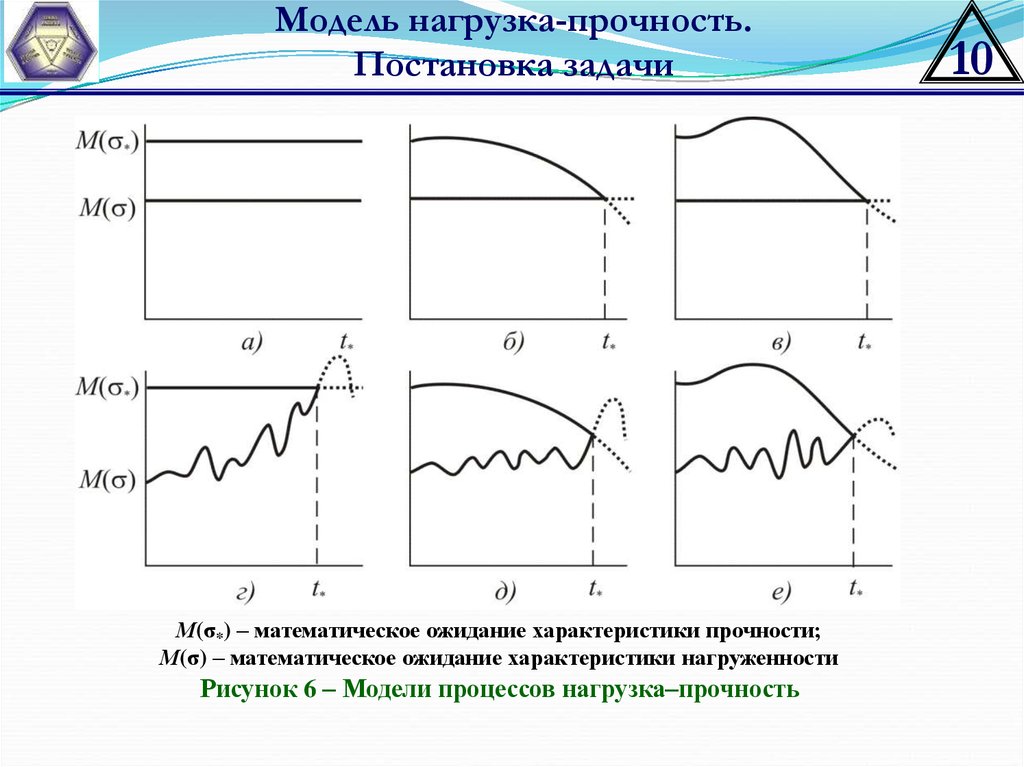
М(σ*) – математическое ожидание характеристики прочности;
М(σ) – математическое ожидание характеристики нагруженности
Рисунок 6 – Модели процессов нагрузка–прочность
10

11.

Модель нагрузка-прочность.
Постановка задачи
11
Представляется возможным
изучить взаимодействие процессов
σ(t) и σ*(t), введя функцию:
(t ) * (t ) (t ).
Рисунок 7 – Схематизация процессов нагруженности и прочности
(2)

12.

Расчет вероятности отказа
при линейном напряженном состоянии
12
f(σ) – функция распределения
характеристики нагруженности,
заменяющая стационарный
случайный процесс σ(t) на
временном интервале t1 ≤ t ≤ t2, a
f(σ*)– функция распределения
предельного напряжения,
заменяющая случайный процесс
на том же интервале времени
*min( * , * ) max ( , ). (3)
Рисунок 7 – К определению условия прочности (а) и
условия достижения предельного состояния (б)
0.
(4)

13.

Расчет вероятности отказа
при линейном напряженном состоянии
13
Когда же возникает некоторая вероятность достижения предельного
состояния или, короче, вероятность отказа, функции f(σ) и f(σ*), очевидно,
должны пересекаться, поскольку необходимо выполнить одно из условий
min ( , ) max ( , )
(5)
0
(6)
Если действующее и предельное напряжения случайны, независимы и
распределены по нормальному закону, то и их разность тоже является
случайной величиной, распределенной по тому же закону
*
(7)
S S 2* S 2
(8)
S
v
S 2* S 2
*
.
(9)

14.

Расчет вероятности отказа
при линейном напряженном состоянии
0
Q = P( Y Ј 0) =
т
- Ґ
14
2щ
й ж
ц
1
к 1 з Y- Y ч
ъ
ч
exp к- зз
ъd Y
ч
ч
SY 2p
к 2 зи SY шъ
л
ы
(10)
Нормальную функцию распределения F(Ψ)
выразим
через
нормированную
функцию
распределения Φ(z) (т.е. со средним, равным
нулю, и среднеквадратическим, равным единице)
Введем новую переменную
z
S
d
dz
S
При Ψ = 0
z
0
*
;
S
S 2* S 2
(11)
z

15.

Расчет вероятности отказа
при линейном напряженном состоянии
-
Q (Y) =
1
2p
15
s*- s
ж
зз
z
exp()dz = F зз2
зз
и
Q(Y) = F (- z )
Ss2* + Ss2
т
- Ґ
ж
зз
Q = F зззз
и
ц
s* - s ч
ч
ч
ч
2
2 ч
ч
Ss * + Ss ш
2
(12)
(13)
ц
ч
1
ч
ч
)
ч= F (2
2 ч
vY
Ss * + Ss ч
ш
s* - s
(14)
Это формула удобна для численных расчетов . Для аналитических
исследований она наоборот не удобна и ее лучше аппроксимировать степенной
1
зависимостью
жk ч
цg
з
(15)
Q = зз 2 ч
ч
ч
зиzQ ч
ш
Q
10–6–10–3
10–3–10–1
10–1–3·10–1
3·10–1–4,8·10–1
k
2,83
0,466
0,027
0,35·10–8
где квантиль
g
0,175
0,567
1,97
18,69
zQ =
s* - s
Ss2* + Ss2
1
g
1
йk (S + S ) щ
ъ = (kv 2 ) g
Q = кк
Y
2 ъ
(
s
s
)
кл *
ъ
ы
2
s*
2
s
(16)
(17)

16.

Расчет вероятности отказа
при линейном напряженном состоянии
16
Зная вероятность отказа Q, вероятность безотказной работы P детали или
элемента сооружения или, короче, их надежность, определяют как разность
между единицей и Q, т. е.
P 1 Q.
(18)
Условие прочности по вероятности отказа, аналогичное таковому по
напряжениям, запишем следующим образом
Q Q .
(19)
[Q] – нормированная вероятность отказа, обоснование которой обычно
дается технико-экономическим расчетом.
Условие (19) имеет ясный физический смысл. Так, если Q ≤ [Q] =4·10–3, то
это означает: из 1000 готовых изделий за расчетный период эксплуатации
только в четырех из них допускается наступление предельного состояния.
Введем два представления коэффициента запаса прочности, а именно:
«средний» и «экстремальный» коэффициент запаса прочности
n , (20)
nэкст
min ( , )
max ( , )
.
(21)

17.

Взаимосвязь между коэффициентами запаса
прочности и вероятностью отказа
17
Условием прочности по коэффициенту запаса будет
n n .
(22)
nэкст nэкст .
(23)
Связь между квантилем нормального распределения и коэффициентом
запаса, соответствующего определенной вероятности разрушения, получим
из формулы (16)
zF
1 nQ
S 2
2
v 2
1 nQ
v 2 nQ2
v 2
.
(24)
nQ2 (1 zQ2 v 2 ) 2nQ (1 zQ2 v 2 ) 0.
nQ
1 1 (1 zQ2 v 2 )(1 zQ2 v 2 )
1
zQ2 v 2
.
(25)

18.

Взаимосвязь между коэффициентами запаса
прочности и вероятностью отказа
k 2
k 2
1 1 1 g v 1 g v
Q
Q
nQ
.
k
1 g v 2
Q
1
k ( v 2 nQ2 v 2 ) g
.
Q
2
( nQ 1)
18
(25а)
(26)
КРИТИЧЕСКОЕ ЗНАЧЕНИЕ КОЭФФИЦИЕНТА ЗАПАСА
nк -
критический коэффициент запаса прочности, который разделяет область
возможных значений на две подобласти: если n nк , то n n , если n nк , то n nQ .
Условия недостижения и достижения предельного состояния запишем в виде
min t ( , )S max t ( , )S
(27)
min t ( , )S max t ( , )S
(28)
t ( , ),
t ( , ) –
соответственно нижний и верхний толерантные
коэффициенты, определенные с заданной доверительной вероятностью γ и уровнем
значимости α.

19.

Взаимосвязь между коэффициентами запаса
прочности и вероятностью отказа
19
Из формул (27) и (28) следует, что
1 t ( , )v
n
nQ
1 t ( , )v
1 t ( , )v
nк
1 t ( , )v
nк
nQ
(29)
(30)
(31)
nэкст
2
z
5
z
10
t ( , ) z1 1
12n0
2
n
0
(32)

20.

Расчет вероятности отказа
при произвольном законе распределения
20
Условие достижения предельного состояния
(q1 , q2 , q3 , ..., qn ) (q1 , q2 , q3 , ..., qr ) (qr 1 , qr 2 , qr 3 , ..., qn ) 0. (33)
Вероятность достижения предельного состояния
Q
( q1 , q2 , q3 , ... , qn ) 0.
... f ( q1 , q2 , q3 ,..., qn )dq1 , dq2 ,..., dqn . (34)

21.

Расчеты на надежность
при сложном напряженном состоянии
21
В случае детерминированного подхода расчет несущей способности при
трехосном напряженном состоянии (ТНС), которое характеризуется главными
напряжениями σ1 ≥ σ2 ≥ σ3, ведут по следующей схеме:
1
2
3
Теория
прочности
( 1 , 2 , 3 , mi ) ýêâ
[ ]
R
(35)
При вероятностном подходе считают известными три функции
распределения f(σi) главных напряжений σi(i = 1, 2, 3). Кроме того, описание
предельного состояния конструкции с учетом анизотропии свойств материала
производят при помощи трех функций распределения f(σ*i) предельных
напряжений в направлениях i = 1, 2, 3 действия главных напряжений.
Частные условия отказа по главным направлениям
i (q1 , q2 , q3 , ..., qn ) i (q1 , q2 , q3 , ..., qr ) i (qr 1 , qr 2 , qr 3 , ..., qn ) 0. (36)
Произведя замену переменных q1 h( i , q2 , q3 , ..., qn ), получим частные
плотности вероятностей
f ( i ) ... f [h( i , q2 , q3 , ..., qn )q2 , q3 , ..., qn ]
h( i , q2 , q3 , ..., qn )
dq2 , dq3 , ..., dqn
i
(37)

22.

Расчеты на надежность
при сложном напряженном состоянии
22
Частные вероятности Q(Аi) отказа от независимого действия случайных
главных напряжений σi по направлениям i = 1, 2, 3
0
Q( Ai ) P( i 0)
f ( i )d i .
(38)
Исходя из того общего предположения, что событие А достижения
предельного состояния при ТНС произойдет, если оно реализуется хотя бы от
одного из главных напряжений, получим, используя алгебру событий, оценку
вероятности Qс отказа детали при произвольном ТНС по частным
вероятностям отказа Q(Аi) при соответствующих ЛНС.
Qс а0 [Q( A1 ) Q( A2 ) Q( A3 ) Q( A1 )Q( A2 ) Q( A2 )Q( A3 )
3
Q( A3 )Q( A1 ) Q( A1 )Q( A2 )Q( A3 ) a0 1 1 Q( Ai ) .
i 1
0
3
Qс a0 1 1 f ( i )d i .
i 1
(39)
(39а)

23.

Расчеты на надежность
при сложном напряженном состоянии
23
Если принять гипотезу о взаимозависимости событий Ai достижения
предельного состояния, то формула (39), согласно алгебре событий, связанных
с данным испытанием, была бы записана через условные вероятности:
Qс Q( A1 ) Q( A2 ) Q( A3 ) Q( A1 A2 ) Q( A2 A3 ) Q( A3 A1 ) Q( A1 A2 A3 )
Q( A1 ) Q( A2 ) Q( A3 ) Q( A1 )Q( A2 / A1 ) Q( A2 )Q( A3 / A2 )
Q( A3 )Q( A1 / A3 ) Q( A1 )Q( A2 / A1 )Q( A3 / A1 A2 ).
(39б)
Теперь расчет на прочность можно выполнить либо по вероятности отказа
Qс [Q],
(40)
либо по соответствующему ей коэффициенту запаса прочности
экв
f ( 1 )
f ( 1 )
f ( 2 )
f ( 2 )
f ( 3 )
f ( 3 )
Q( A1 )
Алгебра
событий,
Q( A2 ) связанных с
данным
испытанием
Q( A3 )
i
[ Q ].
nQс
(41)
(i )
f [Q(A1 ), Q(A2 ), Q(A3 )] Qэкв
Qс [ F ]
i)
i)
(экв
(экв
i
[ Q ].
nQс

24.

Расчеты на надежность
при сложном напряженном состоянии
Рисунок 8 - Сравнение опасности усталостного
разрушения при различных напряженных состояниях
24

25.

Основы дифференциации
расчетов на надежность
25
Все многообразие деталей машин и элементов сооружений, подлежащих расчету на
прочность, разобьем в зависимости от экономической ответственности на четыре
группы.
Детали и элементы сооружений группы I – это объекты, несущая способность
которых лимитируется жесткостью или устойчивостью; для них достаточен
поверочный расчет на прочность либо по одному из нормированных коэффициентов
запаса прочности, либо по допускаемому напряжению (расчетному сопротивлению
материала в строительстве).
К группе II относятся силовые детали массовых машин и несущие элементы массовых
сооружений. Такие катали подлежат вероятностному расчету на прочность, что
требует, как показано выше, знания по меньшей мере параметров функций
распределения р(σ*) и р(σ) характеристик прочности σ* и нагруженности σ.
К группе III отнесем крупногабаритные силовые детали и элементы уникальных
машин и сооружений. Для таких объектов, ввиду крайне ограниченного их числа,
нет смысла искать функцию распределения предельных напряжений – следует
устанавливать их индивидуальную прочность σ*инд, которую разумно считать
детермированной величиной. Все формулы, относящиеся к объектам этой группы,
получают как частные случаи формул, приведенных для объектов II группы при
условии, что среднеквадратическое отклонение равно 0.
К IV группе отнесем силовые детали машин и элементы сооружений, для которых
действующее напряжение σ можно считать, с разумным приближением,
детермированной величиной.