Similar presentations:
Задачі на побудову перерізів
1.
Задачі на побудовуперерізів
2.
Аксіома. Якщо дві площини мають спільнуточку, то вони перетинаються по прямій, якій
належить ця точка
а
3.
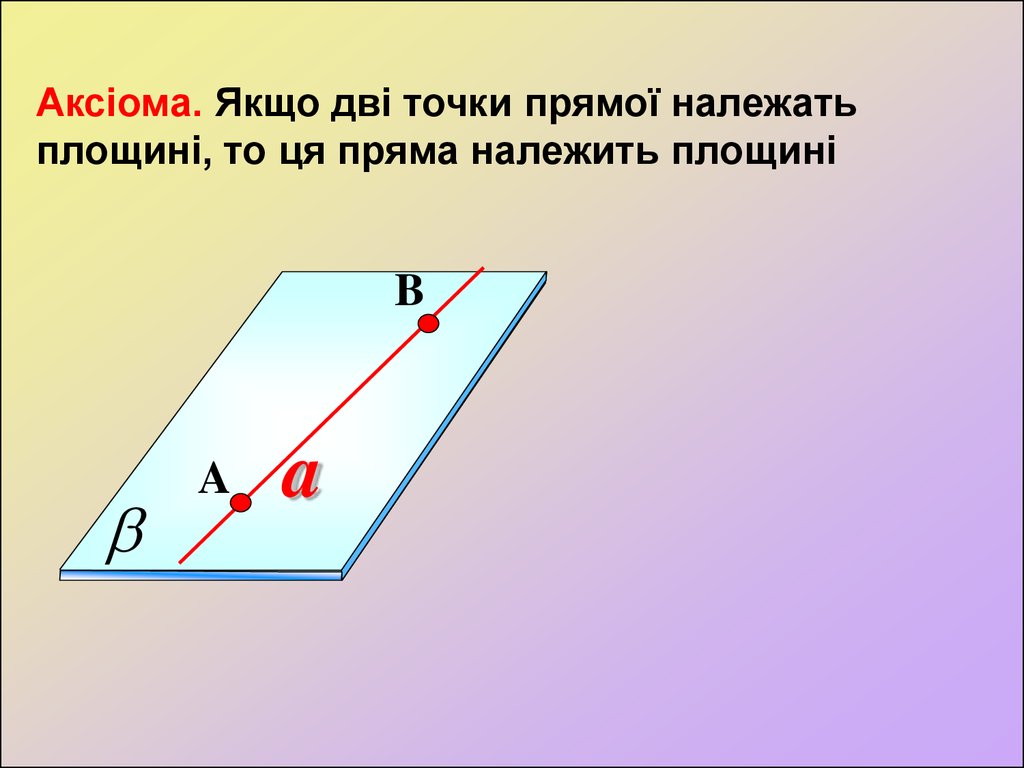
Аксіома. Якщо дві точки прямої належатьплощині, то ця пряма належить площині
B
A
a
4.
аа
5.
D1С1
K
А1
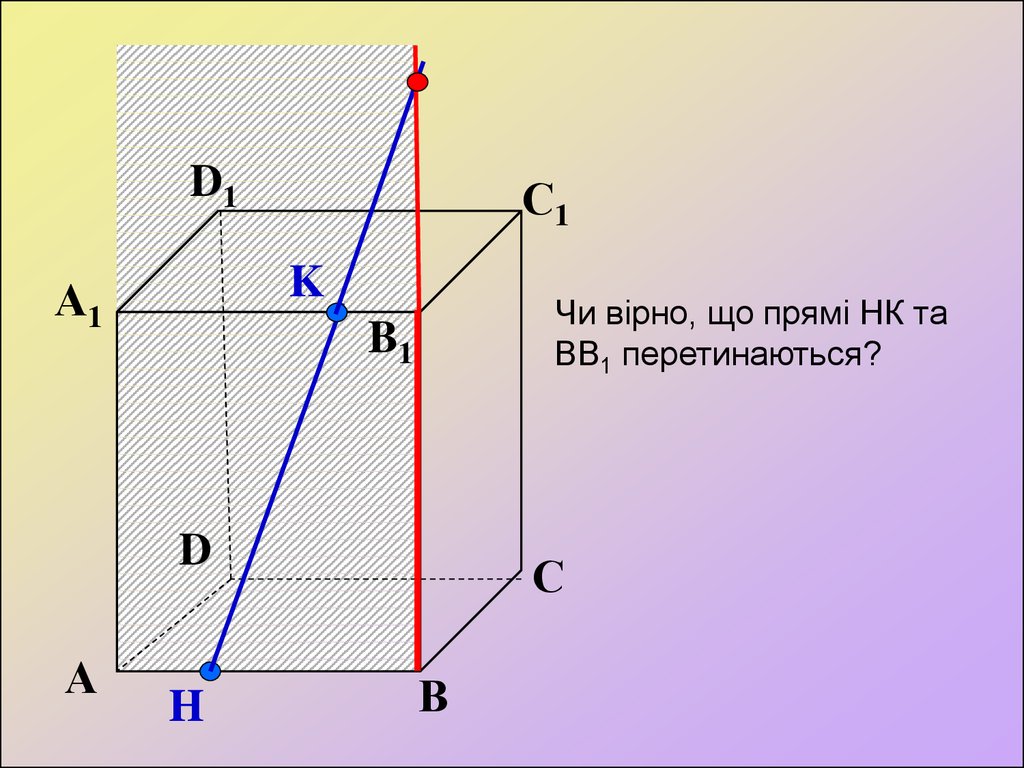
Чи вірно, що прямі НК та
ВВ1 перетинаються?
B1
D
А
H
С
В
6.
Чи вірно, що прямі НR та NKперетинаються?
D1
С1
Н
А1
R
B1
С
D
На рисунку є ще
помилка!
N
А
К
В
7.
D1С1
К
А1
B1
перетинаються?
Н
D
А
Чи вірно, що прямі
НК та ВВ1
С
N
В
8.
D1А1
К
А
С1
М
B1
Н
D
В
Чи вірно, що прямі НК та
МР перетинаються?
Р
С
N
На рисунку є ще
помилка!
9.
DЧи вірно, що
МО та АС
перетинаються?
М
О
С
А
В
10. Визначення перерізу
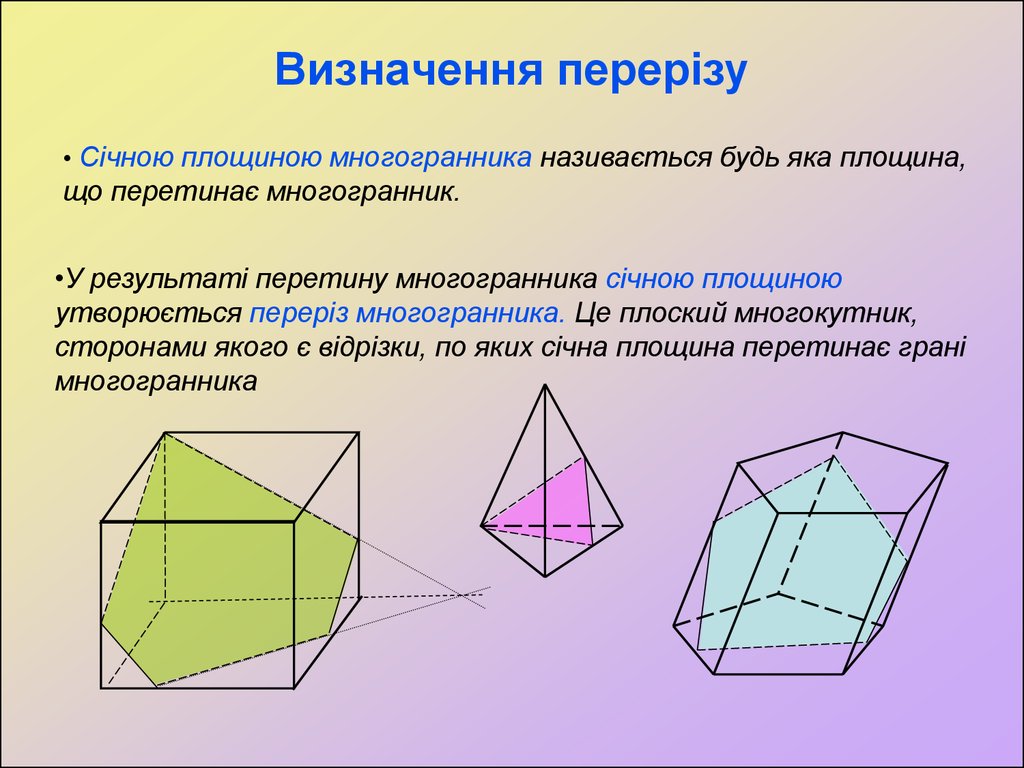
• Січною площиною многогранника називається будь яка площина,що перетинає многогранник.
•У результаті перетину многогранника січною площиною
утворюється переріз многогранника. Це плоский многокутник,
сторонами якого є відрізки, по яких січна площина перетинає грані
многогранника
11.
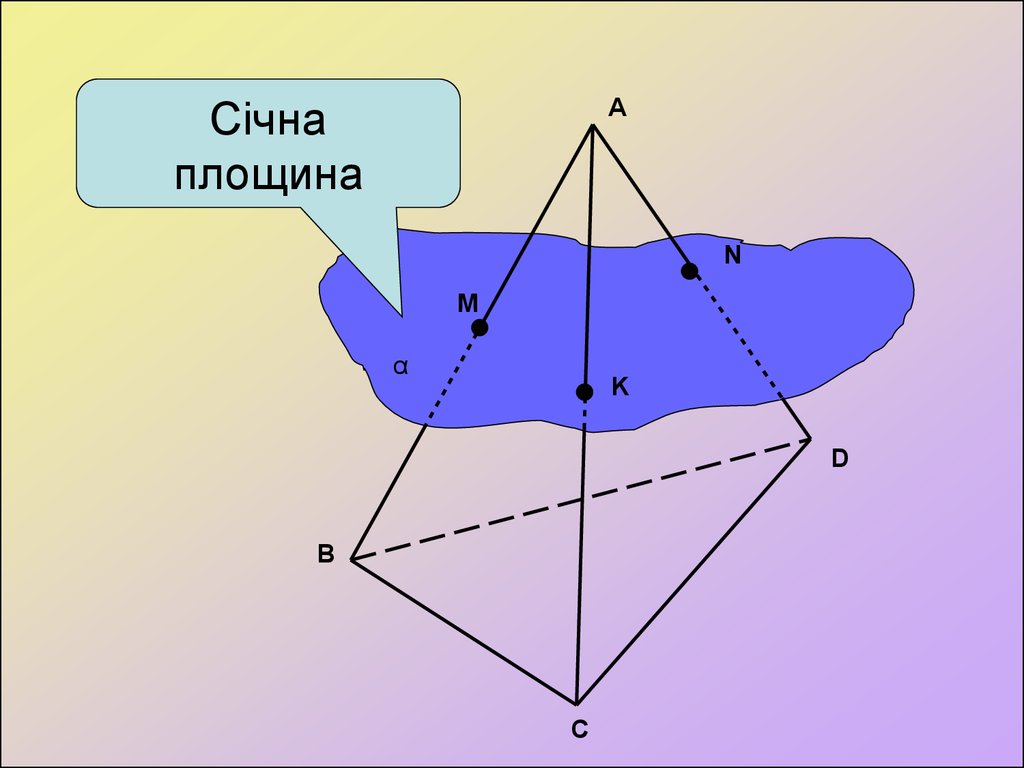
АСічна
площина
N
M
α
K
D
В
С
12.
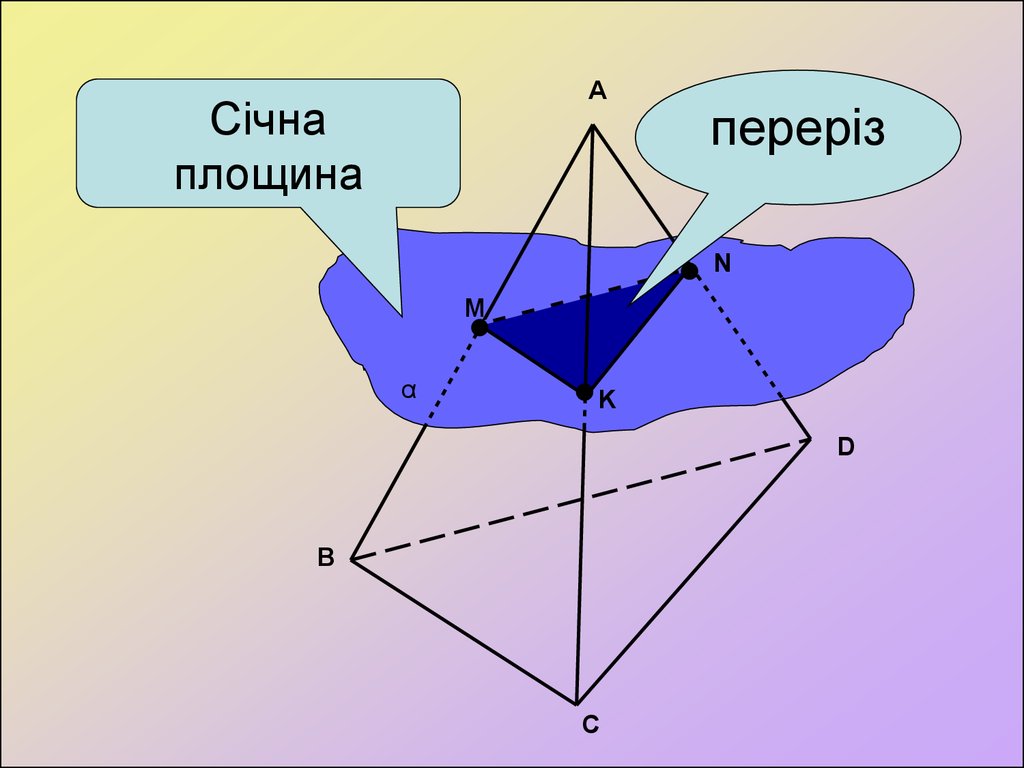
AСічна
площина
переріз
N
M
α
K
D
B
C
13.
Щоб побудувати перерізмногогранника січною площиною,
треба побудувати відрізки перетину
цієї площини з гранями многогранника
й отримати плоский многокутник.
Оскільки дві площини не можуть
перетинатися більше ніж по одній
прямій, то в грані многогранника не
може бути більше одного відрізка
перетину із січною площиною.
14.
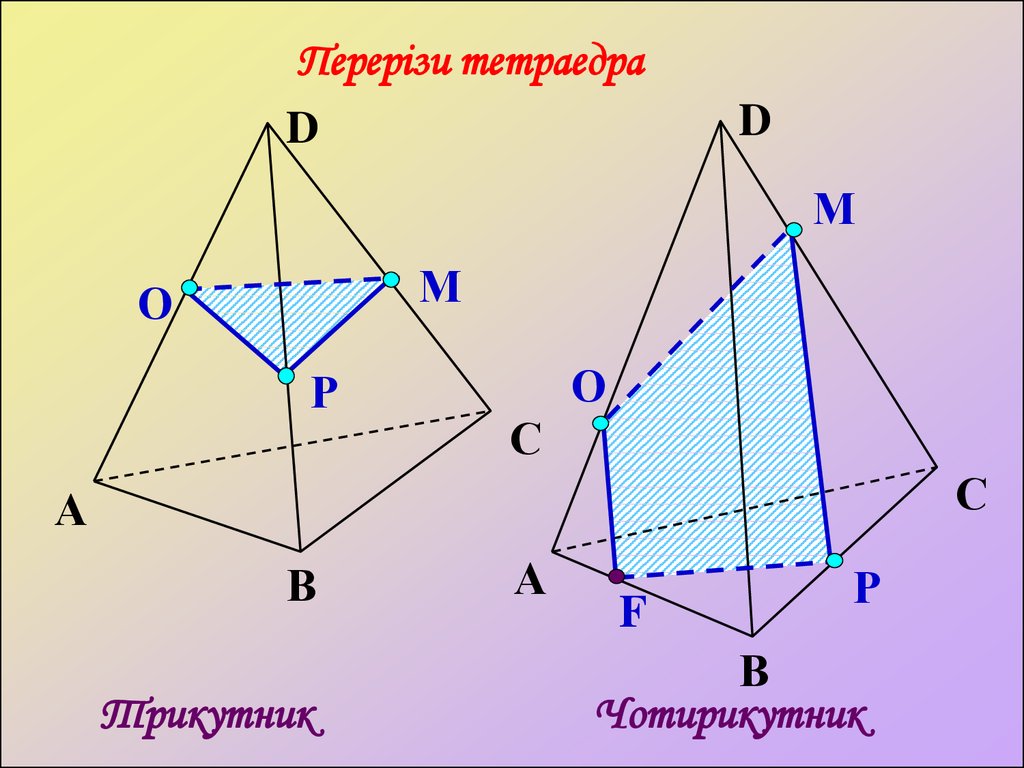
Перерізи тетраедраD
D
М
М
О
Р
О
С
С
А
В
Трикутник
А
F
Р
В
Чотирикутник
15.
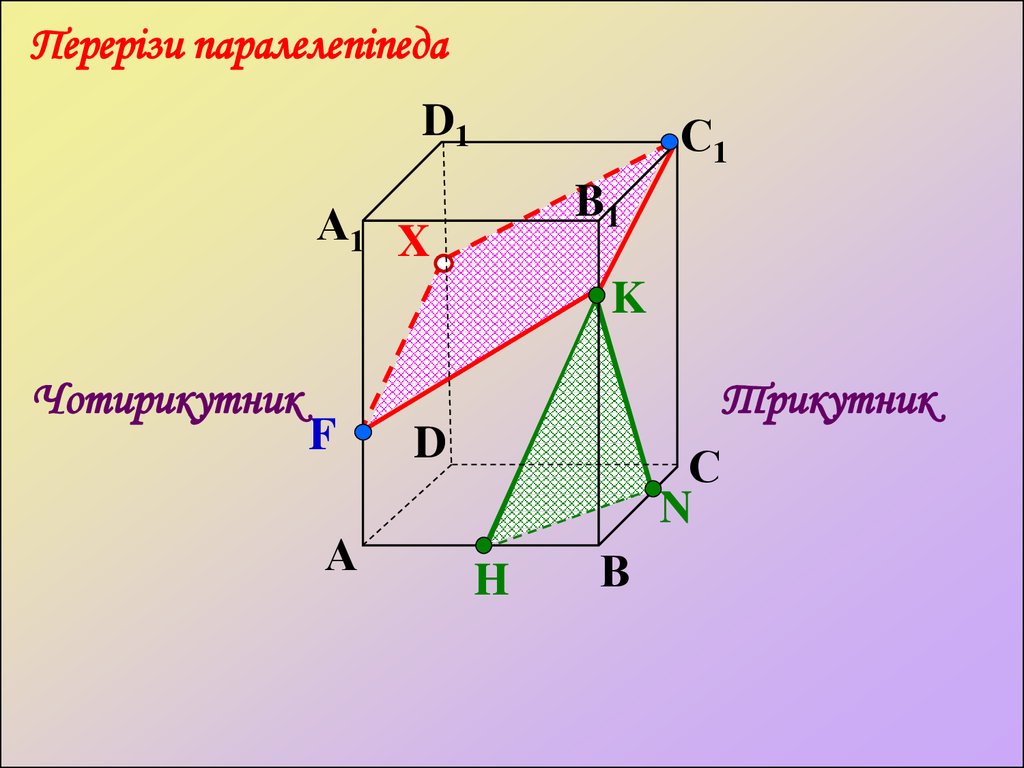
Перерізи паралелепіпедаD1
С1
B1
А1 X
K
Чотирикутник
F
А
Трикутник
D
С
N
H
В
16.
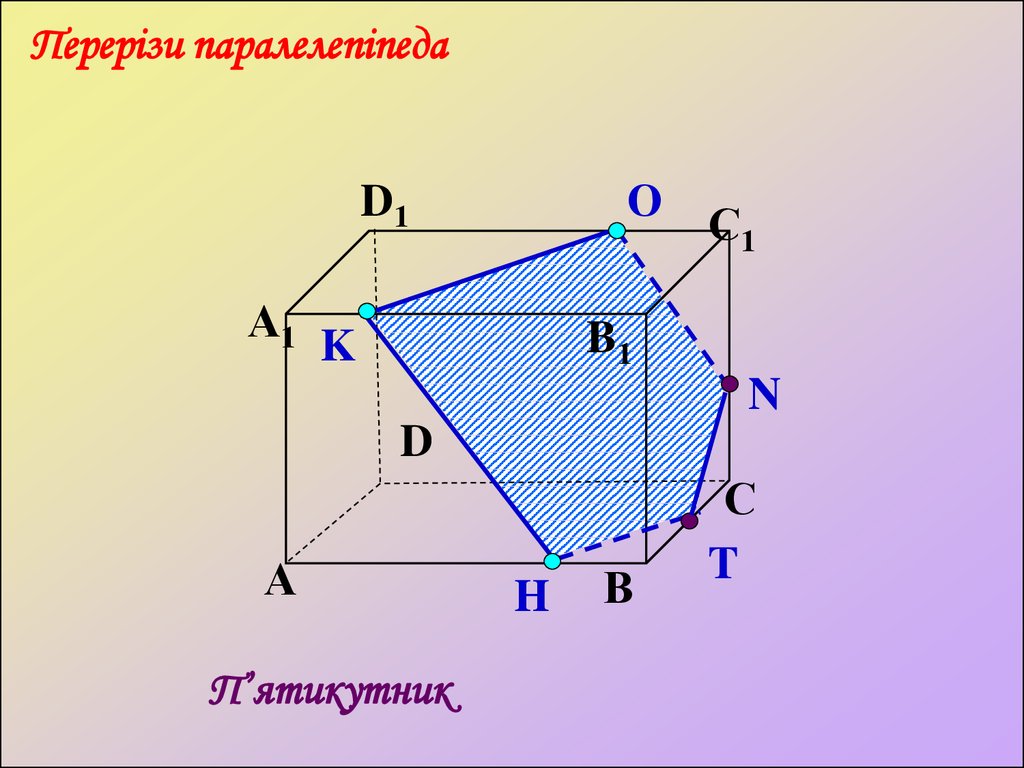
Перерізи паралелепіпедаО
D1
А1
С1
B1
K
N
D
А
П’ятикутник
H
В
С
T
17.
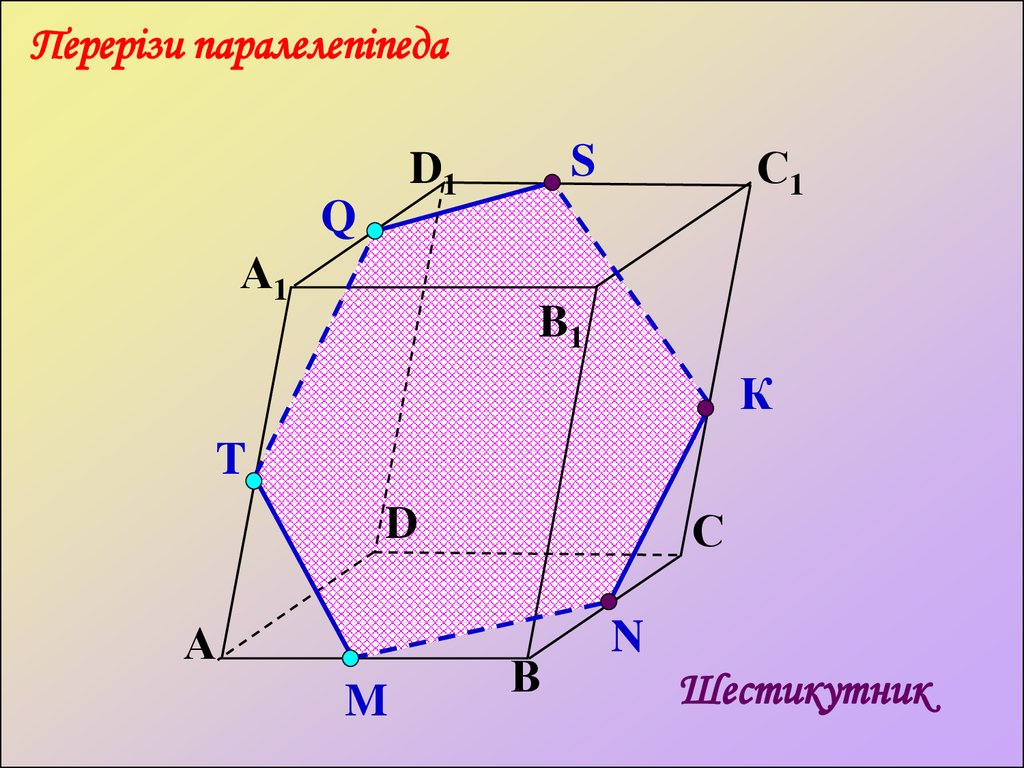
Перерізи паралелепіпедаQ
А1
С1
S
D1
B1
К
T
С
D
А
M
В
N
Шестикутник
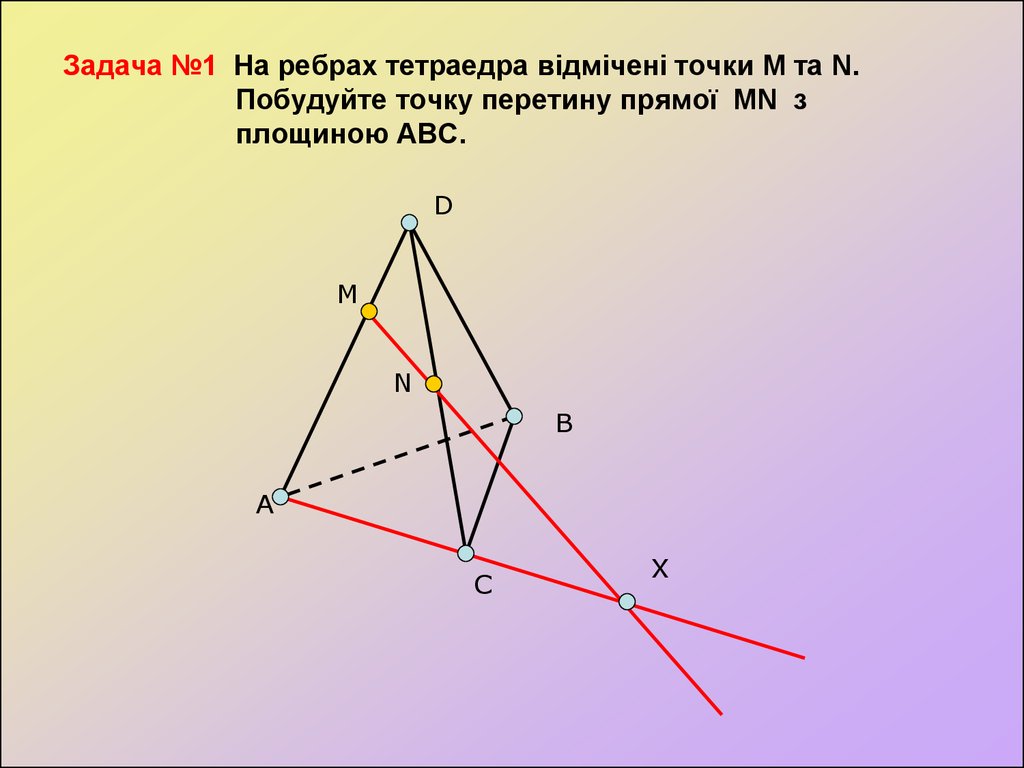
18. Задача №1 На ребрах тетраедра відмічені точки M та N. Побудуйте точку перетину прямої MN з площиною ABC.
DM
N
B
A
C
X
19.
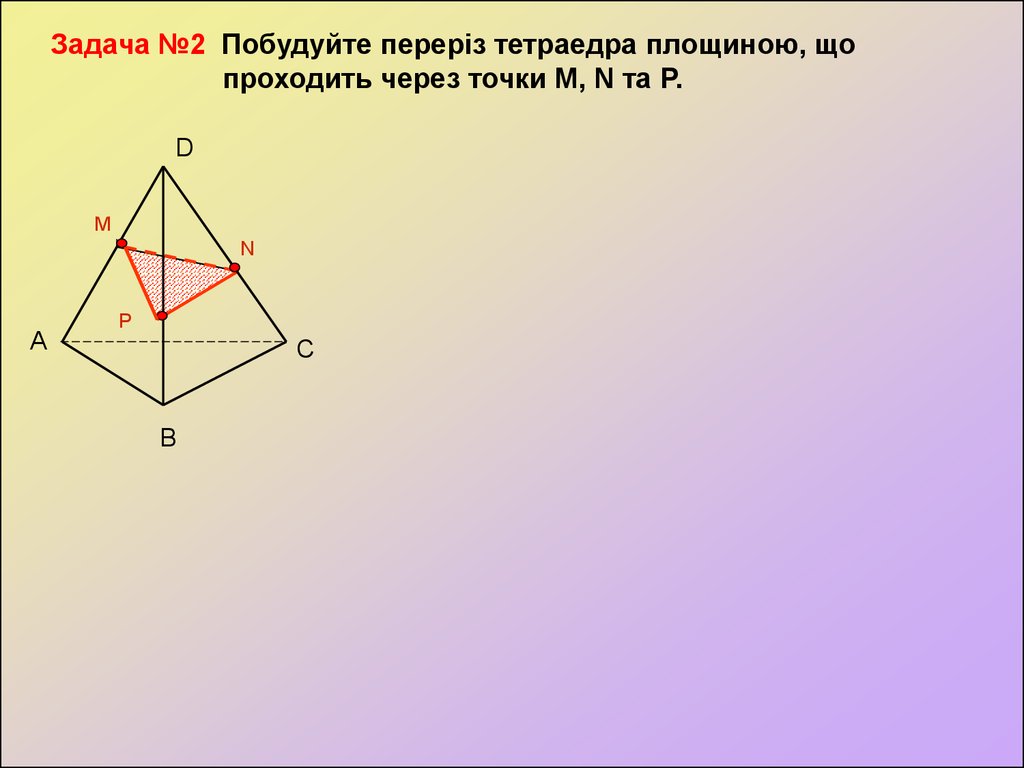
Задача №2 Побудуйте переріз тетраедра площиною, щопроходить через точки M, N та P.
D
M
N
А
P
С
В
20.
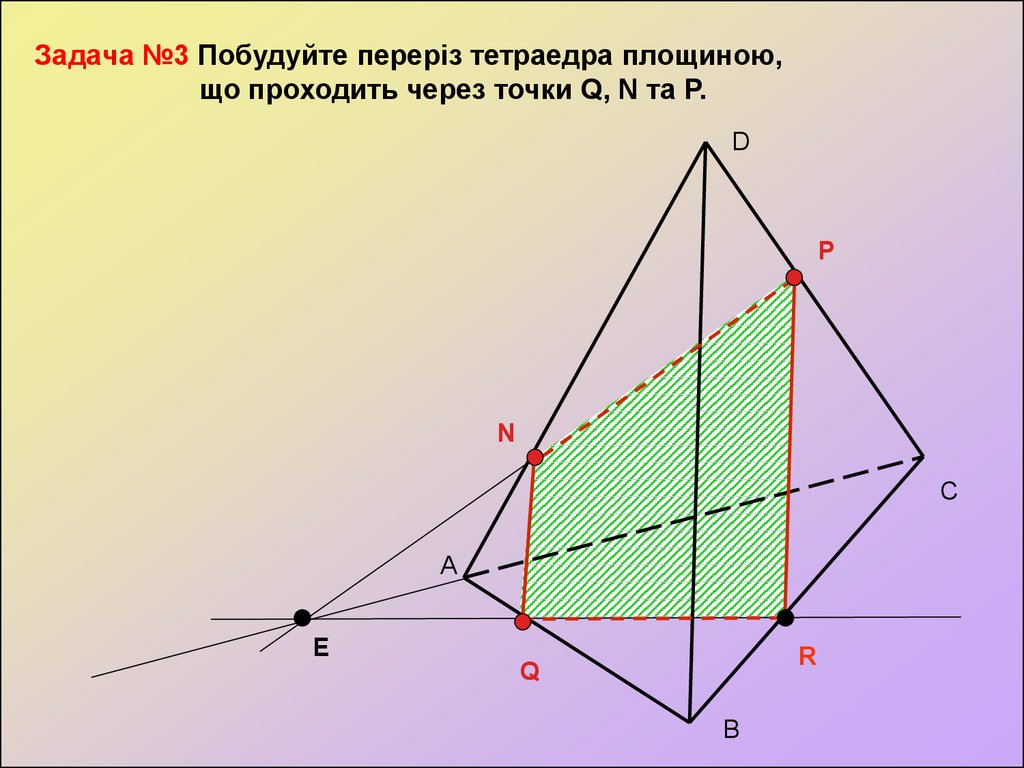
Задача №3 Побудуйте переріз тетраедра площиною,що проходить через точки Q, N та P.
D
P
N
С
А
E
R
Q
В
21.
Задача №4. Побудуйте переріз паралелепіпеда площиною HNК.D1
С1
B1
А1
K
D
А
С
N
H
В
22.
Задача №5 Побудуйте переріз паралелепіпеда площиною HNК.D1
С1
K
А1
О
B1
D
А
H
С
N
В
23.
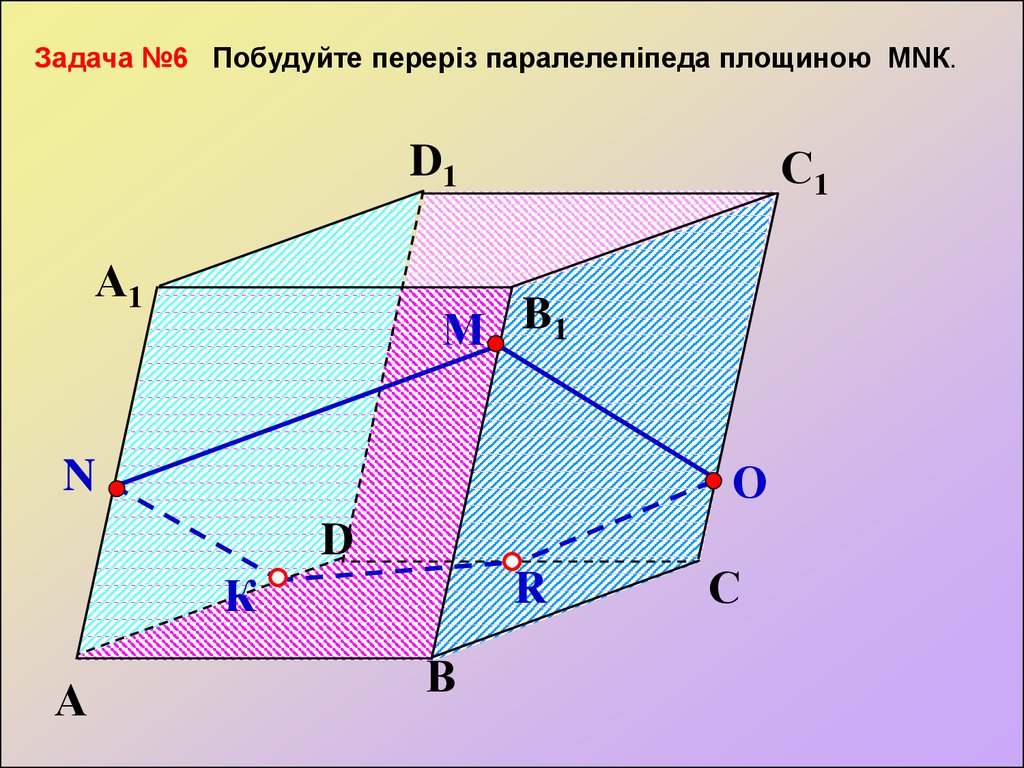
Задача №6 Побудуйте переріз паралелепіпеда площиною МNК.С1
D1
А1
М B1
О
N
D
К
А
R
В
С









 mathematics
mathematics