Критерий решений Сэвиджа. Упущенная выгода

1.

2.

Критерий Сэвиджа — один из критериев принятия
решений в условиях неопределённости. Условиями
неопределённости считается ситуация, когда
последствия принимаемых решений неизвестны, и
можно лишь приблизительно их оценить. Для
принятия
решения
используются
различные
критерии, задача которых — найти наилучшее
решение, максимизирующее возможную прибыль и
минимизирующее возможный убыток.

3.

Критерий
Сэвиджа
(критерий
MINIMAX ), в отличие от критерия
MAXIMIN, ориентирован не столько
на минимизацию потерь, сколько на
минимизацию сожалений по поводу
упущенной прибыли. Он допускает
разумный риск ради получения
дополнительной
прибыли.
Пользоваться этим критерием для
выбора стратегии поведения в
ситуации неопределенности можно
лишь тогда, когда есть уверенность в
том, что случайный убыток не
приведет фирму (инвестиционный
проект) к полному краху.

4.

Риск упущенной выгоды —
это
риск
наступления
косвенного
(побочного)
финансового
ущерба
(неполученная прибыль) в
результате неосуществления
какого-либо
мероприятия
(например,
страхования,
инвестирования и т. п.).

5.

Критерий Севиджа рассчитывается по
формуле:
min maxK =mini [ maxj (maxiXij —Xij )],
где mini maxj — поиск максимума
перебором соответственно столбцов и
строк.

6.

Расчёт минимакса состоит их четырёх этапов:
*Находится
лучший результат каждой графы в отдельности, то
есть максимум Xij (реакции рынка).
*Определяется
отклонение от лучшего результата каждой
отдельной графы, то есть maxi Xij – Xij. Полученные результаты
образуют матрицу отклонений (сожалений), так как её элементы –
это недополученная прибыль от неудачно принятых решений,
допущенных из-за ошибочной оценки возможности реакции
рынка.
*Для каждой строчки сожалений находим максимальное значение.
*Выбираем решение, при котором максимальное сожаление будет
меньше других.

7.

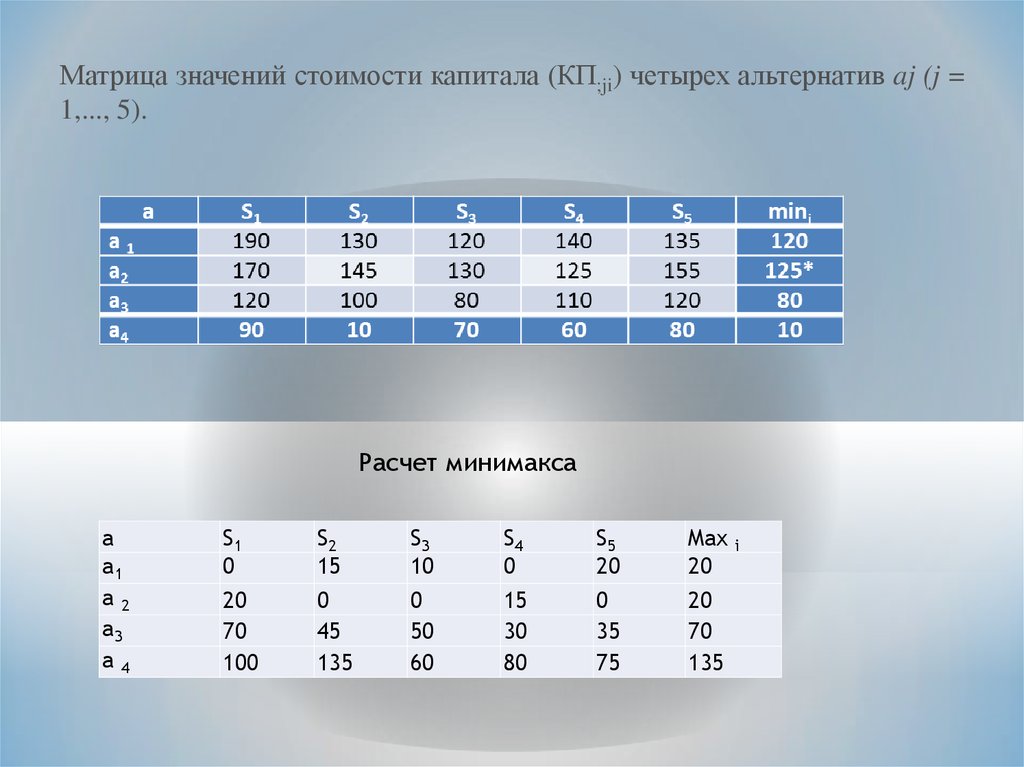
Матрица значений стоимости капитала (КП;ji) четырех альтернатив aj (j =
1,..., 5).
Расчет минимакса
а
a1
a2
a3
a4
S1
0
20
70
100
S2
15
0
45
135
S3
10
0
50
60
S4
0
15
30
80
S5
20
0
35
75
Max
20
20
70
135
i

8.

Предположим, что владелец небольшой кондитерской в начале каждого
дня закупает для реализации пирожные, спрос за день данного продукта
может быть равен 1,2,3,4 штуки. Стоимость приобретения каждого
пирожного - 50 руб., а цена реализации 60 руб. за единицу. Продать
невостребованные пирожные на следующий день невозможно, поэтому
остаток всегда распродается в конце дня по цене 30 руб. Владельцу
кондитерской нужно принять решение и определить, сколько пирожных
должно быть закуплено в начале каждого дня.
В нашем примере, покупатели определяют спрос, поэтому возможный
исход представляет собой "фактор неопределенности". Чтобы определить
вероятность каждого исхода, составим список возможных решений и
соответствующих им исходов.

9.

Предполагаем, что количество закупаемых пирожных равняется 1, тогда сумма возможного
дохода составит: 1*60-1*50=10 руб. Следовательно, в первом столбце проставляется 10
независимо от возможного спроса.
Если решение о количестве закупаемых пирожных будет равно 2, то сумма возможного
дохода в этом случае составит для спроса 1 шт: 1*60 +1*30-2*50= -10 руб, для спроса 2
пирожных и более: =2*60-2*50=20 руб. Это значения для второго возможного решения и
спроса более двух пирожных.
Аналогично, рассчитывается исход события, если решение закупать составит 3 и 4 штуки
пирожных. Возможный доход также учитывается с учетом реализации в конце дня
непроданных пирожных.
После того, как отдача в денежном выражении для любой комбинации решений и исходов
определена, ответим на вопрос "сколько пирожных должен закупать владелец каждый
день", используя каждое из правил принятия решений.
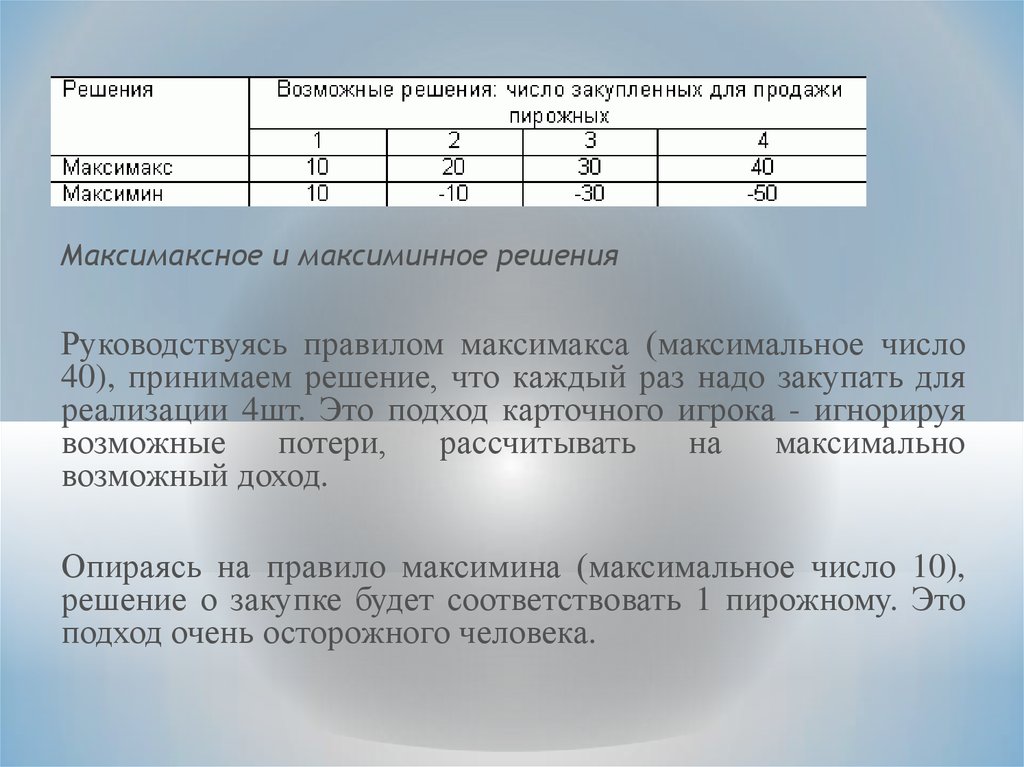
На основании полученных данных таблицы возможных доходов, выберем максимальное и
минимальное число для каждого столбца и составим таблицу.

10.

Максимаксное и максиминное решения
Руководствуясь правилом максимакса (максимальное число
40), принимаем решение, что каждый раз надо закупать для
реализации 4шт. Это подход карточного игрока - игнорируя
возможные
потери,
рассчитывать
на
максимально
возможный доход.
Опираясь на правило максимина (максимальное число 10),
решение о закупке будет соответствовать 1 пирожному. Это
подход очень осторожного человека.

11.

Необходимо отметить, что любое решение не
может
иметь
чисто
положительных
результатов, поэтому любое организационное
решение - это компромисс. И в каждом случае
руководитель должен сделать выбор между
неизбежными отрицательными моментами.