Similar presentations:
Методы машинного обучения
1. Методы машинного обучения
5. Логические методыклассификации
2. Методы классификации
Метрические методы классификации
Логические методы классификации
Линейные методы: метод стохастического градиента
Линейные методы: метод опорных векторов
Методы восстановления регрессии
Нелинейная и непараметрическая регрессия
Байесовские методы классификации
Поиск ассоциативных правил
Нейронные сети и бустинг
Прогнозирование временных рядов
Видеолекции: http://shad.yandex.ru/lectures
Презентации и текст: http://www.machinelearning.ru/wiki
Машинное обучение (курс лекций, К.В.Воронцов)
2 / 40
3. План лекции
Понятия закономерности иинформативности
• Понятие закономерности
• Интерпретируемость
• Информативность
Решающие деревья
• Алгоритм ID3
• Небрежные решающие деревья – ODT
• Бинаризация данных
3 / 40
4. Идея логических методов
Смоделировать человеческую логику принятиярешений в ситуациях, когда есть неточности,
нечеткости, прецеденты и т.п.
Ожидания: правильность и понятность людям
(что весьма полезно в определенных предметных
областях, таких как медицина, геология,
социология, техническая диагностика и т.д.).
Идея получить не только решающее правило,
но и понять, разумно ли оно, а также выявить
какие логические закономерности оно
сформировало на основе имеющихся данных.
4 / 40
5. Логическая закономерность (определение и свойства)
p–positive
n–
negative
непротиворечивая
(чистая)
закономерность,
которую нужно
построить для
каждого класса
предсказательная
сила (способность)
противоречивая
закономерность
(бесполезна,
не несет никакой
информации о
классах)
5 / 40
6. Логическая закономерность (требования и задачи)
Отдельная закономерность – это еще не классификатор, это«недоклассификатор». Каждый из таких «недоклассификаторов»
не может решить задачу, но если набрать их достаточное
количество и построить композицию, то она – сможет.
n должно быть как можно меньше, p – как можно больше.
Эти требования могут входить в противоречия, поэтому
необходимо найти разумный компромисс.
Решаемые задачи:
• Определить, что есть закономерность (на основе статистических критериев).
• Какой вид могут иметь правила (чаще это конъюнкции простых условий).
• Научиться их строить (это, как правило, переборные алгоритмы).
• Понять, как объединять правила в композиции (существует много разных
идей – независимо, последовательно и т.д.).
6 / 40
7. Пример реализации свойства интерпретируемости
такие правиласоответствуют
способу
мышления
врача или
кредитного
аналитика
естественное накладывание
пороговых условий для
количественных признаков
отнесение к классу указано с некоторой «уверенностью» (риски
отрицательного исхода и дефолта); вероятность уверенности
находится из обучающей выборки (доля отрицательных исходов)
7 / 40
8. Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]
большой /маленький
дано: обучающая выборка из
6 объектов одного класса (слева) и
6 объектов другого класса (справа);
задача: установить, какое правило
породило эти объекты
дополнительно: рассматриваются
чистые закономерности, которые
выделяют все объекты одного
класса и не выделяют другого
8 / 40
9. Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]
треугольники /четырехугольники
9 / 40
10. Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]
длина выпуклой оболочки фигурысущественно больше, чем ширина /
выпуклая оболочка фигуры имеет
одинаковую длину и ширину
10 / 40
11. Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]
спирали противчасовой стрелки /
спирали по часовой стрелке
идея была в том, чтобы научить компьютер «видеть такие закономерности»,
т.е. не только сканировать рисунок, но и вычислять информативные признаки;
при том, что количество информации для их выделения весьма велико,
что наглядно демонстрирует этот тест (нужно не только понять, что это
спираль и установить, в какую сторону она закручена)
11 / 40
12. Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]
больше черных фигур /больше белых фигур
12 / 40
13. Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]
на разных выпуклостях /на одной выпуклости
видно, насколько разные признаки должен уметь извлекать компьютер
из картинки, чтобы уметь решать все эти задачи, при том, что человек
с ними справляется достаточно легко
13 / 40
14. Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]
наличие осевой симметрии /отсутствие осевой симметрии
14 / 40
15. Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]
точка на центральной ветке /точка не на центральной
ветке
можно придумать и более хитрые задачи (фотографии мужчин/женщин, марки
машин, виды животных и растений, картины в подлиннике и в копии и т.д.)
НУЖНО УМЕТЬ ВЫДЕЛЯТЬ ВАЖНЫЕ ПРИЗНАКИ
15 / 40
16. Что нужно делать, чтобы извлекать закономерности из данных?
в учебныхзадачах
признаки даны
пространство
поиска зависит
от задачи
определяем, что
является критерием
поиска (свертка двух
критериев)
эвристики для
сокращения полного
перебора, который
лучше, но долгий
признак – это тоже функция от объекта, поэтому закономерность может являться признаком
16 / 40
17. В каком виде ищут закономерности? (часто используемые виды)
число признаков jдолжно быть маленьким,
чтобы закономерность
поняли люди
задачи
дифференциальной
диагностики
(должны подтвердиться
хотя бы несколько
симптомов)
пороговое условие
может быть также
односторонним
симптом – это
признак, синдром –
их совокупность
для заболевания
17 / 40
18. В каком виде ищут закономерности? (часто используемые виды)
снова используетсянебольшое число
признаков j (некое
подпространство)
если вокруг точки x0 описали шар
радиусом w0, в котором много
объектов одного класса (а других –
мало), то это закономерность
получаем линейную
комбинацию признаков
(будут рассмотрены далее),
а не , но здесь
складываются «км с кг»
метрика r, аналог того, что
было в метрических методах
(эталонность сравнения)
способ
вычисления оценки
способ
вычисления оценки
используется прецедентная
логика в проверке и
интерпретации результата
18 / 40
19. Часто используемые критерии информативности
для определения лучшейбезошибочность
точность
все предложенные
здесь меры не
очень адекватны,
т.к. для них
легко найти
контрпримеры
(см. след. слайд)
линейная функция стоимости
относительная точность
19 / 40
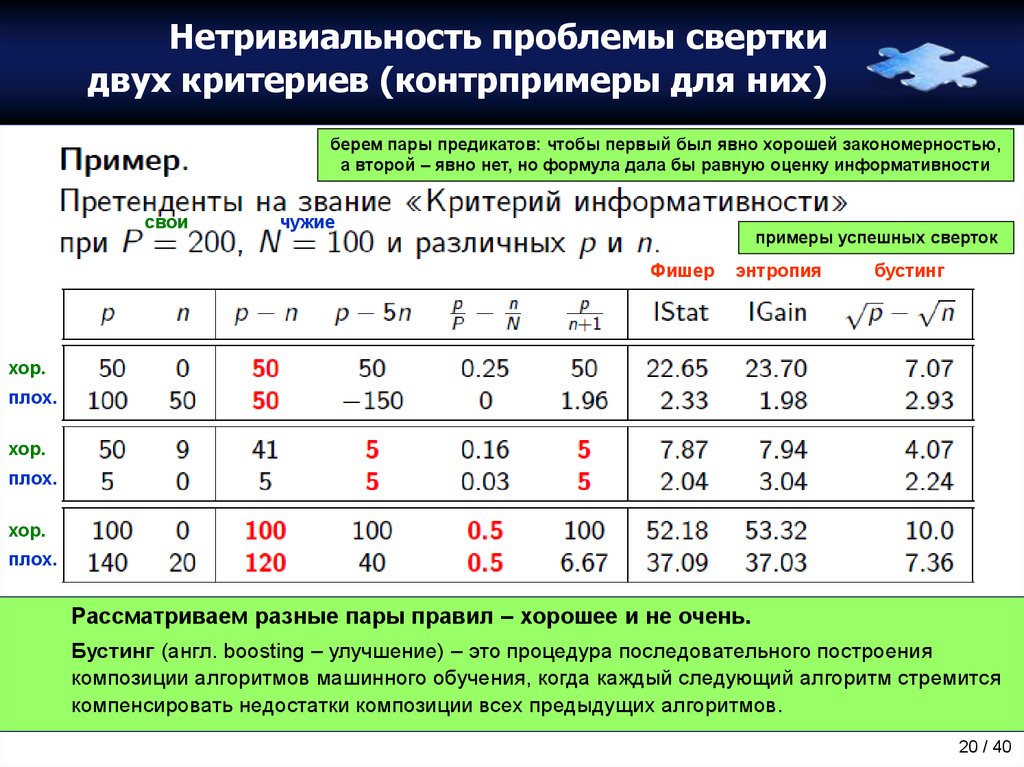
20. Нетривиальность проблемы свертки двух критериев (контрпримеры для них)
берем пары предикатов: чтобы первый был явно хорошей закономерностью,а второй – явно нет, но формула дала бы равную оценку информативности
свои
чужие
примеры успешных сверток
Фишер
энтропия
бустинг
хор.
плох.
хор.
плох.
хор.
плох.
Рассматриваем разные пары правил – хорошее и не очень.
Бустинг (англ. boosting – улучшение) – это процедура последовательного построения
композиции алгоритмов машинного обучения, когда каждый следующий алгоритм стремится
компенсировать недостатки композиции всех предыдущих алгоритмов.
20 / 40
21. Часто используемые критерии информативности (обзор)
нет однозначногоответа на то, КАКОЙ
критерий лучше и
КАК сворачивать
два критерия p и n,
но есть с десяток
разумных способов
это сделать
21 / 40
22. Часто используемые критерии информативности (IGain)
частотаэнтропия
всей выборки
энтропия
части выборки
частота
энтропия
части выборки
Информационная энтропия – мера неопределенности или непредсказуемости информации,
неопределенность появления какого-либо символа алфавита.
Если есть два взаимоисключающие исхода, которым приписаны вероятности (которые в сумме
дают 1), то мы можем связать с этими исходами количество информации, которое они несут.
«Чем меньше вероятность исхода, тем больше информации мы получаем, если этот исход
реализуется». Энтропия определяется как мат.ожидание количества информации.
Первое событие берем с вероятностью q, второе (1-q) и получаем формулу (см. выше).
Вычисляем энтропию, которой обладает обучающая выборка, ДО того, как узнали предикат R,
и ПОСЛЕ того. Разность этих энтропий покажет, сколько информации R несет о делении
выборки на классы. Разность энтропий называется информационным выигрышем.
22 / 40
23. Часто используемые критерии информативности (IStat)
выделяетпредикат R
– log
используется для того,
чтобы получить
величину, которая
чем больше, тем лучше
чтобы предикат R был
закономерностью, должен
быть перекос в сторону p
Другая идеология того, как получить оценку информативности – это статистические тесты.
Пусть предикат R, покрывающий долю объектов выборки, и класс с, также покрывающий долю
объектов, (если трактовать их как вероятностные события) – это независимые события.
Пусть предикат R зафиксирован, а у классов есть вероятность CPN+P вариантов
распределиться по выборке, и мы считаем все эти варианты равновероятными. Т.е. это другой
способ сказать, что предикат и класс – это независимые случайные величины.
Интуиция говорит, что чтобы R был закономерностью, n/p должно быть много меньше N/P,
а статистика выдает точную количественную формулу (см. выше), которая позволяет судить
о том, насколько не случайно это событие (соответствующее соотношение n и p).
23 / 40
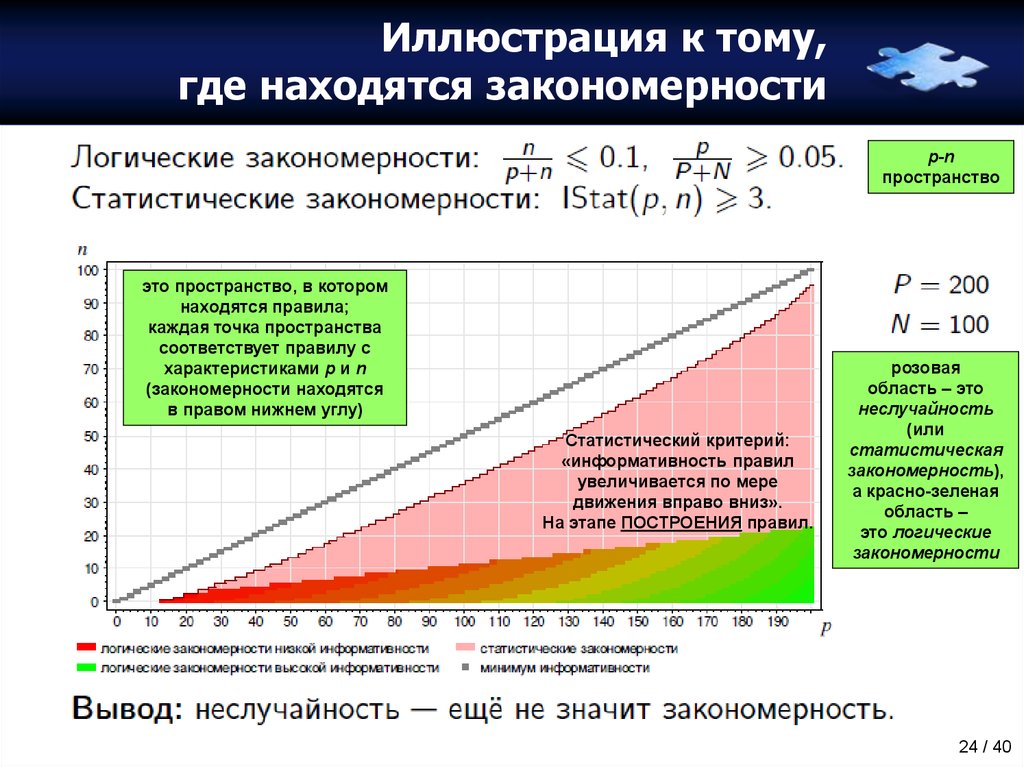
24. Иллюстрация к тому, где находятся закономерности
p-nпространство
это пространство, в котором
находятся правила;
каждая точка пространства
соответствует правилу с
характеристиками p и n
(закономерности находятся
в правом нижнем углу)
Статистический критерий:
«информативность правил
увеличивается по мере
движения вправо вниз».
На этапе ПОСТРОЕНИЯ правил.
розовая
область – это
неслучайность
(или
статистическая
закономерность),
а красно-зеленая
область –
это логические
закономерности
24 / 40
25. Парето-критерий информативности в (p, n)-плоскости
примертого, как
можно
отбирать
закономерности
недоминируемые
– это те,
над
которыми
нет
доминанта
вид закономерностей
не важен
( , шары
и т.п.)
нашли недоминируемые
закономерности (лучше
них нет), сохранили их,
затем удалили их с
картинки и «обнажили»
второй слой, из которого
также выбираются
недоминируемые и т.д.;
далее из отобранного
конструируем
классификатор
25 / 40
26. Как происходит поиск информативных закономерностей?
алгоритмов множество,здесь представлена
общая идея, под которую
подходят следующие
частные случаи
общая эвристика,
которая может быть
реализована по-разному
одно или несколько
по любому критерию
по идее, количество правил не должно
увеличиваться – оставляем некоторое
изначально заданное их количество
26 / 40
27. Определение бинарного решающего дерева
у каждогообъекта есть
только одна
возможность
дойти до листа
предикат
метка
класса
27 / 40
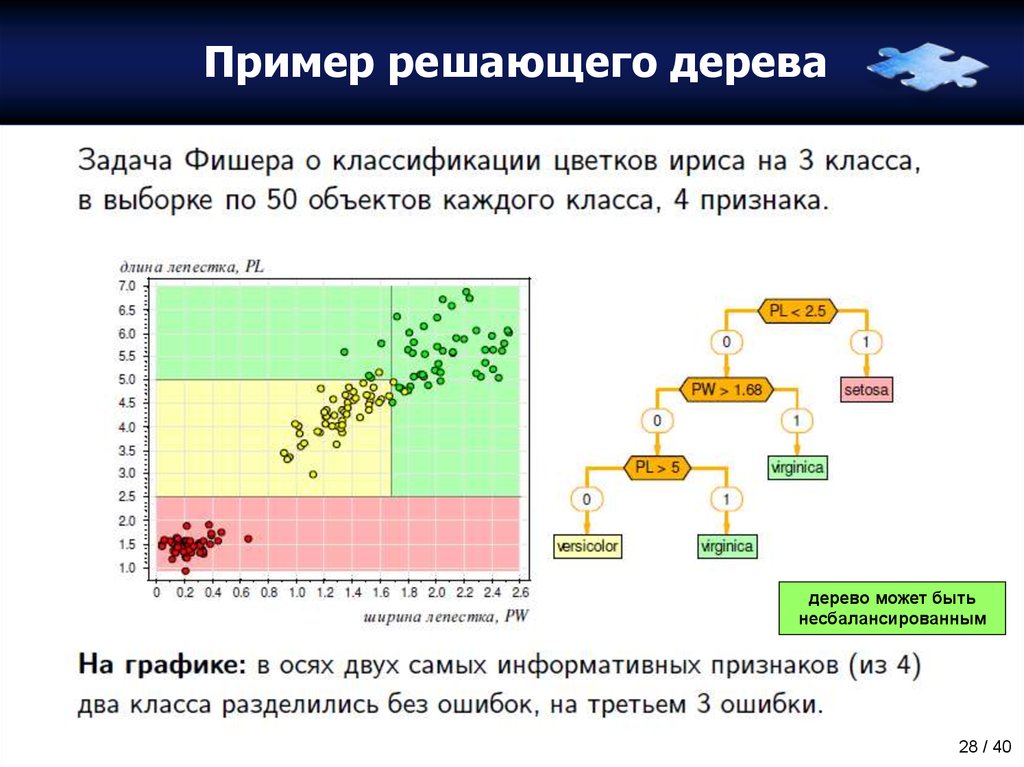
28. Пример решающего дерева
дерево может бытьнесбалансированным
28 / 40
29. Решающее дерево, покрывающее набор конъюнкций
деревопокрывает все
пространство
и разворачивается в
список
конъюнкций,
поэтому
решающие
деревья
относят к
логическим
методам
условие
попадание
объекта в
терминальную
вершину (лист)
можно записать
как конъюнкцию
условий вершин,
через которые
он прошел
(некоторые –
с отрицаниями)
29 / 40
30. Жадный алгоритм построения дерева ID3
в начале передаетсявся выборка U
Жадный алгоритм
построения дерева ID3
рекурсивная процедура, берущая на входе
часть выборки и строящая поддерево
когда нечего расщеплять, создается лист
когда есть что расщеплять, строится функционал (по критерию ветвления I),
который пытается разбить объекты так, чтобы какие-то классы желательно
целиком ушли в одно из поддеревьев (см. след. слайд)
построен неинформативный предикат (даже когда
получена просто малая мощность множества);
в этом случае листу приписывается (мажоритарный)
класс – которого было больше в выборке U
было несколько классов
30 / 40
31. Разновидности многоклассовых критериев ветвления
насколько многоинформации о разделении
выборки на классы несет ;
разность энтропии до того,
как его узнали, и после дает
выигрыш в информации
предикат тем более информативен, чем больше пар объектов,
принадлежащих одному классу, пошли в одно поддерево
двойственный критерий предикат тем более информативен, чем
больше пар объектов, принадлежащих разным классам, пошли в
разные поддеревья (разделимость ЛУЧШЕ объединения)
31 / 40
32. Обработка пропусков (логические алгоритмы толерантны к пропускам)
дерево обладает тем свойством, что можно не знать значениявсех признаков, но тем не менее успешно классифицировать
если для объекта отсутствует признак, объект исключается из оценки информативности
оценивается вероятность того, что объекты идут по одной или по другой ветке (для всех ветвей)
четко: 0 или 1
размыто: вероятность
дочерней вершины
32 / 40
33. Решающие деревья ID3: достоинства и недостатки
любой признаклюбого типа
можно
бинаризовать
иногда листы
построены
по малым
(статистически
ненадежным)
подвыборкам
33 / 40
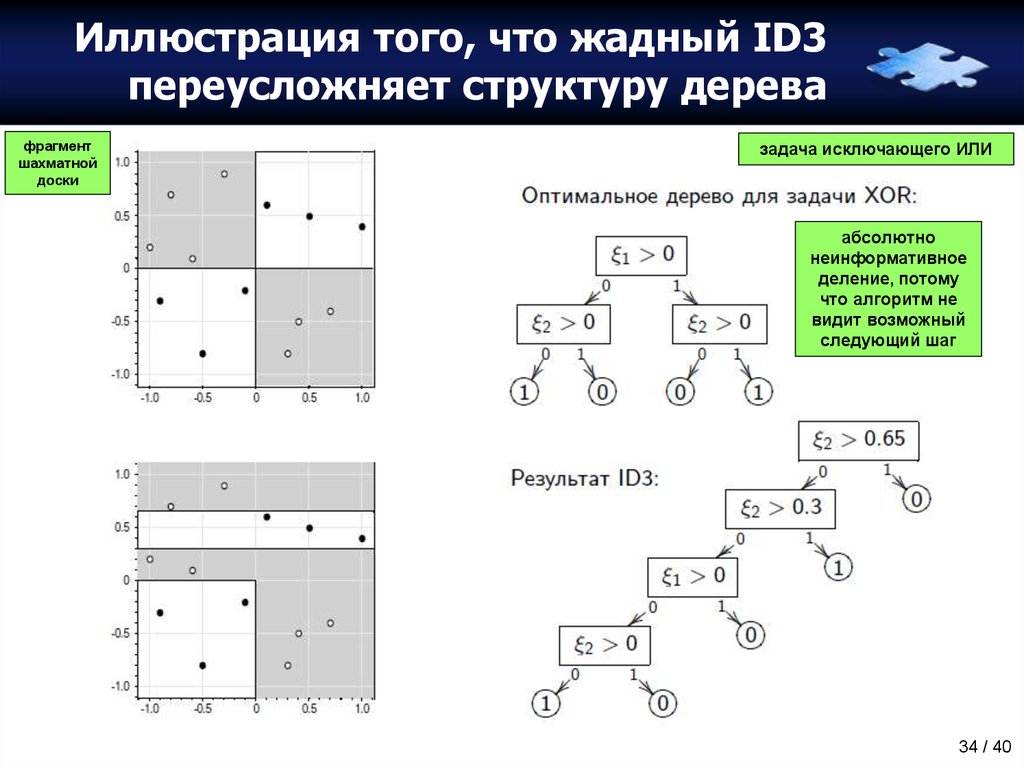
34. Иллюстрация того, что жадный ID3 переусложняет структуру дерева
фрагментшахматной
доски
задача исключающего ИЛИ
абсолютно
неинформативное
деление, потому
что алгоритм не
видит возможный
следующий шаг
34 / 40
35. Редукция дерева («стрижка кустов», pruning: С4.5, CART)
хотим понять, какиевершины оказались
лишними – до которых
не дошел ни один объект
контрольной выборки
от этой вершины удаляется поддерево и она заменяется на лист
если до этой
вершины
дошла какая-то
часть объектов,
считаем число
ошибок
вопросы при
реализации: в
каком порядке
обходить,
сверху или
снизу, случайно
или по
критериям и т.п.
срезали правое поддерево
срезали левое поддерево
срезали все
35 / 40
36. Небрежные решающие деревья – ODT (Oblivious Decision Tree)
идея строитьдеревья
быстро
на каждом уровне
используется
один признак, для
каждого признака
устанавливается
один порог
композиция таких
конструкций
используется в
Матрикснет
Яндекса
36 / 40
37. Алгоритм обучения ODT ODT (Oblivious Decision Tree)
при формальнойпостановке простой
задачи возникает
довольно
непрозрачный
алгоритм
37 / 40
38. Задача бинаризации вещественного признака
разбиение наинформативные
зоны
1. не надо ставить пороги
между объектами одного
и того же класса (это
ухудшит информативность)
2. можно объединять тройки
соседних интервалов
(крестики, нолики,
крестики) до тех пор,
пока увеличивается
информативность
(огрубляем тонкости)
38 / 40
39. Способы разбиения области значений признака на зоны
идея того, как ещеможно дробить ось
значений признака
на значения, чтобы
сократить перебор
(чтобы перебирать
не все точки)
Способы разбиения области
значений признака на зоны
предыдущий вариант
если выборка 1000, то бьем по 100
здесь в каждом разбиении может
быть разное количество объектов
хорошо работает
для больших данных
(для выборок
избыточной длины)
39 / 40







![Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967] Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]](https://cf.ppt-online.org/files/slide/x/xRNl4y3ndQ8LPaItUp5hHk7bA0wFuoDjcE6OWi/slide-7.jpg)
![Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967] Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]](https://cf.ppt-online.org/files/slide/x/xRNl4y3ndQ8LPaItUp5hHk7bA0wFuoDjcE6OWi/slide-8.jpg)
![Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967] Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]](https://cf.ppt-online.org/files/slide/x/xRNl4y3ndQ8LPaItUp5hHk7bA0wFuoDjcE6OWi/slide-9.jpg)
![Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967] Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]](https://cf.ppt-online.org/files/slide/x/xRNl4y3ndQ8LPaItUp5hHk7bA0wFuoDjcE6OWi/slide-10.jpg)
![Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967] Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]](https://cf.ppt-online.org/files/slide/x/xRNl4y3ndQ8LPaItUp5hHk7bA0wFuoDjcE6OWi/slide-11.jpg)
![Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967] Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]](https://cf.ppt-online.org/files/slide/x/xRNl4y3ndQ8LPaItUp5hHk7bA0wFuoDjcE6OWi/slide-12.jpg)
![Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967] Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]](https://cf.ppt-online.org/files/slide/x/xRNl4y3ndQ8LPaItUp5hHk7bA0wFuoDjcE6OWi/slide-13.jpg)
![Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967] Как понимают закономерность люди? Тесты М.М. Бонгарда [Проблема узнавания, 1967]](https://cf.ppt-online.org/files/slide/x/xRNl4y3ndQ8LPaItUp5hHk7bA0wFuoDjcE6OWi/slide-14.jpg)





















 informatics
informatics








