Similar presentations:
Векторы. Скалярные величины
1. Векторы
Выполнила ученица 9г классаШколы-гимназии № 5
Рузиева Саяра
2. Скалярные величины
Скалярнаявеличина (скаляр) – это
физическая величина, которая имеет
только одну характеристику – численное
значение. Примеры скалярных величин:
масса (m), путь (S), работа (А), время (t) и
т.д.
3. Векторные величины
Векторнаявеличина (вектор) – это
физическая величина, которая имеет две
характеристики – модуль и направление в
пространстве.
Примеры
векторных величин: скорость (),
сила (), ускорение () и т.д.
4.
Вектором называется направленный отрезок.а
В
А
•о
Векторы обозначаются:
АВ, а, о
Вектор о- нулевой. lol=0
Модулем вектора называется длина содержащего его отрезка.
l AB l=AB
Ненулевые векторы называются коллинеарными, если они лежат
либо на одной, либо на параллельных прямых.
5.
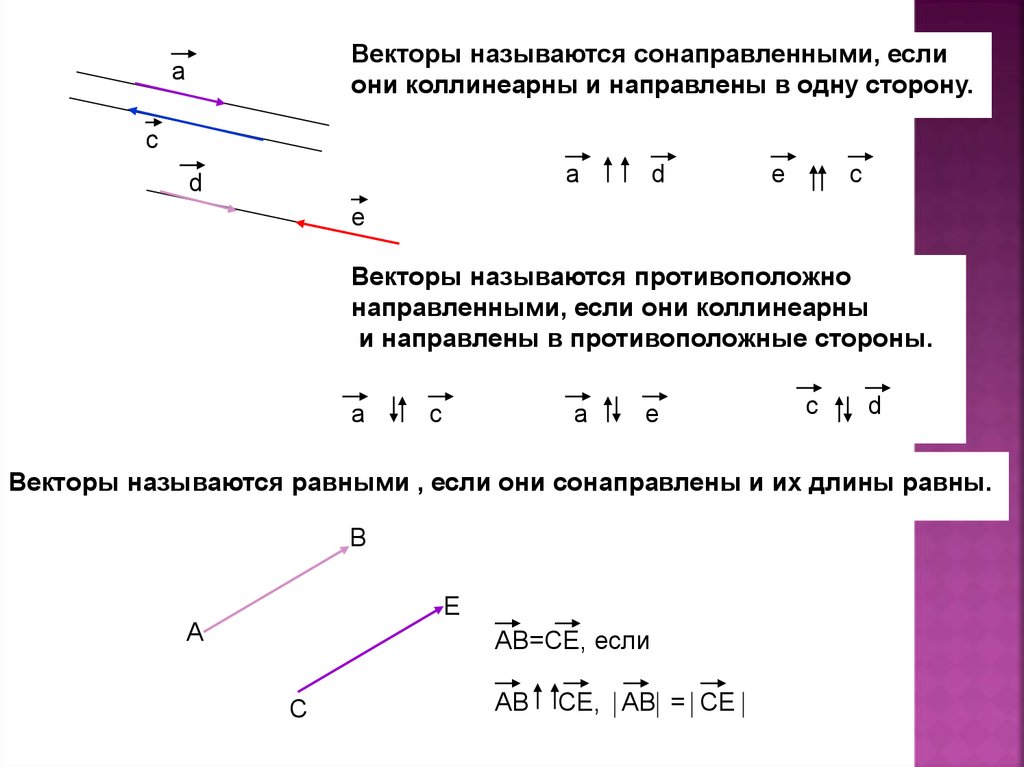
Векторы называются сонаправленными, еслиони коллинеарны и направлены в одну сторону.
а
с
a
d
d
e
c
е
Векторы называются противоположно
направленными, если они коллинеарны
и направлены в противоположные стороны.
а
с
а
е
c
d
Векторы называются равными , если они сонаправлены и их длины равны.
В
Е
А
АВ=СЕ, если
С
АВ
СЕ, АВ = СЕ
6.
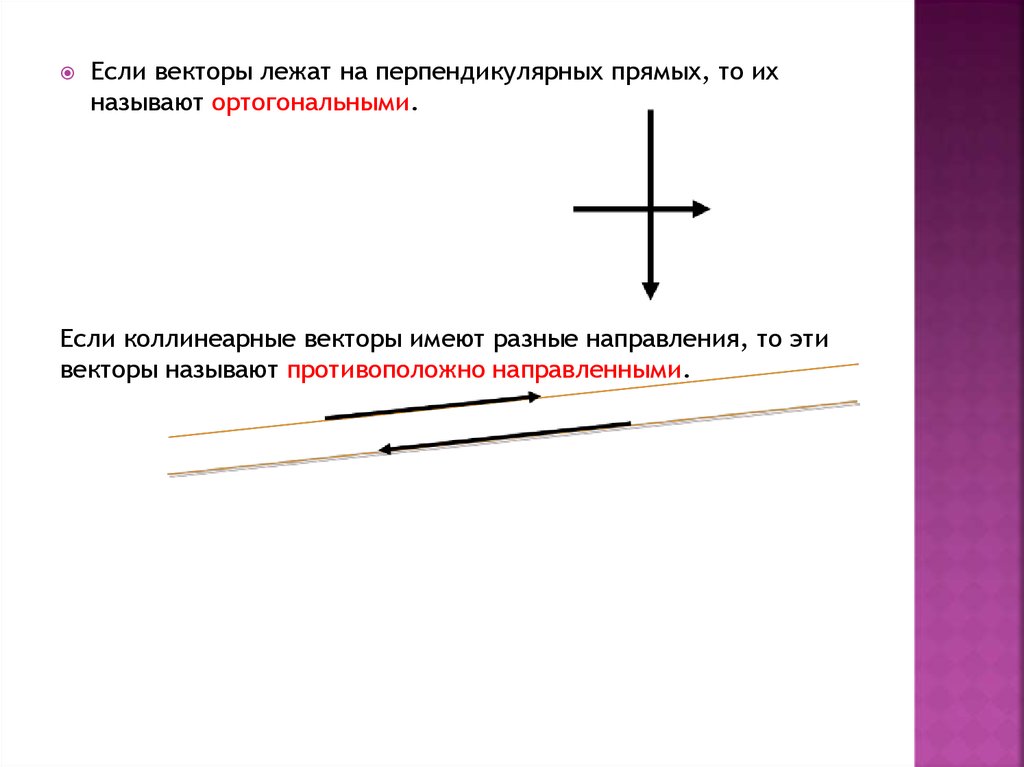
Если векторы лежат на перпендикулярных прямых, то ихназывают ортогональными.
Если коллинеарные векторы имеют разные направления, то эти
векторы называют противоположно направленными.
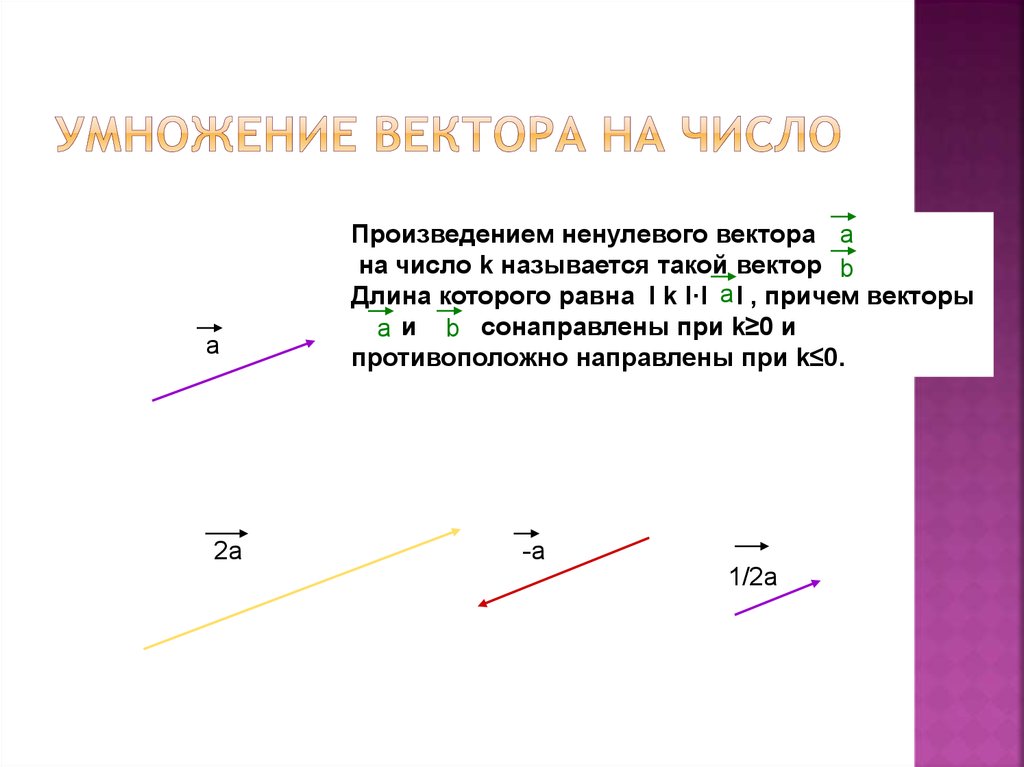
7. Равенство векторов
Векторыявляются равными, если они
сонаправлены и их модули равны.











 mathematics
mathematics








