Similar presentations:
Grafka i komunikacja człowieka z komputerem
1. Grafika i Komunikacja człowieka z komputerem
Wykład 12. Skrócony sylabus
LpTemat –wykłady
Godziny
Temat – laboratorium
1
Wstęp do grafiki komputerowej
3
Interfejs w C++, funkcje graficzne 3
2
Algorytmy rastrowe i wektorowe i
wektorowe
Przekształcenia 2D, rzutowanie i
przekształcenia 3D
3
Algorytmy rastrowe i wektorowe
3
3
Przekształcenia 2D, rzutowanie i
przekształcenia 3D
3
6
Reprezentacja obiektów graficznych
3
Przekształcenia 3D+reprezentacja
3
7
Animacja, Flash+Action Script
3
Animacja, Flash+Action Script
3
Razem
15
Razem
15
3
godziny
3. Literatura
• Literatura główna– Michał Jankowski, Elementy grafiki komputerowej, WNT.
– Foley J. D., Van Dam A., Wprowadzenie do grafiki komputerowej,
– P. Shirley, Fundamentals of Computer Graphics, sec. ed. A K Peters,
2005
• Literatura uzupełniająca
– Theo Pavlidis, Grafika i przetwarzanie obrazów, WNT.
– Jan Zabrodzki, Grafika komputerowa, metody i narzędzia, WNT.
– Paweł Zakrzewski. Adobe Flash CS6 i ActionScript 3.0. Interaktywne
projekty od podstaw. Helion 2013
– James D.Foley, Fundamentals of interactive Computers Graphics,
Reading.
– Preparata F. P., Shamos M. I., Geometria obliczeniowa. Wprowadzenie.
4. Wybrane zastosowania grafiki komputerowej:
Gry, Multimedia, TV, Filmy (w sensie produkcji),
Wojsko i przemysł (symulatory),
Wspomagane komputerowo projektowanie,
Nauka, Medycyna (symulacje, wizualizacja),
Kartografia,
przygotowanie publikacji (DTP).
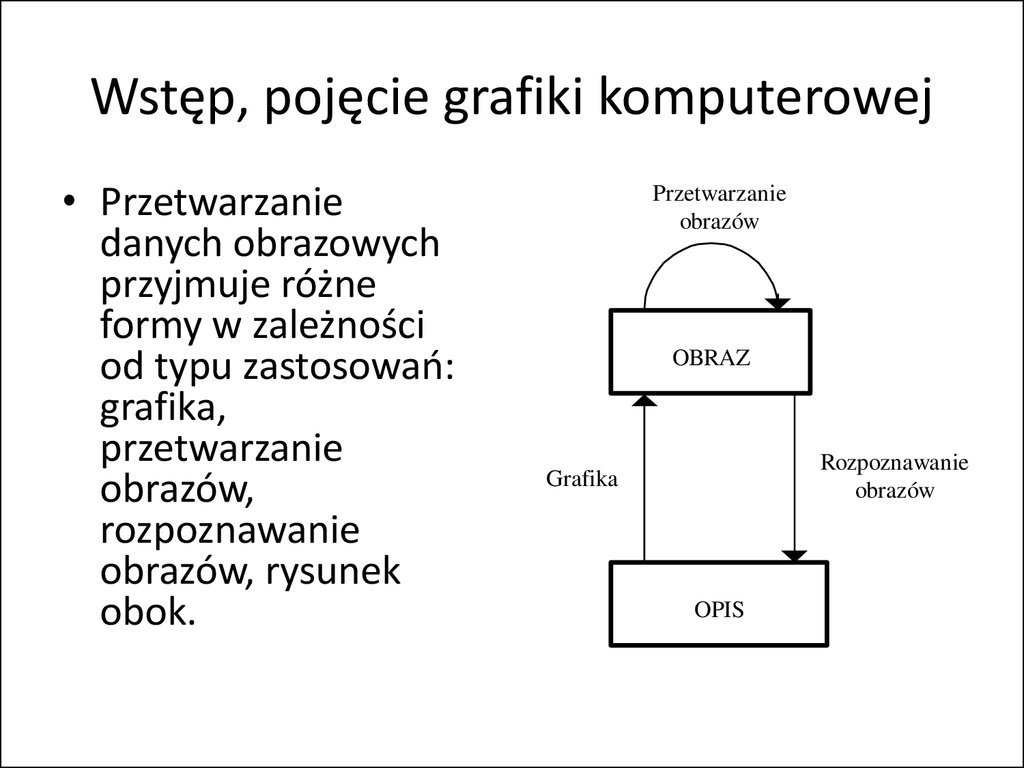
5. Wstęp, pojęcie grafiki komputerowej
• Przetwarzaniedanych obrazowych
przyjmuje różne
formy w zależności
od typu zastosowań:
grafika,
przetwarzanie
obrazów,
rozpoznawanie
obrazów, rysunek
obok.
Przetwarzanie
obrazów
OBRAZ
Rozpoznawanie
obrazów
Grafika
OPIS
6. Grafika komputerowa
• Zajmuje się tworzeniem obrazów na podstawieinformacji nieobrazowej, np. narysować odcinek
między
dwoma
punktami
o
zadanych
współrzędnych.
• Wyodrębnia się także grafikę interaktywną, która
odnosi się do urządzeń i systemów akceptujących
dane wejściowe podawane w postaci graficznej,
np. narysować odcinek między dwoma punktami
wskazanymi na ekranie.
7. Grafika komputerowa
• Przykładowymi zadaniami grafiki komputerowej są:– Narysuj odcinek łączący dwa punkty,
– Wypełnij wielokąt,
– Skonstruuj powierzchnię wypukłą (tzn. podaj punkty, które
obejmują wszystkie pozostałe punkty),
– Obróć punkt, przesuń punkt i inne przekształcenia,
– Narysuj krzywą przechodzącą przez dane punkty,
– Narysuj powierzchnię przechodzącą przez dane punkty,
– Utwórz scenę przy zadanym oświetleniu i danych
obiektach.
8. Przetwarzanie obrazów
• Dotyczy zagadnień, w których dane wejściowe iwyjściowe mają postać obrazów.
• Przykładowymi zadaniami przetwarzania obrazów
są:
– Usuwanie zakłóceń,
– Kompresja obrazu,
– Polepszenie kontrastu obrazu w celu usunięcia
prześwietlenia, niedoświetlenia lub zamazania,
– Zredukowanie obrazu kolorowego do obrazu
mającego dwa poziomy luminacji.
9. Rozpoznawanie obrazów
• Dotyczy tworzenia opisu obrazu lubzakwalifikowanie obrazu do szczególnej klasy
obrazów. Rozpoznawanie obrazów jest
zagadnieniem odwrotnym do grafiki
komputerowej.
• Przykładowymi zadaniami rozpoznawania
obrazów są:
– rozpoznawanie pisma przez automatyczny sorter
listów,
– automatyczna diagnostyka lekarska,
10. Grafika komputerowa a przetwarzanie i rozpoznawanie obrazów
• Pewne problemy występujące w ww. dziedzinachmogą być wspólne, a pewnych sytuacjach związki
między tymi dziedzinami nie są oczywiste.
• Wspólne elementy dotyczą struktur danych, ich
przechowywania, kompresji danych.
• Związki mniej oczywiste występują np. przy
znajdowaniu konturów (zadanie dla
przetwarzania obrazów) i przy wypełnianiu
konturów (zadanie dla grafiki komputerowej) związek polega na tym, że jedno zagadnienie jest
odwróceniem drugiego.
11. Przykład
• Przykładem zagadnienia, w którym istnieje integracja trzechdziedzin -przesyłanie obrazów dokumentów przez linie łączności:
– przekształcenie znaku alfanumerycznego na jego postać bitową zamiana opisu znaku na jego obraz (grafika komputerowa), np. dość
dobre efekty uzyskuje się za pomocą matrycy 300 bitowej,
– zapis obrazu mającego postać mapy bitowej za pomocą mniejszej
liczby bitów, np. obraz 20x15=300 bitów można zapisać za pomocą
mniejszej liczby bitów -znane są przekształcenia, które pozwalają
najwyżej 6-cio krotnie zmniejszyć liczbę bitów potrzebnych do
przesyłania obrazu -zadanie przetwarzania obrazu,
– odtworzenie znaku na podstawie jego obrazu -zadanie rozpoznawania
obrazu.
• Uwaga: znaki alfanumeryczne można przesyłać za pomocą mniejszej
liczby bitów (np. znak można zapisać za pomocą 8 bitów), ale
problem pozostaje przy przesyłaniu np. obrazów w tekście.
12. Formy danych obrazowych
• Dalsze slajdy dotyczą wspólnych struktur danych:– Algorytmy wykorzystywane w przetwarzaniu danych
obrazowych działają dla różnych form danych
obrazowych, przy czym podział odnosi się bardziej do
sposobu przedstawiania danych obrazowych i ich
przedstawiania niż do formy wizualnej.
– Rozróżnia się cztery klasy obrazów:
Obrazy pełnokolorowe (I klasa),
dwu lub kilkukolorowe (II klasa),
Odcinki lub krzywe ciagłe (III klasa),
Punkty izolowane i wieloboki (IV klasa).
13. obrazy o pełnej gradacji kontrastów i kolorowe
• obrazy są reprezentowane jako macierze zelementami zwanymi pixelami.
• Macierze są znacznych rozmiarów -typowe
mają 512x512 i dlatego często są
przechowywane nie jako zwykłe macierze, ale
z wykorzystaniem bardziej wyszukanych form.
• Ewentualne kolory mogą być uwzględniane
jako macierze trójwymiarowe. Przykładem
obrazów tej klasy są np. obrazy telewizyjne.
14. obrazy dwupoziomowe lub kilkukolorowe
• obrazy tej klasy są zapamiętywane jakomacierze z jednym bitem na element obrazu.
• Obrazy kilkukolorowe są pamiętane jako mapy
zawierające jednoznacznie zdefiniowane
obszary o ustalonym kolorze.
• Przykładem obrazu dwupoziomowego może
być strona tekstu.
15. krzywe ciągłe i linie proste
obraz jest ciągiem punktów, które mogą być
reprezentowane przez współrzędne (x,y) danego
punktu lub poprzez przyrosty Dx, Dy między
kolejnymi punktami.
Efektywniejszą metodą jest jednak
wykorzystywanie kodów łańcuchowych, w
którym poszczególnym kierunkom
przyporządkowujemy odpowiednie symbole.
Jeszcze wydajniejszą metodą jest stosowanie
różnicowego kodu łańcuchowego. Przykład:
– metoda współrzędnych:
(12,13),(13,13),(13,14),(12,15)
– metoda przyrostowa: (12,13), (1,0), (0,1),(-1,1)
– metoda kodów łańcuchowych: (12,13),0,1,3 gdy
kierunkowi w prawo przypiszemy 0, kierunkowi
prawo do góry przypiszemy 1, kierunkowi lewo do
góry 3, rysunek
1
+1
0
-1
7
16. krzywe ciągłe i linie proste - cd
• metoda różnicowego kodułańcuchowego wykorzystuje różnice
dla między poszczególnymi kodami
łańcuchowymi. Mamy więc
wartości: 0, +1, -1, +2, -2, +3, -3 4.
• Dla krzywych gładkich pewne
różnice występują częściej niż
pozostałe. Aby przedstawić rysunek
możemy wtedy użyć kodu o
zmiennej długości, np.
Kierunek
Kod
0
0
+1
01
-1
011
+2
0111
-2
01111
+3
011111
-3
0111111
4
01111111
17. punkty lub wieloboki
• Obrazy klasy czwartej są reprezentowane przez oddzielne zbiorypunktów, które są tak odległe, że nie mogą być reprezentowane
przez kody łańcuchowe. Należy wtedy zastosować tablicę
współrzędnych (x,y), a do tej tablicy można zastosować jeszcze
kody przyrostowe lub kody różnicowe. Punkty mogą być
połączone za pomocą linii prostych lub krzywych. Liczba punktów
określająca położenie obiektu jest mała. Obrazy tego typu są
najczęściej stosowane w grafice komputerowej. W większości
zastosowań stosuje się następujące metody:
– aproksymacja powierzchni za pomocą wieloboków, wycinki
aproksymowane są zwykle trójkątami. Obraz składa się wtedy z
wieloboków,
– krzywoliniowe przybliżanie kształtu powierzchni, zbiór krzywych jest
rysowany na powierzchni bryły, a ich opisy są używane do otrzymania
rzutów,
– wycinki powierzchni wyższego rzędu, zamiast płaskich wieloboków do opisu
powierzchni bryły wykorzystywane są wycinki powierzchni wyższego rzędu.
18. Przekształcenia miedzy klasami
• Klasa 1 w klasę 2. Taki proces nazywamy segmentacją i identyfikuje onobszary, gdzie kolor i jasność są w przybliżeniu jednakowe.
• Klasa 2 w klasę 3. Możliwe przekształcenia to znajdowanie konturu (obszar
odwzorowywany jest w krzywą zamkniętą) i ścienianie (tworzony jest zbiór
zwany szkieletem obrazu).
• Klasa 3 w klasę 4. Proces ten nazywany jest segmentacją krzywych. Ma on
na celu znalezienie punktów krytycznych na konturze, np. punktami
krytycznymi dla wielokątów są ich wierzchołki.
• Klasa 4 w klasę 3. Obejmuje on interpolację, w której krzywa gładka
przechodzi przez punkty i aproksymację, gdy krzywa gładka przechodzi w
pobliżu punktów.
• Klasa 3 w klasę 2. Obejmuje zagadnienia wypełniania konturów (nazywane
jest to czasem cieniowaniem). Jeżeli na wejściu jest szkielet obiektu to
obraz musi być zrekonstruowany poprzez rozszerzanie.
• Klasa 2 w klasę 1. Przejście między tymi klasami polega na poprawieniu
estetyki obrazu, osiąga się to poprzez zastosowanie filtrów
dolnoprzepustowych lub z zastosowaniem filtrów zakłócających drżenie
kolorów
19. Inne przekształcenia
• Przedstawione wcześniej przekształcenia obrazówobejmują rozpoznawanie obrazów dla przejścia z klasy
niższej do klasy wyższej oraz grafikę komputerową dla
przekształcenia obrazu z klasy wyższej do klasy niższej.
• Innymi przekształceniami są mogą być przekształcenia
wewnątrz klasowe -przykładem może być polepszanie
jakości obrazu.
• Ważną klasą zagadnień stanowią przekształcenia między
obrazami dwuwymiarowymi a obrazami
trójwymiarowymi. Obejmują one rzutowanie - przejście
od obrazu trójwymiarowego do dwuwymiarowego i
reprojekcja - rekonstrukcja obrazu trójwymiarowego na
podstawie rzutów.
• Inną klasą zastosowań są przekształcenia geometryczne
obiektów. Rozważa się także przy nich problemy
20. grafika rastrowa - wikipedia
• Grafika rastrowa: prezentacja obrazu zapomocą pionowo-poziomej siatki
odpowiednio kolorowanych pikseli na
monitorze komputera, drukarce lub innym
urządzeniu wyjściowym.
• O rozdzielczości systemu (minimalna
odległość między dwoma punktami na
ekranie) decyduje elektronika układów
stosowanych do pisania na ekranie.
Dlatego też stosowane są układy o matrycy
ekranu o wymiarach 4096x4096. Dla
urządzeń rastrowych musi istnieć
odwzorowanie elementów obrazu na
komórki pamięci operacyjnej. Zwiększenie
rozdzielczości powoduje zwiększenie
potrzebnej ilości pamięci. Obecnie
spotykane matryce ekranu mają wymiar
1024x1024. Mniejsza rozdzielczość
powoduje efekt schodów przy rysowaniu
linii ukośnych
21. Grafika wektorowa - wikipedia
• jeden z dwóch podstawowych rodzajów grafiki komputerowej, w którejobraz opisany jest za pomocą figur geometrycznych (w przypadku grafiki
dwuwymiarowej) lub brył geometrycznych (w przypadku grafiki
trójwymiarowej), umiejscowionych w matematycznie zdefiniowanym
układzie współrzędnych, odpowiednio dwu- lub trójwymiarowym,
• Druga nazwa grafiki wektorowej – grafika obiektowa – związana jest z
faktem, iż obraz opisany jest za pomocą tzw. obiektów, które zbudowane
są z podstawowych elementów nazywanych prymitywami, czyli prostych
figur geometrycznych takich jak odcinki, krzywe, okręgi, wielokąty. Każdy z
prymitywów opisywany jest za pomocą parametrów, np. w przypadku
odcinka – współrzędnych jego końców, a w przypadku okręgu –
współrzędnych środka i długości promienia. Obiekty takie mają także
określone atrybuty mówiące np. o grubości i kolorze linii, kolorze
wypełnienia figury lub wypełnieniu niejednolitym jak wypełnienie
gradientem albo wzorem, stopniu przezroczystości. Atrybuty zależą
głównie od stosowanego standardu opisu grafiki wektorowej.
22. Porównanie grafiki wektorowej i rastrowej
• Obrazy I i II klasy należą do grafiki rastrowej.• Obrazy klasy III i IV należą do grafiki wektorowej.
• Zaletą grafiki wektorowej jest oddzielenie opisu
obiektu od ekranu.
23. Problemy grafiki komputerowej
• Operacje na danych (rysowanie, wypełnianie, triangulacje, wyznaczaniezbiorów punktów, przekształcenia geometryczne, reprezentacje: drzewa
czwórkowe, ósemkowe, reprezentacje wieloscienne)
• Modelowanie świata rzeczywistego,
• Wizualizacja modeli,
• Realizm,
• Symulacje zjawisk fizycznych (jest zawężeniem problemu modelowania),
np.
–
–
–
–
–
–
–
Ruch kuli,
Ruch dwu kul,
Kolizje dwu kul,
Zderzenie sprężyste (bez deformacji),
Zderzenie plastyczne (deformacja),
Zderzenie sprężysto-lepkoplastyczne,
Modele behavioralne: symulacja ruchu ławicy ryb, stada ptaków.






















 software
software
