Trend analizi
1. TREND ANALİZİ
KHAKIM GABBASSOV161125013
2. TREND KAVRAMI
• Trend tahmini verilerin yorumlanmasına yardımeden istatistiksel bir tekniktir.
• Zaman serisi analizlerinde güdülen amaç
geçmişten yararlanılarak geleceğin tahmin
edilmesidir.
• Bir firma yöneticisi elindeki son on beş aya ait
satış rakamlarına bakarak geleceğe yönelik
tahminde bulunabilir. Yöneticinin elindeki
verilerde geçmişte genel olarak satışlar
artmışsa, öyleyse gelecekte de bu durumun
sürmesi beklenir. İşte zaman serisinin en önemli
unsuru olan bu gidişe “trend” adı verilir.
3. Zaman Serisi Analizi
Doğrusal trend analizi olarak da bilinir. Özetle,zaman-trend analizi geçmiş yıllarda gerçekleşen
gözlem değerlerine “y = a + bx” modeli biçimindeki
en iyi uyan doğruyu, sapmaların karelerinin
toplamını minimize eden “En Küçük Kareler”
yöntemi ile belirlemeyi hedefler.
Daha sonra, doğrusal olduğu kabul edilen trendin
(eğilimin) gelecekte de devam edeceği varsayımı
altında tahminlerde bulunulur.
3
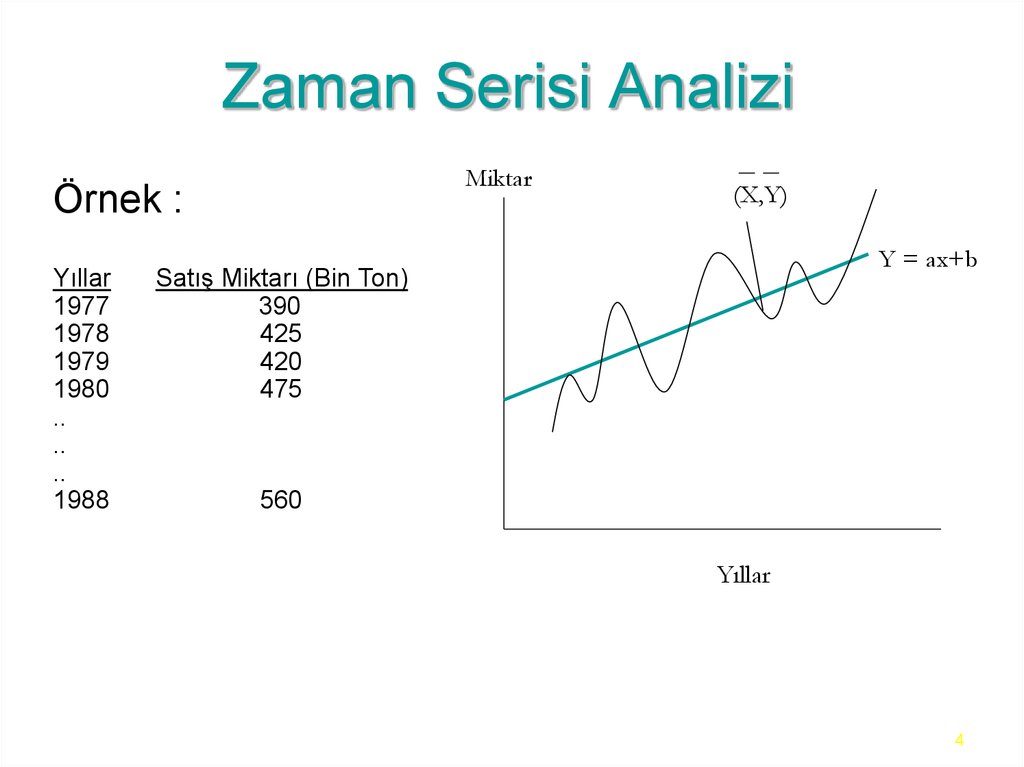
4. Zaman Serisi Analizi
MiktarÖrnek :
Yıllar
1977
1978
1979
1980
..
..
..
1988
(X,Y)
Y = ax+b
Satış Miktarı (Bin Ton)
390
425
420
475
560
Yıllar
4
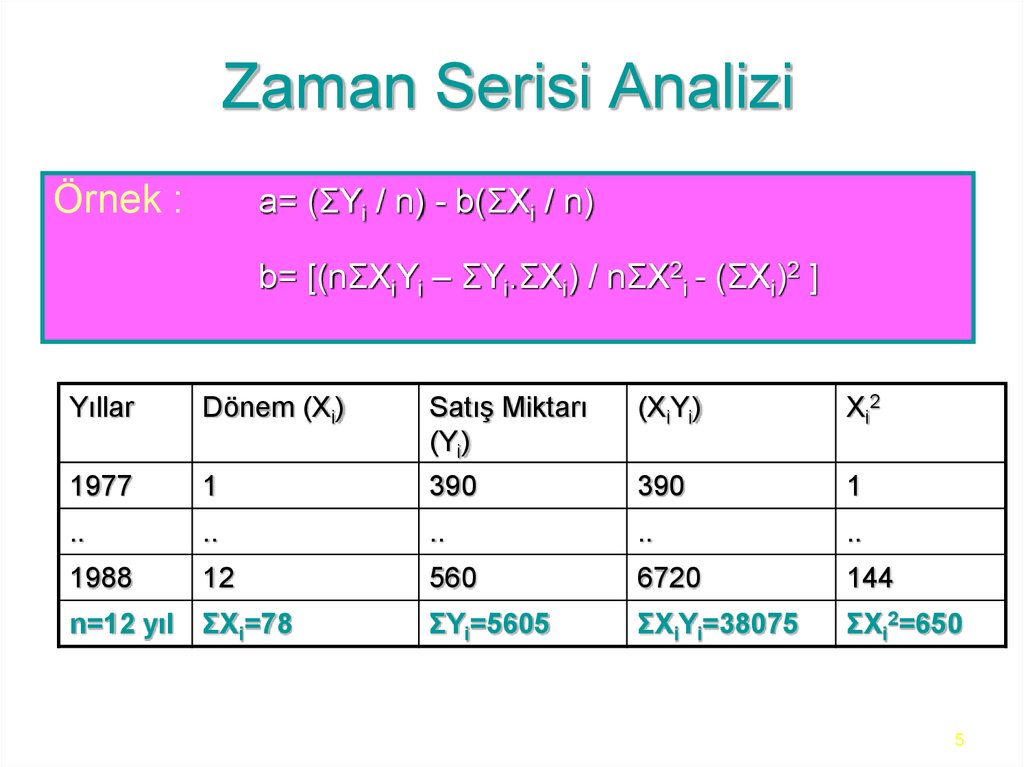
5. Zaman Serisi Analizi
Örnek :a= (ΣYi / n) - b(ΣXi / n)
b= [(nΣXiYi – ΣYi.ΣXi) / nΣX2i - (ΣXi)2 ]
Yıllar
Dönem (Xi)
Satış Miktarı
(Yi)
(XiYi)
Xi2
1977
1
390
390
1
..
..
..
..
..
1988
12
560
6720
144
ΣYi=5605
ΣXiYi=38075
ΣXi2=650
n=12 yıl ΣXi=78
5
6. Zaman Serisi Analizi
Örnek :Buradan,
b= [(12 (38075)- 78 (5605) / 12 (650) - (78)2]
b= 11.48 bulunur.
a= (5605 / 12) - (11.48 / 12)
a= 392.46 bulunur.
Katsayılarımız dikkate alındığında,
modelimiz şu şekilde ifade edilebilir :
doğrusal
tahmin
Y = 392.46 + 11.48 (X)
6
7. Zaman Serisi Analizi
Örnek :Y = 392.46 + 11.48 (X)
X = 13 yıl için ;
Y1989 = 392.46 + 11.48(13)
Y1989 = 541.7 bin ton
olarak tahmin edilir.
7
8.
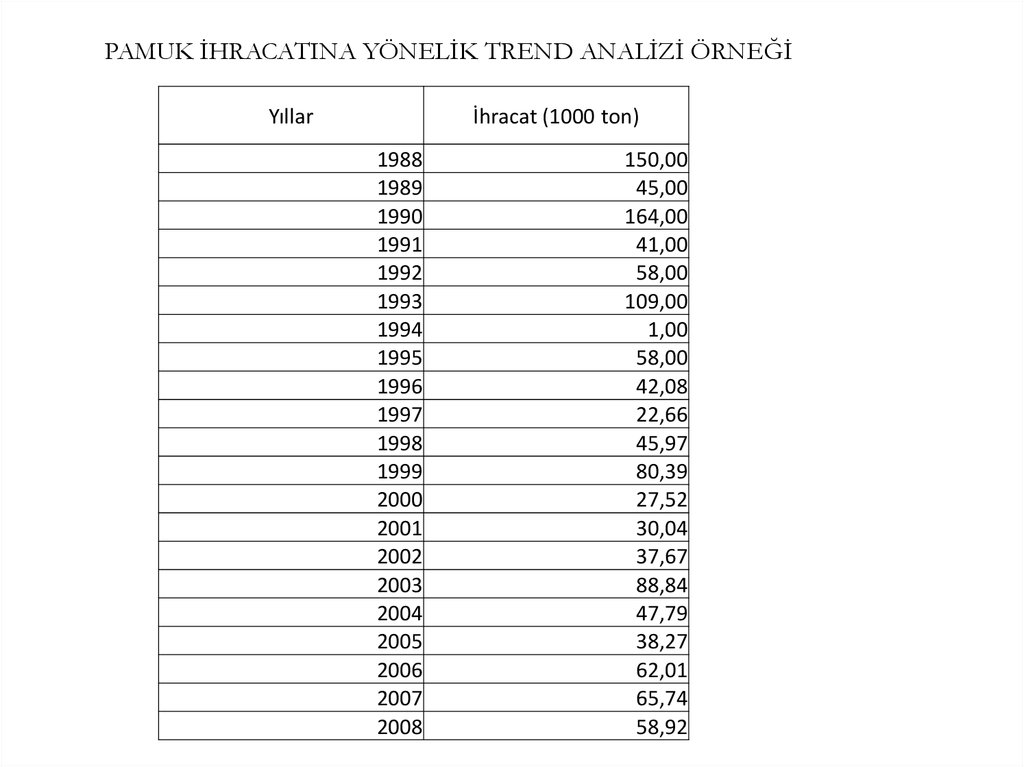
PAMUK İHRACATINA YÖNELİK TREND ANALİZİ ÖRNEĞİYıllar
İhracat (1000 ton)
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
150,00
45,00
164,00
41,00
58,00
109,00
1,00
58,00
42,08
22,66
45,97
80,39
27,52
30,04
37,67
88,84
47,79
38,27
62,01
65,74
58,92
9. Doğrusal Bir Trend İçin Genel Denklem
F=a+btVeya
Y=a+bx
• F – forecast
(tahmin)
• t – time value
(zaman değeri),
• a – y intercept (sabit
katsayı),
• b – Doğrunun eğimi.
9
10. En Küçük Kareler Yöntemi
• Bu yöntemle tarihsel veriler kullanılarak enuygun doğru belirlenir. Bu amaçla a ve b
katsayıları hesaplanır.
• a ve b katsayıları belirlendikten sonra,
oluşturulan denklem ile gelecekteki değerler
tahmin edilir.
10
11.
a= (ΣYi / n) - b(ΣXi / n)b= [(nΣXiYi – ΣYi.ΣXi) / nΣX2i - (ΣXi)2 ]
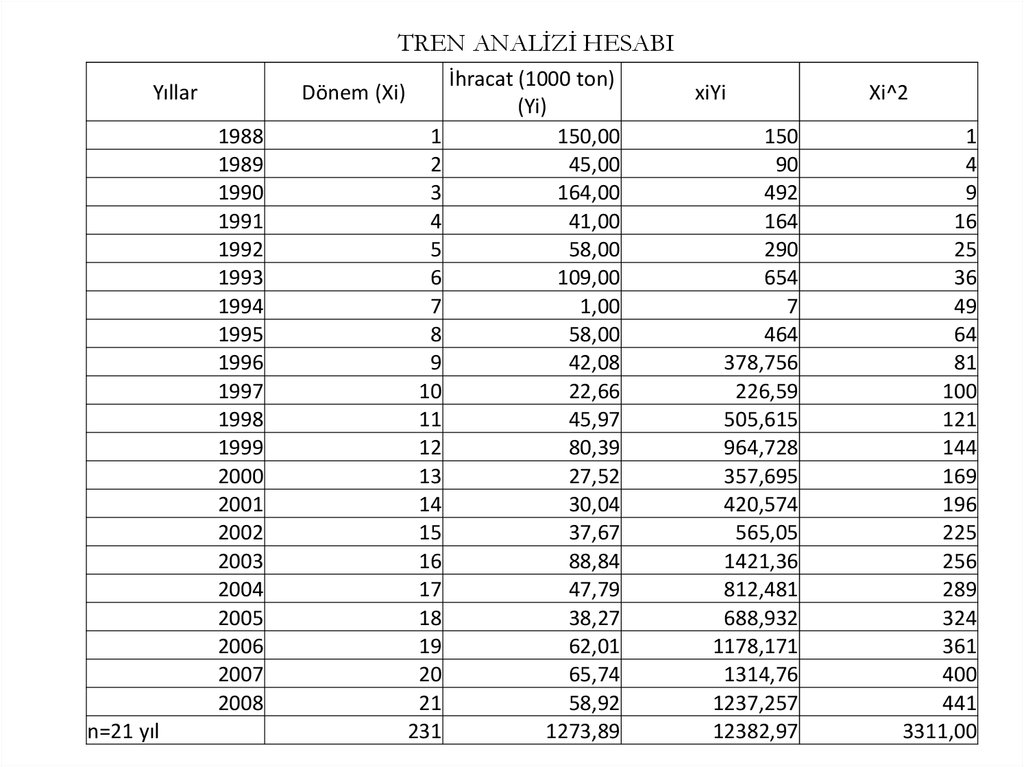
12.
TREN ANALİZİ HESABIYıllar
Dönem (Xi)
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
n=21 yıl
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
231
İhracat (1000 ton)
(Yi)
150,00
45,00
164,00
41,00
58,00
109,00
1,00
58,00
42,08
22,66
45,97
80,39
27,52
30,04
37,67
88,84
47,79
38,27
62,01
65,74
58,92
1273,89
xiYi
150
90
492
164
290
654
7
464
378,756
226,59
505,615
964,728
357,695
420,574
565,05
1421,36
812,481
688,932
1178,171
1314,76
1237,257
12382,97
Xi^2
1
4
9
16
25
36
49
64
81
100
121
144
169
196
225
256
289
324
361
400
441
3311,00
13.
b=[(21*12382,97-1273,89*231)/21*3311-(231)^2]= - 2,11671a= (1273,89/21)-2,11671*(231/21)=83,94954
Y = -2,11671 x +83,94954
2009 yılı için tahmin Y = -2,11671 * (22) +83,94954 = 37,37783
14. Zaman Serisi Analizi
Önemli hususlar:1) Zaman serisi analizlerinde geçmiş verilerin
doğrusal bir trend izlemesi gerekir. Aksi halde,
doğrusal olmayan en iyi eğrilerin geçmiş verilere
uyarlanması şart olur.
2) Veriler alınırken, mevsimsel, devrevi ve rassal
değişimlerin belirlenmesi ve tahmin modelinin
anılan etkileri gözetecek şekilde kurulması
gereklidir.
3) Dönem uzunluğunun 12’den az sayıda
olmamasına dikkat edilmelidir.
14
15.
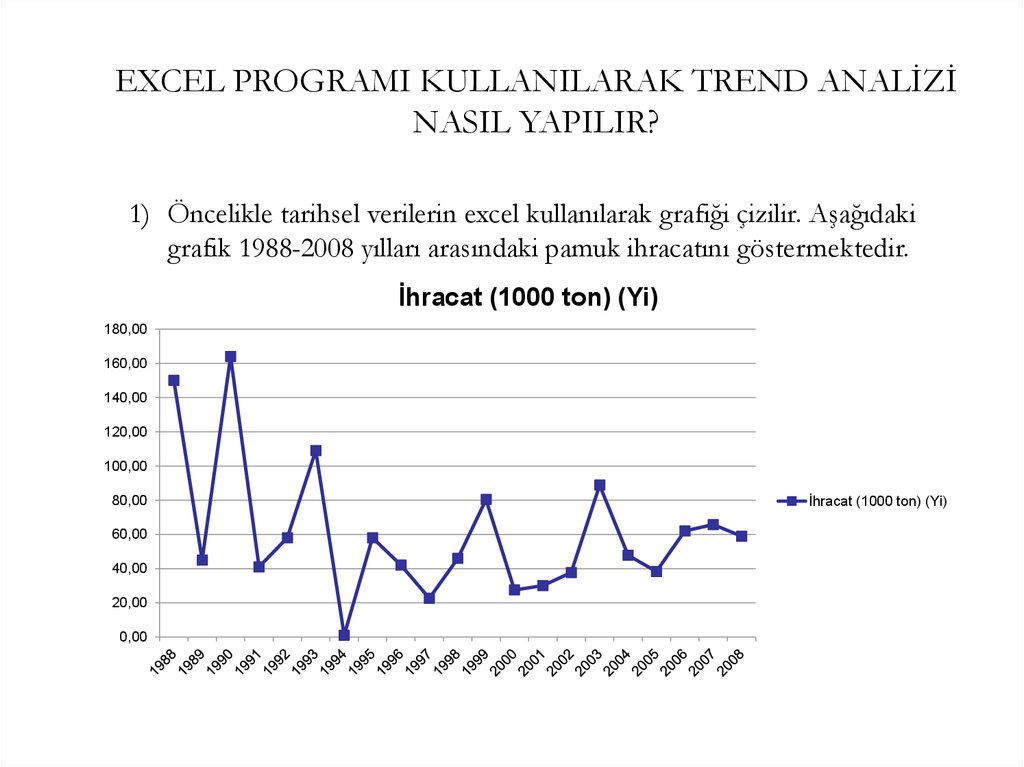
EXCEL PROGRAMI KULLANILARAK TREND ANALİZİNASIL YAPILIR?
1) Öncelikle tarihsel verilerin excel kullanılarak grafiği çizilir. Aşağıdaki
grafik 1988-2008 yılları arasındaki pamuk ihracatını göstermektedir.
İhracat (1000 ton) (Yi)
180,00
160,00
140,00
120,00
100,00
80,00
60,00
40,00
20,00
0,00
İhracat (1000 ton) (Yi)
16.
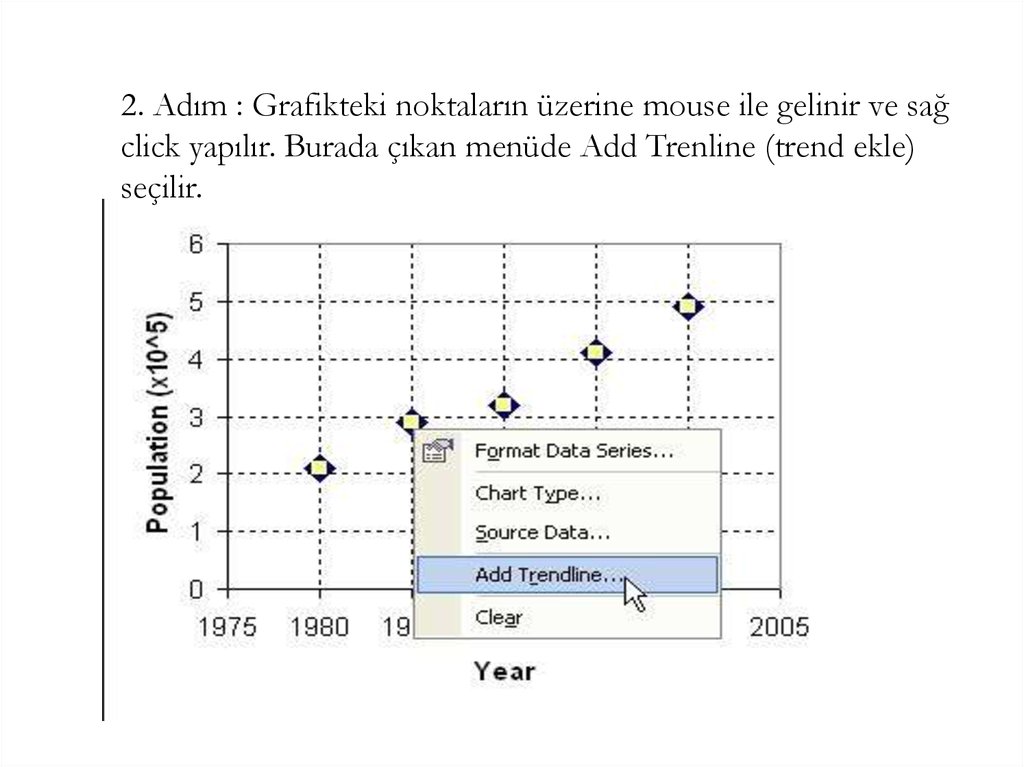
2. Adım : Grafikteki noktaların üzerine mouse ile gelinir ve sağclick yapılır. Burada çıkan menüde Add Trenline (trend ekle)
seçilir.
17.
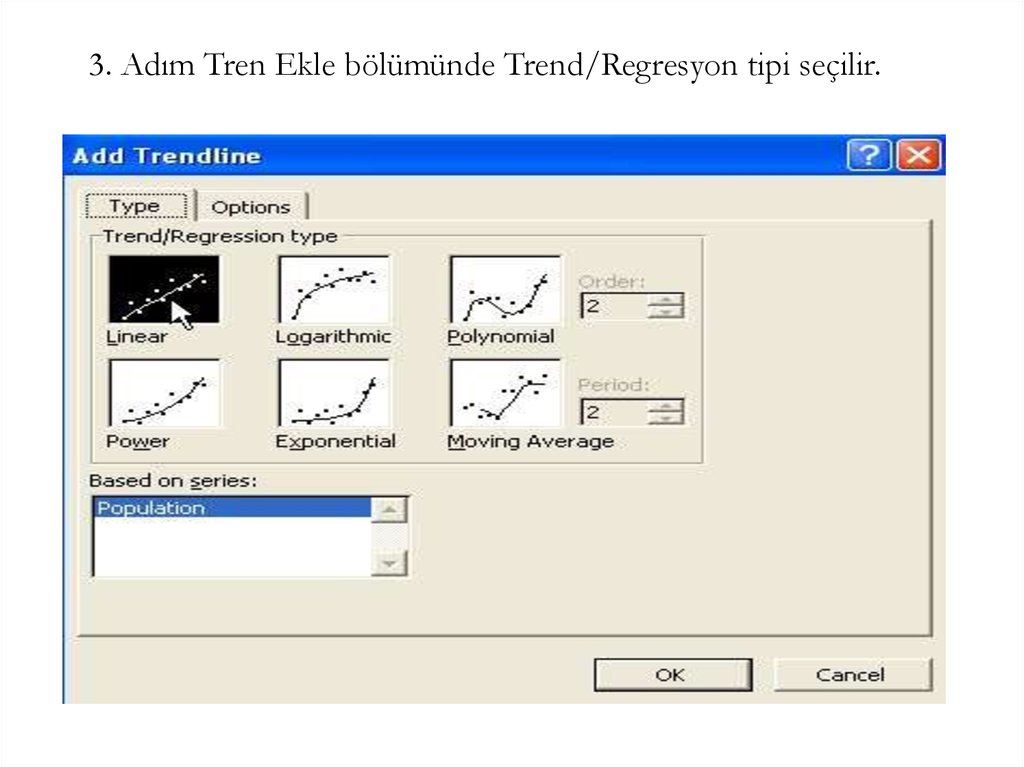
3. Adım Tren Ekle bölümünde Trend/Regresyon tipi seçilir.18.
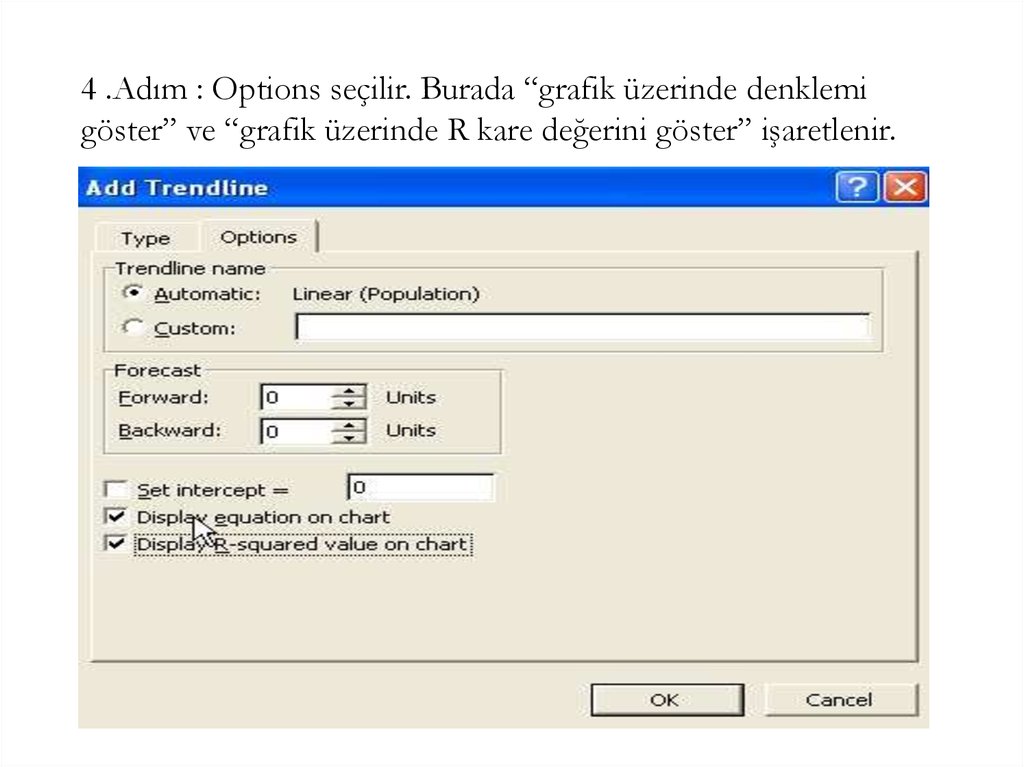
4 .Adım : Options seçilir. Burada “grafik üzerinde denklemigöster” ve “grafik üzerinde R kare değerini göster” işaretlenir.
19.
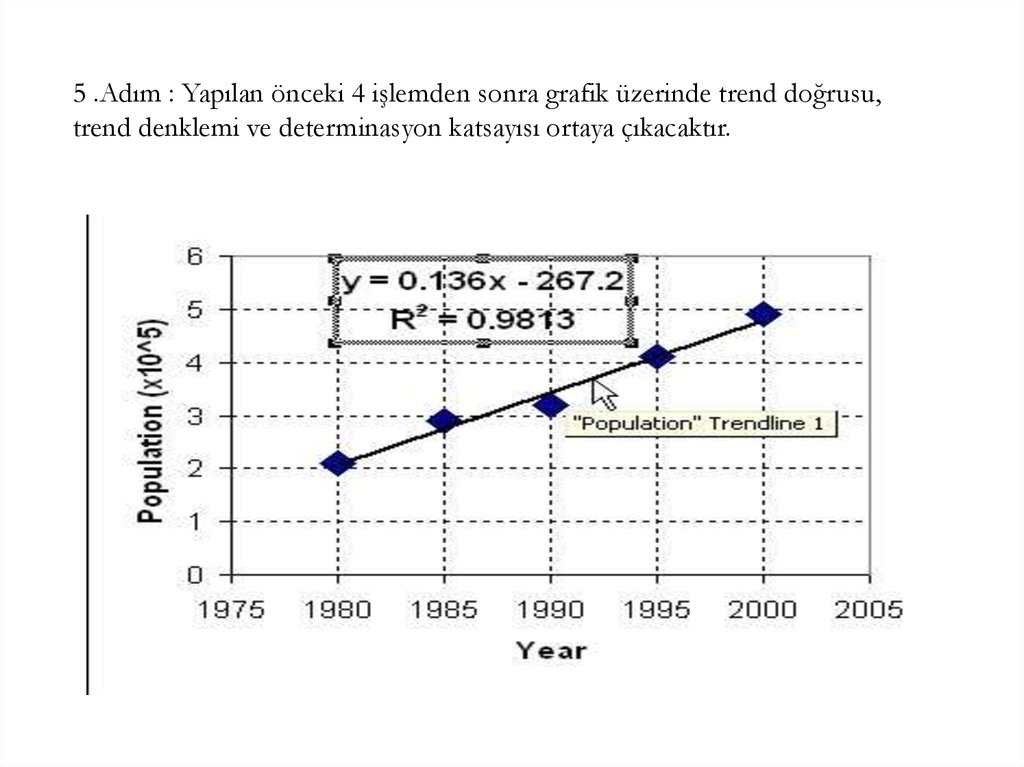
5 .Adım : Yapılan önceki 4 işlemden sonra grafik üzerinde trend doğrusu,trend denklemi ve determinasyon katsayısı ortaya çıkacaktır.
20.
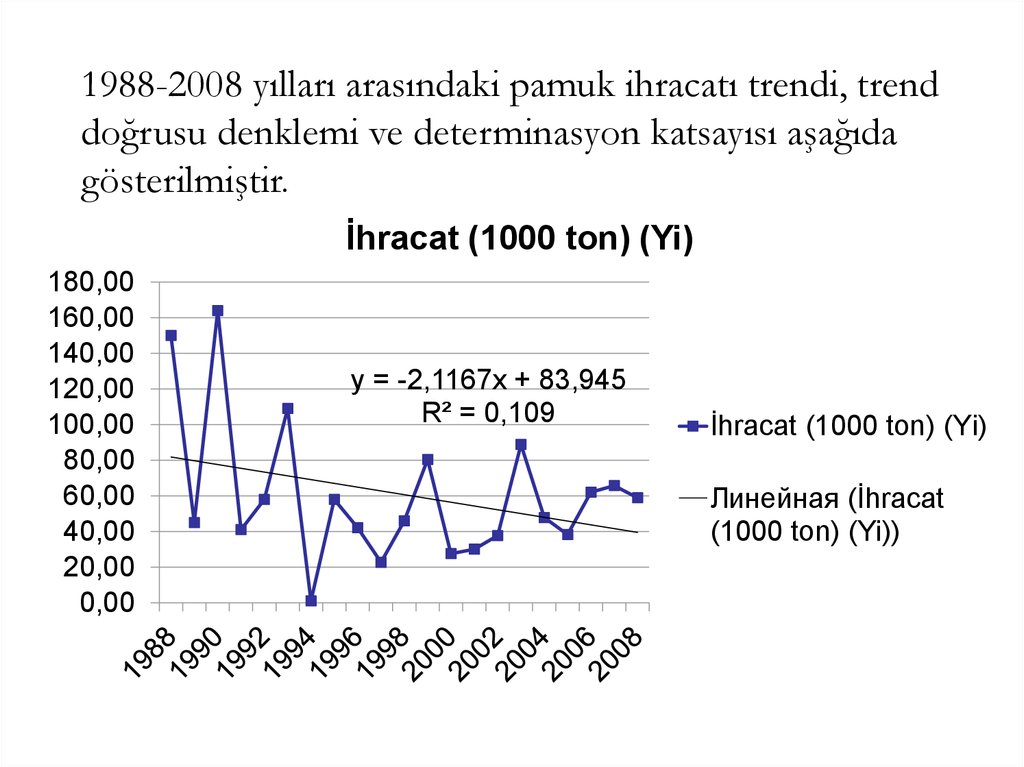
1988-2008 yılları arasındaki pamuk ihracatı trendi, trenddoğrusu denklemi ve determinasyon katsayısı aşağıda
gösterilmiştir.
İhracat (1000 ton) (Yi)
180,00
160,00
140,00
120,00
100,00
80,00
60,00
40,00
20,00
0,00
y = -2,1167x + 83,945
R² = 0,109
İhracat (1000 ton) (Yi)
Линейная (İhracat
(1000 ton) (Yi))
21. Trend Analizlerinde Uyum İyiliğinin Ölçülmesinde ;
• Korelasyon Katsayısı (The CorrelationCoefficient)
ve
• Determinasyon Katsayısı (The
Determination Coefficient) kullanılmaktadır.
21
22. Determinasyon Katsayısı (R2)
• Regresyon veya trend doğrusutarafından açıklanan bağımlı
değişkendeki değişkenliğin yüzdesini
ölçmektedir. 0 ile 1 arasında değer
almaktadır, yüksek değer iyi bir uyum
olduğunu göstermektedir.
• Range: [0, 1].
• RSQ=1 means best fitting (iyi uyum)
• RSQ=0 means worse fitting (kötü uyum)
22
23. Doğrusal Olmayan Trendler (Non-linear trends)
Logarythmic (Logaritmik)
Polynomial (Polinom)
Power (güç)
Exponential (üssel)
Moving average (hareketli ortalamalar)
Quantitative forecasting methods
in library management
23
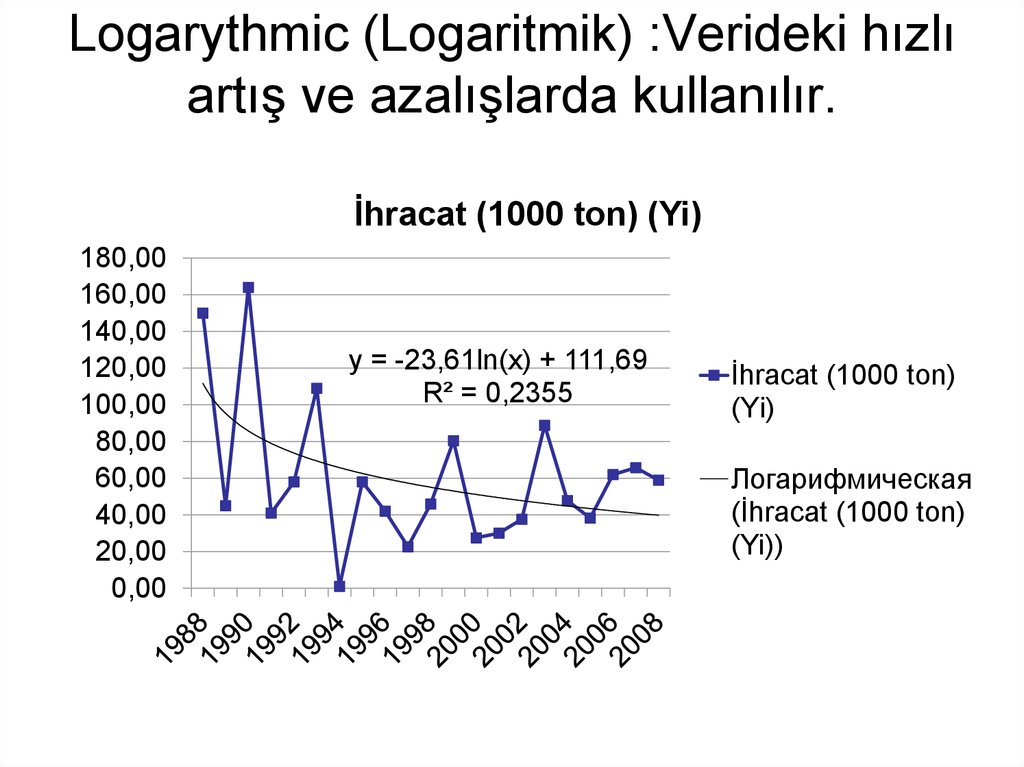
24. Logarythmic (Logaritmik) :Verideki hızlı artış ve azalışlarda kullanılır.
İhracat (1000 ton) (Yi)180,00
160,00
140,00
120,00
100,00
80,00
60,00
40,00
20,00
0,00
y = -23,61ln(x) + 111,69
R² = 0,2355
İhracat (1000 ton)
(Yi)
Логарифмическая
(İhracat (1000 ton)
(Yi))
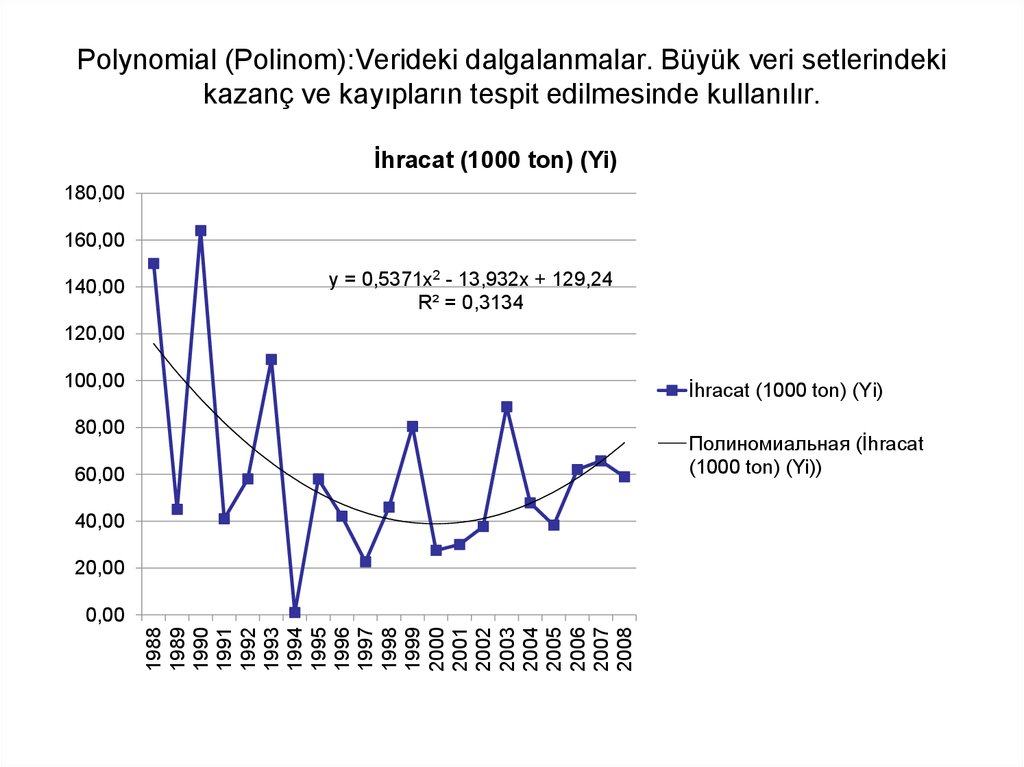
25. Polynomial (Polinom):Verideki dalgalanmalar. Büyük veri setlerindeki kazanç ve kayıpların tespit edilmesinde kullanılır.
İhracat (1000 ton) (Yi)180,00
160,00
140,00
y = 0,5371x2 - 13,932x + 129,24
R² = 0,3134
120,00
100,00
İhracat (1000 ton) (Yi)
80,00
Полиномиальная (İhracat
(1000 ton) (Yi))
60,00
40,00
20,00
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
0,00
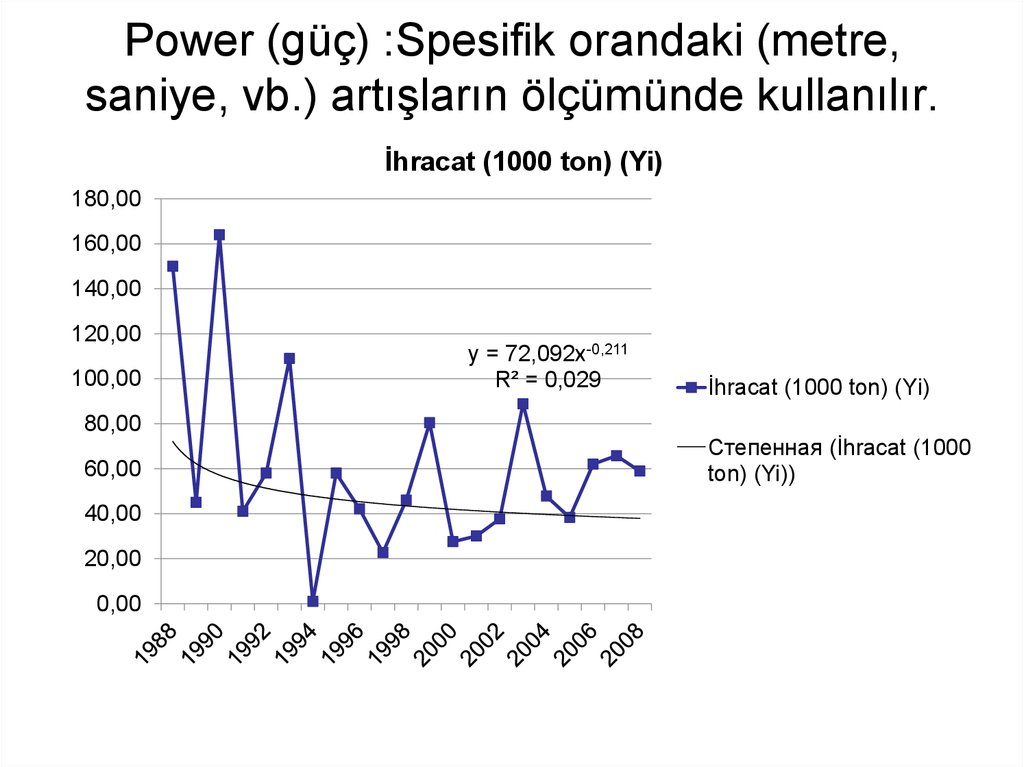
26. Power (güç) :Spesifik orandaki (metre, saniye, vb.) artışların ölçümünde kullanılır.
İhracat (1000 ton) (Yi)180,00
160,00
140,00
120,00
100,00
80,00
60,00
40,00
20,00
0,00
y = 72,092x-0,211
R² = 0,029
İhracat (1000 ton) (Yi)
Степенная (İhracat (1000
ton) (Yi))
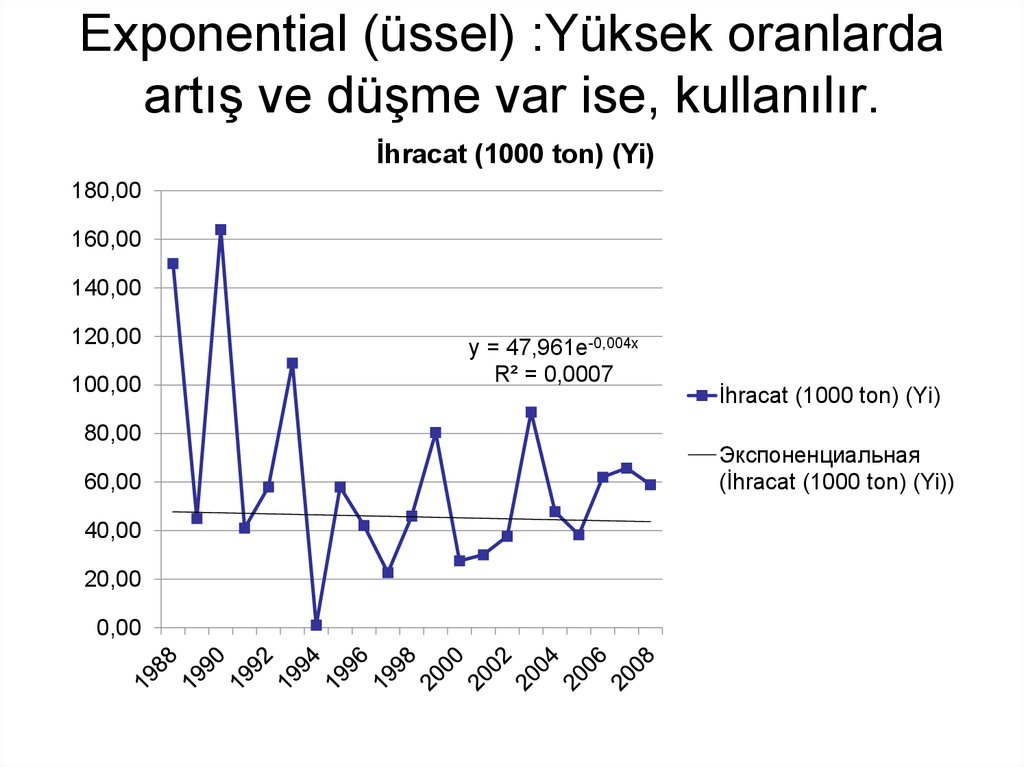
27. Exponential (üssel) :Yüksek oranlarda artış ve düşme var ise, kullanılır.
İhracat (1000 ton) (Yi)180,00
160,00
140,00
120,00
100,00
80,00
60,00
40,00
20,00
0,00
y = 47,961e-0,004x
R² = 0,0007
İhracat (1000 ton) (Yi)
Экспоненциальная
(İhracat (1000 ton) (Yi))
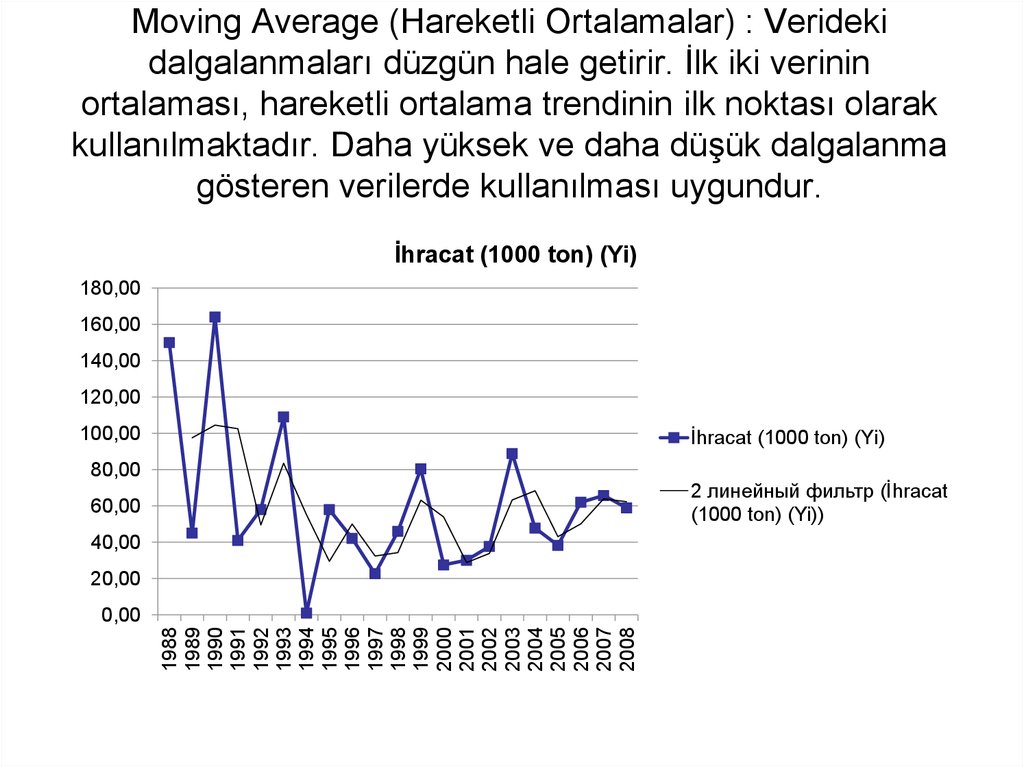
28. Moving Average (Hareketli Ortalamalar) : Verideki dalgalanmaları düzgün hale getirir. İlk iki verinin ortalaması, hareketli ortalama trendinin ilk noktası olarak kullanılmaktadır. Daha yüksek ve daha düşük dalgalanma gösteren verilerde kullan
Moving Average (Hareketli Ortalamalar) : Veridekidalgalanmaları düzgün hale getirir. İlk iki verinin
ortalaması, hareketli ortalama trendinin ilk noktası olarak
kullanılmaktadır. Daha yüksek ve daha düşük dalgalanma
gösteren verilerde kullanılması uygundur.
İhracat (1000 ton) (Yi)
180,00
160,00
140,00
120,00
100,00
İhracat (1000 ton) (Yi)
80,00
2 линейный фильтр (İhracat
(1000 ton) (Yi))
60,00
40,00
20,00
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
0,00
29. En iyi trend nasıl belirlenir?
• 1) Veri seti için 5 trend karşılaştırılır(linear, logarythmic, polynomial, power,
exponential)
Örneğin; verilerdeki artış ve azalışlar
istikrarlı bir şekilde ise, doğrusal (linear)
trend seçilir. Eğer verilerdeki artış ve
azalışlar çok hızlı ise logaritmik trend
seçilir.
• 2) Determisayon katsayılarına bakılır ve
en yüksek olanı seçilir.
29
30. Trend Analizi İle Tahmin Metodunun Değerlendirilmesi
• Avantajları: Eğer uygun bilgisayarprogramı var ise, kullanmak kolaydır.
• Dezavantajları:
1) Her zaman uzun dönemli zaman
serilerine uygulanamaz. (Çünkü böyle
durumlarda birkaç tane trend söz
konusudur);
2) Mevsimsel ve konjonktürel veri
desenlerine uygulanamaz.
30







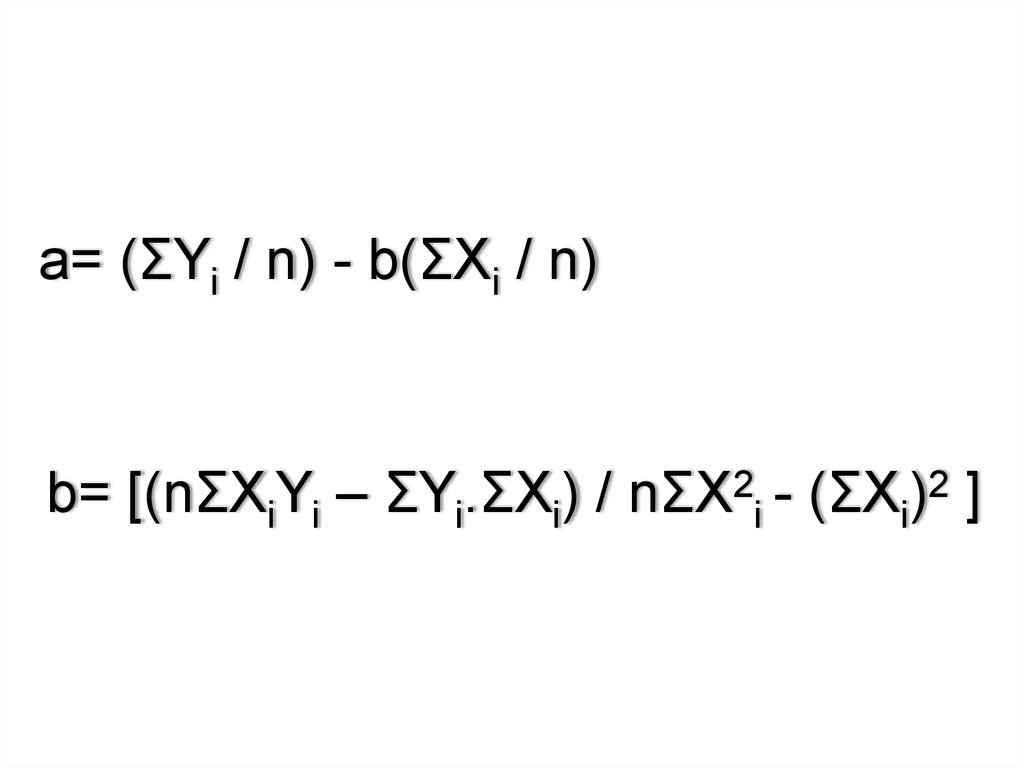







 management
management