Similar presentations:
Зеркальная симметрия и параллельный перенос
1.
Зеркальная симметрия и параллельный перенос.2.
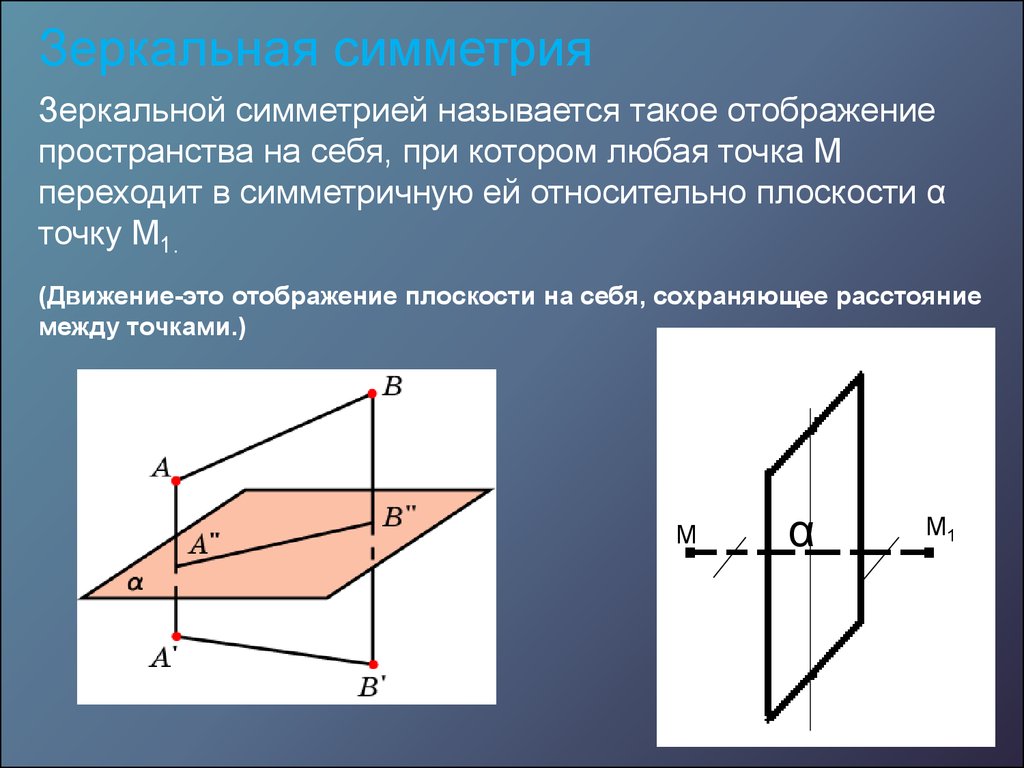
Зеркальная симметрияЗеркальной симметрией называется такое отображение
пространства на себя, при котором любая точка М
переходит в симметричную ей относительно плоскости α
точку М1.
(Движение-это отображение плоскости на себя, сохраняющее расстояние
между точками.)
М
α
α
М1
3.
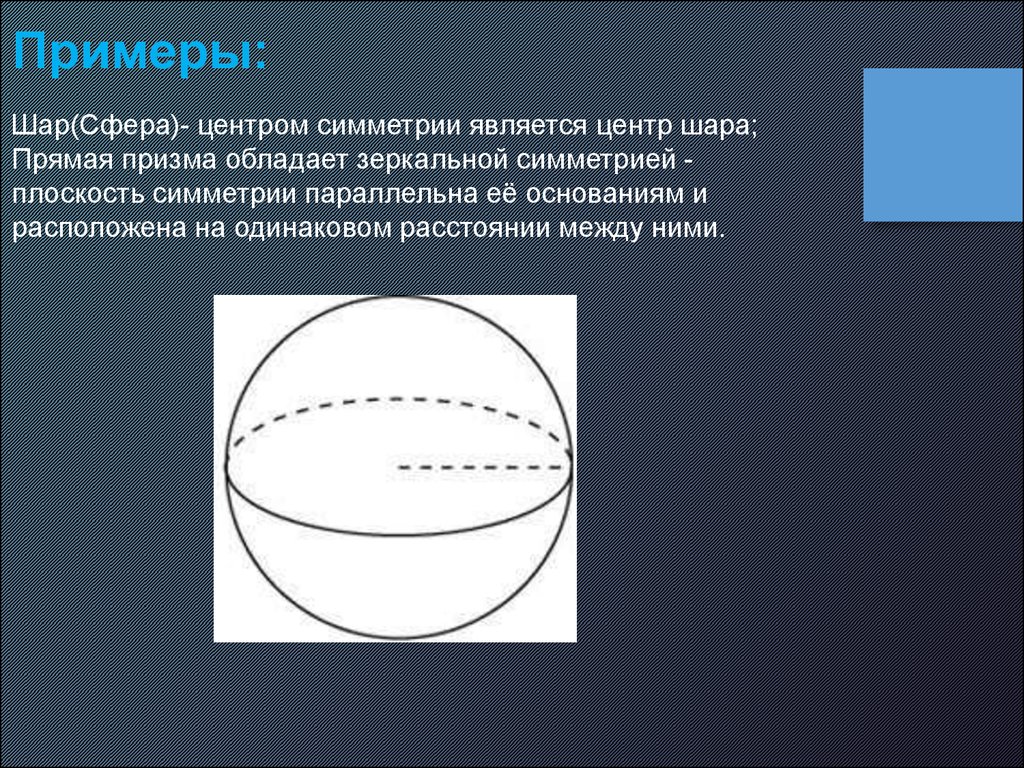
Примеры:Шар(Сфера)- центром симметрии является центр шара;
Прямая призма обладает зеркальной симметрией плоскость симметрии параллельна её основаниям и
расположена на одинаковом расстоянии между ними.
4.
Нотр-дам де Пари5.
Тадж-Махал6.
Параллельный переносПараллельным переносом в пространстве называется такое
преобразование, при котором произвольная точка (х; у; z) фигуры
переходит в точку (х+а; у+b; z+c), где числа а, b, c одни и те же
для всех точек (х; у; z). Параллельный перенос в пространстве задается
формулами x'=x+a, y'=y+b, z'=z+c. выражающими координаты х', у', z'
точки, в которую переходит точка (х; у; z) при параллельном переносе.
Так же, как и на плоскости, доказываются следующие свойства
параллельного переноса:
1. Параллельный перенос есть движение.
2. При параллельном переносе точки смещаются по параллельным (или
совпадающим) прямым на одно и то же расстояние.
3. При параллельном переносе каждая прямая переходит в параллельную
ей прямую (или в себя).
4. Каковы бы ни были точки А и А', существует единственный
параллельный перенос, при котором точка А переходит в точку А'.
Новым для параллельного переноса в пространстве является следующее
свойство:
5. При параллельном переносе в пространстве каждая плоскость переходит
либо в себя, либо в параллельную ей плоскость.
7.
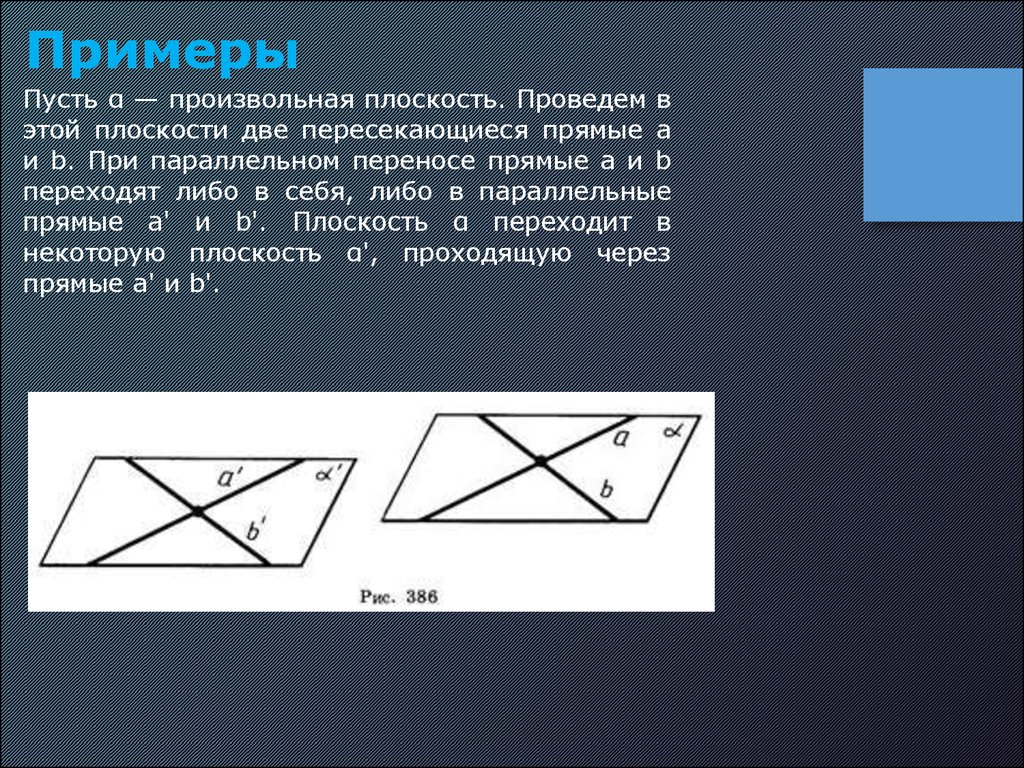
ПримерыПусть α — произвольная плоскость. Проведем в
этой плоскости две пересекающиеся прямые а
и b. При параллельном переносе прямые a и b
переходят либо в себя, либо в параллельные
прямые a' и b'. Плоскость α переходит в
некоторую плоскость α', проходящую через
прямые а' и b'.







 mathematics
mathematics








