Similar presentations:
Моделирование корреляционной зависимости с использованием инструментов EXCEL
1.
Практическая работа №3Моделирование корреляционной зависимости с
использованием инструментов EXCEL
1
2.
1. Моделирование однофакторной линейной регрессии y/tНа графике
1.1 Вставить ТОЧЕЧНУЮ ДИАГРАММУ (yi , ti).
1.2 Выделить точки исходных данных.
1.3 Добавить линию тренда.
2
3.
1.4 Во вкладке «Формат линии тренда» выбрать:–
вид аппроксимации – ЛИНЕЙНАЯ,
–
ПОКАЗЫВАТЬ УРАВНЕНИЕ НА
ДИАГРАММЕ,
–
ПОМЕСТИТЬ НА ДИАГРАММУ
ВЕЛИЧИНУ ДОСТОВЕРНОСТИ
АППРОКСИМАЦИИ R2
3
4.
2. Моделирование однофакторной линейной регрессии y/tс помощью функции ЛИНЕЙН
2.1 Выделить 10 ячеек (5*2).
2.2 Вставить функцию ЛИНЕЙН.
4
5.
2.3 Задать аргументы функции ЛИНЕЙН:ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Следует выделить ячейки с массивами значений Y и X.
При значении константы «ИСТИНА» будет вычислено значение константы b в
уравнении регрессии.
При заданном в поле [статистика] значении «ИСТИНА» будут вычислены
значения статистик, характеризующих точность модели.
5
6.
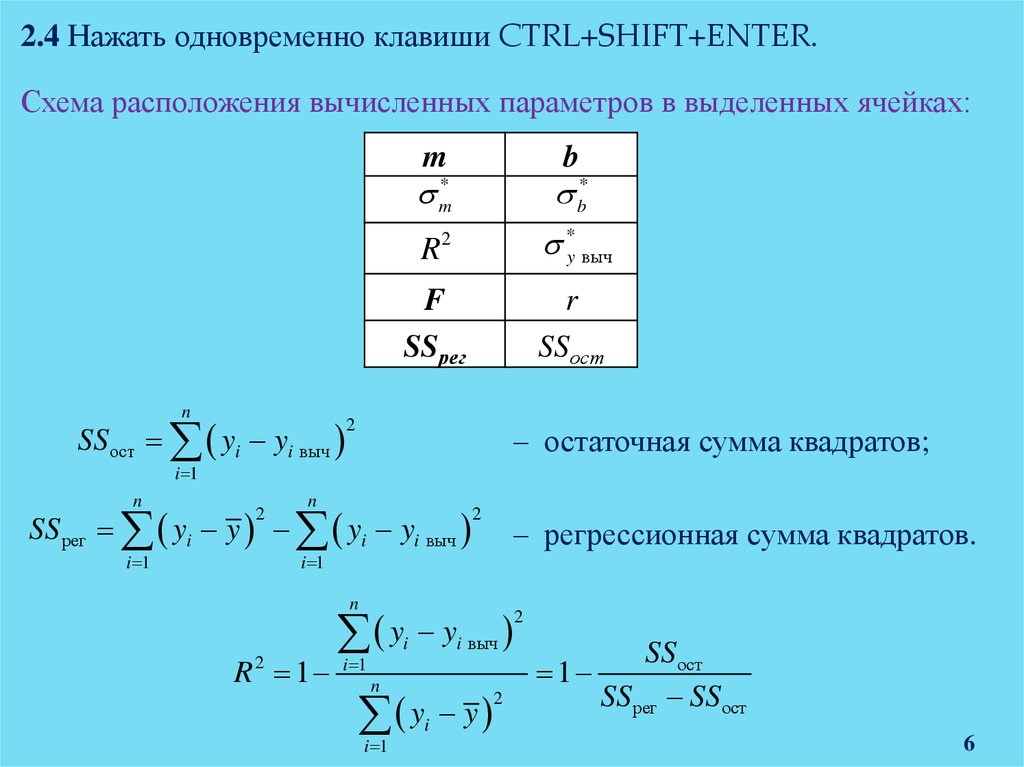
2.4 Нажать одновременно клавиши CTRL+SHIFT+ENTER.Схема расположения вычисленных параметров в выделенных ячейках:
n
SSост yi yi выч
m
m*
b
b*
R2
*y выч
F
SSрег
r
SSост
2
– остаточная сумма квадратов;
i 1
n
n
SS рег yi y yi yi выч
i 1
2
2
– регрессионная сумма квадратов.
i 1
n
R2 1
yi yi выч
i 1
n
yi y
i 1
2
2
1
SSост
SSрег SSост
6
7.
78.
3. Моделирование однофакторной нелинейной регрессиина графике
3.1 Во вкладке «Формат линии тренда» выбрать:
– вид аппроксимации –
ПОЛИНОМИАЛЬНАЯ, степень – 2,
– ПОКАЗЫВАТЬ УРАВНЕНИЕ НА
ДИАГРАММЕ,
– ПОМЕСТИТЬ НА ДИАГРАММУ
ВЕЛИЧИНУ ДОСТОВЕРНОСТИ
АППРОКСИМАЦИИ R2.
8
9.
3.2 Вычислим смоделированные значения yвычyi выч m1ti2 m2ti b 0,379ti2 10,884ti 63,911
3.3 Найдем истинные ошибки смоделированных значений:
i yi выч yi .
3.4 Оценим точность модели по формуле Гаусса
n
*y выч
i 1
n
2
i
2867,67
9,8
30
9
10.
4. Моделирование многофакторной линейной регрессиис помощью функции ЛИНЕЙН
y m1t m2 z b
4.1 Выделить 15 ячеек (5*3).
4.2 Вставить функцию ЛИНЕЙН.
10
11.
4.3 Задать аргументы функции ЛИНЕЙН:ЛИНЕЙН(известные_значения_y; [известные_значения_x1];
[известные_значения_x2];[известные_значения_x]; [конст]; [статистика])
Следует выделить ячейки с массивами значений y, t и z.
Задать значения константы и статистики «ИСТИНА».
11
12.
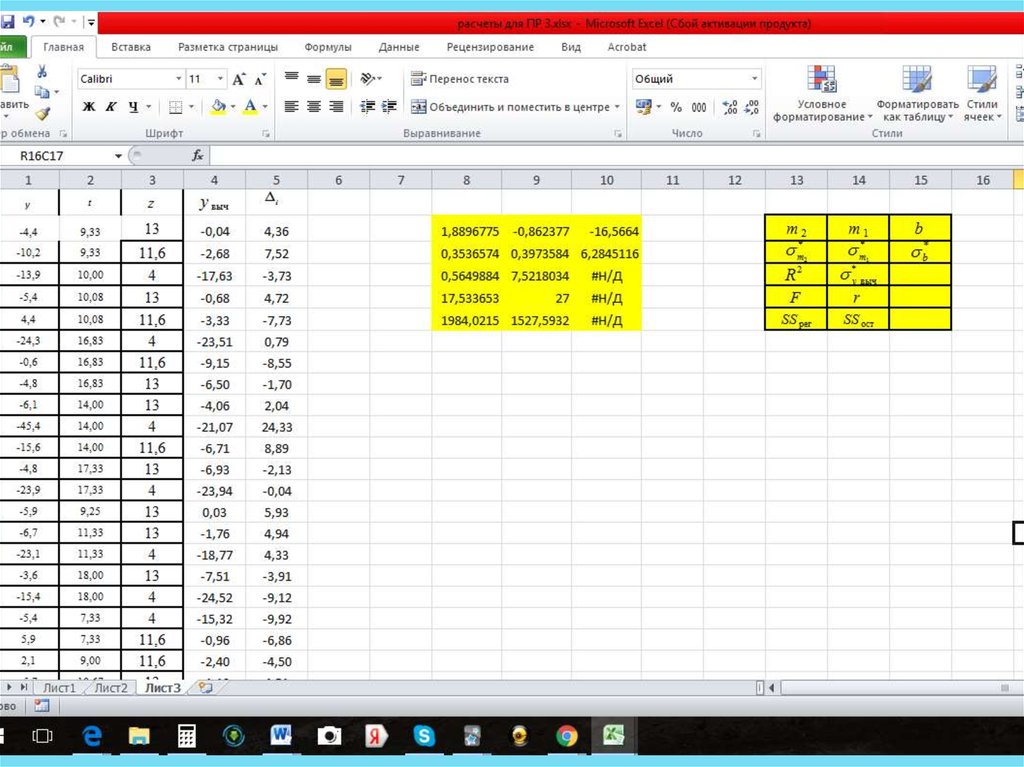
4.4 Нажать одновременно клавиши CTRL+SHIFT+ENTER.Схема расположения вычисленных параметров в выделенных ячейках:
m2
m1
b
m*
m*
b*
2
R
2
1
*y выч
F
r
SSрег
SSост
12
13.
1314.
5. Анализ полученных результатовТип модели
Уравнение регрессии
Линейная однофакторная
yi выч 1,012ti 3,910
R2
*y выч
0,105 10,6"
Нелинейная однофакторная
(полином 2-ой степени)
yi выч 0,379ti2 10,884ti 63,911 0,186
9,8"
Линейная двухфакторная
yi выч 1,890ti 0,862 zi 16,566 0,565
7,5"
Выводы
1. Набольшая точность получена для линейной двухфакторной
зависимости. Коэффициент множественной линейной корреляции:
Rytz R 2 0,565 0,75.
2. Использование данной модели позволит вдвое повысить точность:
n
y
2
i
5584,96
*y выч 7,5
13,6
n
30
3. Ни одна из моделей не позволяет получить угол рефракции с
геодезической точностью.
*
i 1
14












 informatics
informatics