Комплексные числа

1. КОМПЛЕКСНЫЕ ЧИСЛА

2. Элемент, квадрат которого равен -1 называется мнимой единицей. Обозначается i (переводится «мнимый», «воображаемый»)

"Комплексными числами и функциями
комплексного переменного математики пользовались
в своих исследованиях уже в XVIII в. Особенно
велики заслуги крупнейшего математика XVIII в.
Леонарда Эйлера (1707—1783), который по праву
считается одним из творцов теории функций
комплексного переменного. В замечательных работах
Эйлера детально изучены элементарные функции
комплексного
переменного.
После Эйлера открытые им результаты и методы
развивались,
совершенствовались
и
систематизировались, и в первой половине XIX в.
теория
функций
комплексного
переменного
оформилась
как
важнейшая
отрасль
Первое
изложение теории комплексных
чисел
на
русском
языке
принадлежит Л. Эйлеру («Алгебра»,
математического
анализа.
Петербург, 1763, позднее книга была переведена на
иностранные языки и многократно переиздавалась):
символ «i» также введен Л.
Эйлером. Геометрическая интерпретация
комплексных чисел относится к концу XVIII в.
(датчанин Каспар Вессель, 1799 г.)."

3.

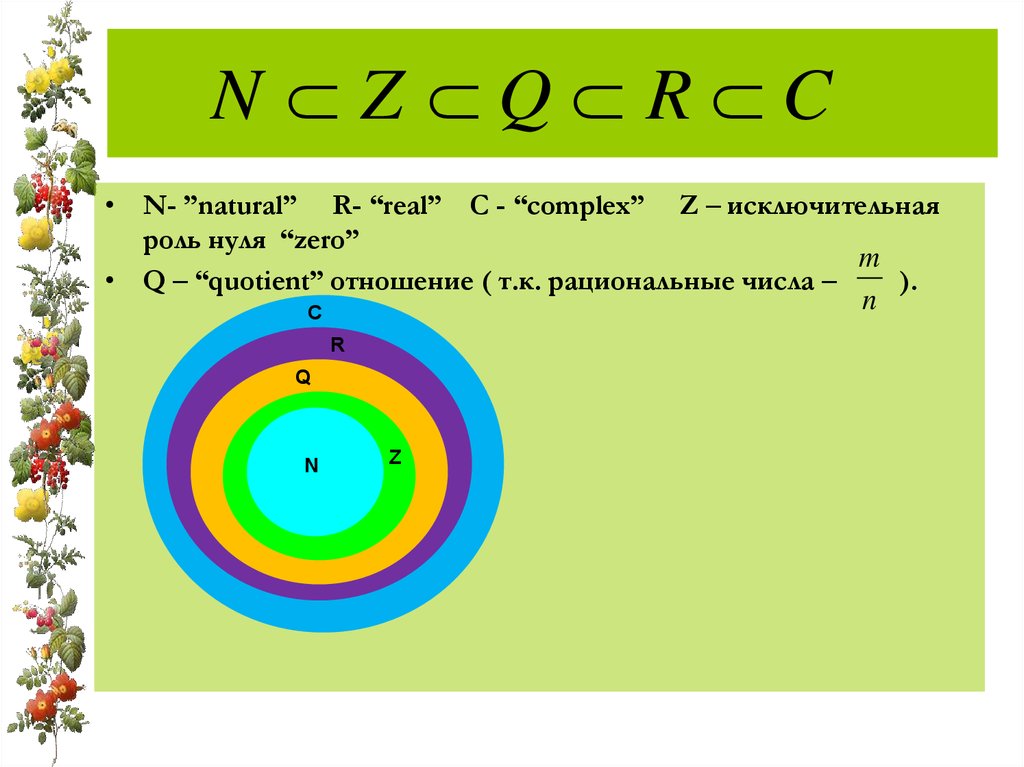
N Z Q R C
• N- ”natural” R- “real” C - “complex” Z – исключительная
роль нуля “zero”
m
• Q – “quotient” отношение ( т.к. рациональные числа –
).
n
C
R
Q
N
Z

4. Решение квадратных уравнений

ах²+ bx+ c =0
При D<0 действительных корней нет
Рациональные
числа
Иррациональные
числа
Действительные
числа
+

5. Вид комплексного числа

х² = -1
х = 1
х= i -корень уравнения
i- число, такое , что i² = -1
i – мнимая единица
Элемент i называется мнимой единицей. («imaginary» переводится «мнимый», «воображаемый»)

6.

д)
ж)
е)
з)

7.

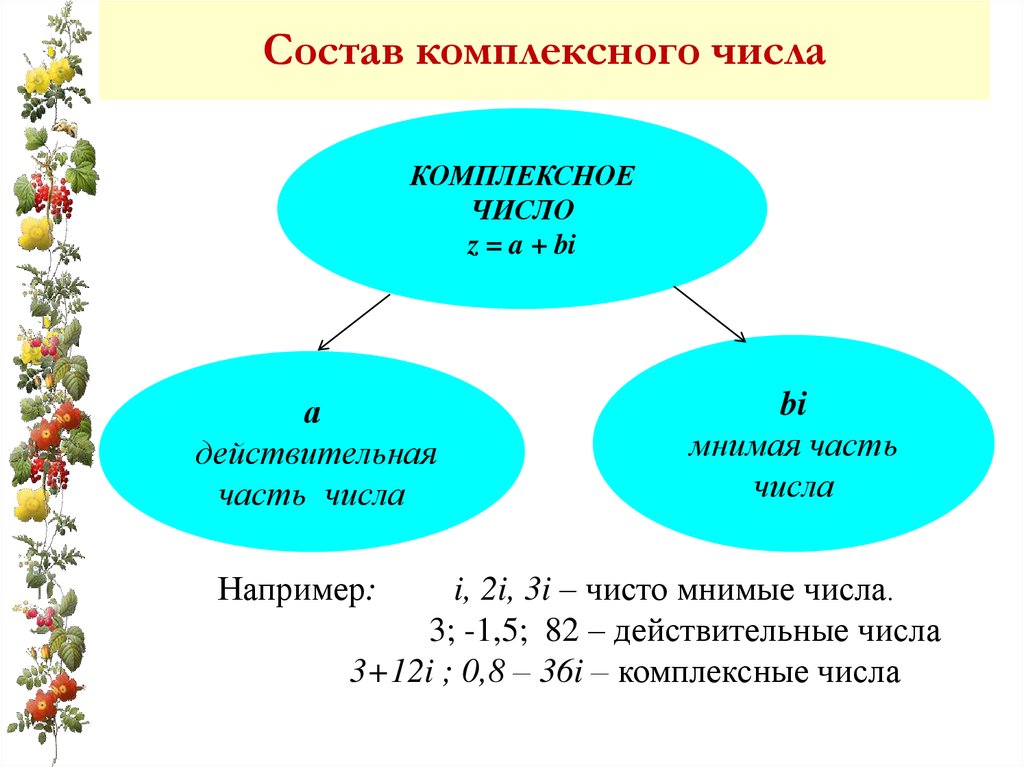
Определение комплексного числа

8. Состав комплексного числа

КОМПЛЕКСНОЕ
ЧИСЛО
z = a + bi
а
действительная
часть числа
Например:
bi
мнимая часть
числа
i, 2i, 3i – чисто мнимые числа.
3; -1,5; 82 – действительные числа
3+12i ; 0,8 – 36i – комплексные числа

9.

Равенство комплексных чисел
Например:
1+ 2i = 1+2i
или 7 - 4i = - 4i + 7
Найдите х, если
-3+i = -3+xi
5,8 – 9i = x – 9i

10.

Сопряженные числа
и
Например:
1) 5+ 2i и 5 - 2i
2) -3 - i и -3 + i

11.

Арифметические операции над КЧ:
сложение и вычитание
1)
2)
3)
Например:
1) 2i + 3i =
2) (7 - 4i ) - (i + 7 ) =
3) (-3+i ) + (5,8 – 9i ) =

12.

Арифметические операции над КЧ:
умножение и деление
4)
5)
6)

13.

Арифметические операции над КЧ:
умножение и деление

14.

Арифметические операции над КЧ:
умножение и деление

15.

Комплексные числа и квадратные
уравнения
1 ) х 12 0
2
2 ) х 4х 8 0
2
3 ) 2х 6х 9 0
2

16.

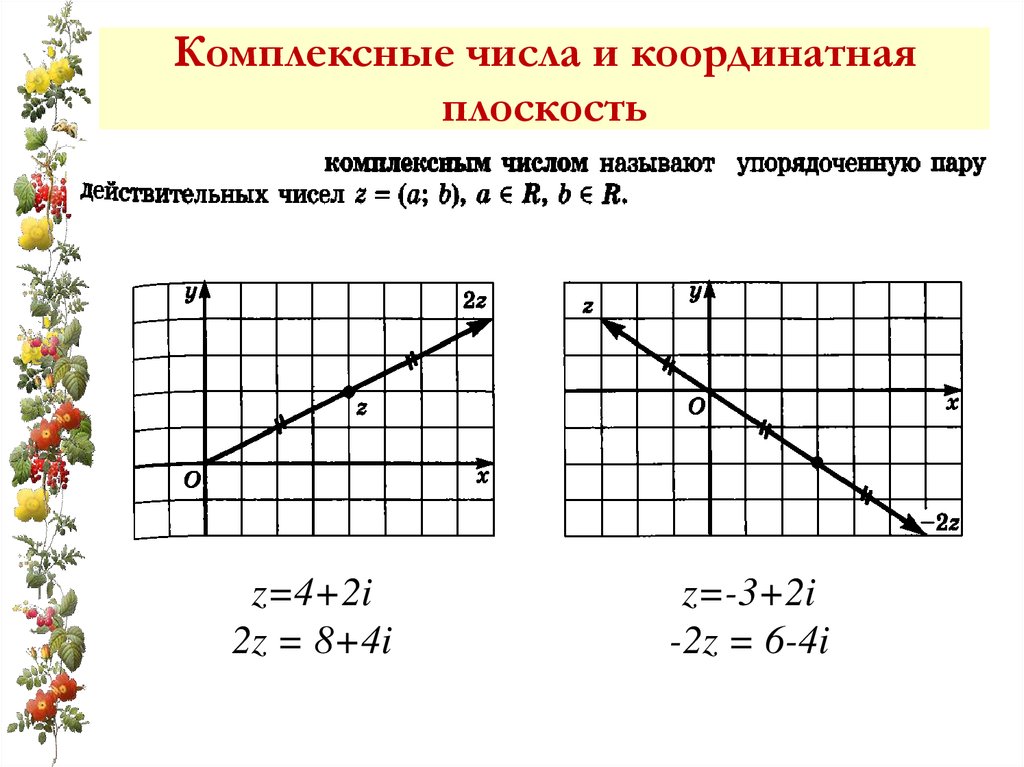
Комплексные числа и координатная
плоскость
z=4+2i
2z = 8+4i
z=-3+2i
-2z = 6-4i

17.

Модуль комплексного числа

18.

Тригонометрическая форма
комплексного числа
z x y
2
2
x
cos
z
y
sin
z

19.

20.

21.

22.

Возведение КЧ в степень
z²=(|z| (cos φ+ i sin φ))²= |z|² (cos2 φ+ i sin 2φ)
z³= z²·z=[|z| (cos φ+ i sin φ)]²·|z| (cos φ+ i sin φ)=
= |z|³ (cos3 φ+ i sin 3φ)
Формула Муавра
z z (cos i sin ) z (cos n i sin n )
n
n
n
Для любого z = r (cos φ+ i sin φ)≠0 и
любого натурального числа n

23.

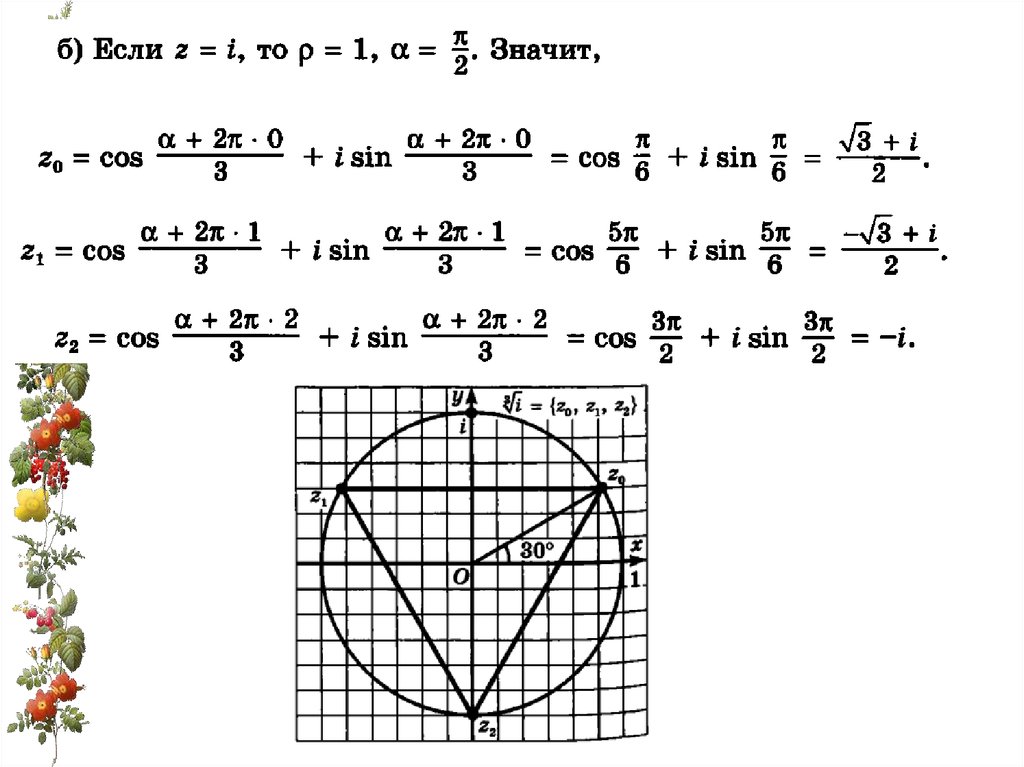
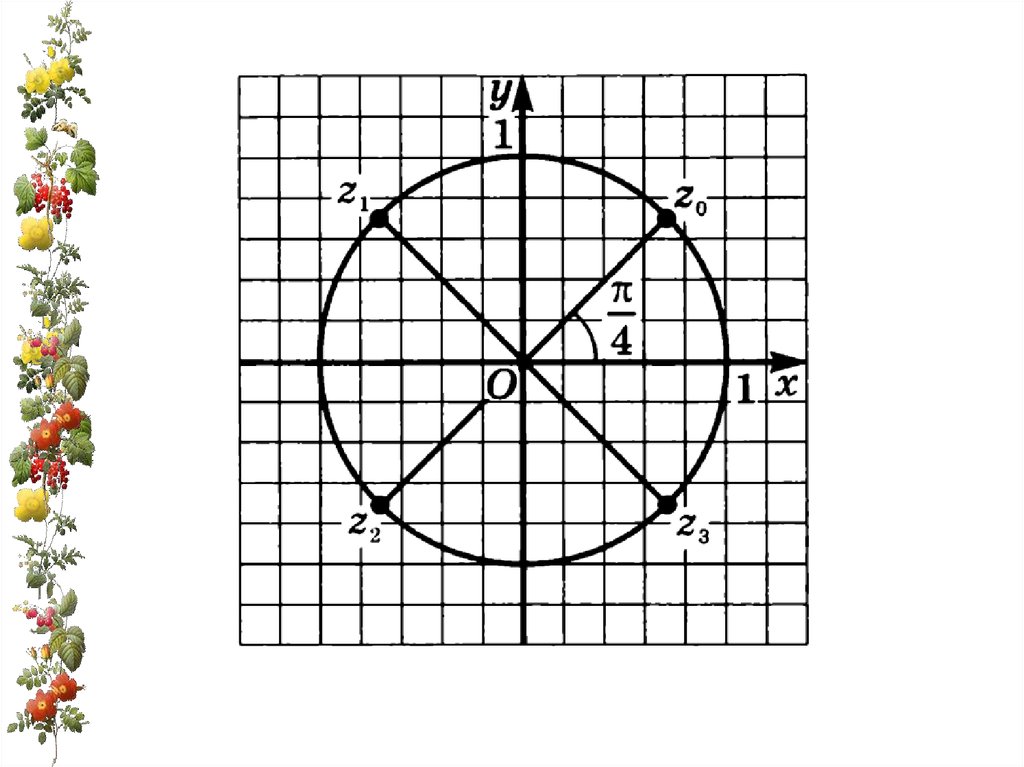
Арифметический корень из КЧ
2
k
2
k
n
z z cos
i sin
,
n
n
где k 0,1,2,..., n 1
n
z

24.

z

25.

26.

27.

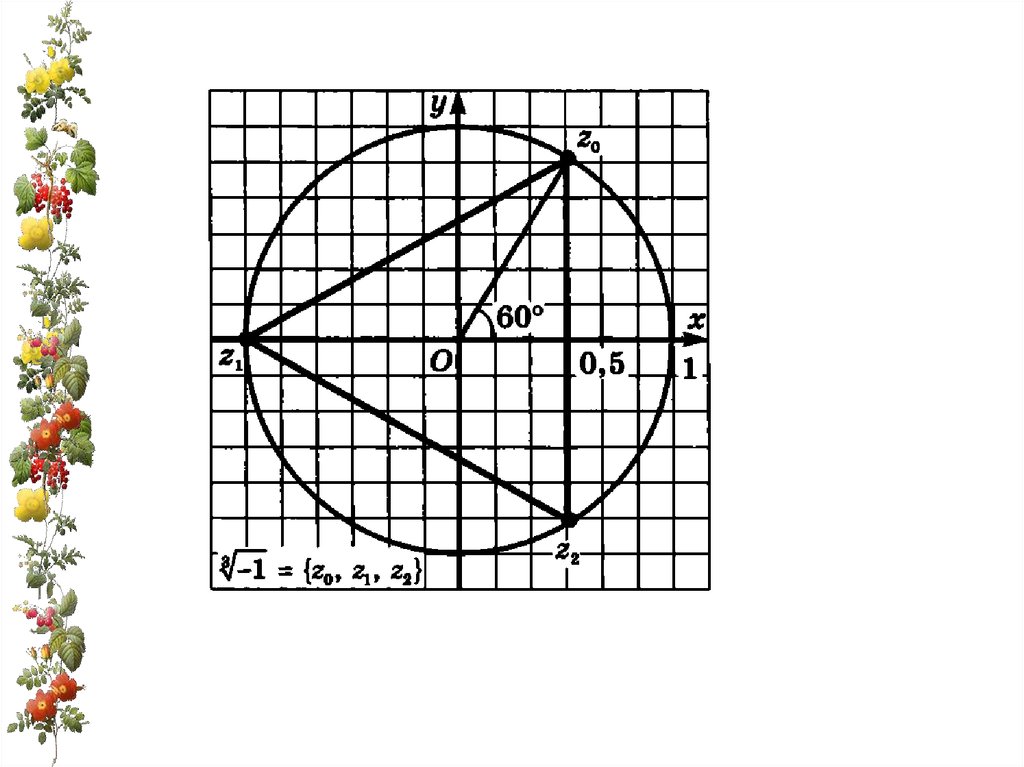
Решить уравнение:
x 3 8
r 2
x 2 (cos
2 k
3
i sin
2 k
3
),
k 0,1,2.
x1 2(cos
3
i sin
3
) 1 3 i
2
2
x 2 2(cos(
) i sin(
)) 2
3
3
3
3
4
4
x3 2(cos(
) i sin(
)) 1 3 i
3
3
3
3