Similar presentations:
Сечение единичного куба
1.
Изобразите сечение единичного куба A…D1, проходящее через вершины A, B, C1.Найдите его площадь.
Ответ.
.
2
2.
Изобразите сечение единичного куба A…D1, проходящее через середины ребер AB,BC, A1B1. Найдите его площадь.
Ответ.
2
2
.
3.
Изобразите сечение единичного куба A…D1, проходящее через вершину A исередины ребер CD, C1D1. Найдите его площадь.
Ответ.
5
.
2
4.
Изобразите сечение единичного куба A…D1, проходящее через вершину A исередины ребер BB1, DD1. Найдите его площадь.
Ответ.
.
6
2
5.
Изобразите сечение единичного куба A…D1, проходящее через вершины A, C исередину ребра С1D1. Найдите его площадь.
Решение. Сечением является равнобедренная трапеция ACEF.
Ее основания AC и EF равны
Высота FH равна
Площадь сечения равна
3 2
.
4
1
1 .
8
2,
2
.
2
6.
Изобразите сечение единичного куба A…D1, проходящее через середины ребер AB,BC, CC1. Найдите его площадь.
Ответ.
3. 3
4
7.
Изобразите сечение единичного куба A…D1, проходящее через вершину A исередины ребер BC, DD1. Найдите его площадь.
Решение. Сечением является трапеция AEFG.
Ее основания AG и EF равны соответственно
.
5
2
5
4
Для нахождения ее высоты EH рассмотрим равнобедренный треугольник AEG, в
котором AE = AG =
, EG = . Высота, опущенная на сторону
EG равна
.
5
6
Следовательно, высота EH равна
. Площадь сечения2равна
.2
14
4 3 21
105
10
16
и
8.
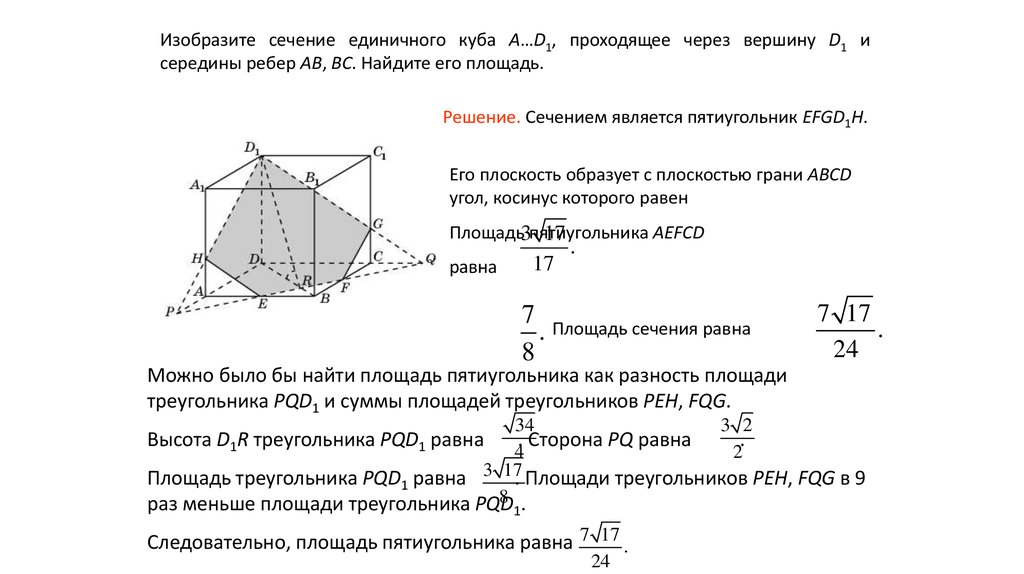
Изобразите сечение единичного куба A…D1, проходящее через вершину D1 исередины ребер AB, BC. Найдите его площадь.
Решение. Сечением является пятиугольник EFGD1H.
Его плоскость образует с плоскостью грани ABCD
угол, косинус которого равен
Площадь3пятиугольника
AEFCD
17
17
равна
.
7 Площадь сечения равна
.
8
7 17
.
24
Можно было бы найти площадь пятиугольника как разность площади
треугольника PQD1 и суммы площадей треугольников PEH, FQG.
34
3 2
. Сторона PQ равна
.
4
2
Площадь треугольника PQD1 равна 3 17. Площади треугольников PEH, FQG в 9
8 .
раз меньше площади треугольника PQD
Высота D1R треугольника PQD1 равна
1
Следовательно, площадь пятиугольника равна 7 17 .
24
9.
Изобразите сечение единичного куба A…D1, проходящее через середины ребер AB,BC, DD1. Найдите его площадь.
Ответ.
7 . 11
24
10.
Изобразите сечение тетраэдра ABCD, все ребра которого равны 1, проходящее черезсередины ребер AB, BC и CD. Найдите его площадь.
Ответ. 0,25.
11.
Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее черезсередины ребер SA, SB и SC. Найдите его площадь.
Ответ. 0,25.
12.
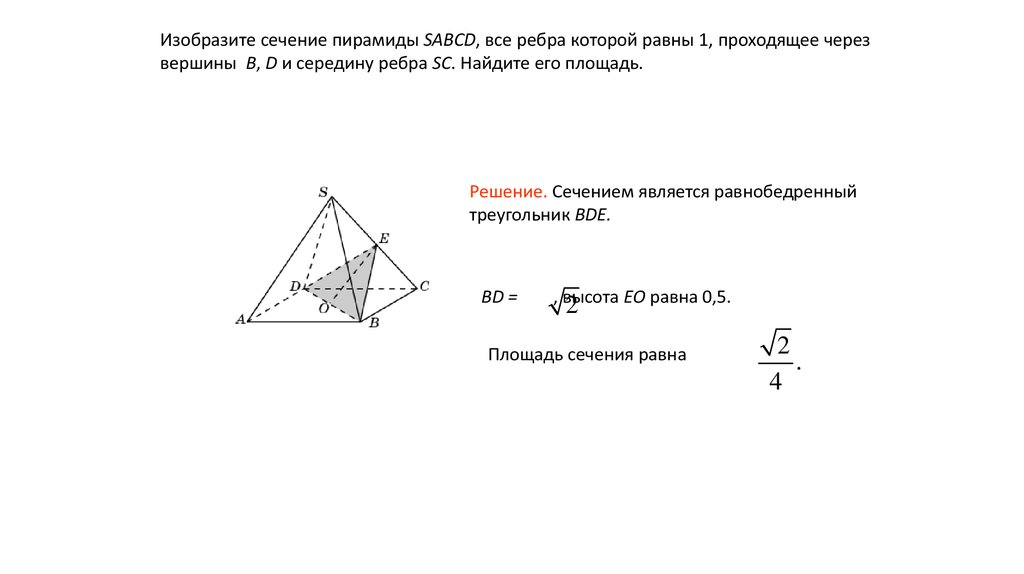
Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее черезвершины B, D и середину ребра SC. Найдите его площадь.
Решение. Сечением является равнобедренный
треугольник BDE.
BD =
, высота EO равна 0,5.
2
Площадь сечения равна
2
.
4
13.
Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее черезвершины A, B и середину ребра SC. Найдите его площадь.
Решение. Сечением является
равнобедренная трапеция ABEF.
Ее основания AB и EF равны
соответственно 1 и 0,5,
высота EH равна
Площадь сечения равна
11
.
4
3 11
.
16
14.
Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее черезсередины ребер AD, BC и SC. Найдите его площадь.
Ответ.
3 3
.
16
15.
Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее черезвершину A и середины ребер SB и SD. Найдите его площадь.
Решение. Сечением является четырехугольник
AEFG,
Его диагонали AF и GE которого
перпендикулярны и равны соответственно
10
,
3
Площадь сечения равна
2
.
4
5
.
12
16.
Изобразите сечение пирамиды SABCD, все ребра которой равны 1, проходящее черезвершину B, середину ребра SD и параллельное прямой AC. Найдите его площадь.
Решение. Сечением является четырехугольник
AEFG, диагонали BF и GE которого
перпендикулярны и равны соответственно
5
,
2
Площадь сечения равна
10
.
6
2 2
.
3
17.
Изобразите сечение пирамиды SABCDEF, стороны основания которой равны 1, абоковые ребра равны 2, проходящее через середины ребер SA, SB, SC. Найдите его
площадь.
Ответ.
3 3
.
8
18.
Изобразите сечение пирамиды SABCDEF, стороны основания которой равны 1, абоковые ребра равны 2, проходящее через вершины A, F и середину ребра SC.
Найдите его площадь.
Решение. Сечением является шестиугольник
AB1C1D1E1F.
Его площадь равна площади трапеции A1C1D1F1 минус
удвоенная площадь треугольника AA1B1.
Стороны основания трапеции равны 3 и 0,5. Высота AC1
равна
10
2
7 10
.
8
Площадь трапеции равна
Высота треугольника AA1B1, опущенная на сторону AA1, равна
Его площадь равна
10
.
6
Следовательно, площадь сечения равна
13 10
.
24
.
10
.
3
19.
Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которойравны 1, проходящее через середины ребер AA1, BB1, CC1. Найдите его площадь.
Ответ. 0,5.
20.
Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которойравны 1, проходящее через вершины B, B1 и середину ребра AC. Найдите его
площадь.
Ответ.
.
3
2
21.
Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которойравны 1, проходящее через вершины A, B и середину ребра A1C1. Найдите его
площадь.
Ответ.
3 . 19
16
22.
Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которойравны 1, проходящее через середины ребер AB, BC и CC1. Найдите его площадь.
Ответ.
3. 7
16
23.
Изобразите сечение правильной треугольной призмы ABCA1B1C1, все ребра которойравны 1, проходящее через середины ребер AB, AA1 и A1C1. Найдите его площадь.
Решение. Сечением является пятиугольник DEE1D1F.
Соединим точку F с серединой G отрезка EE1. Площадь
пятиугольника равна разности площади треугольника PQF
и суммы площадей треугольников D1E1P и DEQ.
Сторона PQ треугольника PQF равна
Высота FG равна
Площади треугольников D1E1P и DEQ равны
Площадь сечения равна
3 15
.
16
. Его площадь
равна
3
2
15
.
32
.
5
15
.
4
24.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через вершины A, C и C1. Найдите его площадь.
Ответ.
.
3
25.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через вершины A, D и D1. Найдите его площадь.
Ответ. 2.
26.
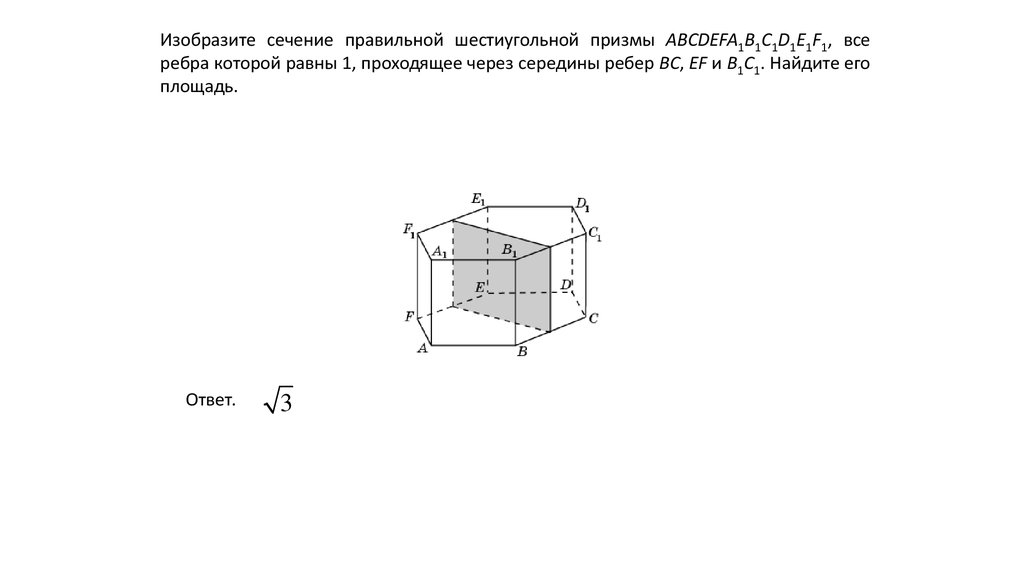
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через середины ребер BC, EF и B1C1. Найдите его
площадь.
Ответ.
.
3
27.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через середины ребер AB, BC и A1B1. Найдите
его площадь.
Ответ.
.
3
2
28.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через середины ребер AB, CD и A1B1. Найдите
его площадь.
Ответ. 1,5.
29.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через вершины D, D1 и середину ребра EF.
Найдите его площадь.
Ответ.
.
7
2
30.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через вершины A, A1 и середину ребра CD.
Найдите его площадь.
Ответ.
.
13
2
31.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через вершины A, C и D1. Найдите его площадь.
Ответ.
.
6
32.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через вершины A, D и C1. Найдите его площадь.
Ответ.
3. 7
4
33.
Изобразите сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, всеребра которой равны 1, проходящее через вершины A, B и D1. Найдите его площадь.
Решение. Сечением является шестиугольник.
Его плоскость образует угол с плоскостью ABC,
косинус которого равен
Площадь основания
призмы равна
3
.
Площадь сечения
равна 3.
2
3 3
.
2






























 mathematics
mathematics








