Similar presentations:
Математические предложения
1.
Математические предложения2.
В языке связи между объектами и ихсвойствами выражаются с помощью
предложений, которые образуются из
понятий.
«В равностороннем треугольнике все
углы равны»
«Число 28 делится на 7»
3.
Каждое математическое предложениехарактеризуется содержанием и логической
структурой.
В математике по структуре различают
элементарные и составные предложения.
-элементарное предложение:
«Число 28 делится на 7»
-составные предложения:
«Число 28 четное и делится на 7»,
«Число х меньше или равно 8»,
«Если треугольник равнобедренный, то углы в
нем при основании равны»,
«Число 14 не делится на 4»
4.
Составные образуются из элементарныхс помощью слов «и», «или», частицы
«не» и некоторых других. Эти слова в
математике называют логическими
связками.
Выявить логическую структуру
составного предложения – значит
установить:
из каких элементарных предложений
образовано данное составное
с помощью каких логических связок
оно образовано.
5.
составные предложения:«Число 28 четное и делится на 7»
«Число х меньше или равно 8»
«Если треугольник равнобедренный, то
углы в нем при основании равны»
«Число 14 не делится на 4»
6. Приведите примеры предложений, имеющих структуру:
АиВА или В
Если А, то В
7.
Среди суждений, устанавливающихразличные отношения между
математическими понятиями,
выделяют высказывания и
высказывательные формы.
8.
Высказыванием называетсяпредложение, относительно которого
имеет смысл вопрос, истинно оно
или ложно.
«число 6 четное» - истинное
высказывание
«2+2=5» - ложное высказывание
Если высказывание элементарное, то его
значение истинности определяют по
содержанию, опираясь на известные
знания.
9.
Высказывание вида «А и В» истинно,если истинны оба высказывания А и
В.
Если же хотя бы одно из них ложно, то
высказывание «А и В» ложно
10. Если высказывание составное, то считают, что:
1)Высказывание вида «А и В»
истинно, если истинны оба
высказывания А и В.
Если же хотя бы одно из них ложно,
то высказывание «А и В» ложно.
11.
Например:- высказывание «6 больше 3 и меньше 7»
истинно, т.к. истинно каждое
высказывание
- высказывание «число 102 четное и
делится на 9» ложно, т.к. А – истинно,
но В – ложно.
12.
2) высказывание вида «А или В»истинно, если истинно хотя бы одно
из высказываний. Ложно тогда, когда
ложны оба высказывания.
13.
Например,- высказывание «число 102 четное или
делится на 3»: истинны оба высказывания
«число 102 четное» и «число 102 делится
на 3», следовательно и истинно и само
составное высказывание.
- высказывание «число 3 меньше либо
равно 7» имеет форму «А или В» и оно
истинно, т.к. истинно высказывание А (3
меньше 7), а высказывание В ложно (3
равно 7).
- высказывание «число 5 меньше либо
равно 3» ложно, т.к ложны обе части
высказывания.
14.
Отрицание высказывания Аназывается высказывание А,
которое истинно, если высказывание
А ложно, и ложно, когда А истинно.
15.
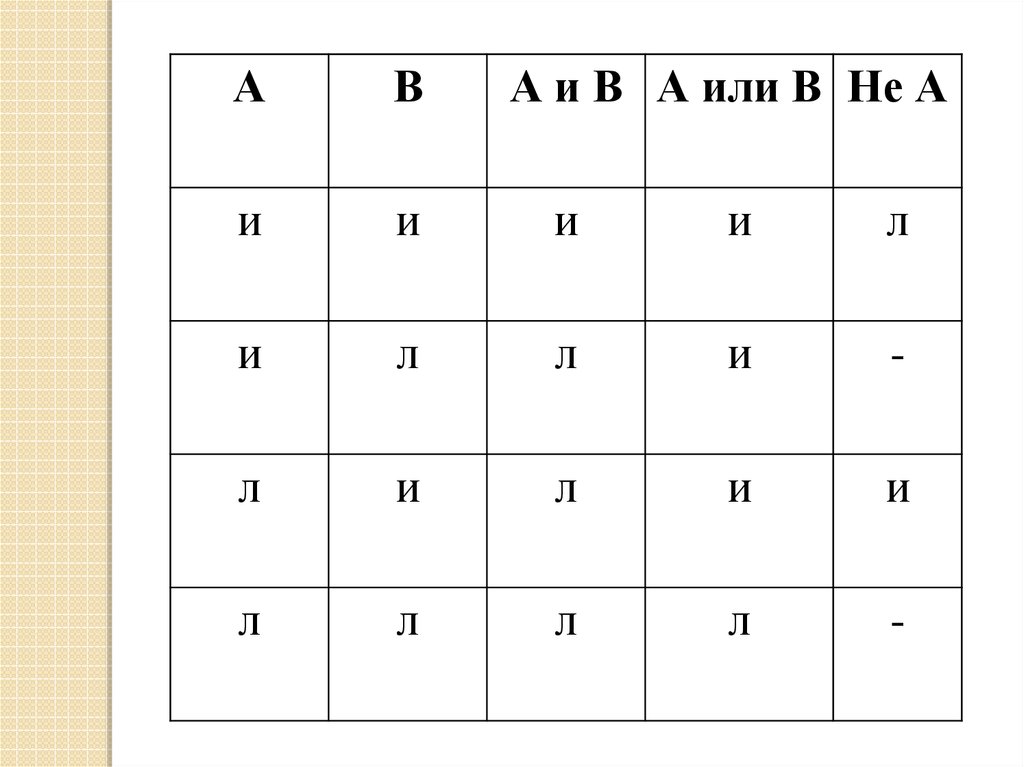
АВ
А и В А или В Не А
и
и
и
и
л
и
л
л
и
-
л
и
л
и
и
л
л
л
л
-
16.
В математике часто встречаютсяпредложения, содержащие одну или
несколько переменных. Например,
х+3=5, х-у=4. Эти предложения не
являются высказываниями, т.к.
относительно таких предложений
нельзя сказать, истинны они или
ложны.
Предложения такого вида называют
высказывательными формами.
17.
Высказывательная форма – этопредложение с одной или
несколькими переменными, которое
обращается в высказывание при
подстановке в него конкретных
значений переменных.
18.
Понятие высказывательная форма можнорассматривать как обобщение известных
понятий: уравнения с одной переменной,
с двумя и т.д. переменными, неравенства с
переменными и т.д.
Если высказывательная форма – уравнение
(или неравенство), то, чтобы дать ответ на
этот вопрос, надо уравнение (или
неравенство) решить.
Например, при каком значении переменной
х высказывательная форма 3х – 4 = 5
обращается в истинное высказывание?
19. Отношения следования и равносильности между предложениями.
Любое рассуждение не обходится безслов «следовательно», «из данного
предложения следует», «отсюда
вытекает».
20.
Возьмем два предложения:А – «х кратно 4» и В – «х кратно 2».
Они связаны между собой:
любое число, кратное 4 кратно 2,
или иначе: из того, что число кратно 4,
следует, что кратно 2.
21.
Говорят, что из предложения А следуетпредложение В, если всякий раз,
когда истинно предложение А,
истинно и предложение В.
Предложение «Из А следует В» можно
записать, используя символ
22.
Запись читают по разному:А) из А следует В
Б) В следует из А
В) если А, то В
Г) есть А, следовательно, есть В
Д) всякое А есть В.
Прочитайте по-разному:
«х кратно 4, следовательно, х кратно 2»
23.
А- «треугольник равнобедренный»В- «углы при основании треугольника
равны».
24.
Если из предложения А следуетпредложение В, а из предложения В
следует предложение А, то говорят,
что предложения А и В
равносильны.
Предложение «А равносильно В»
записывают: А В.
читают:
А) А равносильно В
Б) А тогда и только тогда , когда В
В) А если и только, если В.
25. Задание:
Вставьте «и», «или», так, чтобыпредложения были истинными:
1) а*в=0 равносильно а=0… в=0
а*в не равно 0 равносильно
а не равно 0… в не равно 0.
2)
























 mathematics
mathematics








