Принцип Ле-Шателье-Брауна. Термодинамика необратимых процессов. Циклы энергетических установок. (Лекция 6)

1.

ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА
ПРИНЦИП ЛЕ-ШАТЕЛЬЕ - БРАУНА,
ТЕРМОДИНАМИКА НЕОБРАТИМЫХ
ПРОЦЕССОВ,
ЦИКЛЫ ЭНЕРГЕТИЧЕСКИХ
УСТАНОВОК

2. Возрастание энтропии изолированной системы происходит до тех пор, пока в ней не затухают все необратимые процессы. В этом случае энтропия

Принцип Ле-Шателье - Брауна
Возрастание энтропии изолированной системы происходит до тех
пор, пока в ней не затухают все необратимые процессы. В этом
случае энтропия достигает максимального значения.
Следовательно, условие устойчивости состояния
термодинамической системы можно сформулировать как:
Если энтропия адиабатически изолированной термодинамической
системы принимает максимальное значение, то ее состояние
термодинамически устойчиво.
При устойчивом термодинамическом равновесии энтропия
адиабатически изолированной системы имеет экстремум: S = S ,
где S - энтропия системы в состоянии термодинамического
равновесия. Следовательно, в состоянии устойчивого равновесия
первая вариация энтропии изолированной термодинамической
системы S = 0, а вторая ее вариация - S2 < 0. Условие
равенства нулю первой вариации энтропии дает необходимое
условие равновесия изолированной системы, а неравенство
S2 < 0 - достаточное условие устойчивости равновесного
состояния

3.

Принцип Ле-Шателье - Брауна
Реакцию системы на внешние воздействия можно качественно
определить на основе принципа Ле-Шателье - Брауна,
предложенного в 1884 году французским химиком Анри Луи ЛеШателье (1850 - 1936) и обоснованного в 1887 году немецким
физиком Карлом Фердинандом Брауном (1850 - 1918):
Внешние воздействия, выводящие термодинамическую
систему из состояния устойчивого равновесия, вызывают в ней
протекание процессов, которые уменьшают влияние этих
внешних возмущений.
Этот принцип позволяет предсказать направление протекания
процессов в термодинамической системе, которая выводится из
состояния устойчивого равновесия внешними воздействиями.
Например, имеется смесь льда и воды, находящаяся в состоянии
устойчивого равновесия. Если этой смеси сообщить некоторое
количество теплоты, то лед начнет таять, что будет
препятствовать повышению температуры смеси. То есть,
протекающий в системе процесс таяния льда будет ослаблять
изменения, вызываемые подводом теплоты

4. Пример: Один моль идеального газа находится в эластичной оболочке, с внешней стороны которой действует постоянное давление. Покажем, что п

Принцип Ле-Шателье - Брауна
Пример: Один моль идеального газа находится в эластичной
оболочке, с внешней стороны которой действует постоянное
давление. Покажем, что при подводе к этому газу некоторого
количества теплоты Q произойдет его расширение,
приводящее, в соответствии с принципом Ле-Шателье - Брауна,
к уменьшению изменения его температуры T по сравнению с
изменением температуры T0, которое имело бы место при
неизменном объеме газа: T < T0
Для одного моля идеального газа в случае изобарического
процесса:
Q
T
CP
Для изохорического процесса:
Q
T0
CV

5.

Принцип Ле-Шателье - Брауна
Отсюда имеем, имеем
CV
T
T0
CP
Так как CP > CV, то T < T0. Из этого следует, что в
рассматриваемой термодинамической системе при внешнем
воздействии (подводе теплоты) возникает процесс (расширение
газа), приводящий к уменьшению влияния внешнего
возмущения: изменение температуры газа меньше, чем, если
бы расширение не возникало

6.

Термодинамика необратимых процессов
Для описания необратимых процессов можно воспользоваться
гипотезой локального равновесия: внутри малого объема среды
выполняется основное уравнение термодинамики равновесных
процессов. Если в качестве параметров состояния ввести
локальную плотность внутренней энергии
u (r , t )
приходящуюся на единицу массы среды, и удельный объем
v(r , t )
где
- (r , t )
1
(r , t )
локальная плотность среды

7.

Термодинамика необратимых процессов
Для точки среды с координатами {x,y,z} в момент времени t
можно записать уравнение в удельных величинах
Tds du Pdv
Тогда внутренняя энергия всей системы определяется с
помощью выражения
U (r , t )u (r , t )dV
V
а ее энтропия S соответственно может быть найдена по формуле
S (r , t ) s (r , t )dV
V
Совместное применение данных уравнений позволяет построить
феноменологическую термодинамику необратимых процессов,
опирающуюся на использование полученных из опыта
соотношений между параметрами, описывающими
термодинамические процессы.

8.

Термодинамика необратимых процессов
Ключевое значение в термодинамике необратимых
процессов имеет величина, численно равная скорости
увеличения энтропии в единице объема:
d ( s )
S
dt
Эта величина
представляет собой производство
энтропии для единичного объема адиабатически
изолированной системы. Она описывает количество
энтропии, которая возникает в единичном объеме
термодинамической системы за единицу времени при
протекании в ней необратимых термодинамических
процессов

9.

Термодинамика необратимых процессов
Если в качестве термодинамических параметров системы
выступают N величин a(r,t), то можно записать:
d ( s ) N ( s ) dai
S
dt
dt
i 1 ai
( s )
Xi
ai
dai
ji
dt
термодинамические силы
плотности термодинамических потоков
N
Следовательно
S X i ji
i 1

10. В случае небольших отклонений от равновесного состояния между термодинамическими потоками ji и термодинамическими силами Xk может быть уст

Термодинамика необратимых процессов
В случае небольших отклонений от равновесного состояния
между термодинамическими потоками ji и
термодинамическими силами Xk может быть установлена
линейная зависимость
N
ji Lik X k
k 1
Это соответствует наиболее простому случаю
термодинамики линейных необратимых процессов.
Таким образом, для линейных необратимых процессов
производство энтропии определяется выражением
S
N
L
k ,i 1
ik
Xi Xk
или
S
N
L
k ,i 1
ik
1
ji jk

11.

Термодинамика необратимых процессов
Коэффициенты Lik называются кинетическими
коэффициентами, и они характеризуют интенсивность
явлений переноса. В 1931 году американский физик и
химик Ларс Онсагер (1903 - 1976) установил, что для
кинетических коэффициентов выполняется условие
(соотношением взаимности Онсагера):
Lik Lki
указывающее на симметрию матрицы кинетических
коэффициентов.
Одним из принципов термодинамики линейных необратимых
процессов является предложенный в 1947 году бельгийским
физико-химиком Ильей Романовичем Пригожиным принцип
минимума производства энтропии: Стационарные
необратимые процессы протекают таким образом, чтобы
производство энтропии было минимальным.

12.

Термодинамика необратимых процессов
Принцип минимума производства энтропии позволяет
установить критерий отбора реализующихся в природе
необратимых процессов от реально не наблюдающихся, и,
таким образом, выбрать из возможных процессов реально
существующие.
Необходимость выполнения указанного принципа приводит к
тому, что при протекании в среде необратимых стационарных
процессов возникают динамические структуры, названные
Пригожиным диссипативными структурами, что уменьшает
производство энтропии. Примером таких структур могут
служить ячейки Бенара - регулярные динамические структуры,
возникающие в тонком слое нагреваемой снизу жидкости, и
колебательные химические реакции Б.П. Белоусова, при
которых происходят периодические изменения концентрации
реагирующих веществ.

13.

Термодинамика необратимых процессов
Пример возникновения
пространственной
структуры: «Ячейки
Бенара».
Ячейки Бенара возникают при критической разности
температур, возникающей между верхним и нижним
слоями жидкости при ее нагревании (жидкость
находится в кювете).

14.

Термодинамика необратимых процессов
Примером временной структуры является реакция
Белоусова – Жаботинского.
Реакция Белоусова – Жаботинского наблюдается в
реакционной смеси, состоящей из бромата калия (KBr),
броммалоновой кислоты, сульфата церия (Се).
Смесь нужно растворить либо в лимонной, либо в
серной кислоте. Окраска раствора через 4 мин
изменяется с синего на красный (и наоборот).
Это происходит в связи с восстановлением ионов
церия:
Се+4 Се+3
Чередование
окраски
раствора
является
самоорганизованным, развивающимся во времени.

15.

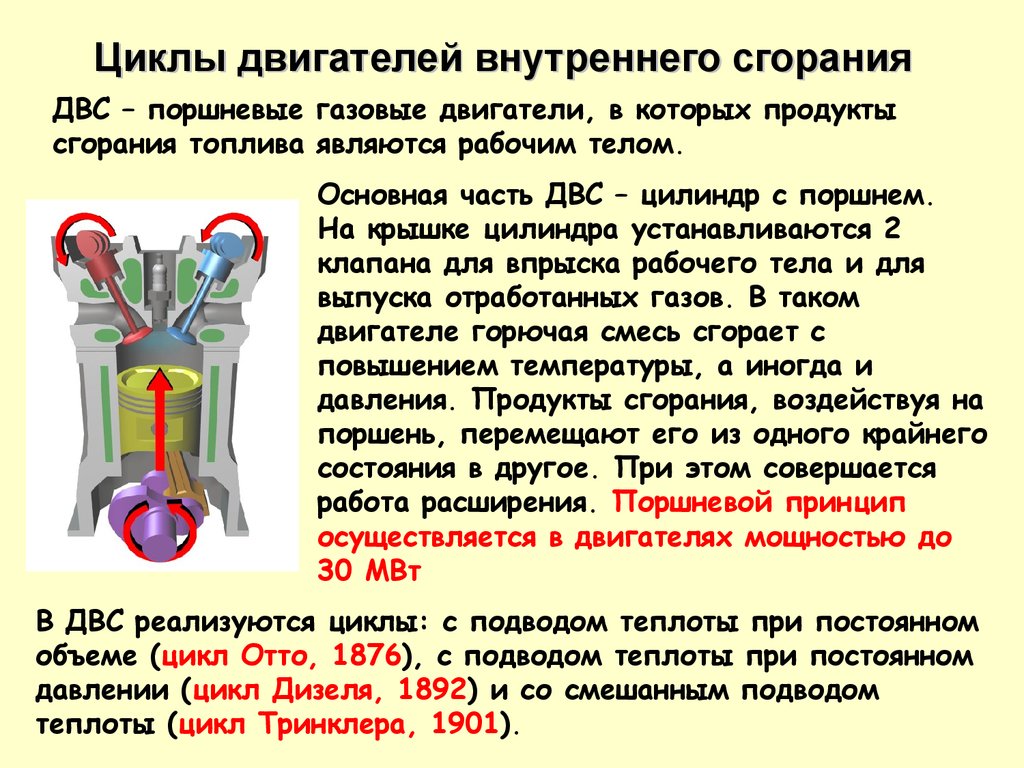
Циклы двигателей внутреннего сгорания
ДВС – поршневые газовые двигатели, в которых продукты
сгорания топлива являются рабочим телом.
Основная часть ДВС – цилиндр с поршнем.
На крышке цилиндра устанавливаются 2
клапана для впрыска рабочего тела и для
выпуска отработанных газов. В таком
двигателе горючая смесь сгорает с
повышением температуры, а иногда и
давления. Продукты сгорания, воздействуя на
поршень, перемещают его из одного крайнего
состояния в другое. При этом совершается
работа расширения. Поршневой принцип
осуществляется в двигателях мощностью до
30 МВт
В ДВС реализуются циклы: с подводом теплоты при постоянном
объеме (цикл Отто, 1876), с подводом теплоты при постоянном
давлении (цикл Дизеля, 1892) и со смешанным подводом
теплоты (цикл Тринклера, 1901).

16.

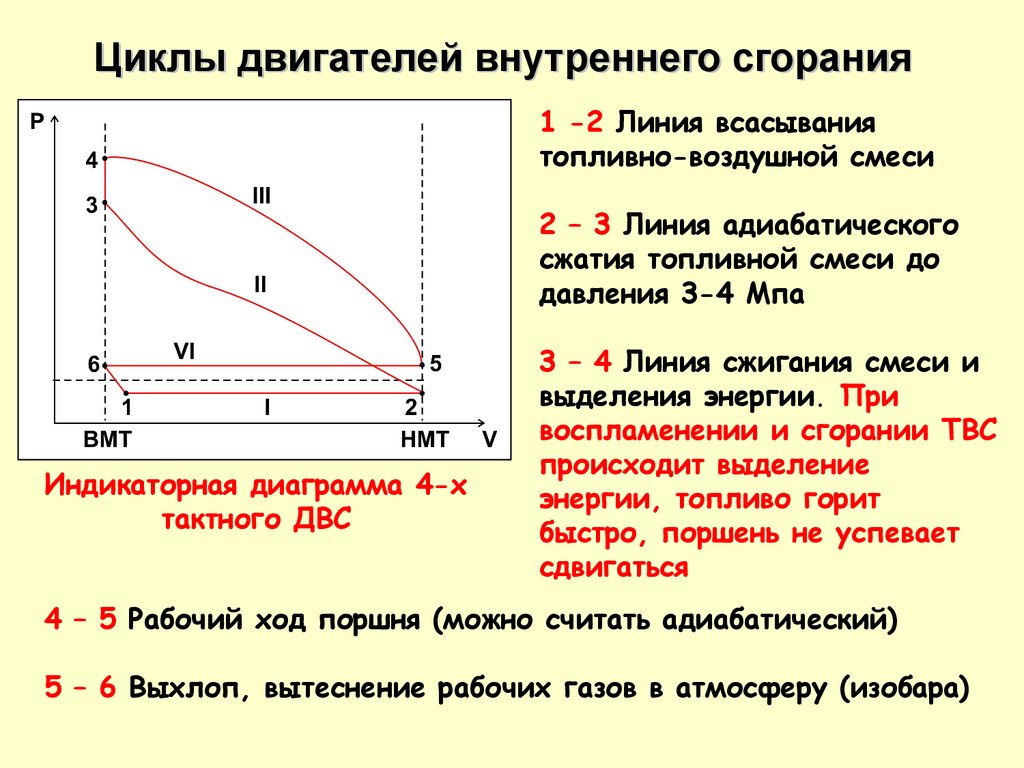
Циклы двигателей внутреннего сгорания
1 -2 Линия всасывания
топливно-воздушной смеси
2 – 3 Линия адиабатического
сжатия топливной смеси до
давления 3-4 Мпа
Индикаторная диаграмма 4-х
тактного ДВС
3 – 4 Линия сжигания смеси и
выделения энергии. При
воспламенении и сгорании ТВС
происходит выделение
энергии, топливо горит
быстро, поршень не успевает
сдвигаться
4 – 5 Рабочий ход поршня (можно считать адиабатический)
5 – 6 Выхлоп, вытеснение рабочих газов в атмосферу (изобара)

17.

Циклы двигателей внутреннего сгорания
Для термодинамического анализа рабочий процесс
двигателя, как правило, заменяют идеальным
термодинамическим циклом, при этом делают
допущения:
1)Процесс горения смеси заменяют процессом
подвода тепла извне
2)Процесс выхлопа заменяют отводом тепла во
внешнюю среду
3)Потерями на теплообмен и трение пренебрегают
4)Считается, что рабочее тело не обновляется, т.е.
система замкнутая

18.

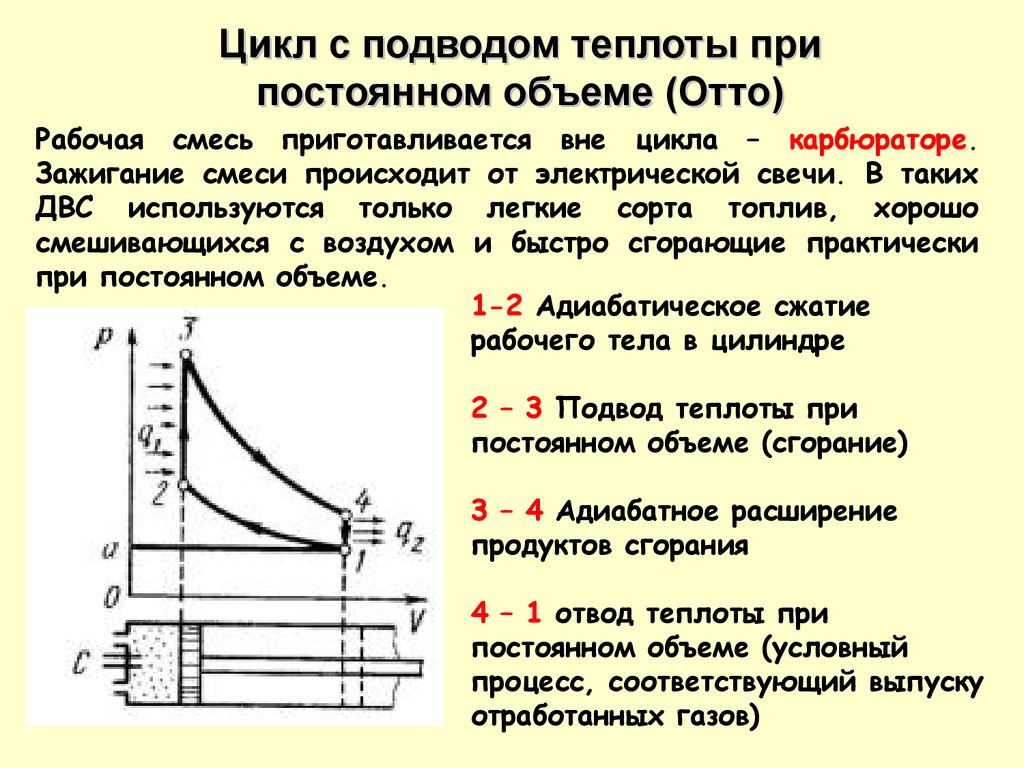
Цикл с подводом теплоты при
постоянном объеме (Отто)
Рабочая смесь приготавливается вне цикла – карбюраторе.
Зажигание смеси происходит от электрической свечи. В таких
ДВС используются только легкие сорта топлив, хорошо
смешивающихся с воздухом и быстро сгорающие практически
при постоянном объеме.
1-2 Адиабатическое сжатие
рабочего тела в цилиндре
2 – 3 Подвод теплоты при
постоянном объеме (сгорание)
3 – 4 Адиабатное расширение
продуктов сгорания
4 – 1 отвод теплоты при
постоянном объеме (условный
процесс, соответствующий выпуску
отработанных газов)

19.

Цикл с подводом теплоты при
постоянном объеме (Отто)
Чтобы не делать цилиндр очень длинным, а ход поршня большим,
расширение продуктов сгорания в ДВС идет не до атмосферного
p1, а до более высокого p4, а затем открывают выпускной клапан.
Избыточное давление p4 – p1 при этом теряется бесполезно.
Степень сжатия двигателя - отношение
цилиндра к объему камеры сгорания.
полного
объема
V1
V2
Степень сжатия двигателя – основной параметр, определяющий
термический КПД цикла.
Термический КПД цикла ДВС увеличивается с ростом степени
сжатия.

20.

Цикл с подводом теплоты при
постоянном объеме (Отто)
Например, для цикла со сгоранием при V = const, при
постоянной теплоемкости:
CV (T4 T1 )
q2
(T4 / T1 1)T1
T 1
1
1
q1
CV (T3 T2 )
(T3 / T2 1)T2
При одинаковых показателях адиабаты k процессов сжатия и
расширения можно записать:
T3 T2
k 1
T4 T1
Тогда:
T3 T4
k 1
T2 T1
( k 1 1)
1
T 1 k 1
1
( 1) k 1
k 1
В карбюраторном двигателе максимальная степень сжатия
ограничивается самовоспламенением ТВС и не превышает 9-10.
В дизелях, в которых поршень сжимает воздух, ≈ 18, что
позволяет существенно повысить КПД цикла.

21.

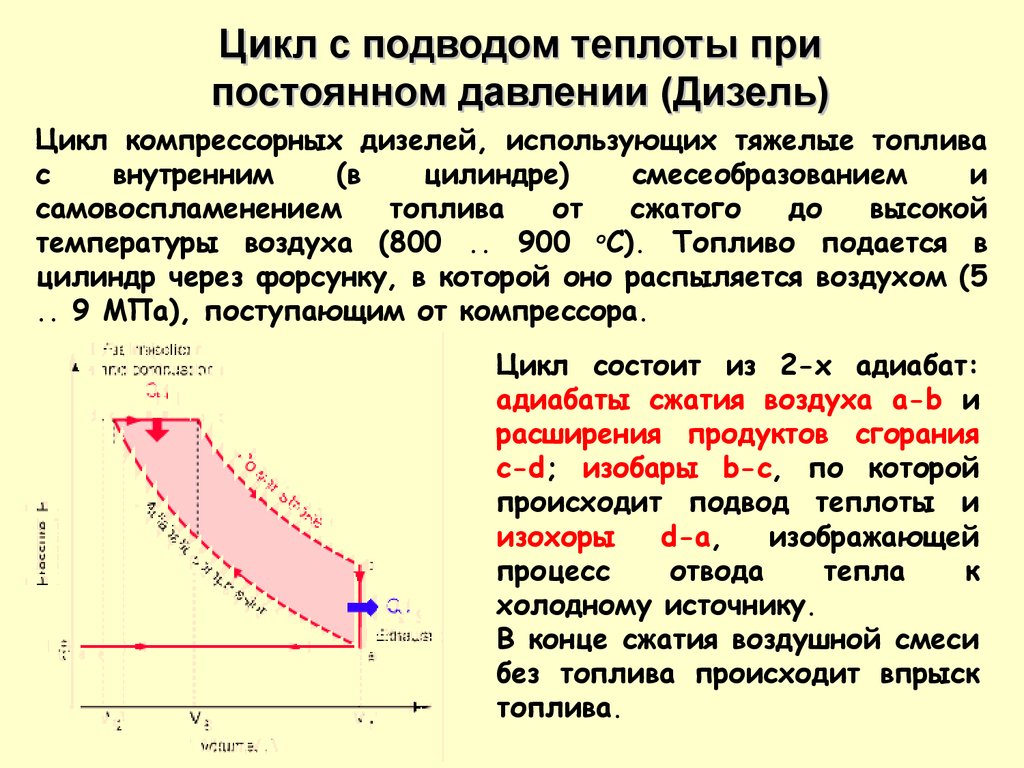
Цикл с подводом теплоты при
постоянном давлении (Дизель)
Цикл компрессорных дизелей, использующих тяжелые топлива
с
внутренним
(в
цилиндре)
смесеобразованием
и
самовоспламенением
топлива
от
сжатого
до
высокой
температуры воздуха (800 .. 900 оС). Топливо подается в
цилиндр через форсунку, в которой оно распыляется воздухом (5
.. 9 МПа), поступающим от компрессора.
Цикл состоит из 2-х адиабат:
адиабаты сжатия воздуха a-b и
расширения продуктов сгорания
c-d; изобары b-c, по которой
происходит подвод теплоты и
изохоры
d-a,
изображающей
процесс
отвода
тепла
к
холодному источнику.
В конце сжатия воздушной смеси
без топлива происходит впрыск
топлива.

22.

Цикл с подводом теплоты при
постоянном давлении (Дизель)
Впрыск происходит достаточно долговременно, так что с
отводом поршня от ВМТ давление остается постоянным из-за
постоянного поступления топлива и его сгорания.
Ведем степень предварительного расширения:
q2
T 1
q1
q1 C P (T3 T2 )
V3
V2
q2 CV (T4 T1 )
CV (T4 T1 )
T4 T1
T 1
1
C P (T3 T2 )
k (T3 T2 )

23.

Цикл с подводом теплоты при
постоянном давлении (Дизель)
Для изобары b-c имеем:
PV3 RT3
Для адиабаты c-d:
Аналогично для a-b:
Отсюда:
V3 T3
T3
T2
V2 T2
PV2 RT2
V
T3V3k 1 T4V1k 1 T4 T3 3
V1
k 1
2 2
TV
k 1
1 1
TV
k 1
V2
T1 T2
V1
T3 V1
T1
V2
( k 1)
V
T3 1
V3
k 1
T3 1
k 1
( k 1)
V1
T2
V2
( k 1)

24.

Цикл с подводом теплоты при
постоянном давлении (Дизель)
T3 (V1 / V3 ) ( k 1) (T3 / k 1 )
(T3 / k 1 ) (T3 / k 1 )
T 1
1
k[T3 (T3 / )]
k[T3 (T3 / )]
(1 / k 1 ) (1 / k 1 )
1
k[1 (1 / )]
где = V1/V3 – степень адиабатного расширения
С учетом = V1/V2, = V1/V3, ρ = V3/V2, то
V1 V1 V3
V2 V3 V2
КПД цикла Дизеля:
1 k 1
T 1 k 1
1
k