Similar presentations:
Медицинская информатика - важная часть в изучении медицины
1. Медицинская информатика-важная часть в изучении медицины
Медицинская информатикаважная часть в изучениимедицины
2.
Медицинская информатика — это научная дисциплина, занимающаяся исследованиемпроцессов получения, передачи, обработки, хранения, распространения, представления
информации с использованием информационной техники и технологии в медицине и
здравоохранении.
Предметом изучения медицинской информатики при этом будут являться информационные
процессы, сопряженные с медико-биологическими, клиническими и профилактическими
проблемами.
Объектом изучения МИ являются информационные технологии, реализуемые в
здравоохранении.
Информационные технологии — это преимущественно компьютеризированные способы
выработки, хранения, передачи и использования информации.
3.
Роль медицинской информатики в научно-практическом обосновании и использованиисовременных технологий заключается в нахождении новых решений на стыке формального
и логического подходов с эмпирическим описательным характером медицины. Основой
основ при работе с информацией является мышление и логический анализ. Именно они
лежат в основе клинического диагноза - фиксированной на информационном носителе
заключения врача о локализации, характере и стадию заболевания, которое обосновывает
оптимальный выбор лечебной тактики (управляющей действия) в пределах имеющихся
медицинских ресурсов.
4. Обработка информации в сложных системах
Входные контролируемыефакторы
Неконтролируемые
факторы
СЛОЖНАЯ СТОХАСТИЧЕСКАЯ
СИСТЕМА
Выходные контролируемые
факторы
Случайные факторы
5.
Изучаемые в медицине объекты являются сложными стохастическими системами функционирующими при воздействии на нихмножества входных факторов. Часть факторов Х1, Х2, …, Хk является контролируемыми. Другая часть относится к группе
случайных факторов, оказывающих воздействие на систему.
Состояние системы характеризуется множеством выходных параметров Y1, Y2,…, Yl , которые также измеряются количественно
или в баллах и представляют собой случайные величины, следующие какому-либо закону распределения с соответствующими
числовыми характеристиками. В силу того, что неконтролируемые и случайные факторы для каждого объекта наблюдения
принимают различные случайные значения, выходные параметры, характеризующие состояние и функционирование сложной
стохастической (вероятностной) системы, являются случайными величинами, для исследования которых следует применять
методы теории вероятности и математической статистики.
Количество входных контролируемых факторов и выходных параметров, описывающих объект исследования,
определяется в зависимости от цели и задачи исследования.Так, например, для исследования связи между факторами
тяжести состояния и факторами и параметрами, характеризующими эффективность лечения пострадавших с сочетанной
механической травмой при ведущем повреждении головы, в качестве входных контролируемых факторов целесообразно
иметь:
X1 – возраст, лет;
X2 –время доставки, ч;
X3 – частота пульса, уд/мин;
X4 – артериальное давление систолическое, мм.рт.ст.;
X5 – тип дыхания, в баллах: 1- нормальное, 2- частое, 3- патологическое;
Выходными параметрами могут быть:
Y1 – возникновение осложнений, в баллах: 0 – нет, 1 – есть;
Y2 – срок лечения, дней;
Y3 –исход лечения, в баллах: 0 – выжил, 1 – умер.
6.
Для определения методов статистического анализа необходимо знать характер, распределенияи числовые характеристики всех переменных, входящих в матрицу наблюдений. Наилучшие
результаты многомерного статистического анализа данных медико-биологических
исследований получают, когда распределения входных контролируемых факторов и выходных
параметров нормальное или близкое к нему. Основными задачами статистического описания
переменных являются:
определение числовых характеристик переменных и оценка их точности и надежности;
определение статистических рядов распределения переменных и оценки их соответствия
теоретическим законам распределения;
оценка зависимости различия показателей в независимых и связанных выборках
По числовым характеристикам, таким, как среднее арифметическое значение,
среднее квадратичное отклонение, средняя квадратичная ошибка среднего значения
определяют доверительные интервалы, решаются задачи нормирования и
оценивается значимость различий показателей в различных условиях.
Статистический ряд распределения дает представление о виде распределения
показателя в диапазоне полученных наблюдений и является основой для оценки его
соответствия с тем или иным теоретическим законом распределения. Оценка
значимости различия показателей в независимых и связанных выборках – одна из
основных задач решаемых исследователями при сравнении методов профилактики,
лечения различных заболеваний, состояния работоспособности сотрудников
трудовых коллективов в различных условиях и в других подобных ситуациях. (устно)
7.
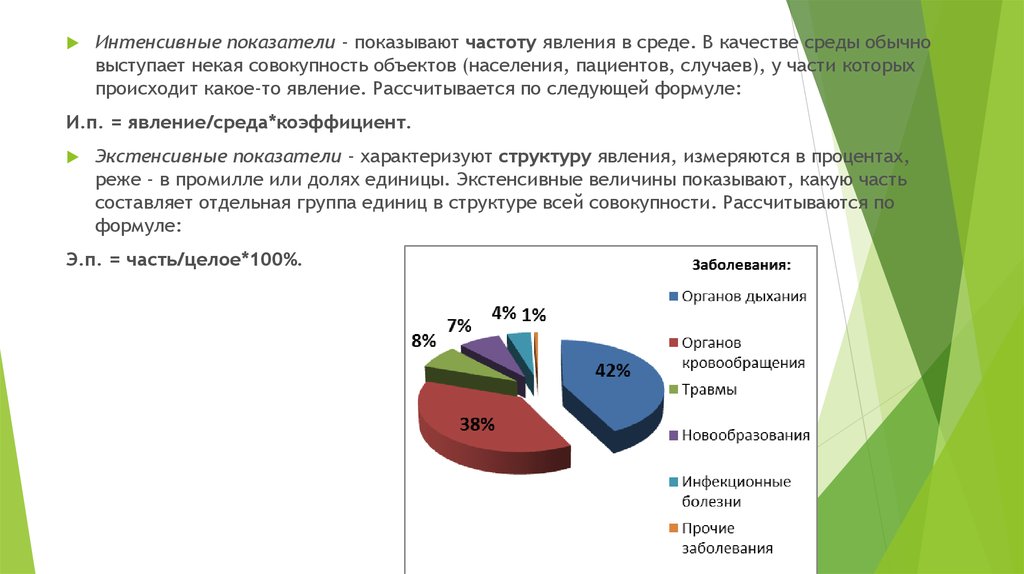
Интенсивные показатели - показывают частоту явления в среде. В качестве среды обычновыступает некая совокупность объектов (населения, пациентов, случаев), у части которых
происходит какое-то явление. Рассчитывается по следующей формуле:
И.п. = явление/среда*коэффициент.
Экстенсивные показатели - характеризуют структуру явления, измеряются в процентах,
реже - в промилле или долях единицы. Экстенсивные величины показывают, какую часть
составляет отдельная группа единиц в структуре всей совокупности. Рассчитываются по
формуле:
Э.п. = часть/целое*100%.
8. База данных
№Человек
ФИО
возраст Пол
Род занятий
Тексто Дискрет Бинарн
вая
ная
ая
Ранговая
0-ж, 1м
1- не способен работать
2- человек здоров, но не
работает
3- человек работает, но не
утруждается
4-настоящие работяги
ДИАГНОЗ
Болезнь
1-инфаркт
миокарда
2-МОИМ
3-КОИМ
4-ТМИМ
5ТМ+осложнения
Осложнени Сопутствующий
я
диагноз
бинарная Наличие-1
наличие
ос.-1
Отсутствие-0
отсутствие
ос.-0
Анализы
Rg
ВЭМ
Исход
холестер
рангов
ин
АЛТ АСТ
легкие
сердцемн
фк
ая
непре непре
непреры рывна рывна
рангов дискрет рангов
вная
я
я
ранговая ая
ная
ая
1
11- норма норма
1
2
2отклонение2- отклонение
2
3
3серьезные 3- серьезное
отклонения отклонение
3
4
качественная,ранговая
На основе базы данных мы научились пользоваться прикладным
статистическим пакетом,рассчитывать среднее значение,отклонение в
виде дисперсии,коэффициент асимметрии. научились рассчитывать
коэффициент корреляции.
4
9.
научились строить матрицу корреляции,определили как связаныпараметры нашей системы между собой
Возраст
Пол
Род
деятельн
ости
Стадия
Осложне
ния
Сопутств
ующий
диагноз
Холестер
ин
АСТ
АЛТ
Лёгкие
Сердце
Мощност
ь
нагрузки
Функц.
класс
Ранговая
1
-0,07571
1
-0,60849 0,12055
1
0,495645 0,249207 -0,40717
1
-0,16035 0,686406 0,141851 0,293241
0,251241 0,315063 -0,29435
0,71504
0,208529
0,087747
0,449578
0,403101
0,342703
0,455302
0,413099
0,212642
0,384959
-0,59437
-0,24662
-0,09762
-0,37927
-0,27111
-0,60804 0,153252 0,681647
1
0,58326
0,54237
1
0,560729
0,681331
0,603859
0,441828
0,575607
0,225851
0,498714
0,471286
0,193348
0,472848
0,487066
0,513328
0,442224
0,341069
0,302152
1
0,340779
1
0,287426 0,928102
1
0,595629 0,143389 0,004754
1
0,505008 0,488216 0,38641 0,585152
1
-0,7369 -0,04182 -0,33309 -0,53127 -0,32097 -0,21414 -0,49036 -0,47021
1
0,642516 -0,14434 -0,75689 0,554964 -0,02831 0,181902 0,577006 0,251081 0,123299 0,569202 0,543943 -0,91173
1
0,537482 0,39478 -0,45726 0,72134 0,359911 0,387709 0,609066 0,492897 0,364996 0,417054 0,425442 -0,70233 0,582137
1
10.
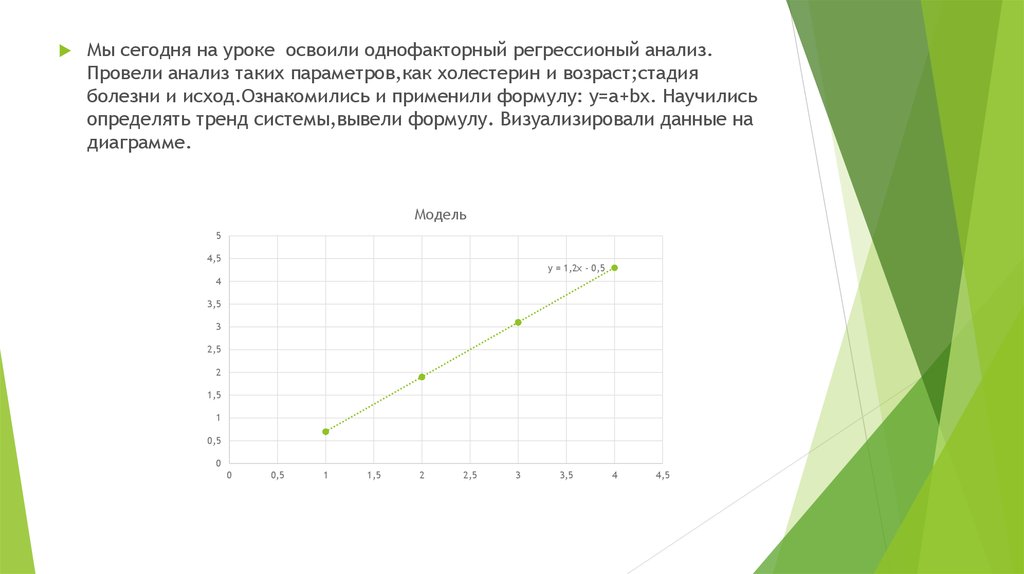
Мы сегодня на уроке освоили однофакторный регрессионый анализ.Провели анализ таких параметров,как холестерин и возраст;стадия
болезни и исход.Ознакомились и применили формулу: y=a+bx. Научились
определять тренд системы,вывели формулу. Визуализировали данные на
диаграмме.
Модель
5
4,5
y = 1,2x - 0,5
4
3,5
3
2,5
2
1,5
1
0,5
0
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
11.
освоили множественную регрессию. Множественная регрессия - этостатистическая процедура изучения зависимости, существующее между
зависимой переменной и несколькими независимыми переменными.
Моделировали зависимость между возрастом, функцией, мощностью,
холестерином и исходом .
Модель
3,5
3
2,5
2
1,5
1
0,5
0
0
-0,5
1
2
3
4
5
6
12.
Регрессия (regression) – зависимость среднего значения какой-либослучайной величины от некоторой другой величины или от нескольких
величин
Случайная величина, выполняющая роль независимой переменной в
регрессионной модели называется регрессионной переменной или (
регрессором )
Выбор функции (модели), как правило, определяется теоретическими
соображениями, а также по распределению экспериментальных значений
(x,y) на диаграмме рассеяния
Наиболее важным является случай, когда регрессия является линейной
13. Линейная регрессия
Пусть в ходе исследования были получены следующие пары наблюдений:При нанесении этих результатов на
двумерную плоскость координат, получаем
диаграмму рассеивания (облако точек).
Диаграмма рассеяния
Пульс
160
140
120
100
80
60
40
20
0
35
36
37
38
39
Температура
40
41













 medicine
medicine informatics
informatics








