Объем тела и его измерение

1.

Объем тела и его измерение
Объемом тела называется
неотрицательная величина,
определенная для каждого тела так,
что:
1) равные тела имеют равные объемы;
2) если тело составлено из нескольких
тел, попарно не имеющих общих
внутренних точек, то его объем равен
сумме объемов этих тел.

2.

За единицу объемов принимают куб,
ребро которого равно единичному отрезку
(единице длины). Объем куба со
стороной е обозначают е3.
Например, если за единицу длины принят
1 см, то за единицу объема примем куб с
ребром 1 см. Такой куб называется
кубическим сантиметром (см3).
Аналогично определяется куб. метр (м3),
куб. миллиметр (мм3) и т.д.

3.

Измерение объема состоит в сравнении
объема данного тела с объемом
единичного куба. Результатом этого
сравнения является такое число х, что
V = х е3
Число х называют численным
значением объема при выбранной
единице объема.
Число х показывает, сколько единиц
объема и частей этих единиц содержится в
данном теле.

4.

Единицы объема
1 м3 = 1000 дм3 = 1000 000 см3,
1дм3 = 1000 см3,
1 л = 1 дм3
V = 4 см3 =
= 4 ·(10-2 м)3 =
= 4 ·10-6 м3.
1 см

5.

Объем прямоугольного
параллелепипеда
с
а
V=а b с
b
Объем прямоугольного параллелепипеда
равен произведению его измерений

6.

Объем призмы
V = Sосн · h,
h
Sосн – площадь
основания,
h – высота

7.

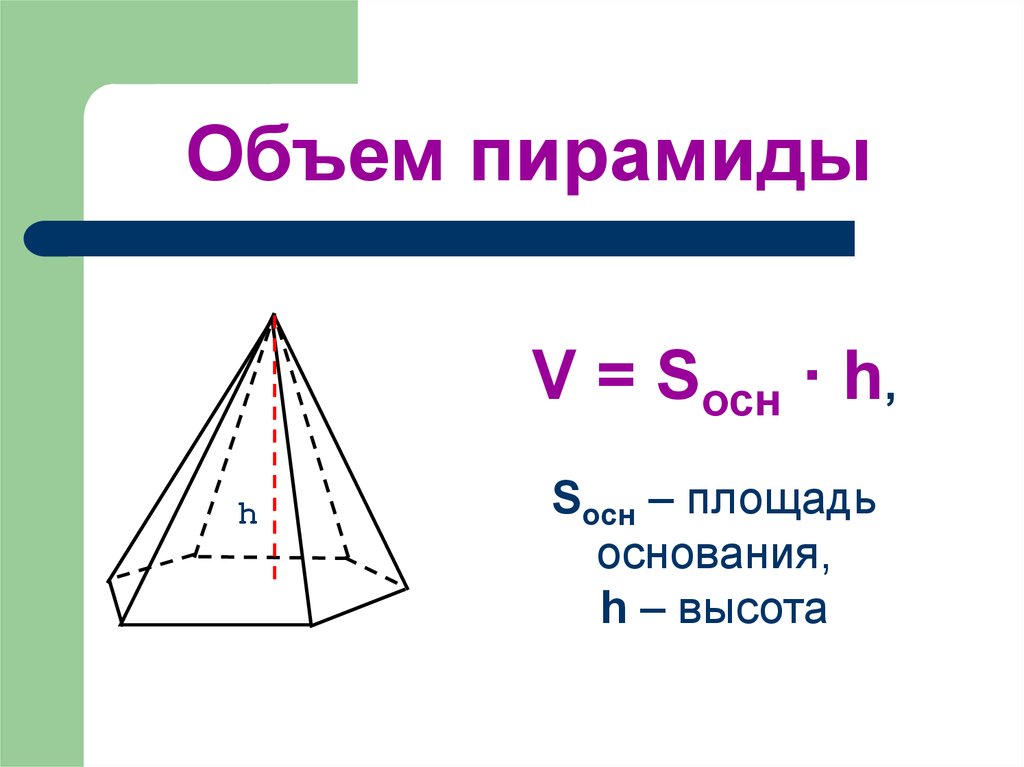
Объем пирамиды
V = Sосн · h,
h
Sосн – площадь
основания,
h – высота

8.

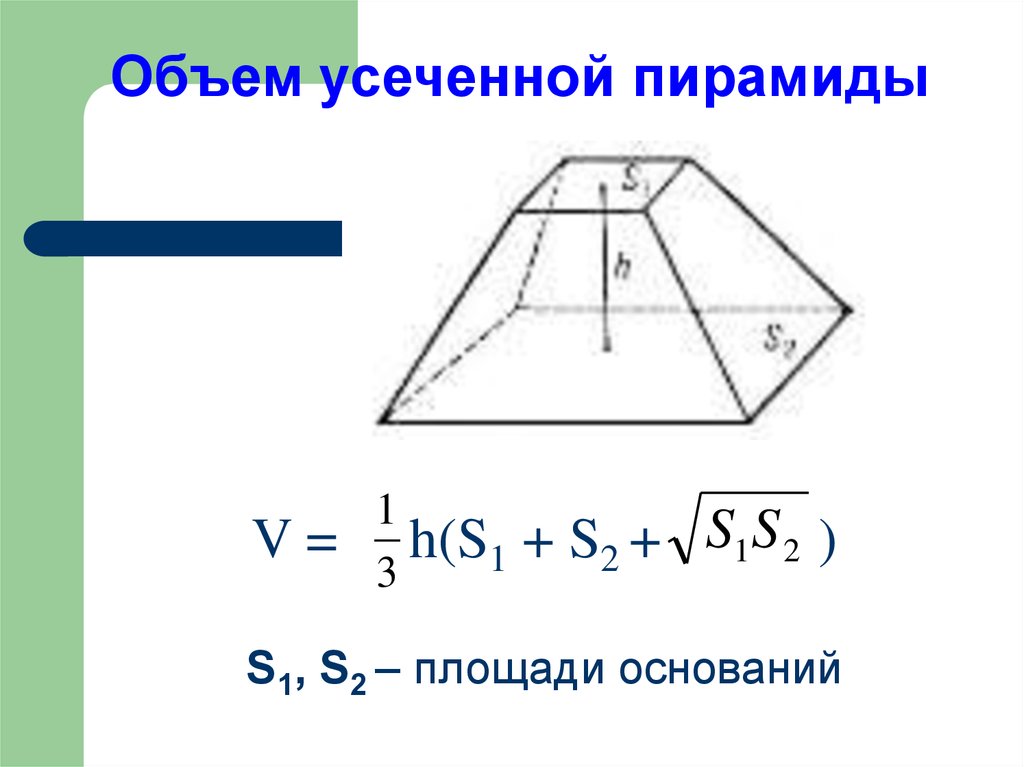
Объем усеченной пирамиды
V=
1
h(S1
3
+ S2 + S1S 2 )
S1, S2 – площади оснований

9.

Объем цилиндра
V = Sосн·h = R2·h
h
R
Sосн – площадь
основания,
h - высота,
R – радиус основания

10.

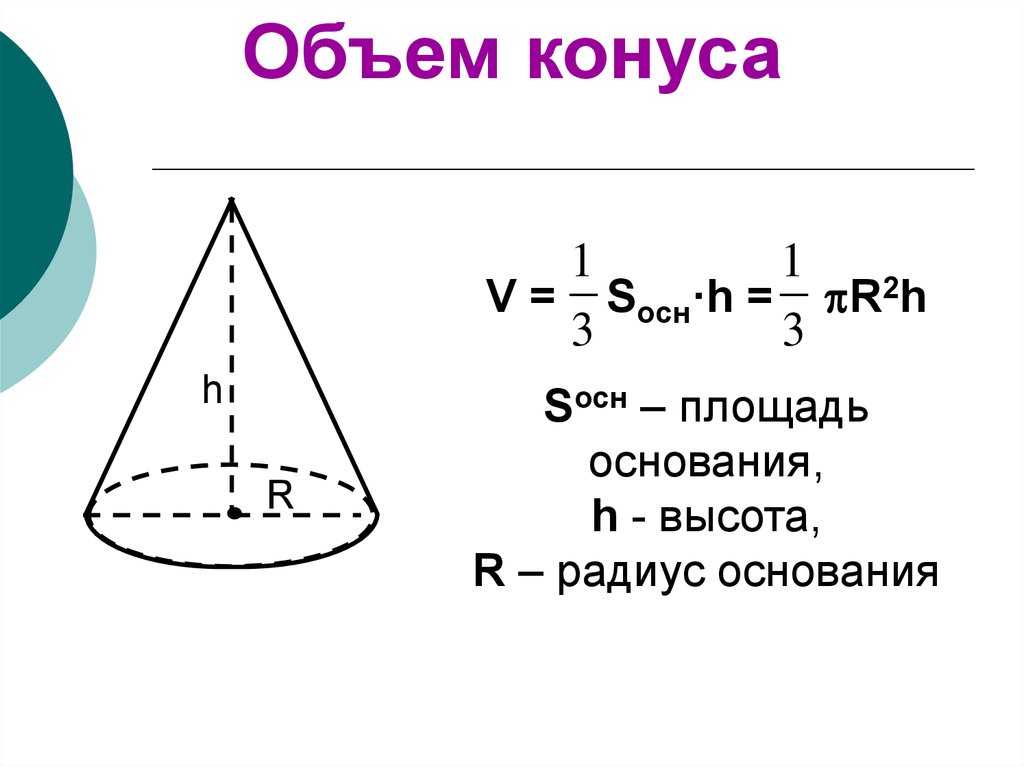
Объем конуса
1
1
V = Sосн·h = R2h
3
3
h
R
Sосн – площадь
основания,
h - высота,
R – радиус основания

11.

Объем усеченного конуса
1
V = ·h (r12+r22 + r1r2)
3
r1, r2 – радиусы оснований

12.

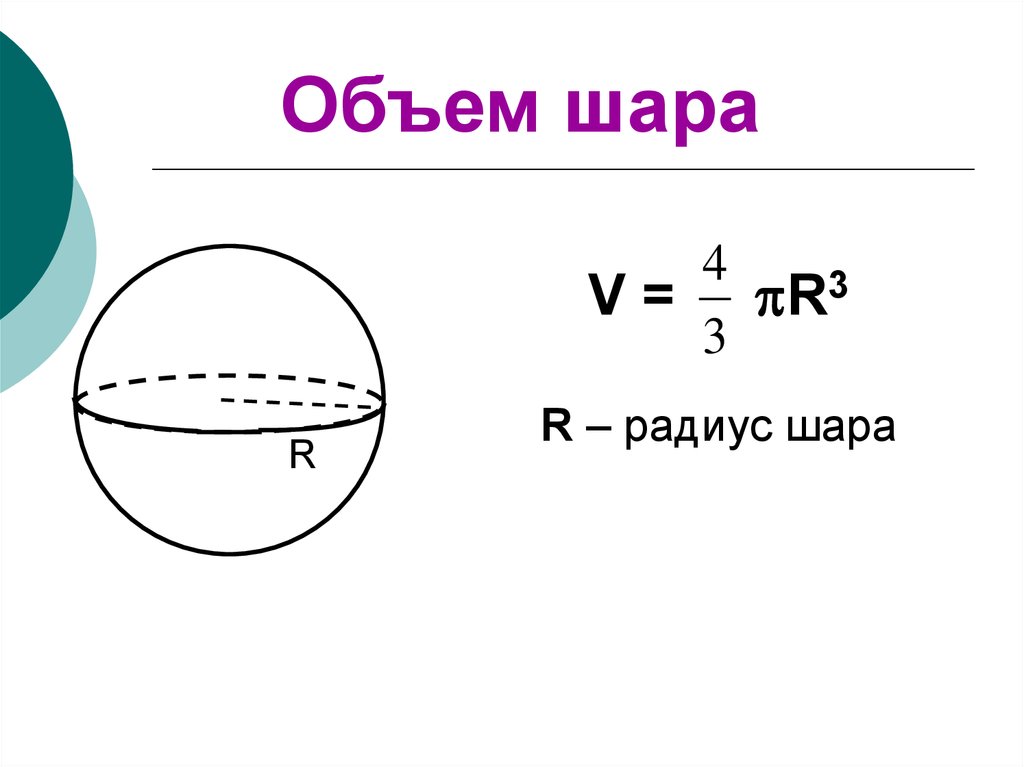
Объем шара
4
V = R3
3
R
R – радиус шара

13.

Объем шарового сегмента
h
1
V = h2(R – h)
3
R – радиус шара,
h – высота шарового
сегмента

14.

Объем шарового сектора
V=
h
R
2
3
R2h
R – радиус шара,
h – высота
шарового сегмента

15.

В начальном курсе математики
объем рассматривается как свойство
предмета занимать определенное место в
пространстве. Постепенно вводятся
следующие единицы измерения объема:
кубический сантиметр, кубический
дециметр, кубический метр, кубический
километр и кубический миллиметр.
Подготовительным этапом к измерению
объема геометрического тела являются
задания, направленные на разбиение этого
тела на единицы измерения (мерки).

16.

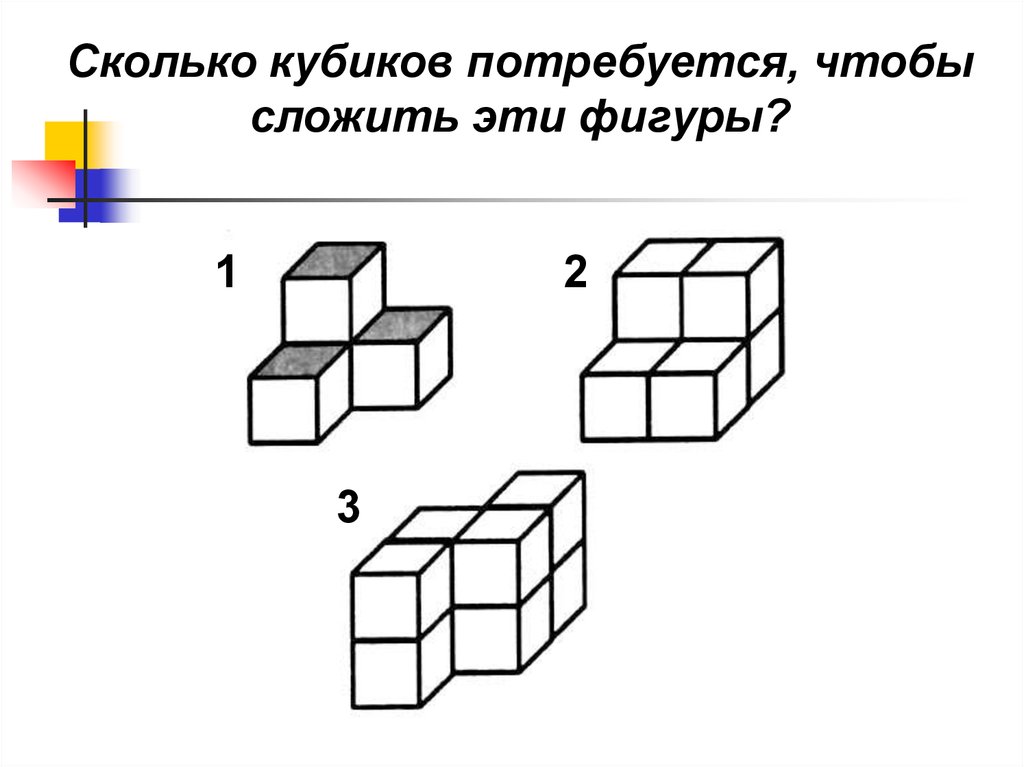
Сколько кубиков потребуется, чтобы
сложить эти фигуры?
1
2
3

17.

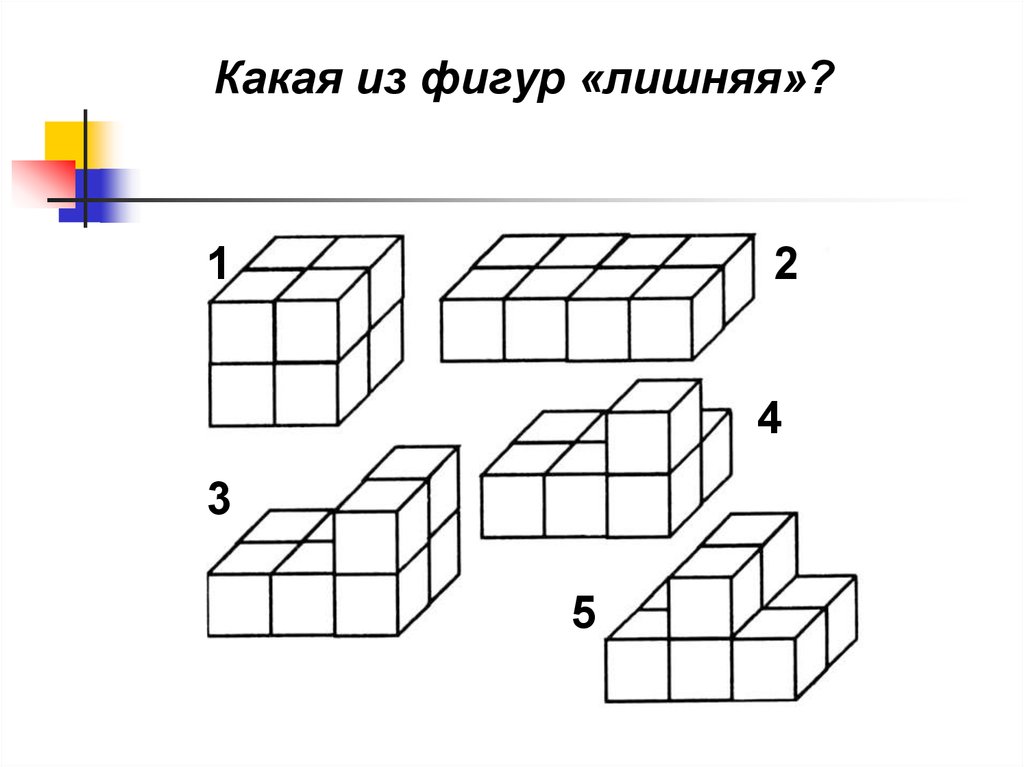
Какая из фигур «лишняя»?
1
2
4
3
5

18.

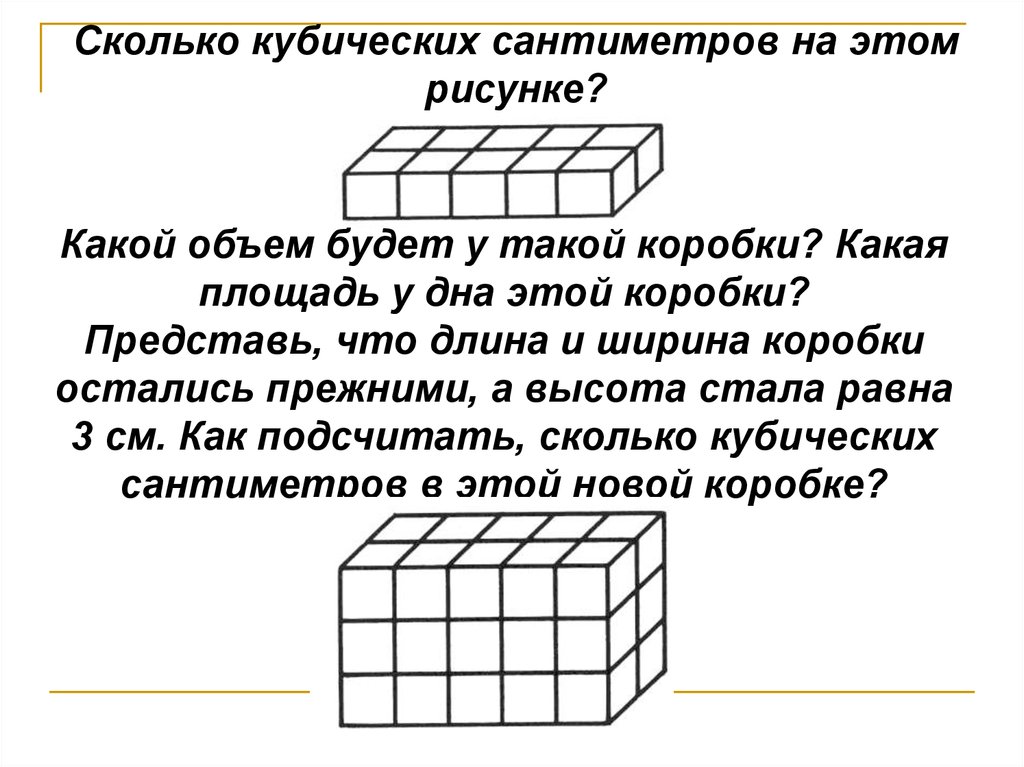
Сколько кубических сантиметров на этом
рисунке?
Какой объем будет у такой коробки? Какая
площадь у дна этой коробки?
Представь, что длина и ширина коробки
остались прежними, а высота стала равна
3 см. Как подсчитать, сколько кубических
сантиметров в этой новой коробке?