Задания ЕГЭ по информатике

1. Задания ЕГЭ. Часть 5

Задания 20. Анализ программы с
циклами и условными операторами
Задания 21. Анализ программ с циклами
и подпрограммами
Задания 22. Оператор присваивания и
ветвления. Перебор вариантов,
построение дерева
Задания 23. Логические уравнения
Задания 24 (С1). Поиск и исправление
ошибок в программеЗадания
25 (С2). Алгоритмы обработки массивов

2. 20-3

Получив на вход
число x, этот алгоритм печатает два
числа a и b.
Укажите наименьшее из таких чисел
x, при вводе которого алгоритм печатает сначала 2, а
потом 13.

3. 20-3 решение

Рассмотрим цикл, число шагов которого зависит от изменения переменной x:
while x > 0 do begin
...
x:= x div 100;
end;
Т. к. оператор div возвращает целую часть от деления, то при делении на
100 это равносильно отсечению последних двух цифр.
На каждом шаге от десятичной записи x отсекается две последних цифры
до тех пор, пока все цифры не будут отсечены, то есть x не станет равно 0.
Для того, чтобы a стало равным 2, x должно быть трёхзначным или
четырёхзначным.
Теперь рассмотрим изменение b:
while x>0 do begin
b:=b+(x mod 100);
end;
Оператор mod возвращает остаток от деления, при делении на 100 это
последние две цифры x. Разобьём 13 на два слагаемых так, чтобы можно
было составить трёхзначное число: 13 = 1 +12. Искомое число — 112.

4. 20-4

Получив на вход
число x, этот алгоритм печатает
число M. Известно,
что x > 100. Укажите
наименьшее такое
(т.е. большее 100)
число x, при вводе
которого алгоритм
печатает 26.

5. 20-4 Решение

В теле цикла числа M и L уменьшаются, пока не станут
равными. Чтобы в итоге было напечатано 26, оба
числа в какой-то момент должны быть равны 26.
Пойдем от конца к началу: на предыдущем шаге одно
число было 26, а другое 26 + 26 = 52. Еще на шаг раньше 52 + 26 = 78 и 52. До того 78 + 52 = 130 и 52. То есть
наименьшее возможное число 130. А поскольку найденное число четное, то M будет присвоено значение
52, что и приведет к необходимому результату.
Ответ: 130.

6. 21-1

Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=(x+5)*(x+3);
end;
BEGIN
a:= -5; b:=5;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)> R)then begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.

7. 21-1 решение

• 1. Алгоритм предназначен для поиска наибольшего значения функции F(t) на отрезке
от a до b.
• 2. F(x)=(x+5)(x+3) Квадратный трехчлен F(t)
положительным старшим коэффициентом
пересекает ось абсцисс в точках -5 и -3 и,
следовательно, возрастает на луче (-4; ∞).
Поэтому наибольшее значение функции достигается в точке 5 и равно F(5)=80.

8. 21-2

• Напишите в ответе
число различных
значений входной
переменной k, при
которых программа
выдаёт тот же ответ,
что и при входном
значении k = 55.
• Значение k = 55
также включается в
подсчёт различных
значений k.

9. 21-2 решение

Программа выводит минимальное , которое удовлетворяет неравенству
Найдём все подходящие k. Это те k, для которых
выполнены оба неравенства
Таким образом получаем.
Этот промежуток содержит 27 целых значений.

10. 21-3

Напишите в ответе
число различных значений входной переменной k, при которых
программа выдаёт тот
же ответ, что и при
входном значении
k = 55.
Значение k = 55 также
включается в подсчёт
различных значений k.

11. 21-3 решение

Программа находит минимальное i такое, что
выполняется неравенство
При .
Найдём все подходящие k .
Это те k, для которых выполнены оба неравенства
Таким образом получаем .
Этот промежуток содержит 18 целых значений k.

12. 21-4

При каком наименьшем значении
входной переменной k программа
выдаёт тот же
ответ, что и при
входном значении k = 64?.

13. 21-4 решение

Программа выводит максимальное I не больше 12, которое удовлетворяет неравенству .
Для для
Таким образом минимальное k — 62.

14. 21-5

Определите, какое число будет напечатано в результате выполнения следующего алгоритма:
Var a,b,t,M,R :integer;
Function F(x:integer):integer;
begin
F:=4*(x-5)*(x+3);
end;
BEGIN
a:=-20; b:=20;
M:=a; R:=F(a);
for t:=a to b do begin
if (F(t)< R)then begin
M:=t;
R:=F(t);
end;
end;
write(R);
END.

15. 21-5 решение

1. Алгоритм предназначен для поиска наименьшего значения функции F(t) на отрезке
от a до b.
2.
Квадратный трехчлен F(t) с положительным
старшим коэффициентом пересекает ось абсцисс в точках 5 и −3 и, следовательно, наименьшее значение достигается в вершине 1 и
равно F(1) = −64.

16. 22-1

• Определите значение суммы целочисленных переменных и после выполнения
фрагмента программы:

17. 22-1

• 28

18. 22-2

Определите значение переменной "с" после
выполнения следующего фрагмента программы:
x:= 8 + 2*5;
y:= (x mod 10) + 14;
x:= (y div 10) + 3;
c:= x - y;

19. 22-2 решение

• -17

20. 22-3

У исполнителя Калькулятор две команды, которым
присвоены номера:
1. прибавь 2,
2. умножь на 5.
Первая из них увеличивает число на экране на 2, вторая — увеличивает его в 5 раз.
Программа для Калькулятора — это последовательность команд.
Сколько есть программ, которые число 2 преобразуют
в число 50?

21. 22-3 решение

1. Если n не делится на 10, то тогда R(n) = R(t(n)), так как существует единственный способ получения n из t(n) — прибавлением двоек.
2. Пусть n делится на 5.
Тогда R(n) = R(n / 5) + R(n - 2)= R(n / 5) + R(n - 10) (если n > 10).
При n = 10 R(n) = 2 (два способа: прибавлением четырёх двоек или однократным умножением на 5).
Поэтому достаточно постепенно вычислить значения R(n) для всех чисел,
кратных десяти и не превосходящих 50: сначала вычисляем R(2), затем
R(10), R(20) и т. д.
Имеем:
R(2) = 1 = R(4) = R(6) = R(8),
R(10) = 2 = R(2) + R(8),
R(20) = R(4) + R(10) =1 + 2 = 3 = R(22) = R(28),
R(30) = R(6) + R(20) =1 + 3 = 4 = R(32) = R(38),
R(40) = R(8) + R(30) =1 + 4 = 5 = R(42) = R(48),
R(50) = R(10) + R(40) = 2 + 5 = 7.
Ответ: 7.

22. 22-3 решение 2

Если число на пять делится, то вариантов последней команды два: прибавь 2 и умножь на 5, тогда
.
Заполним соответствующую таблицу по приведёным формулам слева направо:
При этом ячейки, относящиеся к
числам, которые не делятся на 5,
можно в решении и опустить (за
исключением первого числа):

23. 22-4

У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 2,
2. умножь на 3.
Первая из них увеличивает число на экране на 2, вторая —
увеличивает его в 3 раза.
Программа для Утроителя — это последовательность команд.
Сколько есть программ, которые число 1 преобразуют в
число 25?
Ответ обоснуйте.

24. 22-4 решение

Верны следующие соотношения:
1. Если n не делится на 3, то тогда R(n) = R(t(n)), так как существует
единственный способ получения n из t(n) — прибавлением двоек.
2. Пусть n делится на 3.
Тогда R(n) = R(n / 3) + R(n - 2)= R(n / 3) + R(n - 6) (если n > 6).
При n = 3 R(n)) = 2 (два способа: прибавлением двоек или однократным умножением на 3).
Поэтому достаточно постепенно вычислить значения R(n) для всех
чисел, кратных 3 и не превосходящих 25: сначала вычисляем R(1),
затем R(3), R(9) и т. д.
Имеем:
R(1) = 1
R(3) = 2 = R(1) + R(1),
R(9) = R(3) + R(7) = 2 + 2 = 4 = R(11) = R(13),
R(15) = R(5) + R(13) = 2 + 2 = 4 = R(17) = R(19),
R(21) = R(7) + R(19) = 2 + 6 = 8 = R(23) = R(25).
Ответ: 8

25. 22-5

У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 3,
2. умножь на 3.
Первая из них увеличивает число на экране на 3, вторая —
увеличивает его в 3 раз.
Программа для Утроителя — это последовательность команд.
Сколько есть программ, которые число 6 преобразуют в
число 72?
Ответ обоснуйте.

26. 22-5 решение

1. Если n не делится на 9, то тогда R(n) = R(t(n)), так как существует
единственный способ получения n из t(n) — прибавлением троек.
2. Пусть n делится на 9.
Тогда R(n) = R(n / 3) + R(n - 3)= R(n / 3) + R(n - 9) (если n > 9).
При n = 9 R(n)) = 1 (один способ: прибавлением тройки).
Поэтому достаточно постепенно вычислить значения R(n) для всех
чисел, кратных 9 и не превосходящих 72: сначала вычисляем R(6),
затем R(9), R(18) и т. д.
Имеем:
R(6)=1
R(9) = 1 = R(12) = R(15),
R(18) = R(6)+R(9)=1+1=2= R(21)=R(24),
R(36) = R(12) + R(27) =1 + 3 = 4 = R(39) = R(42),
R(45) = R(15) + R(36) =1 + 4 = 5= R(48) = R(51),
R(54) = R(18) + R(45) =1 + 4 = 5= R(48) = R(51),
R(63) = R(21) + R(54) =2 + 7 =9= R(66) = R(69),
R(72) = R(24) + R(63) =2 + 9 = 11.
Ответ: 11

27. 22-4

У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь 1,
2. умножь на 3.
Первая из них увеличивает число на экране на 1, вторая — утраивает его.
Программа для Утроителя — это последовательность
команд. Сколько есть программ, которые число 4 преобразуют в число 34?
Ответ обоснуйте.

28. 22-4 решение

Тогда R(n) = R(n / 3) + R(n - 1)= R(n / 3) + R(n - 3) (если n > 3).
При n = 9 R(n)) = 1 (один способ: прибавлением тройки).
Поэтому достаточно постепенно вычислить значения R(n) для всех
чисел, кратных 3 и не превосходящих 34: сначала вычисляем R(4),
затем R(6), R(9) и т. д.
Имеем:
R(4)=1
R(6) = R(9)=1 = R(5) = R(10)= R(11),
R(12) = R(4)+R(9)=1+1=2= R(13)=R(14),
R(15) = R(5) + R(12) =1 + 2 = 3= R(16) = R(17),
R(18) = R(6) + R(15) =1 + 3 = 4= R(19) = R(20),
R(21) = R(7) + R(18) =1 + 4 = 5= R(22) = R(23),
R(24) = R(8) + R(21) =1 + 5 =6= R(25) = R(26),
R(27) = R(9) + R(24) =1 + 6 =7= R(28) = R(29),
R(30) = R(9) + R(27) =1 + 7 =8= R(31) = R(32),
R(33) = R(10) + R(30) =1 + 8 =9= R(34).
Ответ: 9

29. 22-5

У исполнителя Калькулятор две команды:
1. прибавь 2
2. умножь на 3.
Первая из них увеличивает число на экране
на 2, вторая — утраивает его. Сколько различных чисел можно получить из числа 2 с помощью программы, которая содержит ровно 3
команды?

30. 22-5 решение

С помощью одной команды из числа 2 можно получить 2 различных числа:
2 + 2 = 4,
2 * 3 = 6.
С помощью двух команд можно получить по два числа из 4 и 6:
4 + 2 = 6,
4 * 3 = 12,
6 + 2 = 8,
6 * 3 = 18.
С помощью трёх команд получаются следующие числа.
12 + 2 = 14,
12 * 3 = 36,
8 + 2 = 10,
8 * 3 = 24,
18 + 2 = 20,
18 * 3 = 54,
Число 6 даст числа 8 и 18.
Итого: 8 чисел.

31. 22-6

У исполнителя Калькулятор две команды:
1. умножь на 2
2. умножь на 3.
Первая из них умножает число на экране на 2,
вторая — утраивает его.
Сколько различных чисел можно получить из
числа 2 с помощью программы, которая содержит ровно 3 команды?

32. 22-6 решение

С помощью одной команды из числа 2 можно получить 2 различных числа:
2*2=4
2 * 3 = 6.
С помощью двух команд можно получить по два числа из 4 и 6:
4*2=8
4 * 3 = 12
6 * 2 = 12
6 * 3 = 18
Видим, что два результата совпадают, поэтому получилось 3 числа, а не 4.
С помощью трёх команд получаются следующие числа.
12 * 2 = 24
12 * 3 = 36
8 * 2 = 16
8 * 3 = 24
18 * 2 = 36
18 * 3 = 54
Числа 36 и 24 встречаются дважды, поэтому всего получаем 4 различных
числа.
Ответ: 4.

33. 23-1

Сколько существует различных наборов значений логических переменных x1, х2, хЗ, х4, х5, хб, х7, х8, которые удовлетворяют всем перечисленным ниже условиям?
(x1 —> х2) —> (хЗ—> х4) = 1
(хЗ —> х4) —> (х5 —> хб) = 1
(х5 —> хб) —> (х7 —> х8) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, х2, хЗ, х4, х5, хб, х7, х8, при которых
выполнена данная система равенств. В качестве ответа
Вам нужно указать количество таких наборов.

34. 23-1

Сделаем замену переменных:
(x1 —> х2) = y1; (хЗ—> х4) = y2; (х5 —> хб) = y3; (х7 —> х8) =
y4.
Тогда можно записать систему в виде одного уравнения:
(y1 —> y2) ∧ (y2 —> y3) ∧ (y3 —> y4) = 1.
y1
y2
y3
y4
0
0
0
0
0
0
0
1
y1
y2
y3
y4
вариант
ов
0
0
0
0
1·1·1·1
=1
0
0
1
1·1·1·3
=3
0
0
1
1
0
0
1
1
1
0
0
1
1
1
1
1
1
1·1·3·3
=9
0
1
1
1
1·3·3·3
= 27
1
1
1
1
3·3·3·3
= 81
1 + 3 + 9 + 27 + 81 = 121

35. 23-2

Сколько существует различных наборов значений логических переменных x1, х2, хЗ, х4, х5, хб, х7, х8, x9, x10 которые удовлетворяют всем перечисленным ниже условиям?
(x1 —> х2) —> (хЗ—> х4) = 1
(хЗ —> х4) —> (х5 —> хб) = 1
(х5 —> хб) —> (х7 —> х8) = 1
(х7 —> х8) —> (х9 —> х10) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, х2, хЗ, х4, х5, хб, х7, х8, x9, x10 при
которых выполнена данная система равенств. В качестве
ответа Вам нужно указать количество таких наборов.

36. 23-2

• 1 + 3 + 9 + 27 + 81 + 243 = 364.

37. 23-3

Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, x6, x7, x8 которые удовлетворяют всем перечисленным ниже условиям?
(x1≡x2)—>(x2≡x3) = 1
(x2≡x3)—>(x3≡x4) = 1
...
(x6≡x7)—>(x7≡x8) = 1
В ответе не нужно перечислять все различные наборы
значений переменных x1, x2, x3, x4, x5, x6, x7, x8 при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

38. 23-3 решение

Запишем переменные в строчку: x1x2x3x4x5x6x7x8. Импликация
ложна только в том случае, когда из истины следует ложь. Условие
не выполняется, если в ряду после пары одинаковых цифр присутствует другая цифра. Например, «11101...», что означает невыполнение второго условия.
Рассмотрим комбинации переменных, удовлетворяющие всем
условиям. Выпишем варианты, при которых все цифры чередуются, таких два: 10101010 и 01010101. Теперь для первого варианта,
начиная с конца, будем увеличивать количество повторяющихся
подряд цифр (настолько, насколько это возможно). Выпишем полученные комбинации:
«1010 1011; 1010 1111; 1011 1111; 1111 1111; 1010 1000; 1010
0000; 1000 0000; 0000 0000» таких комбинаций девять, включая
исходную. Аналогично для второго варианта:
«0101 0101; 0101 0100; 0101 0000; 0100 0000; 0000 0000; 0101
0111; 0101 1111; 0111 1111; 1111 1111» — таких комбинаций
также девять. Заметим, что комбинации 0000 0000 и 1111 1111
учтены дважды. Таким образом, получаем 9 + 9 − 2 = 16 решений.

39. 23-4

Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, x6, x7, которые удовлетворяют всем перечисленным ниже условиям?
(x1≡x2)—>(x2≡x3) = 1
(x2≡x3)—>(x3≡x4) = 1
...
(x5≡x6)—>(x6≡x7) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, x6, x7, при которых выполнена данная система равенств. В качестве ответа Вам
нужно указать количество таких наборов.

40. 23-4 решение

• 8+8-2=14

41. 23-5

Сколько существует различных наборов значений логических переменных x1, x2, ... x8, которые удовлетворяют всем перечисленным ниже условиям?
((x1 ≡ x2) ∨ (x3 ≡ x4)) ∧ (¬(x1 ≡ x2) ∨ ¬(x3 ≡ x4)) = 1
((x3 ≡ x4) ∨ (x5 ≡ x6)) ∧ (¬(x3 ≡ x4) ∨ ¬(x5 ≡ x6)) = 1
((x5 ≡ x6) ∨ (x7 ≡ x8)) ∧ (¬(x5 ≡ x6) ∨ ¬(x7 ≡ x8)) = 1
В ответе не нужно перечислять все различные наборы
значений переменных x1, x2, … x8 при которых выполнена данная система равенств. В качестве ответа Вам
нужно указать количество таких наборов.

42. 23-5 решение

• Построим древо решений первого уравнения:
Заметим, что выражение (x3 ≡ x4) в двух случаях равно 1 и в
двух случаях равно 0.
Таким образом, одно уравнение имеет восемь решений.

43. 23-5 решение (продолжение 1)

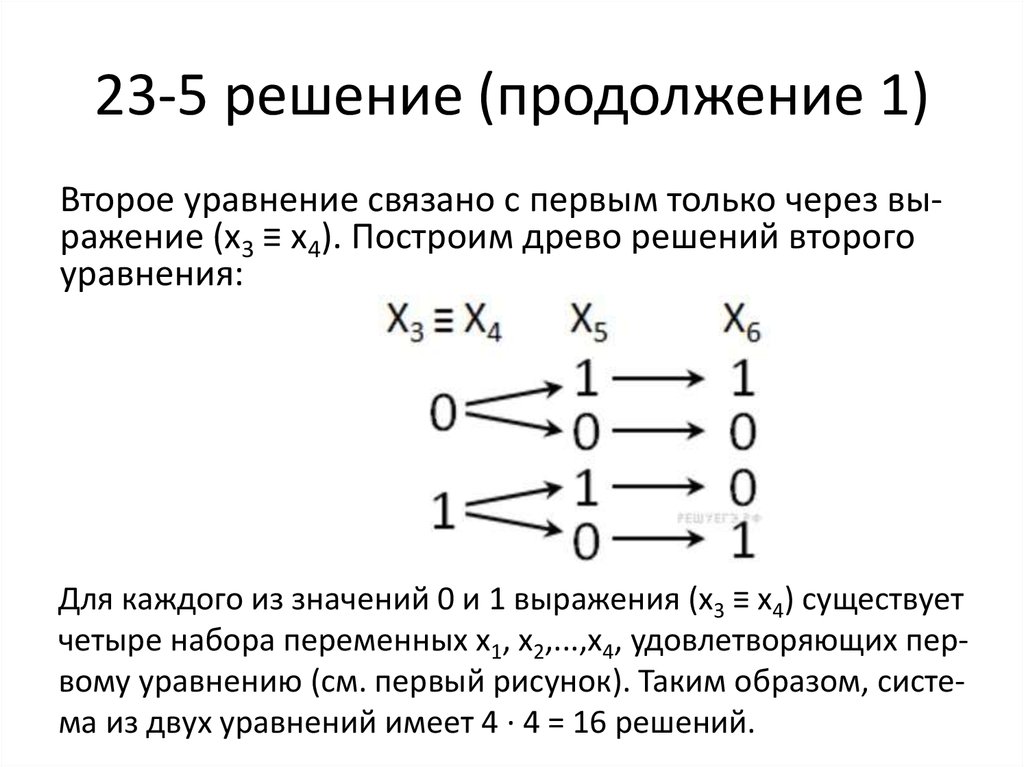
Второе уравнение связано с первым только через выражение (x3 ≡ x4). Построим древо решений второго
уравнения:
Для каждого из значений 0 и 1 выражения (x3 ≡ x4) существует
четыре набора переменных x1, x2,...,x4, удовлетворяющих первому уравнению (см. первый рисунок). Таким образом, система из двух уравнений имеет 4 · 4 = 16 решений.

44. 23-5 решение (продолжение 2)

Третье уравнение связано со вторым только
через выражение (x5 ≡ x6). Построим древо решений третьего уравнения:
Для каждого из значений 0 и 1 выражения (x5 ≡ x6) существует
2 · 4 = 8 наборов переменных x1, x2,...,x6, удовлетворяющих первому уравнению (см. первый и второй рисунок). Таким образом, система из трёх уравнений имеет 8 · 4 = 32 решения.